华师大版七年级下册(新)第9章《9.1.1 认识三角形的边》课件(27张PPT)
文档属性
| 名称 | 华师大版七年级下册(新)第9章《9.1.1 认识三角形的边》课件(27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-11 07:35:34 | ||
图片预览




文档简介
课件27张PPT。9.1 三角形
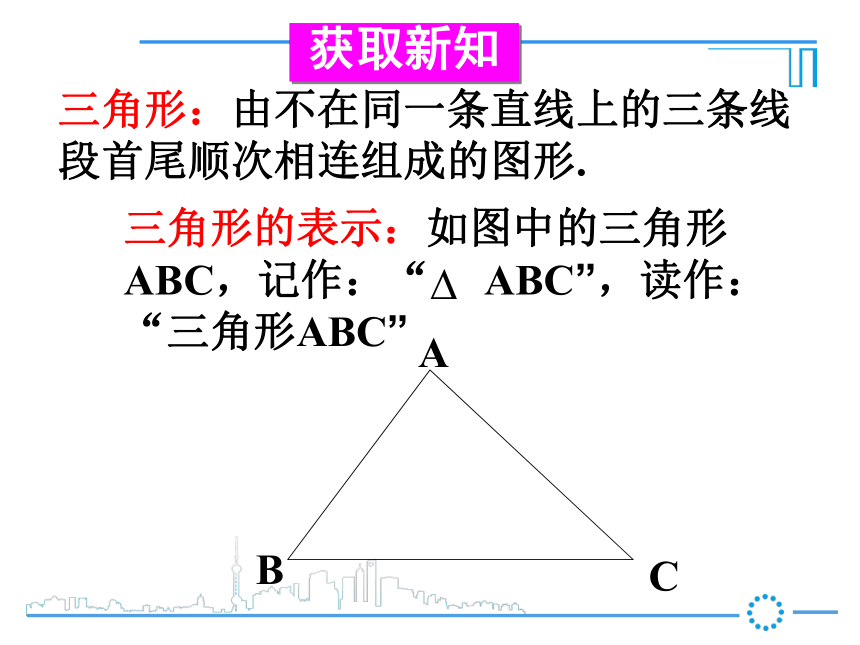
第1课时 三角形的概念华东师大·七年级下册第九章 三角形情境导入生活中的三角形!三角形:由不在同一条直线上的三条线 段首尾顺次相连组成的图形.三角形的表示:如图中的三角形ABC,记作:“ ABC”,读作:“三角形ABC” 获取新知顶点内角边三个顶点是:A、B、C三个内角是 : A 、 B、 C 如图:在 ABC中
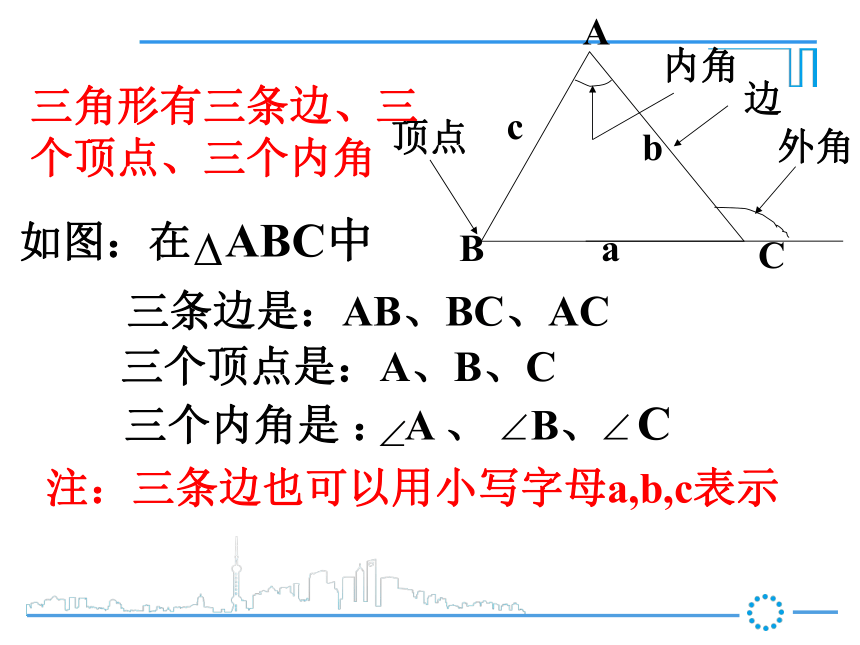
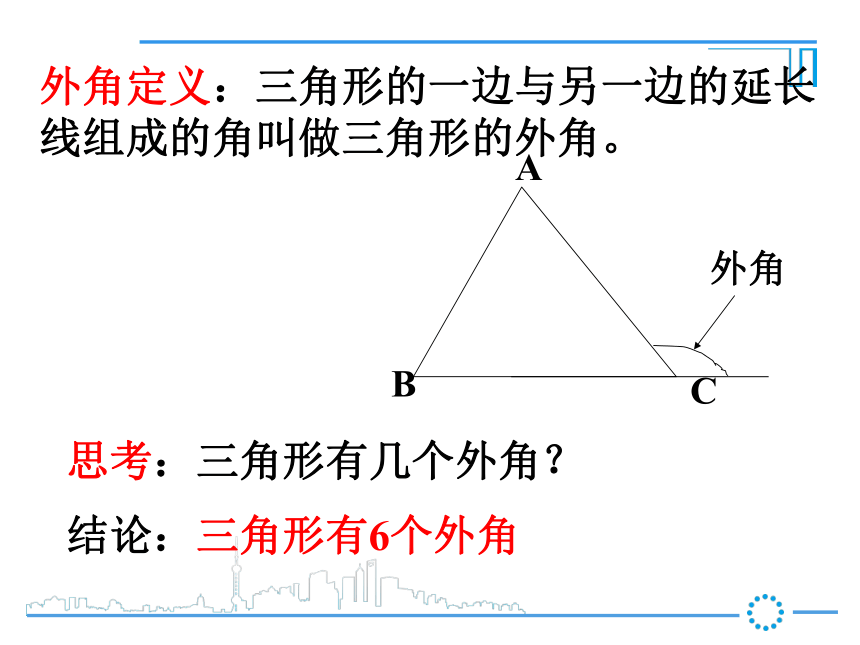
三条边是:AB、BC、AC注:三条边也可以用小写字母a,b,c表示 三角形有三条边、三个顶点、三个内角外角外角外角定义:三角形的一边与另一边的延长线组成的角叫做三角形的外角。思考:三角形有几个外角?结论:三角形有6个外角 等腰三角形:两条边相等的三角形
等边三角形:三条边相等的三角形,(又叫正三角形)三角形按边分类:判断:
1.有两边相等的三角形叫做等腰三角形. ( )
2.只有两边相等的三角形叫做等腰三角形. ( )
3.等边三角形是等腰三角形.( )√×√随堂演练1.三角形的顶点、边、内角及外角 2.三边的数量关系 .3.三角形按边的分类 .课堂小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业第2课时 三角形的高、角平分线和中线华东师大·七年级下册A从三角形的一个顶点BC向它的对边所在直线作垂线,顶点和垂足之间的线段 叫做三角形这边的高,简称三角形的高。如图, 线段AD是BC边上的高. 任意画一个锐角△ABC,和垂足的字母.请你画出BC边上的高.推进新课锐角三角形的三条高ABCDEF∵AD是△ABC的高∴AD⊥BC,
∠ADC=∠ADB=90°(高的定义)锐角三角形的三条高相交于同一点.锐角三角形的三条高都在三角形的内部。锐角三角形的三条高是 在三角形的内部还是外部?直角三角形的三条高ABC直角边BC边上的高是__________; AB直角边AB边上的高是 ;CBD斜边AC边上的高是______________. BD●直角三角形的三条高
交于直角顶点.做BC边上的高, BC边不够长怎么办?钝角三角形的三条高ABCDFE把CB延长BC边上的高是在三角形的内部还是外部?AB边上的高呢?外部钝角三角形的三条高ABCDF钝角三角形的三条高交于一点吗?钝 角三角形的三条高不相交于一点E钝角三角形的三条高所在直线交于一点,交点在三角形外三角形的角平分线叫做三角形的角平分线。ABCD∵AD是 △ ABC的角平分线●●在三角形中,一个角的角平分线与这个角的对边相交,这个角的顶点与交点之间的线段,(角平分线的定义)ACBFEDO∵BE是△ABC的角平分线∴ =_____ = _____∴∠ACB=2______=2______∠ABE ∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF 三角形的角平分线与角的平分线有什么区别?思考三角形的角平分线是一条线段 , 角的平分线是一条射线.角平分线的理解三角形的角平分线每人准备锐角三角形、钝角三角形和直角三角形纸片各一个。
(1) 分别画出这三个三角形的三条角平分线吗?(2) 在每个三角形中,这三条角平分线之间有怎样的位置关系?三角形的三条角平分线交于同一点.三角形的中线在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边的中线.D∵AD是△ ABC的中线●●EFO(中线的定义)三角形的三条中线(2) 试画钝角三角形和直角三角形的三条中线你发现了什么?三角形的三条中线相交于一点,交点在三角形的内部.
我们把这三条中线的交点叫做三角形的重心.如图,O是△ABC的重心.例1、点D是△ABC的BC边上的一点。∵BD=CD,
∴线段AD是△ABC的___ ∵∠BAD=∠CAD,
∴线段AD是△ABC的_____∵∠ADC=90°,
∴线段AD是△ABC的___中线角平分线高典例解析 例2、如图,AD、AM、AH分别是△ABC的角平分线、中线、高。(1)∵AD是△ABC的角平分线,
∴∠ =∠ = ∠ 。 (2) ∵AM是△ABC的中线,
∴ = = 。(3)∵AH是△ABC的高,
∴∠ =∠ =90°BADDACBACBMCMBCAHCAHB例3、如图,BD=DE=EF=FC。AD是△____的中线,____是△AEC的中线,AE是△____和△_____的中线。ABEAFABCADF1.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形B2.在下图中,如果AE=ED=DC,则BE、BD分别是 的中线,
图中有没有面积相等的三角形?△ABD 、△BCE随堂演练1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业劳动教养了身体,学习教养了心灵。 —— 史密斯
第1课时 三角形的概念华东师大·七年级下册第九章 三角形情境导入生活中的三角形!三角形:由不在同一条直线上的三条线 段首尾顺次相连组成的图形.三角形的表示:如图中的三角形ABC,记作:“ ABC”,读作:“三角形ABC” 获取新知顶点内角边三个顶点是:A、B、C三个内角是 : A 、 B、 C 如图:在 ABC中
三条边是:AB、BC、AC注:三条边也可以用小写字母a,b,c表示 三角形有三条边、三个顶点、三个内角外角外角外角定义:三角形的一边与另一边的延长线组成的角叫做三角形的外角。思考:三角形有几个外角?结论:三角形有6个外角 等腰三角形:两条边相等的三角形
等边三角形:三条边相等的三角形,(又叫正三角形)三角形按边分类:判断:
1.有两边相等的三角形叫做等腰三角形. ( )
2.只有两边相等的三角形叫做等腰三角形. ( )
3.等边三角形是等腰三角形.( )√×√随堂演练1.三角形的顶点、边、内角及外角 2.三边的数量关系 .3.三角形按边的分类 .课堂小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业第2课时 三角形的高、角平分线和中线华东师大·七年级下册A从三角形的一个顶点BC向它的对边所在直线作垂线,顶点和垂足之间的线段 叫做三角形这边的高,简称三角形的高。如图, 线段AD是BC边上的高. 任意画一个锐角△ABC,和垂足的字母.请你画出BC边上的高.推进新课锐角三角形的三条高ABCDEF∵AD是△ABC的高∴AD⊥BC,
∠ADC=∠ADB=90°(高的定义)锐角三角形的三条高相交于同一点.锐角三角形的三条高都在三角形的内部。锐角三角形的三条高是 在三角形的内部还是外部?直角三角形的三条高ABC直角边BC边上的高是__________; AB直角边AB边上的高是 ;CBD斜边AC边上的高是______________. BD●直角三角形的三条高
交于直角顶点.做BC边上的高, BC边不够长怎么办?钝角三角形的三条高ABCDFE把CB延长BC边上的高是在三角形的内部还是外部?AB边上的高呢?外部钝角三角形的三条高ABCDF钝角三角形的三条高交于一点吗?钝 角三角形的三条高不相交于一点E钝角三角形的三条高所在直线交于一点,交点在三角形外三角形的角平分线叫做三角形的角平分线。ABCD∵AD是 △ ABC的角平分线●●在三角形中,一个角的角平分线与这个角的对边相交,这个角的顶点与交点之间的线段,(角平分线的定义)ACBFEDO∵BE是△ABC的角平分线∴ =_____ = _____∴∠ACB=2______=2______∠ABE ∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF 三角形的角平分线与角的平分线有什么区别?思考三角形的角平分线是一条线段 , 角的平分线是一条射线.角平分线的理解三角形的角平分线每人准备锐角三角形、钝角三角形和直角三角形纸片各一个。
(1) 分别画出这三个三角形的三条角平分线吗?(2) 在每个三角形中,这三条角平分线之间有怎样的位置关系?三角形的三条角平分线交于同一点.三角形的中线在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边的中线.D∵AD是△ ABC的中线●●EFO(中线的定义)三角形的三条中线(2) 试画钝角三角形和直角三角形的三条中线你发现了什么?三角形的三条中线相交于一点,交点在三角形的内部.
我们把这三条中线的交点叫做三角形的重心.如图,O是△ABC的重心.例1、点D是△ABC的BC边上的一点。∵BD=CD,
∴线段AD是△ABC的___ ∵∠BAD=∠CAD,
∴线段AD是△ABC的_____∵∠ADC=90°,
∴线段AD是△ABC的___中线角平分线高典例解析 例2、如图,AD、AM、AH分别是△ABC的角平分线、中线、高。(1)∵AD是△ABC的角平分线,
∴∠ =∠ = ∠ 。 (2) ∵AM是△ABC的中线,
∴ = = 。(3)∵AH是△ABC的高,
∴∠ =∠ =90°BADDACBACBMCMBCAHCAHB例3、如图,BD=DE=EF=FC。AD是△____的中线,____是△AEC的中线,AE是△____和△_____的中线。ABEAFABCADF1.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形B2.在下图中,如果AE=ED=DC,则BE、BD分别是 的中线,
图中有没有面积相等的三角形?△ABD 、△BCE随堂演练1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业劳动教养了身体,学习教养了心灵。 —— 史密斯
