沪科版数学2024-2025学年数学七年级上册 第四章 几何图形初步 综合测试卷(含答案)
文档属性
| 名称 | 沪科版数学2024-2025学年数学七年级上册 第四章 几何图形初步 综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 173.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 15:38:24 | ||
图片预览

文档简介
第四章综合测试卷
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题5分,满分50分)
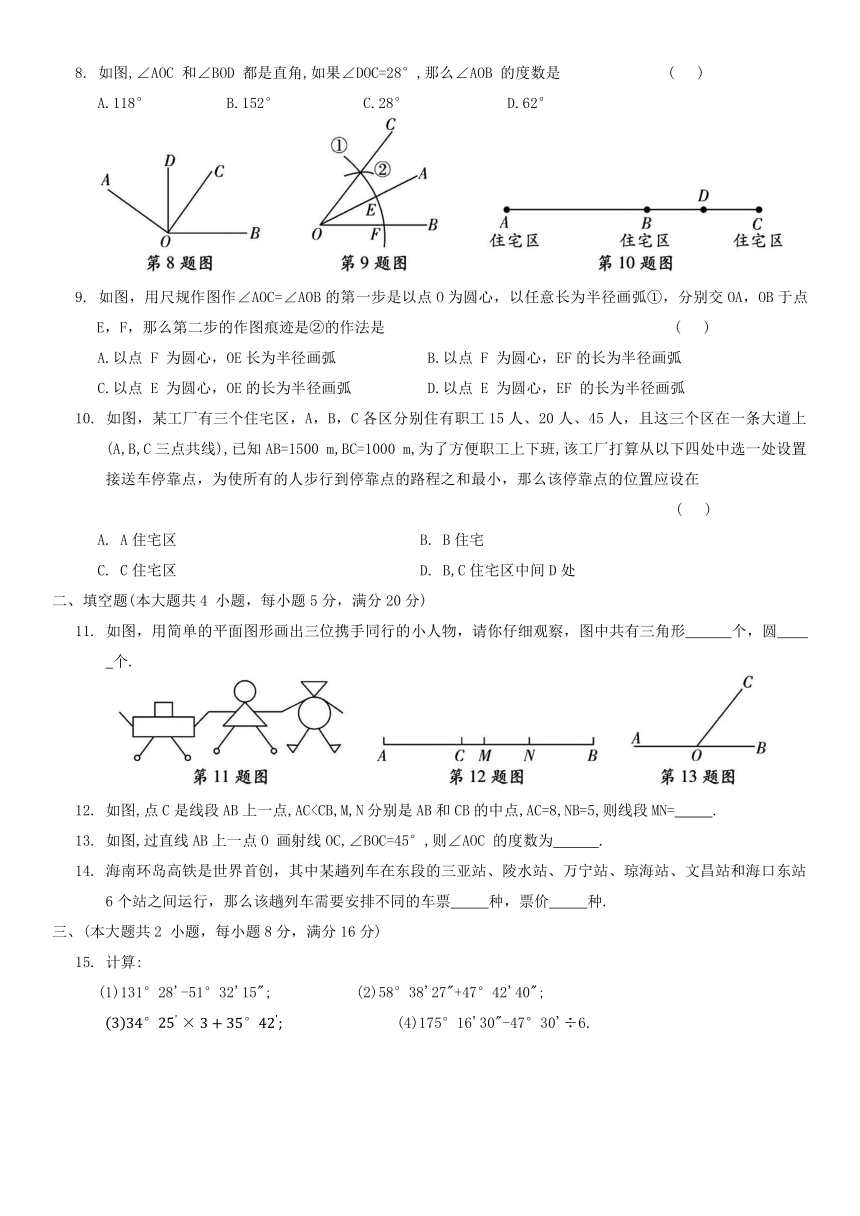
1. 如图所示的立体图形中,不是柱体的是 ( )
2. 如图,点C,D在线段AB 上.则下列表述或结论错误的是 ( )
A.图中共有线段12条 B. AC=AD+DB-BC
C. AD=AB+CD-BC D.若AC=BD,则AD=BC
3. 图中下列从A 到B的各条路线中最短的路线是 ( )
A. A→C→G→E→B B. A→C→E→B
C. A→D→G→E→B D. A→F→E→B
4. 如图,已知线段AB=6cm,在线段AB的延长线上有一点C,且BC=4cm,若点M为AB中点,那么 MC 的长度为 ( )
A.5cm B.6cm C.7 cm D.无法确定
5. 已知∠A=115°,∠B 是∠A 的补角,则∠B 的余角的度数是 ( )
A.65° B.115° C.15° D.25°
6. 体育课上,小聪、小明、小智、小慧分别在点O处进行了一次铅球试投,铅球分别落在图中的点A,B,C,D处,则他们四人中,成绩最好的是 ( )
A.小聪 B.小明 C.小智 D.小慧
7. 下列日常现象:
①用两根钉子就可以把一根木条固定在墙上;
②把弯曲的公路改直,就能够缩短路程;
③利用圆规可以比较两条线段的大小;
④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙.
其中,可以用"两点确定一条直线"来解释的现象是 ( )
A.①④ B.②③ C.①②④ D.①③④
8. 如图,∠AOC 和∠BOD 都是直角,如果∠DOC=28°,那么∠AOB 的度数是 ( )
A.118° B.152° C.28° D.62°
9. 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA,OB于点E,F,那么第二步的作图痕迹是②的作法是 ( )
A.以点 F 为圆心,OE长为半径画弧 B.以点 F 为圆心,EF的长为半径画弧
C.以点 E 为圆心,OE的长为半径画弧 D.以点 E 为圆心,EF 的长为半径画弧
10. 如图,某工厂有三个住宅区,A,B,C各区分别住有职工15人、20人、45人,且这三个区在一条大道上(A,B,C三点共线),已知AB=1500 m,BC=1000 m,为了方便职工上下班,该工厂打算从以下四处中选一处设置接送车停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在 ( )
A. A住宅区 B. B住宅
C. C住宅区 D. B,C住宅区中间D处
二、填空题(本大题共4 小题,每小题5分,满分20分)
11. 如图,用简单的平面图形画出三位携手同行的小人物,请你仔细观察,图中共有三角形 个,圆 个.
12. 如图,点C是线段AB上一点,AC13. 如图,过直线AB上一点O 画射线OC,∠BOC=45°,则∠AOC 的度数为 .
14. 海南环岛高铁是世界首创,其中某趟列车在东段的三亚站、陵水站、万宁站、琼海站、文昌站和海口东站6个站之间运行,那么该趟列车需要安排不同的车票 种,票价 种.
三、(本大题共2 小题,每小题8分,满分16分)
15. 计算:
(1)131°28'-51°32'15"; (2)58°38'27"+47°42'40";
(4)175°16'30"-47°30'÷6.
16. 如图,已知点A,B,C,D,根据下列语句画图.(不写作图过程)
作射线AB、直线AC,连接AD 并延长线段AD.
四、(本大题共2小题,每小题8分,满分16分)
17. 如图,已知线段a和线段AB.
(1)延长线段AB到C,使BC=a(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AB=5,BC=3,点O是线段AC的中点,求线段OB的长.
18. 如图,两个直角三角形的直角顶点重合,∠AOC=40°,求∠BOD 的度数.
结合图形,完成填空:
解法1:
因为∠AOC+∠COB=90°,∠AOC=40°,所以.
因为 所以
所以
解法2:
因为
所以∠AOC= .②
因为∠AOC=40°,所以∠BOD= °.
在上面①到②的推导过程中,理由依据是: .
五、(本题满分10分)
19. 如图,已知OE平分∠AOC,OD平分∠BOC,若 求 的度数.
六、(本题满分12分)
20. 如图,已知线段AB上顺次有三个点 C,D,E,它们把线段AB分成2:3:4:5四部分,且 56 cm.
(1)求线段AE 的长.
(2)若M,N分别是DE,EB的中点,求线段MN的长度.
七、(本题满分12分)
21. 如图,OD平分. OE 平分 若
(1)请求出. 及其补角的度数.
(2)请求出 和 的度数,并判断. 与 是否互补,并说明理由.
八、(本题满分14分)
22. (1)如图(a),将一副三角尺( )的直角顶点 C 叠放在一起,边CD 与 BE相交.
①若 则 若 则
②猜想 与 的数量关系.直接写出答案,无需证明.
(2)如图(b),若两个相同的三角尺( 锐角的顶点A 重合在一起,边CD与AE相交,则 与 有何数量关系 请说明理由.
第四章综合测试卷
1. D 2. A 3. D 4. C 5. D 6. C 7. A 8. B 9. D10. C 11. 4 6 12. 4 13. 135° 14. 30 15
15. 解:(1)原式=79°55'45".
(2)原式
(3)原式=103°15'+35°42'=138°57'.
(4)原式=175°16'30"-7°55'=167°20'30".
16. 解:如图所示:
17. 解:(1)如图:
(2)因为AB=5,BC=3,
所以AC=8,
因为点O 是线段AC的中点,
所以AO=CO=4,
所以BO=AB-AO=5-4=1,所以OB长为1.
18. 解:解法1:因为∠AOC+∠COB=90°,∠AOC=40°,所以∠COB=50°.
因为∠COB+∠BOD=90°,所以∠BOD=90°-∠COB,所以∠BOD=40°.
解法2:因为∠AOC+∠COB=90°,∠COB+∠BOD=90°,①所以∠AOC=∠BOD.② 因为∠AOC=40°,所以∠BOD=40°.
在上面①到②的推导过程中,理由依据是:同角的余角相等.
故答案为:50,90,90,40;90,90,∠BOD,40,同角的余角相等.
19. 解:因为∠AOC = 120°,OE 平分∠AOC,所以∠EOC =∠AOE=60°.又因为 OD 平分∠BOC,∠BOC =30°,所以 所以∠DOE = ∠EOC-∠COD=60°-15°=45°.
20. 解:(1)设AC=2x cm,则CD,DE,EB的长度分别为3x cm,4x cm,5x cm,由题意得:2x+3x+4x+5x=56,解得x=4,则AC,CD,DE,EB 的长度分别分为8cm ,12 cm,16 cm,20cm,所以AE=AC+CD+DE=36 cm.
(2)因为M是DE的中点,所以 因为N是EB的中点,所以 所以 MN = ME +EN=18 cm.
21. 解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,其补角的度数为180°-∠AOB=180°-120°=60°.
∠DOE 与∠AOB 互补.
理由如下:因为∠DOC=35°,∠COE=∠AOE=25°,所以∠DOE=∠DOC+∠COE=60°,所以∠DOE+∠AOB=60°+120°=180°,所以∠DOE与∠AOB互补.
22. 解:(1)①若∠DCE=25°,因为∠ACD=90°,∠DCE=25°,所以∠ACE =90°-25°=65°,因为∠BCE = 90°,所以∠ACB = ∠ACE + ∠BCE =65°+90°= 155°;若∠ACB =130°,因为∠BCE=90°,所以∠ACE =130°-90°=40°,因为∠ACD=90°,所以∠DCE=90°-40°=50°,故答案为:155°;50°.
②∠ACB+∠DCE=180°,
理由如下:因为∠ACB=∠ACD+∠BCD=90°+∠BCD,所以∠ACB+∠DCE=90°+∠BCD+∠DCE,=90°+∠BCE=180°.
(2)∠DAB+∠CAE=120°,理由如下:因为∠DAB =∠DAC+∠CAB=60°+∠CAB,
所以∠DAB+∠CAE=60°+∠CAB +∠CAE=60°+∠EAB=120°.
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题5分,满分50分)
1. 如图所示的立体图形中,不是柱体的是 ( )
2. 如图,点C,D在线段AB 上.则下列表述或结论错误的是 ( )
A.图中共有线段12条 B. AC=AD+DB-BC
C. AD=AB+CD-BC D.若AC=BD,则AD=BC
3. 图中下列从A 到B的各条路线中最短的路线是 ( )
A. A→C→G→E→B B. A→C→E→B
C. A→D→G→E→B D. A→F→E→B
4. 如图,已知线段AB=6cm,在线段AB的延长线上有一点C,且BC=4cm,若点M为AB中点,那么 MC 的长度为 ( )
A.5cm B.6cm C.7 cm D.无法确定
5. 已知∠A=115°,∠B 是∠A 的补角,则∠B 的余角的度数是 ( )
A.65° B.115° C.15° D.25°
6. 体育课上,小聪、小明、小智、小慧分别在点O处进行了一次铅球试投,铅球分别落在图中的点A,B,C,D处,则他们四人中,成绩最好的是 ( )
A.小聪 B.小明 C.小智 D.小慧
7. 下列日常现象:
①用两根钉子就可以把一根木条固定在墙上;
②把弯曲的公路改直,就能够缩短路程;
③利用圆规可以比较两条线段的大小;
④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙.
其中,可以用"两点确定一条直线"来解释的现象是 ( )
A.①④ B.②③ C.①②④ D.①③④
8. 如图,∠AOC 和∠BOD 都是直角,如果∠DOC=28°,那么∠AOB 的度数是 ( )
A.118° B.152° C.28° D.62°
9. 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA,OB于点E,F,那么第二步的作图痕迹是②的作法是 ( )
A.以点 F 为圆心,OE长为半径画弧 B.以点 F 为圆心,EF的长为半径画弧
C.以点 E 为圆心,OE的长为半径画弧 D.以点 E 为圆心,EF 的长为半径画弧
10. 如图,某工厂有三个住宅区,A,B,C各区分别住有职工15人、20人、45人,且这三个区在一条大道上(A,B,C三点共线),已知AB=1500 m,BC=1000 m,为了方便职工上下班,该工厂打算从以下四处中选一处设置接送车停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在 ( )
A. A住宅区 B. B住宅
C. C住宅区 D. B,C住宅区中间D处
二、填空题(本大题共4 小题,每小题5分,满分20分)
11. 如图,用简单的平面图形画出三位携手同行的小人物,请你仔细观察,图中共有三角形 个,圆 个.
12. 如图,点C是线段AB上一点,AC
14. 海南环岛高铁是世界首创,其中某趟列车在东段的三亚站、陵水站、万宁站、琼海站、文昌站和海口东站6个站之间运行,那么该趟列车需要安排不同的车票 种,票价 种.
三、(本大题共2 小题,每小题8分,满分16分)
15. 计算:
(1)131°28'-51°32'15"; (2)58°38'27"+47°42'40";
(4)175°16'30"-47°30'÷6.
16. 如图,已知点A,B,C,D,根据下列语句画图.(不写作图过程)
作射线AB、直线AC,连接AD 并延长线段AD.
四、(本大题共2小题,每小题8分,满分16分)
17. 如图,已知线段a和线段AB.
(1)延长线段AB到C,使BC=a(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AB=5,BC=3,点O是线段AC的中点,求线段OB的长.
18. 如图,两个直角三角形的直角顶点重合,∠AOC=40°,求∠BOD 的度数.
结合图形,完成填空:
解法1:
因为∠AOC+∠COB=90°,∠AOC=40°,所以.
因为 所以
所以
解法2:
因为
所以∠AOC= .②
因为∠AOC=40°,所以∠BOD= °.
在上面①到②的推导过程中,理由依据是: .
五、(本题满分10分)
19. 如图,已知OE平分∠AOC,OD平分∠BOC,若 求 的度数.
六、(本题满分12分)
20. 如图,已知线段AB上顺次有三个点 C,D,E,它们把线段AB分成2:3:4:5四部分,且 56 cm.
(1)求线段AE 的长.
(2)若M,N分别是DE,EB的中点,求线段MN的长度.
七、(本题满分12分)
21. 如图,OD平分. OE 平分 若
(1)请求出. 及其补角的度数.
(2)请求出 和 的度数,并判断. 与 是否互补,并说明理由.
八、(本题满分14分)
22. (1)如图(a),将一副三角尺( )的直角顶点 C 叠放在一起,边CD 与 BE相交.
①若 则 若 则
②猜想 与 的数量关系.直接写出答案,无需证明.
(2)如图(b),若两个相同的三角尺( 锐角的顶点A 重合在一起,边CD与AE相交,则 与 有何数量关系 请说明理由.
第四章综合测试卷
1. D 2. A 3. D 4. C 5. D 6. C 7. A 8. B 9. D10. C 11. 4 6 12. 4 13. 135° 14. 30 15
15. 解:(1)原式=79°55'45".
(2)原式
(3)原式=103°15'+35°42'=138°57'.
(4)原式=175°16'30"-7°55'=167°20'30".
16. 解:如图所示:
17. 解:(1)如图:
(2)因为AB=5,BC=3,
所以AC=8,
因为点O 是线段AC的中点,
所以AO=CO=4,
所以BO=AB-AO=5-4=1,所以OB长为1.
18. 解:解法1:因为∠AOC+∠COB=90°,∠AOC=40°,所以∠COB=50°.
因为∠COB+∠BOD=90°,所以∠BOD=90°-∠COB,所以∠BOD=40°.
解法2:因为∠AOC+∠COB=90°,∠COB+∠BOD=90°,①所以∠AOC=∠BOD.② 因为∠AOC=40°,所以∠BOD=40°.
在上面①到②的推导过程中,理由依据是:同角的余角相等.
故答案为:50,90,90,40;90,90,∠BOD,40,同角的余角相等.
19. 解:因为∠AOC = 120°,OE 平分∠AOC,所以∠EOC =∠AOE=60°.又因为 OD 平分∠BOC,∠BOC =30°,所以 所以∠DOE = ∠EOC-∠COD=60°-15°=45°.
20. 解:(1)设AC=2x cm,则CD,DE,EB的长度分别为3x cm,4x cm,5x cm,由题意得:2x+3x+4x+5x=56,解得x=4,则AC,CD,DE,EB 的长度分别分为8cm ,12 cm,16 cm,20cm,所以AE=AC+CD+DE=36 cm.
(2)因为M是DE的中点,所以 因为N是EB的中点,所以 所以 MN = ME +EN=18 cm.
21. 解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,其补角的度数为180°-∠AOB=180°-120°=60°.
∠DOE 与∠AOB 互补.
理由如下:因为∠DOC=35°,∠COE=∠AOE=25°,所以∠DOE=∠DOC+∠COE=60°,所以∠DOE+∠AOB=60°+120°=180°,所以∠DOE与∠AOB互补.
22. 解:(1)①若∠DCE=25°,因为∠ACD=90°,∠DCE=25°,所以∠ACE =90°-25°=65°,因为∠BCE = 90°,所以∠ACB = ∠ACE + ∠BCE =65°+90°= 155°;若∠ACB =130°,因为∠BCE=90°,所以∠ACE =130°-90°=40°,因为∠ACD=90°,所以∠DCE=90°-40°=50°,故答案为:155°;50°.
②∠ACB+∠DCE=180°,
理由如下:因为∠ACB=∠ACD+∠BCD=90°+∠BCD,所以∠ACB+∠DCE=90°+∠BCD+∠DCE,=90°+∠BCE=180°.
(2)∠DAB+∠CAE=120°,理由如下:因为∠DAB =∠DAC+∠CAB=60°+∠CAB,
所以∠DAB+∠CAE=60°+∠CAB +∠CAE=60°+∠EAB=120°.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
