一次函数基础题型练习(含答案)
图片预览



文档简介
一次函数基础题型练习
【要点梳理】
要点一、函数的相关概念
一般地,在一个变化过程中. 如果有两个变量 与,并且对于的每一个确定的值,都有唯一确定的值与其对应,那么我们就说 是自变量,是的函数.
是的函数,如果当=时=,那么叫做当自变量为时的函数值.
函数的表示方法有三种:解析式法,列表法,图象法.
要点二、一次函数的相关概念
一次函数的一般形式为,其中、是常数,≠0.特别地,当=0时,一次函数即(≠0),是正比例函数.
要点三、一次函数的图象及性质
1、函数的图象
如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
要点诠释:
直线可以看作由直线平移||个单位长度而得到(当>0时,向上平移;当<0时,向下平移).说明通过平移,函数与函数的图象之间可以相互转化.
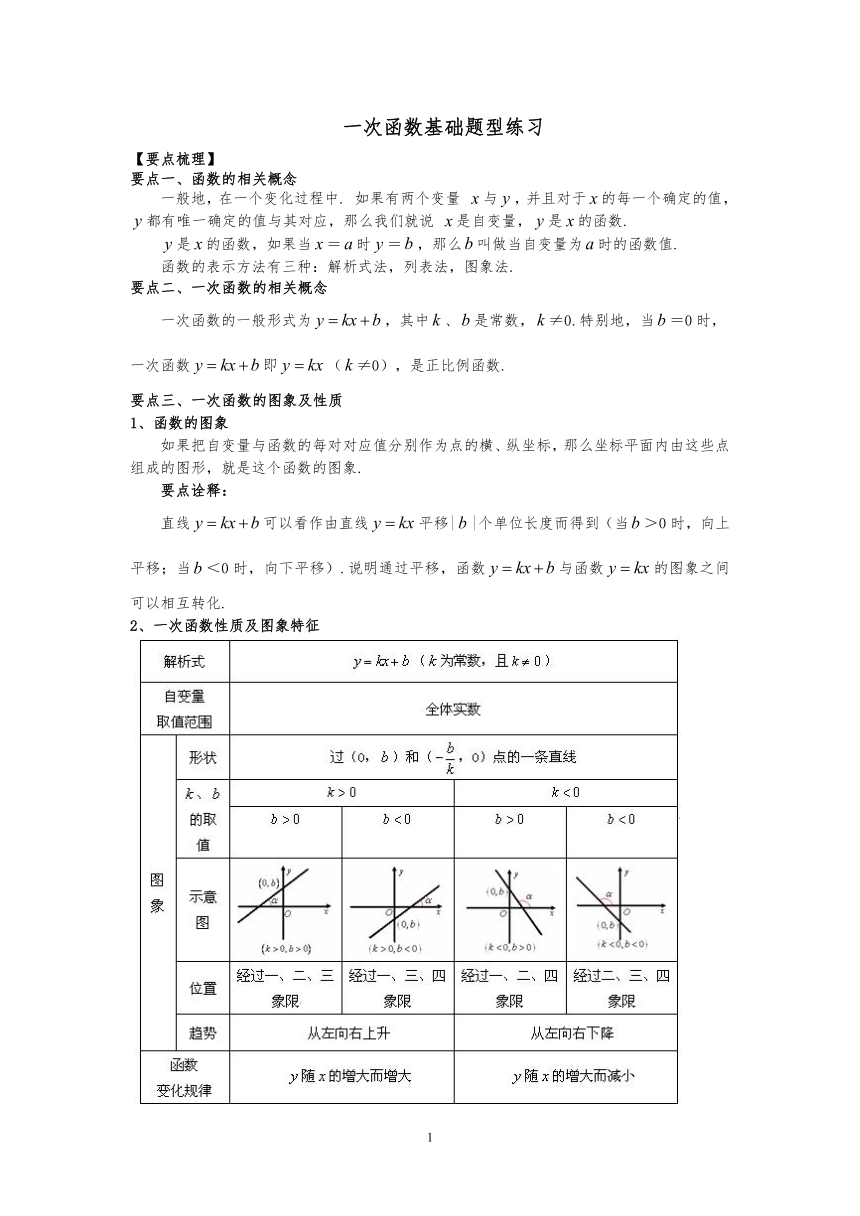
2、一次函数性质及图象特征
要点诠释:
理解、对一次函数的图象和性质的影响:
(1)决定直线从左向右的趋势(及倾斜角的大小——倾斜程度),决定它与轴交点的位置,、一起决定直线经过的象限.
(2)两条直线:和:的位置关系可由其系数确定:
与相交;
,且与平行;,且与重合;
(3)直线与一次函数图象的联系与区别
一次函数的图象是一条直线;特殊的直线、直线不是一次函数的图象.
要点四、用函数的观点看方程、方程组、不等式
方程(组)、不等式问题 函 数 问 题
从“数”的角度看 从“形”的角度看
求关于、的一元一次方程=0(≠0)的解 为何值时,函数的值为0? 确定直线与轴(即直线=0)交点的横坐标
求关于、的二元一次方程组的解. 为何值时,函数与函数的值相等? 确定直线与直线的交点的坐标
求关于的一元一次不等式>0(≠0)的解集 为何值时,函数的值大于0? 确定直线在轴(即直线=0)上方部分的所有点的横坐标的范围
一、函数定义
1、判断下列变化过程存在函数关系的是( )
A.是变量, B.人的身高与年龄 C.三角形的底边长与面积
D.速度一定的汽车所行驶的路程与时间
2、下列各曲线中不能表示y是x的函数是( )。
3、星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
A. B. C. D.
4、如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度
5.如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
A. B. C. D.
6.一水池的容积是90m3,现蓄水10m3,用水管以5m3/h的速度向水池注水,直到注满为止写出蓄水量V(m3)与注水时间t(h)之间的关系式(指出自变量t的取值范围) .
二、自变量的取值范围
1.函数y=中,自变量x的取值范围是( )
A.x且x≠1 B.x且x≠1 C.x且x≠1 D.x且x≠1
2.在函数y=中,自变量x的取值范围是( )
A.x>5 B.x≥5 C.x≠5 D.x<5
3、在函数中,自变量的取值范围是 .
4、下列函数中,自变量x的取值范围是x≥2的是( )
A.y= B.y= C.y= D.y=·
5、函数y =+中自变量x的取值范围是
A.x≤2 B.x=3 C.x<2且x ≠3 D.x ≤2且x≠3
一次函数一般式
一次函数y= kx+b与y轴交于点______,与x轴交于点 当k<0时,y随x增大而_______.当k>0时,y随x增大而
【例1】填空:已知函数y=(m-l)x+1-2m
(1)当m 时,此函数为正比例函数,当m 时,函数图像经过原点;
(2)当m 时,此函数为一次函数;
(3)当m 时,y随x增大而减小;
(4)当m 时,一次函数图像不经过第三象限;
(5)当m 时,函数图像与y=x+2的交点在x轴上;
(6)当m 时,函数图像过(0,-4)点;
(7)当m 时,函数图像平行于直线y= 2x+l;
(8)当m _时,一次函数图像交y轴于负半轴;
(9)当m 时,函数图像交x轴于正半轴.
1.下列函数中,是一次函数的有( )
(1)y=πx (2)y=2x﹣1 (3)y= (4)y=2﹣3x (5)y=x2﹣1.
A.4个 B.3个 C.2个 D.1个
2、在函数y=,y=,y=,y=x+8中,一次函数有( )
A、1个 B、2个 C、3个 D、4个
3、函数y=(m+1)+2是一次函数, m的值为( )
A、m=±1 B、m=-1 C、m=1 D、m≠-1
4、下列函数关系中,是一次函数的个数是( )
①y= ②y= ③y=210-x ④y=x2-2 ⑤ y=+1
A、1 B、2 C、3 D、4
5、一次函数y=kx+b,若k+b=1,则它的图象必经过点 ( )
A、(-1,-1)B、(-1,1)C、(1,-1)D、(1,1)
已知函数y=(m2-4)x4+n+(m-2),当m 且 时,它是一次函数;
已知y+4与x成正比例,且当x=2时,y=1,则当x=-3时,y= .
正比例函数y= kx,经过点A(2,6)、B(—1,m),则m的值
9、已知y=+,与x+2成正比,是x+1的2倍,并且当x=0时,y=4,试求函数y与x的关系式.
四、一次函数增减性
1.一次函数y=﹣x+2的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知一次函数y=kx+b﹣x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )
A.k>1,b<0 B.k>1,b>0 C.k>0,b>0 D.k>0,b<0
3.已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )
A.k<2,m>0 B.k<2,m<0 C.k>2,m>0 D.k<0,m<0
4.对于函数y=2x﹣1,下列说法正确的是( )
A.它的图象过点(1,0) B.y值随着x值增大而减小
C.它的图象经过第二象限 D.当x>1时,y>0
5.一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知P1(x1,y1),P2(x2,y2)是一次函数y=﹣x+2图象上的两点,下列判断中,正确的是( )A.y1>y2 B.y1<y2C.当x1<x2时,y1<y2 D.当x1<x2时,y1>y2
7.已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1,y2,0的大小关系是( )A.0<y1<y2 B.y1<0<y2 C.y1<y2<0 D.y2<0<y1
8、下列各组函数中,与y轴的交点相同的是( )
A、y=5x与y=2x+3 B、y=-2x+4与y=-2x-4 C、y=+3与y=-2x+3 D、y=4x-1与y=x+1
9、已知函数y=(+2)x,y随x增大而( )
A、增大 B、减小 C、与m有关 D、无法确定
10、若一次函数y=(1-2m)x+3的图象经过A(,)和B(,),当<时,<,则m的取值范围是( )
A、m<0 B、m>0 C、m< D、m>
11、已知直线y=中,若ab>0,ac<0,那么这条直线不经过( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
12.如图,正比例函数y=kx,y=mx,y=nx在同一平面直角坐标系中的图象如图所示.则比例系数k,m,n的大小关系是 .
13.一次函数与的图象如图6,则下列结论①;②;③当时,中,正确的个数是( )
A.0 B.1 C.2 D.3
14.如图,表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且 mn≠0)图像的是( ).
15、一次函数y=ax+b,ab<0,则其大致图象正确的是( )
16.已知函数的图象如图,则的图象可能是【 】
17、设b>a,将一次函数y=bx+a与y=ax+b的图象画在同一平面直角坐标系内,则有一组a,b的取值,使得下列4个图中的一个为正确的是( )
18、无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
19 .当x=5时一次函数y=2x+k和y=3kx-4的值相同,那么k和y的值分别为( )
A.1,11 B.-1,9 C.5,11 D.3,3
20、关于x的一次函数ykxk21的图象可能正确的是( )
21、如图:三个正比例函数的图像分别对应的解析式是①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是( )
A、a>b>c B、c>b>a C、b>a>c D、b>c>a
22.如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是( )
A.x>﹣5 B.x>﹣2 C.x>﹣3 D.x<﹣2
23、若实数 k,m,n 满足 k+m+n=0,且 k<n<m,则函数 y=kx+m 的图象可能是( )
A.B. C.D.
五、两直线平行
1、已知直线y=2x与直线y=kx+3互相平行,则k的值为 ( )
A、k=-2 B、k=2 C、k=±2 D、无法确定k的值
2、过点P(8,2)且与直线y=x+1平行的一次函数解析式为
3.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( ) A.y=-x-2 B.y=-x-6 C.y=-x+10 D.y=-x-1
4、一次函数的图像与y=2x-5平行且与x轴交于点(-2,0)则解析式为
5. 过点(2,-3)且平行于直线y=2x的直线是____ _____。
6. 过点(2,-3)且平行于直线y=-3x+1的直线是___________.
六、一次函数表达式的确定
1.若5y+2与x-3成正比例,则y是x的( )
A.正比例函数 B.一次函数
C.没有函数关系 D.以上答案均不正确
2.已知一次函数y=kx+b,当﹣3≤x≤1时,对应y的值为1≤y≤9,则k+b的值为 .
3.若一个正比例函数的图象经过A(3,﹣6),B(m,﹣4)两点,则m的值为( )
A.2 B.8 C.﹣2 D.﹣8
在平面直角坐标系中,如果点(x,4)在连接点(0,8)和点(-4,0)的线段上,那么x=
5.已知直线y=kx+b与直线y= -3x+7关于y轴对称,求k、b的值。
6、判断三点A(1,3)、B(-2,0)、C(2,4)是否在同一直线上 为什么
七、一次函数平移问题
1、要得到y=-x-4的图像,可把直线y=-x( ).
(A)向左平移4个单位 (B)向右平移4个单位
(C)向上平移4个单位 (D)向下平移4个单位
2.在同一平面直角坐标系中,对于函数①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是( )
A.通过点(-1,0)的是①③ B.交点在y轴上的是②④
C.相互平行的是①③ D.关于x轴对称的是②④
3. 直线向下平移2个单位,再向左平移1个单位得到直线________。
4. 直线y=向左平移2个单位得到直线
5. 直线y=2x+1向上平移4个单位得到直线
6. 直线y=-3x+5向下平移6个单位得到直线
7. 直线向上平移1个单位,再向右平移1个单位得到直线 。
8.将一次函数y=2x﹣3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( )
A.y=2x﹣5 B.y=2x+5 C.y=2x+8 D.y=2x﹣8
9.将一次函数y=2x的图象向上平移2个单位后,当y>0时,x的取值范围是( )
A.x>﹣1 B.x>1 C.x>﹣2 D.x>2
10.如图4,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),
且2m+n=6,则直线AB的解析式是( ).
A、y=-2x-3 B、y=-2x-6 C、y=-2x+3 D、y=-2x+6
11.在直角坐标系内,一次函数的图像经过三点A(2,0),B(0,2),C(,3).求这个一次函数的解析式,并求的值.
参考答案
函数定义
1、D;2、C;3、B;4、C;5、A;6、V=10+5t(0≤t≤16)
二、自变量的取值范围
1、B;2、A;3、x≥;4、D;5、D;
三、一次函数一般式
1、B;2、B;3、C;4、B;5、D;6、≠±2,n=-3;7、;8、m=-3;9、y=3x+4;
四、一次函数增减性
1、C;2、A;3、A;4、D;5、A;6、D;7、B;8、C;9、A;10、C;11、B;
12、n<m<k;13、B;14、A;15、A;16、C;17、B;18、C;19、A;20、C;21、C;
22、D;
五、两直线平行
1、B;2、y=x-6;3、C;4、y=2x+4;5、y=2x-7;6、y=-3x+3;
六、一次函数表达式的确定
1、B;2、9或-1;3、A;4、-2;5、k=-3,b=-7;6略
七、一次函数的平移
1、D;2、C;3、;4、;5、;6、;7、;
8、B;9、A;10、D;11、y=-x+2,m=-1;
【要点梳理】
要点一、函数的相关概念
一般地,在一个变化过程中. 如果有两个变量 与,并且对于的每一个确定的值,都有唯一确定的值与其对应,那么我们就说 是自变量,是的函数.
是的函数,如果当=时=,那么叫做当自变量为时的函数值.
函数的表示方法有三种:解析式法,列表法,图象法.
要点二、一次函数的相关概念
一次函数的一般形式为,其中、是常数,≠0.特别地,当=0时,一次函数即(≠0),是正比例函数.
要点三、一次函数的图象及性质
1、函数的图象
如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
要点诠释:
直线可以看作由直线平移||个单位长度而得到(当>0时,向上平移;当<0时,向下平移).说明通过平移,函数与函数的图象之间可以相互转化.
2、一次函数性质及图象特征
要点诠释:
理解、对一次函数的图象和性质的影响:
(1)决定直线从左向右的趋势(及倾斜角的大小——倾斜程度),决定它与轴交点的位置,、一起决定直线经过的象限.
(2)两条直线:和:的位置关系可由其系数确定:
与相交;
,且与平行;,且与重合;
(3)直线与一次函数图象的联系与区别
一次函数的图象是一条直线;特殊的直线、直线不是一次函数的图象.
要点四、用函数的观点看方程、方程组、不等式
方程(组)、不等式问题 函 数 问 题
从“数”的角度看 从“形”的角度看
求关于、的一元一次方程=0(≠0)的解 为何值时,函数的值为0? 确定直线与轴(即直线=0)交点的横坐标
求关于、的二元一次方程组的解. 为何值时,函数与函数的值相等? 确定直线与直线的交点的坐标
求关于的一元一次不等式>0(≠0)的解集 为何值时,函数的值大于0? 确定直线在轴(即直线=0)上方部分的所有点的横坐标的范围
一、函数定义
1、判断下列变化过程存在函数关系的是( )
A.是变量, B.人的身高与年龄 C.三角形的底边长与面积
D.速度一定的汽车所行驶的路程与时间
2、下列各曲线中不能表示y是x的函数是( )。
3、星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
A. B. C. D.
4、如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度
5.如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
A. B. C. D.
6.一水池的容积是90m3,现蓄水10m3,用水管以5m3/h的速度向水池注水,直到注满为止写出蓄水量V(m3)与注水时间t(h)之间的关系式(指出自变量t的取值范围) .
二、自变量的取值范围
1.函数y=中,自变量x的取值范围是( )
A.x且x≠1 B.x且x≠1 C.x且x≠1 D.x且x≠1
2.在函数y=中,自变量x的取值范围是( )
A.x>5 B.x≥5 C.x≠5 D.x<5
3、在函数中,自变量的取值范围是 .
4、下列函数中,自变量x的取值范围是x≥2的是( )
A.y= B.y= C.y= D.y=·
5、函数y =+中自变量x的取值范围是
A.x≤2 B.x=3 C.x<2且x ≠3 D.x ≤2且x≠3
一次函数一般式
一次函数y= kx+b与y轴交于点______,与x轴交于点 当k<0时,y随x增大而_______.当k>0时,y随x增大而
【例1】填空:已知函数y=(m-l)x+1-2m
(1)当m 时,此函数为正比例函数,当m 时,函数图像经过原点;
(2)当m 时,此函数为一次函数;
(3)当m 时,y随x增大而减小;
(4)当m 时,一次函数图像不经过第三象限;
(5)当m 时,函数图像与y=x+2的交点在x轴上;
(6)当m 时,函数图像过(0,-4)点;
(7)当m 时,函数图像平行于直线y= 2x+l;
(8)当m _时,一次函数图像交y轴于负半轴;
(9)当m 时,函数图像交x轴于正半轴.
1.下列函数中,是一次函数的有( )
(1)y=πx (2)y=2x﹣1 (3)y= (4)y=2﹣3x (5)y=x2﹣1.
A.4个 B.3个 C.2个 D.1个
2、在函数y=,y=,y=,y=x+8中,一次函数有( )
A、1个 B、2个 C、3个 D、4个
3、函数y=(m+1)+2是一次函数, m的值为( )
A、m=±1 B、m=-1 C、m=1 D、m≠-1
4、下列函数关系中,是一次函数的个数是( )
①y= ②y= ③y=210-x ④y=x2-2 ⑤ y=+1
A、1 B、2 C、3 D、4
5、一次函数y=kx+b,若k+b=1,则它的图象必经过点 ( )
A、(-1,-1)B、(-1,1)C、(1,-1)D、(1,1)
已知函数y=(m2-4)x4+n+(m-2),当m 且 时,它是一次函数;
已知y+4与x成正比例,且当x=2时,y=1,则当x=-3时,y= .
正比例函数y= kx,经过点A(2,6)、B(—1,m),则m的值
9、已知y=+,与x+2成正比,是x+1的2倍,并且当x=0时,y=4,试求函数y与x的关系式.
四、一次函数增减性
1.一次函数y=﹣x+2的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知一次函数y=kx+b﹣x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )
A.k>1,b<0 B.k>1,b>0 C.k>0,b>0 D.k>0,b<0
3.已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )
A.k<2,m>0 B.k<2,m<0 C.k>2,m>0 D.k<0,m<0
4.对于函数y=2x﹣1,下列说法正确的是( )
A.它的图象过点(1,0) B.y值随着x值增大而减小
C.它的图象经过第二象限 D.当x>1时,y>0
5.一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知P1(x1,y1),P2(x2,y2)是一次函数y=﹣x+2图象上的两点,下列判断中,正确的是( )A.y1>y2 B.y1<y2C.当x1<x2时,y1<y2 D.当x1<x2时,y1>y2
7.已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1,y2,0的大小关系是( )A.0<y1<y2 B.y1<0<y2 C.y1<y2<0 D.y2<0<y1
8、下列各组函数中,与y轴的交点相同的是( )
A、y=5x与y=2x+3 B、y=-2x+4与y=-2x-4 C、y=+3与y=-2x+3 D、y=4x-1与y=x+1
9、已知函数y=(+2)x,y随x增大而( )
A、增大 B、减小 C、与m有关 D、无法确定
10、若一次函数y=(1-2m)x+3的图象经过A(,)和B(,),当<时,<,则m的取值范围是( )
A、m<0 B、m>0 C、m< D、m>
11、已知直线y=中,若ab>0,ac<0,那么这条直线不经过( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
12.如图,正比例函数y=kx,y=mx,y=nx在同一平面直角坐标系中的图象如图所示.则比例系数k,m,n的大小关系是 .
13.一次函数与的图象如图6,则下列结论①;②;③当时,中,正确的个数是( )
A.0 B.1 C.2 D.3
14.如图,表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且 mn≠0)图像的是( ).
15、一次函数y=ax+b,ab<0,则其大致图象正确的是( )
16.已知函数的图象如图,则的图象可能是【 】
17、设b>a,将一次函数y=bx+a与y=ax+b的图象画在同一平面直角坐标系内,则有一组a,b的取值,使得下列4个图中的一个为正确的是( )
18、无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
19 .当x=5时一次函数y=2x+k和y=3kx-4的值相同,那么k和y的值分别为( )
A.1,11 B.-1,9 C.5,11 D.3,3
20、关于x的一次函数ykxk21的图象可能正确的是( )
21、如图:三个正比例函数的图像分别对应的解析式是①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是( )
A、a>b>c B、c>b>a C、b>a>c D、b>c>a
22.如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是( )
A.x>﹣5 B.x>﹣2 C.x>﹣3 D.x<﹣2
23、若实数 k,m,n 满足 k+m+n=0,且 k<n<m,则函数 y=kx+m 的图象可能是( )
A.B. C.D.
五、两直线平行
1、已知直线y=2x与直线y=kx+3互相平行,则k的值为 ( )
A、k=-2 B、k=2 C、k=±2 D、无法确定k的值
2、过点P(8,2)且与直线y=x+1平行的一次函数解析式为
3.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( ) A.y=-x-2 B.y=-x-6 C.y=-x+10 D.y=-x-1
4、一次函数的图像与y=2x-5平行且与x轴交于点(-2,0)则解析式为
5. 过点(2,-3)且平行于直线y=2x的直线是____ _____。
6. 过点(2,-3)且平行于直线y=-3x+1的直线是___________.
六、一次函数表达式的确定
1.若5y+2与x-3成正比例,则y是x的( )
A.正比例函数 B.一次函数
C.没有函数关系 D.以上答案均不正确
2.已知一次函数y=kx+b,当﹣3≤x≤1时,对应y的值为1≤y≤9,则k+b的值为 .
3.若一个正比例函数的图象经过A(3,﹣6),B(m,﹣4)两点,则m的值为( )
A.2 B.8 C.﹣2 D.﹣8
在平面直角坐标系中,如果点(x,4)在连接点(0,8)和点(-4,0)的线段上,那么x=
5.已知直线y=kx+b与直线y= -3x+7关于y轴对称,求k、b的值。
6、判断三点A(1,3)、B(-2,0)、C(2,4)是否在同一直线上 为什么
七、一次函数平移问题
1、要得到y=-x-4的图像,可把直线y=-x( ).
(A)向左平移4个单位 (B)向右平移4个单位
(C)向上平移4个单位 (D)向下平移4个单位
2.在同一平面直角坐标系中,对于函数①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是( )
A.通过点(-1,0)的是①③ B.交点在y轴上的是②④
C.相互平行的是①③ D.关于x轴对称的是②④
3. 直线向下平移2个单位,再向左平移1个单位得到直线________。
4. 直线y=向左平移2个单位得到直线
5. 直线y=2x+1向上平移4个单位得到直线
6. 直线y=-3x+5向下平移6个单位得到直线
7. 直线向上平移1个单位,再向右平移1个单位得到直线 。
8.将一次函数y=2x﹣3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( )
A.y=2x﹣5 B.y=2x+5 C.y=2x+8 D.y=2x﹣8
9.将一次函数y=2x的图象向上平移2个单位后,当y>0时,x的取值范围是( )
A.x>﹣1 B.x>1 C.x>﹣2 D.x>2
10.如图4,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),
且2m+n=6,则直线AB的解析式是( ).
A、y=-2x-3 B、y=-2x-6 C、y=-2x+3 D、y=-2x+6
11.在直角坐标系内,一次函数的图像经过三点A(2,0),B(0,2),C(,3).求这个一次函数的解析式,并求的值.
参考答案
函数定义
1、D;2、C;3、B;4、C;5、A;6、V=10+5t(0≤t≤16)
二、自变量的取值范围
1、B;2、A;3、x≥;4、D;5、D;
三、一次函数一般式
1、B;2、B;3、C;4、B;5、D;6、≠±2,n=-3;7、;8、m=-3;9、y=3x+4;
四、一次函数增减性
1、C;2、A;3、A;4、D;5、A;6、D;7、B;8、C;9、A;10、C;11、B;
12、n<m<k;13、B;14、A;15、A;16、C;17、B;18、C;19、A;20、C;21、C;
22、D;
五、两直线平行
1、B;2、y=x-6;3、C;4、y=2x+4;5、y=2x-7;6、y=-3x+3;
六、一次函数表达式的确定
1、B;2、9或-1;3、A;4、-2;5、k=-3,b=-7;6略
七、一次函数的平移
1、D;2、C;3、;4、;5、;6、;7、;
8、B;9、A;10、D;11、y=-x+2,m=-1;
