湘教八下1.1.1直角三角形的性质和判定 课件
文档属性
| 名称 | 湘教八下1.1.1直角三角形的性质和判定 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 991.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 08:32:43 | ||
图片预览



文档简介
(共25张PPT)
第一章 直角三角形
1.1.1直角三角形的性质和判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
掌握直角三角形的性质和判定;
01
能正确掌握直角三角形斜边上的中线性质定理的应用;
02
提高学生对直角三角形斜边上的中线性质定理的探索过程及证明思想方法。
03
02
新知导入
三角形顶点与对边中点的连线段。
1.直角三角形的定义
2.三角形内角和的性质
有一个是直角的三角形叫直角三角形。
三角形内角和等于180°。
3.三角形中线的定义
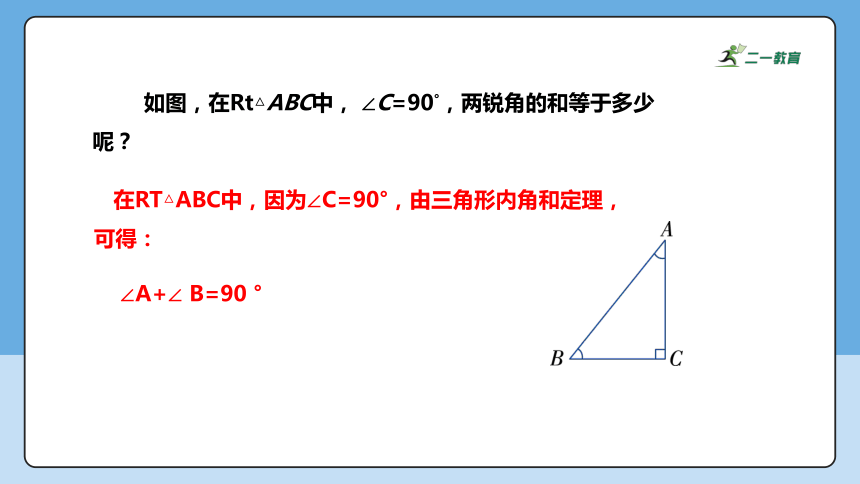
如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
∠A+∠ B=90 °
在RT△ABC中,因为∠C=90°,由三角形内角和定理,可得:
03
新知探究
结论
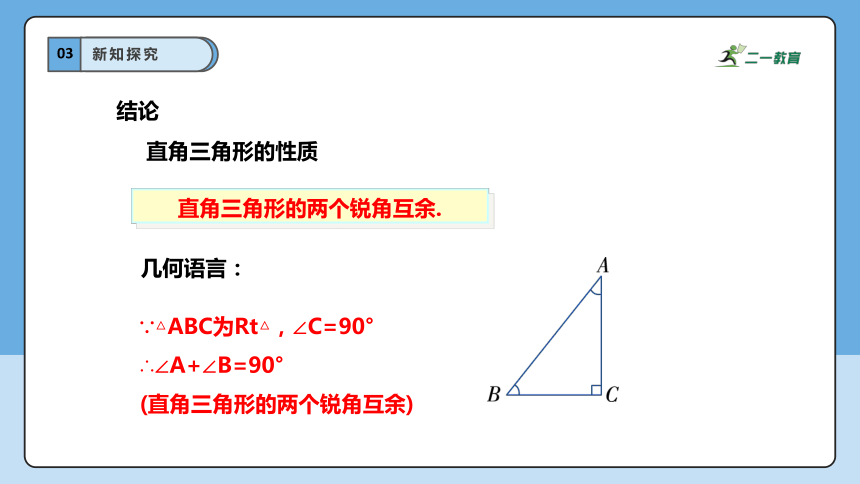
直角三角形的两个锐角互余.
直角三角形的性质
几何语言:
∵△ABC为Rt△,∠C=90°
∴∠A+∠B=90°
(直角三角形的两个锐角互余)
新课探究
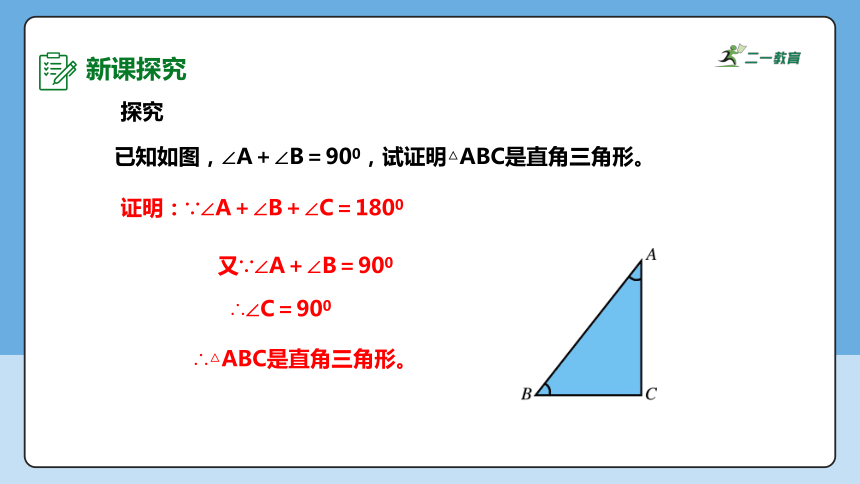
探究
证明:∵∠A+∠B+∠C=1800
又∵∠A+∠B=900
∴∠C=900
∴△ABC是直角三角形。
已知如图,∠A+∠B=900,试证明△ABC是直角三角形。
03
新知探究
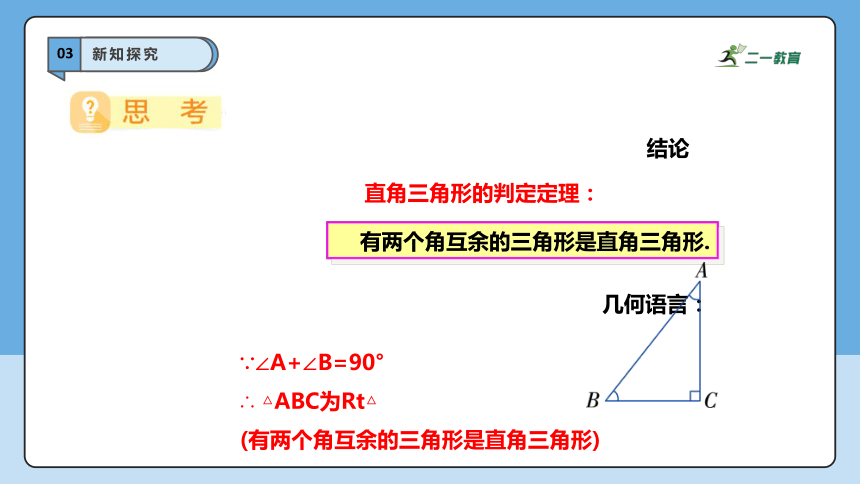
有两个角互余的三角形是直角三角形.
直角三角形的判定定理:
结论
几何语言:
∵∠A+∠B=90°
∴ △ABC为Rt△
(有两个角互余的三角形是直角三角形)
03
新知探究
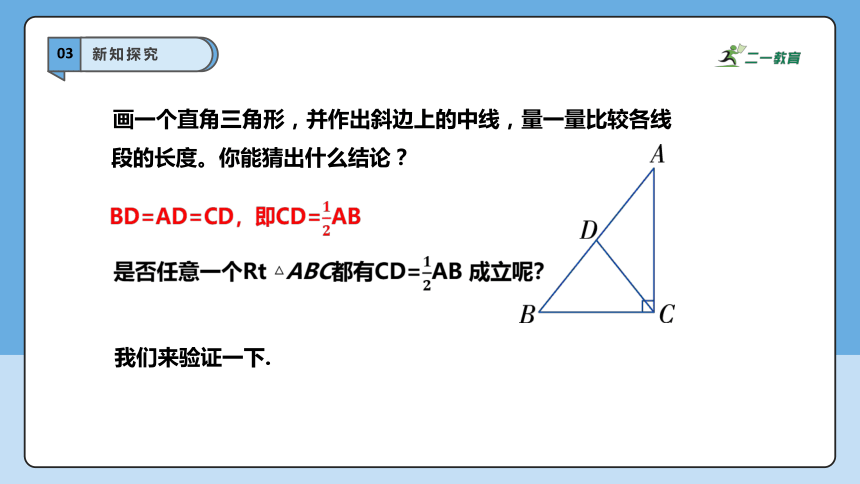
画一个直角三角形,并作出斜边上的中线,量一量比较各线段的长度。你能猜出什么结论?
我们来验证一下.
是否任意一个Rt △ABC都有CD=AB 成立呢?
BD=AD=CD,即CD=AB
图1-4
如图1-3, 如果中线CD =AB,则有∠DCA = ∠A .
由此受到启发,在图1-4 的Rt△ABC中,过直角顶点C作射线CD’交AB于D’,使 ∠D’CA=∠A,则CD’=AD’
图1-3
∠A +∠B=90° , ∠D’CA +∠D’CB=90°
又∵
故得CD’=AD’=BD’=
∴ 点D’是斜边上的中点,即CD’是斜边AB的中线.
从而CD与BD’重合,且CD=
∴ ∠B= ∠D’CB
∴CD’=BD’
结论
直角三角形斜边上的中线等于斜边的一半.
直角三角形的性质定理:
几何语言:
∵△ABC为Rt△,∠C=90°
∴CD=AB
(直角三角形斜边上的中线等于斜边的一半)
03
新知讲解
例1
已知:如图1-5,CD是△ABC的AB边上的中
线,且.
求证:△ABC是直角三角形.
03
新知讲解
证明:∵ ,
∴∠1=∠A,(等边对等角)
∠2=∠B .
根据三角形内角和性质,有
∠A+∠B+∠ACB =180°,
即得∠A+∠B+∠1+∠2=180°,
2(∠A+∠B)=180°.
∴∠A+∠B =90°.
∴ △ABC是直角三角形
04
课堂练习
【知识技能类作业】必做题:
1.在Rt△ABC中,∠C=90°,∠A -∠B =30°,那么∠A=( )
A. 90° B. 80° C. 70° D. 60°
2.如图, 在△ABC中,∠ACB=90°,D是AB的中点
则图中等腰三角形的个数有( )
A. 4个 B. 3个 C. 2个 D. 1个
D
C
04
课堂练习
【知识技能类作业】选做题:
3、已知,Rt△ABC中,∠ACB=90°,CD⊥AB,CE为AB边上的中线,且∠BCD=3∠DCA。
求证:DE=DC。
证明:∵∠BCD=3∠DCA且∠BCA=90°
∴∠DCA=22. 5°∠BCD=67.5°∠B=22.5°
∴∠CEA=45°∠ECD=67.5°-22.5°=45°
∴DE=DC
04
课堂练习
【综合拓展类作业】
4.如图,AB∥CD,∠BAC和∠ACD的平分线相交于H点,E为AC的中点,EH=2.那么△AHC是直角三角形吗?为什么?若是,求出AC的长.
04
课堂练习
【综合拓展类作业】
由EH=2 易知AC=4.
证明:∵ AB∥CD,∴ ∠BAC+∠DCA=180°.
又∠CAH=∠BAC ,∠ACH=∠DCA,
∴△AHC是直角三角形.
在Rt△AHC中,EH为斜边上的中线,
∵∠CAH+∠ACH=
∴EH=
05
课堂小结
(1)直角三角形的两个锐角互余。
(2)在直角三角形中,斜边上的中线等于斜边的一半.
直角三角形的判定:
直角三角形的有关性质:
(1)有两个角互余的三角形是直角三角形.
(2)如果三角形一边上的中线等于这条边的一半,这个三角形是直角三角形。
直角三角形的性质与判定
06
作业布置
【知识技能类作业】必做题:
1、 在△ABC中,∠ACB=90°,D是AB的中点,CD=5,CE⊥AB,CE=4,则△ABC的面积是 。
20
2、如图,AB∥CD,∠A和∠C的平分线相交于H点,△AHC
是 三角形。
直角
06
作业布置
【知识技能类作业】选做题:
3.△ABC中,∠A=∠B,∠B=∠C,∠A= ,∠B= .∠C= .
20°
40°
120°
06
作业布置
【综合拓展类作业】
4、在△ABC中,∠ACB=90°,D是AB边的中点,点F在AC边上,DE与CF平行且相等。
求证:AE=DF。
06
作业布置
【综合拓展类作业】
解:∵在Rt△ACB中,D为AB中点,
∴CD=AB=AD
∵DE∥CF ∴∠1=∠2 ∴∠1=∠3
∴在△DEA与△DFC中
∴△EDA≌△DFC(SAS)
∴AE=DF
∴∠2=∠3
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
1.1.1直角三角形的性质和判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
掌握直角三角形的性质和判定;
01
能正确掌握直角三角形斜边上的中线性质定理的应用;
02
提高学生对直角三角形斜边上的中线性质定理的探索过程及证明思想方法。
03
02
新知导入
三角形顶点与对边中点的连线段。
1.直角三角形的定义
2.三角形内角和的性质
有一个是直角的三角形叫直角三角形。
三角形内角和等于180°。
3.三角形中线的定义
如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
∠A+∠ B=90 °
在RT△ABC中,因为∠C=90°,由三角形内角和定理,可得:
03
新知探究
结论
直角三角形的两个锐角互余.
直角三角形的性质
几何语言:
∵△ABC为Rt△,∠C=90°
∴∠A+∠B=90°
(直角三角形的两个锐角互余)
新课探究
探究
证明:∵∠A+∠B+∠C=1800
又∵∠A+∠B=900
∴∠C=900
∴△ABC是直角三角形。
已知如图,∠A+∠B=900,试证明△ABC是直角三角形。
03
新知探究
有两个角互余的三角形是直角三角形.
直角三角形的判定定理:
结论
几何语言:
∵∠A+∠B=90°
∴ △ABC为Rt△
(有两个角互余的三角形是直角三角形)
03
新知探究
画一个直角三角形,并作出斜边上的中线,量一量比较各线段的长度。你能猜出什么结论?
我们来验证一下.
是否任意一个Rt △ABC都有CD=AB 成立呢?
BD=AD=CD,即CD=AB
图1-4
如图1-3, 如果中线CD =AB,则有∠DCA = ∠A .
由此受到启发,在图1-4 的Rt△ABC中,过直角顶点C作射线CD’交AB于D’,使 ∠D’CA=∠A,则CD’=AD’
图1-3
∠A +∠B=90° , ∠D’CA +∠D’CB=90°
又∵
故得CD’=AD’=BD’=
∴ 点D’是斜边上的中点,即CD’是斜边AB的中线.
从而CD与BD’重合,且CD=
∴ ∠B= ∠D’CB
∴CD’=BD’
结论
直角三角形斜边上的中线等于斜边的一半.
直角三角形的性质定理:
几何语言:
∵△ABC为Rt△,∠C=90°
∴CD=AB
(直角三角形斜边上的中线等于斜边的一半)
03
新知讲解
例1
已知:如图1-5,CD是△ABC的AB边上的中
线,且.
求证:△ABC是直角三角形.
03
新知讲解
证明:∵ ,
∴∠1=∠A,(等边对等角)
∠2=∠B .
根据三角形内角和性质,有
∠A+∠B+∠ACB =180°,
即得∠A+∠B+∠1+∠2=180°,
2(∠A+∠B)=180°.
∴∠A+∠B =90°.
∴ △ABC是直角三角形
04
课堂练习
【知识技能类作业】必做题:
1.在Rt△ABC中,∠C=90°,∠A -∠B =30°,那么∠A=( )
A. 90° B. 80° C. 70° D. 60°
2.如图, 在△ABC中,∠ACB=90°,D是AB的中点
则图中等腰三角形的个数有( )
A. 4个 B. 3个 C. 2个 D. 1个
D
C
04
课堂练习
【知识技能类作业】选做题:
3、已知,Rt△ABC中,∠ACB=90°,CD⊥AB,CE为AB边上的中线,且∠BCD=3∠DCA。
求证:DE=DC。
证明:∵∠BCD=3∠DCA且∠BCA=90°
∴∠DCA=22. 5°∠BCD=67.5°∠B=22.5°
∴∠CEA=45°∠ECD=67.5°-22.5°=45°
∴DE=DC
04
课堂练习
【综合拓展类作业】
4.如图,AB∥CD,∠BAC和∠ACD的平分线相交于H点,E为AC的中点,EH=2.那么△AHC是直角三角形吗?为什么?若是,求出AC的长.
04
课堂练习
【综合拓展类作业】
由EH=2 易知AC=4.
证明:∵ AB∥CD,∴ ∠BAC+∠DCA=180°.
又∠CAH=∠BAC ,∠ACH=∠DCA,
∴△AHC是直角三角形.
在Rt△AHC中,EH为斜边上的中线,
∵∠CAH+∠ACH=
∴EH=
05
课堂小结
(1)直角三角形的两个锐角互余。
(2)在直角三角形中,斜边上的中线等于斜边的一半.
直角三角形的判定:
直角三角形的有关性质:
(1)有两个角互余的三角形是直角三角形.
(2)如果三角形一边上的中线等于这条边的一半,这个三角形是直角三角形。
直角三角形的性质与判定
06
作业布置
【知识技能类作业】必做题:
1、 在△ABC中,∠ACB=90°,D是AB的中点,CD=5,CE⊥AB,CE=4,则△ABC的面积是 。
20
2、如图,AB∥CD,∠A和∠C的平分线相交于H点,△AHC
是 三角形。
直角
06
作业布置
【知识技能类作业】选做题:
3.△ABC中,∠A=∠B,∠B=∠C,∠A= ,∠B= .∠C= .
20°
40°
120°
06
作业布置
【综合拓展类作业】
4、在△ABC中,∠ACB=90°,D是AB边的中点,点F在AC边上,DE与CF平行且相等。
求证:AE=DF。
06
作业布置
【综合拓展类作业】
解:∵在Rt△ACB中,D为AB中点,
∴CD=AB=AD
∵DE∥CF ∴∠1=∠2 ∴∠1=∠3
∴在△DEA与△DFC中
∴△EDA≌△DFC(SAS)
∴AE=DF
∴∠2=∠3
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
