1.1 数列的概念 教案(表格式)-2024-2025学年高二上学期数学湘教版(2019)选择性必修第一册
文档属性
| 名称 | 1.1 数列的概念 教案(表格式)-2024-2025学年高二上学期数学湘教版(2019)选择性必修第一册 | 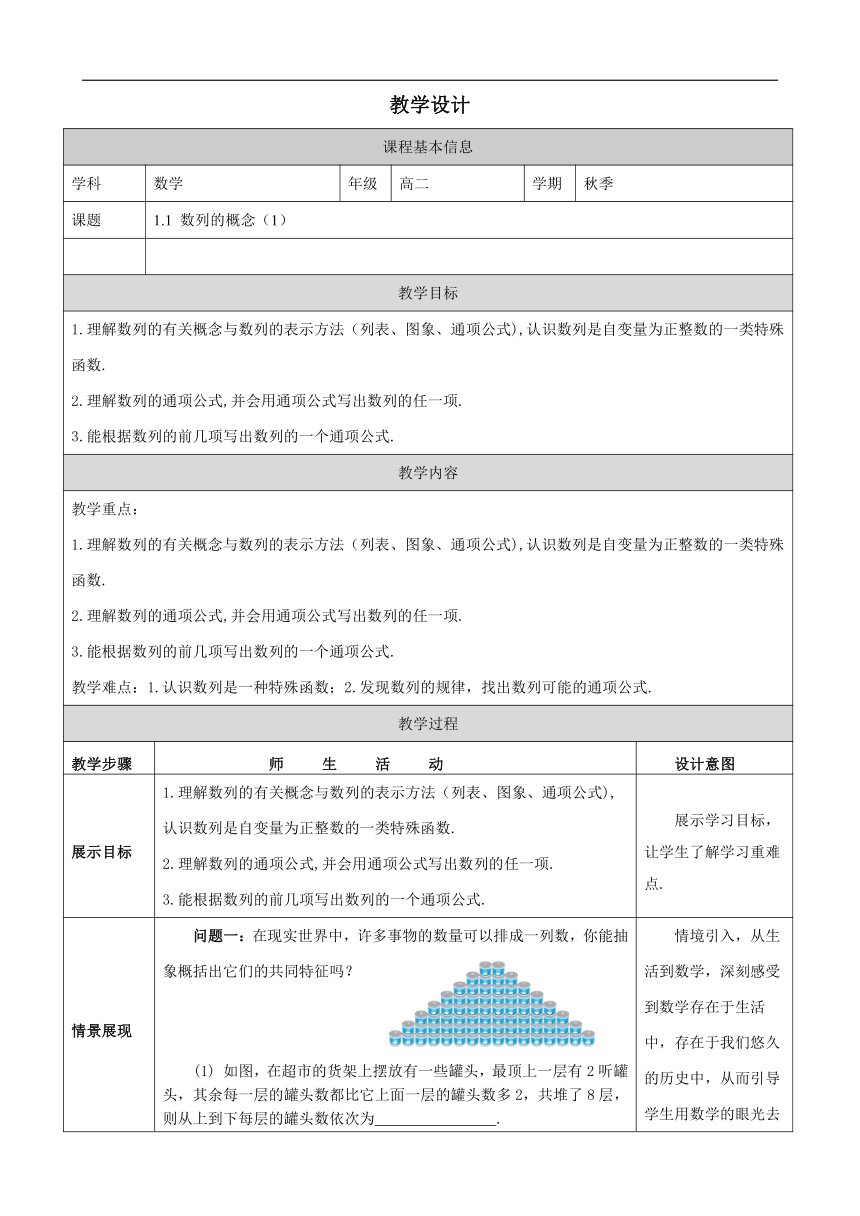 | |
| 格式 | docx | ||
| 文件大小 | 142.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 13:46:42 | ||
图片预览


文档简介
教学设计
课程基本信息
学科 数学 年级 高二 学期 秋季
课题 1.1 数列的概念(1)
教学目标
1.理解数列的有关概念与数列的表示方法(列表、图象、通项公式),认识数列是自变量为正整数的一类特殊函数. 2.理解数列的通项公式,并会用通项公式写出数列的任一项. 3.能根据数列的前几项写出数列的一个通项公式.
教学内容
教学重点: 1.理解数列的有关概念与数列的表示方法(列表、图象、通项公式),认识数列是自变量为正整数的一类特殊函数. 2.理解数列的通项公式,并会用通项公式写出数列的任一项. 3.能根据数列的前几项写出数列的一个通项公式. 教学难点:1.认识数列是一种特殊函数;2.发现数列的规律,找出数列可能的通项公式.
教学过程
教学步骤 师 生 活 动 设计意图
展示目标 1.理解数列的有关概念与数列的表示方法(列表、图象、通项公式),认识数列是自变量为正整数的一类特殊函数. 2.理解数列的通项公式,并会用通项公式写出数列的任一项. 3.能根据数列的前几项写出数列的一个通项公式. 展示学习目标,让学生了解学习重难点.
情景展现 问题一:在现实世界中,许多事物的数量可以排成一列数,你能抽象概括出它们的共同特征吗? (1) 如图,在超市的货架上摆放有一些罐头,最顶上一层有2听罐头,其余每一层的罐头数都比它上面一层的罐头数多2,共堆了8层, 则从上到下每层的罐头数依次为 . (2) 《庄子·天下》有一句话:“一尺之棰,日取其半,万世不竭”.用数学的方法如何理解? (3)某家庭一年内1—12月的用电量(单位kW·h)依次为:110,120,90,80,62,80,103,115,84,65,81,95. (4)的正弦值依次为:. (5)正整数1,2,3,4,5,6,┉被3除的余数依次为: 1,2,0,1,2,0,1,2,0,┉. 情境引入,从生活到数学,深刻感受到数学存在于生活中,存在于我们悠久的历史中,从而引导学生用数学的眼光去观察世界. 通过对问题一的探究,抓住了学生的注意力,把学生的思维引到数列的概念来,此时再把问题概念化,进入第二环节.
自主探究 一、数列的定义: 按照一定顺序排成的一列数叫做数列,数列中的每一个数叫做这个数列的项,排在第一位的数叫作数列的首项或叫作数列的第1项,排在第二位的数叫作数列的第2项,…,排在第n位的数叫作数列的第n项. 数列的一般形式:简记为. 二、数列的分类 项数有限的数列称为有穷数列,项数无限的数列称为无穷数列. 数列的通项公式:如果数列的第n项与序号n之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.记作. 让学生的学习由感性到理性,生成严谨的数列定义,理解数列从项数的角度可以分为有穷数列和无穷数列.
发现问题 思考1.可以看作的一个函数,那么它的定义域是什么? 思考2.利用一个数列的通项公式,你能确定这个数列哪些方面的性质? 思考3.函数的表示法有解析式法、列表法、图象法,数列有吗?数列的图象有什么特点? 引导学生看书第3页到第4页 这一环节首先让学生自主思考,然后小组交流,得出从函数的观点看:数列的通项公式就是数列的解析表达式.
问题解决 应用一:已知数列的通项公式求其指定项 例1.根据数列的通项公式,写出数列的前5项及第n+1项. (1); (2). 应用二:已知数列的前若干项求其通项公式 例2.观察下面各数列,试着找出它的一个通项公式: (1)2,4,2,4,…; (2)9,99,999,9999,…; (3),,,,…. 让学生理性认识与感性认识相结合,直观想象与逻辑推理相结合,两道例题问题恰好相反,帮助学生掌握如何求已知数列中的指定项,以及由数列的前若干项如何写出一个合适的通项公式.
课堂练习 练习 写出下列数列的一个通项公式,使它的前4项分别是下列各数: 课本第5页3,4题 落实课堂教学目标,巩固例题教学成果,使学生进一步理解和灵活应用数列的通项公式.
课堂小结 我们学到了哪些新的数学知识? 1.知识清单: (1)理解数列的有关概念与数列的表示方法(列表、图象、通项公式),认识数列是自变量为正整数的一类特殊函数. (2)有穷数列、无穷数列. (3)理解数列的通项公式,并会用通项公式写出数列的任一项,能根据数列的前几项写出数列的一个通项公式. 二、我们运用了哪些解题方法和数学思想? 1.方法归纳:观察、归纳、猜想. 2.常见误区:归纳法求数列的通项公式时归纳不全面;不注意用(-1)n进行调节,不注意分子、分母间的联系. 系统梳理整节课所学内容.
课后作业 书本作业:习题1.1 1,4,5 补充作业; 在数列{an}中,an=-2n2+9n+3. (1)求; (2)-107是不是该数列中的某一项 若是,是第几项 (3)求数列中的最大项. 巩固深化.
板书设计 一、数列的定义 1.数列;2.数列的项 二、数列的分类 1.有穷数列;2.无穷数列. 三、数列的表示方法 1. 解析式法(通项公式) 2. 列表法 3. 图象法 四、通项公式的应用 例1. 例2. 展示课堂教学重点和例题示范,解题思路.
课后反思
课程基本信息
学科 数学 年级 高二 学期 秋季
课题 1.1 数列的概念(1)
教学目标
1.理解数列的有关概念与数列的表示方法(列表、图象、通项公式),认识数列是自变量为正整数的一类特殊函数. 2.理解数列的通项公式,并会用通项公式写出数列的任一项. 3.能根据数列的前几项写出数列的一个通项公式.
教学内容
教学重点: 1.理解数列的有关概念与数列的表示方法(列表、图象、通项公式),认识数列是自变量为正整数的一类特殊函数. 2.理解数列的通项公式,并会用通项公式写出数列的任一项. 3.能根据数列的前几项写出数列的一个通项公式. 教学难点:1.认识数列是一种特殊函数;2.发现数列的规律,找出数列可能的通项公式.
教学过程
教学步骤 师 生 活 动 设计意图
展示目标 1.理解数列的有关概念与数列的表示方法(列表、图象、通项公式),认识数列是自变量为正整数的一类特殊函数. 2.理解数列的通项公式,并会用通项公式写出数列的任一项. 3.能根据数列的前几项写出数列的一个通项公式. 展示学习目标,让学生了解学习重难点.
情景展现 问题一:在现实世界中,许多事物的数量可以排成一列数,你能抽象概括出它们的共同特征吗? (1) 如图,在超市的货架上摆放有一些罐头,最顶上一层有2听罐头,其余每一层的罐头数都比它上面一层的罐头数多2,共堆了8层, 则从上到下每层的罐头数依次为 . (2) 《庄子·天下》有一句话:“一尺之棰,日取其半,万世不竭”.用数学的方法如何理解? (3)某家庭一年内1—12月的用电量(单位kW·h)依次为:110,120,90,80,62,80,103,115,84,65,81,95. (4)的正弦值依次为:. (5)正整数1,2,3,4,5,6,┉被3除的余数依次为: 1,2,0,1,2,0,1,2,0,┉. 情境引入,从生活到数学,深刻感受到数学存在于生活中,存在于我们悠久的历史中,从而引导学生用数学的眼光去观察世界. 通过对问题一的探究,抓住了学生的注意力,把学生的思维引到数列的概念来,此时再把问题概念化,进入第二环节.
自主探究 一、数列的定义: 按照一定顺序排成的一列数叫做数列,数列中的每一个数叫做这个数列的项,排在第一位的数叫作数列的首项或叫作数列的第1项,排在第二位的数叫作数列的第2项,…,排在第n位的数叫作数列的第n项. 数列的一般形式:简记为. 二、数列的分类 项数有限的数列称为有穷数列,项数无限的数列称为无穷数列. 数列的通项公式:如果数列的第n项与序号n之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.记作. 让学生的学习由感性到理性,生成严谨的数列定义,理解数列从项数的角度可以分为有穷数列和无穷数列.
发现问题 思考1.可以看作的一个函数,那么它的定义域是什么? 思考2.利用一个数列的通项公式,你能确定这个数列哪些方面的性质? 思考3.函数的表示法有解析式法、列表法、图象法,数列有吗?数列的图象有什么特点? 引导学生看书第3页到第4页 这一环节首先让学生自主思考,然后小组交流,得出从函数的观点看:数列的通项公式就是数列的解析表达式.
问题解决 应用一:已知数列的通项公式求其指定项 例1.根据数列的通项公式,写出数列的前5项及第n+1项. (1); (2). 应用二:已知数列的前若干项求其通项公式 例2.观察下面各数列,试着找出它的一个通项公式: (1)2,4,2,4,…; (2)9,99,999,9999,…; (3),,,,…. 让学生理性认识与感性认识相结合,直观想象与逻辑推理相结合,两道例题问题恰好相反,帮助学生掌握如何求已知数列中的指定项,以及由数列的前若干项如何写出一个合适的通项公式.
课堂练习 练习 写出下列数列的一个通项公式,使它的前4项分别是下列各数: 课本第5页3,4题 落实课堂教学目标,巩固例题教学成果,使学生进一步理解和灵活应用数列的通项公式.
课堂小结 我们学到了哪些新的数学知识? 1.知识清单: (1)理解数列的有关概念与数列的表示方法(列表、图象、通项公式),认识数列是自变量为正整数的一类特殊函数. (2)有穷数列、无穷数列. (3)理解数列的通项公式,并会用通项公式写出数列的任一项,能根据数列的前几项写出数列的一个通项公式. 二、我们运用了哪些解题方法和数学思想? 1.方法归纳:观察、归纳、猜想. 2.常见误区:归纳法求数列的通项公式时归纳不全面;不注意用(-1)n进行调节,不注意分子、分母间的联系. 系统梳理整节课所学内容.
课后作业 书本作业:习题1.1 1,4,5 补充作业; 在数列{an}中,an=-2n2+9n+3. (1)求; (2)-107是不是该数列中的某一项 若是,是第几项 (3)求数列中的最大项. 巩固深化.
板书设计 一、数列的定义 1.数列;2.数列的项 二、数列的分类 1.有穷数列;2.无穷数列. 三、数列的表示方法 1. 解析式法(通项公式) 2. 列表法 3. 图象法 四、通项公式的应用 例1. 例2. 展示课堂教学重点和例题示范,解题思路.
课后反思
同课章节目录
