2024-2025学年四川省绵阳市三台县高二(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年四川省绵阳市三台县高二(上)期中数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 174.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 13:59:10 | ||
图片预览



文档简介
2024-2025学年四川省绵阳市三台县高二(上)期中
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.对总数为的一批零件抽取一个容量为的样本,若每个零件被抽取的概率为,则等于( )
A. B. C. D.
2.已知点是点在坐标平面内的射影,则( )
A. B. C. D.
3.如图,空间四边形中,,,,点在上,且,点为中点,则等于( )
A.
B.
C.
D.
4.甲,乙两人独立地破解同一个谜题,破解出谜题的概率分别为,,则谜题被破解的概率为( )
A. B. C. D.
5.是空气质量的一个重要指标,我国标准采用世卫组织设定的最宽限值,即日均值在以下空气质量为一级,在之间空气质量为二级,在以上空气质量为超标如图是某地月日到日日均值单位:的统计数据,则下列叙述错误的是( )
A. 从这天的日均监测数据中随机抽出一天的数据,空气质量为一级的概率是
B. 从日到日,日均值逐渐降低
C. 这天中日均值的平均数是
D. 这天的日均值的中位数是
6.下列说法正确的是( )
A. 如果一组数据的中位数比平均数小很多,则这组数据是近似对称的
B. 若,,三点不共线,平面外一点,若,则,,,四点共面
C. 已知空间直角坐标系中的三点、、,则点到直线的距离为
D. 有人从一座层大楼的底层进入电梯,假设每个人自第二层开始在每一层离开电梯是等可能的,则该人在不同层离开电梯的概率是
7.如图,平行六面体的所有棱长为,四边形是正方形,,点是与的交点,则直线与所成角的余弦值为( )
A. B. C. D.
8.柜子里有双不同的鞋,从中随机地取出只,记事件“取出的鞋不成双”,事件“取出的鞋都是一只脚的”,事件“取出的鞋子是一只左脚一只右脚的,但不是一双鞋”则有( )
A. B. 与相互独立
C. D. 与互斥
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.北京时间年月日,我国射击健将黄雨婷、盛李豪在奥运会上战胜韩国选手,摘夺了射击混合团体米气步枪金牌,通过赛后数据记录得到其中一名选手的得分分别为,,,,,,,则( )
A. 该组数据的极差为
B. 该组数据的众数为
C. 该组数据的分位数为
D. 若该组数据去掉一个最高分和最低分,则这组数据的方差变小
10.如图,在四面体中,,,,分别是,,,的中点则以下四个结论正确的是( )
A. 向量,,共面
B. 平面
C. 若四面体各棱长均为,则
D. 若是和的交点,则对空间任意一点,有
11.人类的四种血型与基因类型的对应为:型的基因类型为,型的基因类型为或,型的基因类型为或,型的基因类型为,其中,和是显性基因,是隐性基因则下列说法正确的是( )
A. 若父亲的血型为型,则孩子的血型可能为型
B. 若父母的血型不相同,则父母血型的基因类型组合有种
C. 若孩子的爷爷、奶奶、母亲的血型均为型,孩子与父亲血型相同的概率为
D. 若孩子的爷爷、奶奶、母亲的血型均为型,则孩子也是型的概率为
三、填空题:本题共3小题,每小题5分,共15分。
12.若一组样本数据,,,的,则样本数据,,,的方差为______.
13.在一次全运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.羽毛球的比赛规则是局胜制,假设每局比赛甲获胜的概率为,乙获胜的概率为,利用计算机模拟试验,估计甲获得冠军的概率.为此,用计算机产生之间的随机数,当出现随机数,或时,表示一局比赛甲获胜,其概率为由于要比赛三局,所以每个随机数为一组.例如,产生了组随机数:
相当于做了次重复试验,用频率估计甲获得冠军的概率的近似值为 .
14.把正方形沿对角线折成的二面角,、分别是、的中点,是原正方形的中心,则的余弦值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
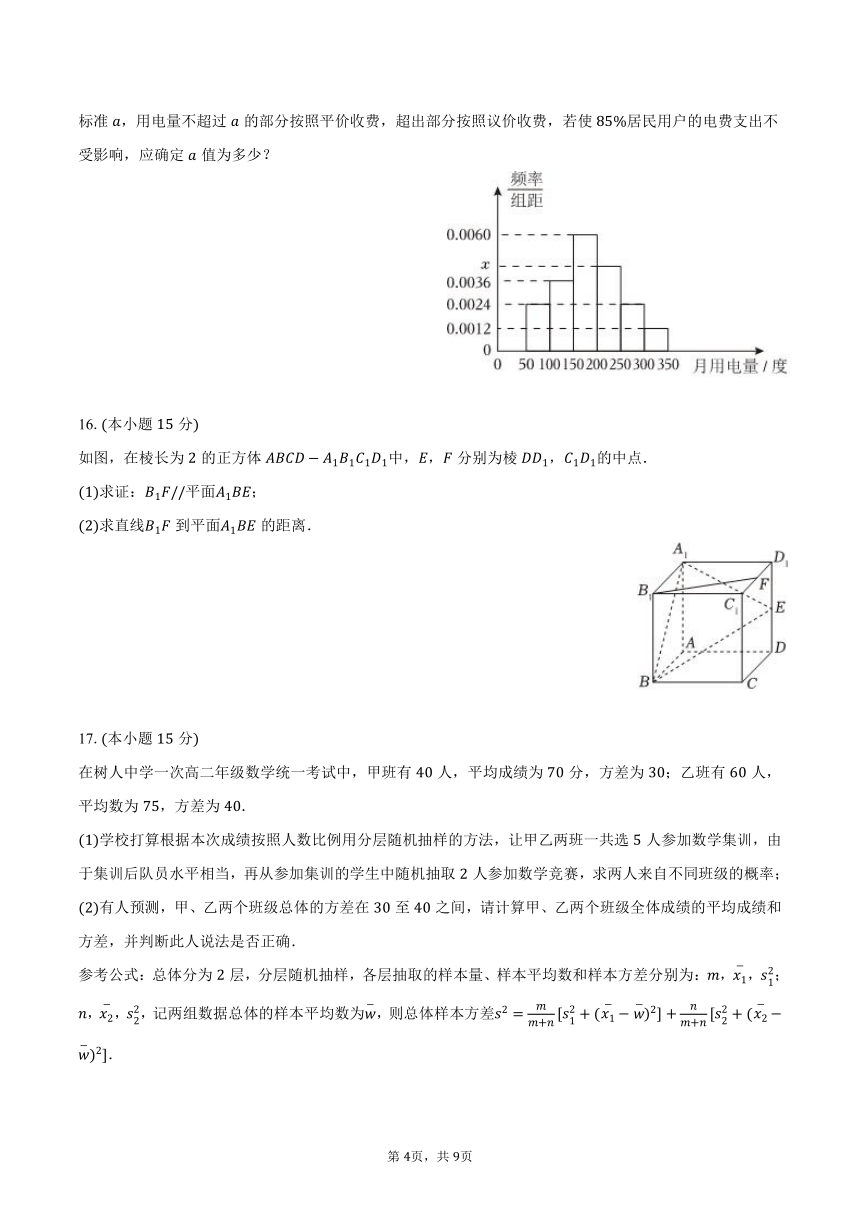
从某小区抽取户居民用户进行月用电量调查,发现他们的用电量都在之间,进行适当分组后每组为左闭右开的区间画出频率分布直方图如图所示.
求频率分布直方图中的值;
政府为了倡议市民节约用电,计划对居民生活用电费用实施阶梯式电价制度,即确定一户居民月用电量标准,用电量不超过的部分按照平价收费,超出部分按照议价收费,若使居民用户的电费支出不受影响,应确定值为多少?
16.本小题分
如图,在棱长为的正方体中,,分别为棱,的中点.
求证:平面;
求直线到平面的距离.
17.本小题分
在树人中学一次高二年级数学统一考试中,甲班有人,平均成绩为分,方差为;乙班有人,平均数为,方差为.
学校打算根据本次成绩按照人数比例用分层随机抽样的方法,让甲乙两班一共选人参加数学集训,由于集训后队员水平相当,再从参加集训的学生中随机抽取人参加数学竞赛,求两人来自不同班级的概率;
有人预测,甲、乙两个班级总体的方差在至之间,请计算甲、乙两个班级全体成绩的平均成绩和方差,并判断此人说法是否正确.
参考公式:总体分为层,分层随机抽样,各层抽取的样本量、样本平均数和样本方差分别为:,,;,,,记两组数据总体的样本平均数为,则总体样本方差.
18.本小题分
如图,在四棱锥中,底面为矩形,底面,,,是的中点,作交于点.
求证:平面;
求的长;
求平面与平面夹角的余弦值.
19.本小题分
单项选择与多项选择题是数学标准化考试中常见题型,单项选择一般从,,,四个选项中选出一个正确答案,其评分标准为全部选对的得分,选错的得分;多项选择题一般从,,,四个选项中选出所有正确的答案四个选项中有两个或三个选项是正确的,其评分标准为全部选对的得分,部分选对的得部分分,有选错的得分.
考生甲有一道单项选择题不会做,他随机选择一个选项,求他猜对本题得分的概率;
考生乙有一道答案为多项选择题不会做,他随机选择两个或三个选项,求他猜对本题得分的概率;
现有道两个正确答案的多项选择题,根据训练经验,每道题考生丙得分的概率为,得分的概率为;考生丁得分的概率为,得分的概率为丙、丁二人答题互不影响,且两题答对与否也互不影响,求这道多项选择题丙丁两位考生总分刚好得分的概率.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:根据题意可得,
解得;
由题意知,要使得居民用户的电费支出不受影响,
即的居民每月的用电量不超过标准度,也即为求该直方图分位数.
因为前个分组频率之和为,
所以分位数在第五组,则有:
,
解得.
16.解:证明:以为原点,,,所在直线分别为,,轴建立如图所示空间直角坐标系,
由题意得,,,,,
所以,,,
设平面的一个法向量为,
则,则,
令,得,,所以,
因为,
所以,
又因为平面,
所以平面;
由可知平面,故求直线到平面的距离可转化为点到平面的距离,
因为,由可知平面的一个法向量为,
设直线到平面的距离为,
则.
17.解:选取的人中,
来自甲班的有人,来自乙班的有人.
记乙班的位学生为,,,甲班的位学生为,,
则从人中任选人,样本空间可记为:
,共包含个样本,
用表示“这人两人来自不同班级”,
则,包含个样本,
故所求概率.
设甲班成绩的平均数为,方差为;乙班成绩的平均数为,方差为,
则,,,,
所以甲、乙两班全部学生的平均成绩为,
两个班级全体成绩的方差为:
故此人的说法是错误的.
18.解:证明:以为原点,,,所在直线分别为,,轴建立如图所示空间直角坐标系.
由题意知:,,,
则,,
,
,
又,,,平面,
平面.
由题意知:,,
设,
则,
,
,
即,
展开有:,
解得:.
故,
则有;
由题意知:,
设平面的法向量,
则,有,则,
令,则,
由知平面,则平面的一个法向量为,
设平面与平面所成的角为,
则,
平面与平面夹角的余弦值为.
19.解:甲同学所有可能的选择答案有,,,共种可能结果,其中正确选项只有一个,
设事件表示“猜对本题得分”,
所以;
乙同学所有可能的选择答案有种:,,,,,,,,,,
设事件表示“猜对本题得分”,
则,有个样本点,
所以;
由题意得丙得分的概率为,丁得分的概率为,
丙丁总分刚好得分的情况包含:
事件:丙得分有一种情况,丁得分有,,三种情况,
则,
事件:丙得分有,两种情况,丁得分有,两种情况,
则,
事件:丙得分有,,三种情况,丁得分有一种情况,
则,
所以丙丁总分刚好得分的概率.
第1页,共1页
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.对总数为的一批零件抽取一个容量为的样本,若每个零件被抽取的概率为,则等于( )
A. B. C. D.
2.已知点是点在坐标平面内的射影,则( )
A. B. C. D.
3.如图,空间四边形中,,,,点在上,且,点为中点,则等于( )
A.
B.
C.
D.
4.甲,乙两人独立地破解同一个谜题,破解出谜题的概率分别为,,则谜题被破解的概率为( )
A. B. C. D.
5.是空气质量的一个重要指标,我国标准采用世卫组织设定的最宽限值,即日均值在以下空气质量为一级,在之间空气质量为二级,在以上空气质量为超标如图是某地月日到日日均值单位:的统计数据,则下列叙述错误的是( )
A. 从这天的日均监测数据中随机抽出一天的数据,空气质量为一级的概率是
B. 从日到日,日均值逐渐降低
C. 这天中日均值的平均数是
D. 这天的日均值的中位数是
6.下列说法正确的是( )
A. 如果一组数据的中位数比平均数小很多,则这组数据是近似对称的
B. 若,,三点不共线,平面外一点,若,则,,,四点共面
C. 已知空间直角坐标系中的三点、、,则点到直线的距离为
D. 有人从一座层大楼的底层进入电梯,假设每个人自第二层开始在每一层离开电梯是等可能的,则该人在不同层离开电梯的概率是
7.如图,平行六面体的所有棱长为,四边形是正方形,,点是与的交点,则直线与所成角的余弦值为( )
A. B. C. D.
8.柜子里有双不同的鞋,从中随机地取出只,记事件“取出的鞋不成双”,事件“取出的鞋都是一只脚的”,事件“取出的鞋子是一只左脚一只右脚的,但不是一双鞋”则有( )
A. B. 与相互独立
C. D. 与互斥
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.北京时间年月日,我国射击健将黄雨婷、盛李豪在奥运会上战胜韩国选手,摘夺了射击混合团体米气步枪金牌,通过赛后数据记录得到其中一名选手的得分分别为,,,,,,,则( )
A. 该组数据的极差为
B. 该组数据的众数为
C. 该组数据的分位数为
D. 若该组数据去掉一个最高分和最低分,则这组数据的方差变小
10.如图,在四面体中,,,,分别是,,,的中点则以下四个结论正确的是( )
A. 向量,,共面
B. 平面
C. 若四面体各棱长均为,则
D. 若是和的交点,则对空间任意一点,有
11.人类的四种血型与基因类型的对应为:型的基因类型为,型的基因类型为或,型的基因类型为或,型的基因类型为,其中,和是显性基因,是隐性基因则下列说法正确的是( )
A. 若父亲的血型为型,则孩子的血型可能为型
B. 若父母的血型不相同,则父母血型的基因类型组合有种
C. 若孩子的爷爷、奶奶、母亲的血型均为型,孩子与父亲血型相同的概率为
D. 若孩子的爷爷、奶奶、母亲的血型均为型,则孩子也是型的概率为
三、填空题:本题共3小题,每小题5分,共15分。
12.若一组样本数据,,,的,则样本数据,,,的方差为______.
13.在一次全运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.羽毛球的比赛规则是局胜制,假设每局比赛甲获胜的概率为,乙获胜的概率为,利用计算机模拟试验,估计甲获得冠军的概率.为此,用计算机产生之间的随机数,当出现随机数,或时,表示一局比赛甲获胜,其概率为由于要比赛三局,所以每个随机数为一组.例如,产生了组随机数:
相当于做了次重复试验,用频率估计甲获得冠军的概率的近似值为 .
14.把正方形沿对角线折成的二面角,、分别是、的中点,是原正方形的中心,则的余弦值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
从某小区抽取户居民用户进行月用电量调查,发现他们的用电量都在之间,进行适当分组后每组为左闭右开的区间画出频率分布直方图如图所示.
求频率分布直方图中的值;
政府为了倡议市民节约用电,计划对居民生活用电费用实施阶梯式电价制度,即确定一户居民月用电量标准,用电量不超过的部分按照平价收费,超出部分按照议价收费,若使居民用户的电费支出不受影响,应确定值为多少?
16.本小题分
如图,在棱长为的正方体中,,分别为棱,的中点.
求证:平面;
求直线到平面的距离.
17.本小题分
在树人中学一次高二年级数学统一考试中,甲班有人,平均成绩为分,方差为;乙班有人,平均数为,方差为.
学校打算根据本次成绩按照人数比例用分层随机抽样的方法,让甲乙两班一共选人参加数学集训,由于集训后队员水平相当,再从参加集训的学生中随机抽取人参加数学竞赛,求两人来自不同班级的概率;
有人预测,甲、乙两个班级总体的方差在至之间,请计算甲、乙两个班级全体成绩的平均成绩和方差,并判断此人说法是否正确.
参考公式:总体分为层,分层随机抽样,各层抽取的样本量、样本平均数和样本方差分别为:,,;,,,记两组数据总体的样本平均数为,则总体样本方差.
18.本小题分
如图,在四棱锥中,底面为矩形,底面,,,是的中点,作交于点.
求证:平面;
求的长;
求平面与平面夹角的余弦值.
19.本小题分
单项选择与多项选择题是数学标准化考试中常见题型,单项选择一般从,,,四个选项中选出一个正确答案,其评分标准为全部选对的得分,选错的得分;多项选择题一般从,,,四个选项中选出所有正确的答案四个选项中有两个或三个选项是正确的,其评分标准为全部选对的得分,部分选对的得部分分,有选错的得分.
考生甲有一道单项选择题不会做,他随机选择一个选项,求他猜对本题得分的概率;
考生乙有一道答案为多项选择题不会做,他随机选择两个或三个选项,求他猜对本题得分的概率;
现有道两个正确答案的多项选择题,根据训练经验,每道题考生丙得分的概率为,得分的概率为;考生丁得分的概率为,得分的概率为丙、丁二人答题互不影响,且两题答对与否也互不影响,求这道多项选择题丙丁两位考生总分刚好得分的概率.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:根据题意可得,
解得;
由题意知,要使得居民用户的电费支出不受影响,
即的居民每月的用电量不超过标准度,也即为求该直方图分位数.
因为前个分组频率之和为,
所以分位数在第五组,则有:
,
解得.
16.解:证明:以为原点,,,所在直线分别为,,轴建立如图所示空间直角坐标系,
由题意得,,,,,
所以,,,
设平面的一个法向量为,
则,则,
令,得,,所以,
因为,
所以,
又因为平面,
所以平面;
由可知平面,故求直线到平面的距离可转化为点到平面的距离,
因为,由可知平面的一个法向量为,
设直线到平面的距离为,
则.
17.解:选取的人中,
来自甲班的有人,来自乙班的有人.
记乙班的位学生为,,,甲班的位学生为,,
则从人中任选人,样本空间可记为:
,共包含个样本,
用表示“这人两人来自不同班级”,
则,包含个样本,
故所求概率.
设甲班成绩的平均数为,方差为;乙班成绩的平均数为,方差为,
则,,,,
所以甲、乙两班全部学生的平均成绩为,
两个班级全体成绩的方差为:
故此人的说法是错误的.
18.解:证明:以为原点,,,所在直线分别为,,轴建立如图所示空间直角坐标系.
由题意知:,,,
则,,
,
,
又,,,平面,
平面.
由题意知:,,
设,
则,
,
,
即,
展开有:,
解得:.
故,
则有;
由题意知:,
设平面的法向量,
则,有,则,
令,则,
由知平面,则平面的一个法向量为,
设平面与平面所成的角为,
则,
平面与平面夹角的余弦值为.
19.解:甲同学所有可能的选择答案有,,,共种可能结果,其中正确选项只有一个,
设事件表示“猜对本题得分”,
所以;
乙同学所有可能的选择答案有种:,,,,,,,,,,
设事件表示“猜对本题得分”,
则,有个样本点,
所以;
由题意得丙得分的概率为,丁得分的概率为,
丙丁总分刚好得分的情况包含:
事件:丙得分有一种情况,丁得分有,,三种情况,
则,
事件:丙得分有,两种情况,丁得分有,两种情况,
则,
事件:丙得分有,,三种情况,丁得分有一种情况,
则,
所以丙丁总分刚好得分的概率.
第1页,共1页
同课章节目录
