2024-2025学年北师大版八年级数学上册期末阶段复习综合模拟测试题(含详细答案)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学上册期末阶段复习综合模拟测试题(含详细答案) |  | |
| 格式 | docx | ||
| 文件大小 | 445.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 23:45:05 | ||
图片预览




文档简介
2024-2025学年北师大版八年级数学上册期末阶段复习综合模拟测试题(附答案)
一、单选题(满分36分)
1.下列命题中,是真命题的是( )
A.的立方根是 B.只有正数才有平方根
C.若,则 D.带根号的数都是无理数
2.下列条件中,不能判断是直角三角形的是( )
A. B.
C. D.
3.小明根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数 中位数 众数 方差
8.3 8.3 8.1 0.15
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A.平均数 B.众数 C.中位数 D.方差
4.已知是二元一次方程组的解,则的值为( )
A. B.2 C. D.4
5.已知点到两坐标轴的距离相等,那么的值为( )
A.4 B. C.或4 D.或
6.某市招聘教师,规定将笔试和面试成绩按照计算总分并择优录取.小星本次参加测试的笔试成绩是80分,面试成绩是90分,则小星最后得分是( )
A.80分 B.85分 C.86分 D.90分
7.在平面直角坐标系中,若将直线向下平移3个单位长度后,恰好经过原点,则直线与x轴的交点坐标( )
A. B. C. D.
8.如图,一棵大树在一次强台风中折断倒下,倒下部分与地面成夹角,倒下后树高还有5米,这棵大树在折断前的高度为( )
A.10米 B.15米 C.25米 D.30米
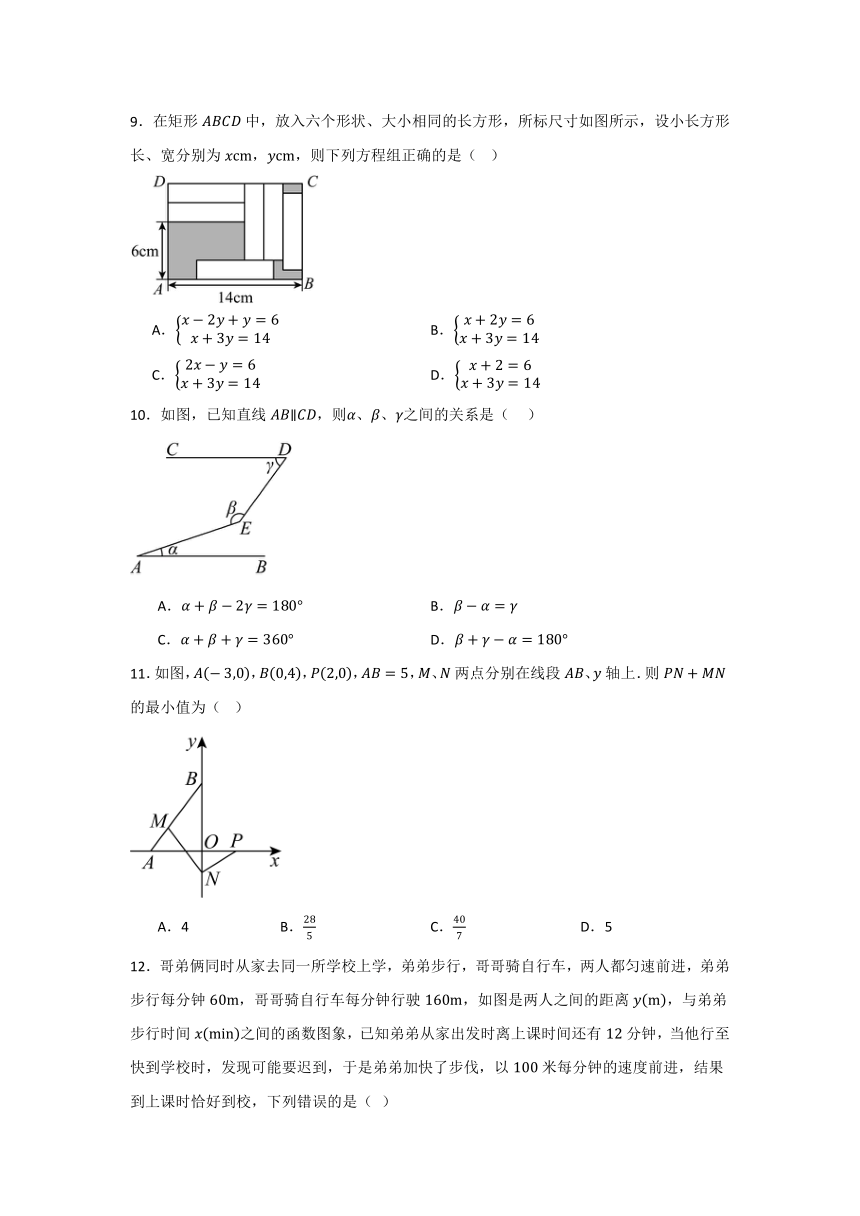
9.在矩形中,放入六个形状、大小相同的长方形,所标尺寸如图所示,设小长方形长、宽分别为,,则下列方程组正确的是( )
A. B.
C. D.
10.如图,已知直线,则、、之间的关系是( )
A. B.
C. D.
11.如图,,,,,、两点分别在线段、轴上.则的最小值为( )
A.4 B. C. D.5
12.哥弟俩同时从家去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进,弟弟步行每分钟,哥哥骑自行车每分钟行驶,如图是两人之间的距离,与弟弟步行时间之间的函数图象,已知弟弟从家出发时离上课时间还有分钟,当他行至快到学校时,发现可能要迟到,于是弟弟加快了步伐,以米每分钟的速度前进,结果到上课时恰好到校,下列错误的是( )
A.点表示哥哥已经到达学校 B.哥哥与弟弟相距的最大距离是米
C.他们家与学校之间的距离为米 D.的函数表达式为
二、填空题(满分24分)
13.已知勾股数的两个数分别是,,则勾股数的第三个数是 .
14.的立方根是 ,的平方根是 ,的绝对值是 .
15.在平面直角坐标系中,若点与点关于x轴对称,则点在第 象限.
16.实数a、b在数轴上的对应点如图所示,化简:的结果是 .
17.一组数据的平均数为5,方差为16,n是正整数,则另一组数据的标准差是 .
18.关于x、y的二元一次方程组的解为,则关于m,n的二元一次方程组的解为 .
19.如图,在中,,平分,若,,则 .
20.如图,直线分别交轴、轴于、两点,在轴的负半轴上有一点,若将沿直线折叠得到,点在轴上,则点的坐标为 .
三、解答题(满分60分)
21.把下列各数填入相应的集合内(填序号):
①,②,③,④,⑤,⑥0,⑦,⑧,⑨…(每相邻两个1之间0的个数逐次加)
(1)无理数集合{ …};
(2)分数集合{ …};
(3)负实数集合{ …}.
22.计算:
(1);
(2).
解方程组:
(3); (4).
23.如图,在中,点D在边上,点G在边上,点E、F在边上,,
(1)试判断与的位置关系,并说明理由;
(2)若,,求的度数.
24.在平面直角坐标系中,的顶点均在格点上.
(1)直接写出A、B、C三点的坐标;
(2)在图中作出关于x轴对称的图形;
(3)在y轴上找一点P,使最短,在图中标出P点的位置,并写出P点的坐标.
25.如图,一个长为15m的梯子斜靠在墙上,梯子的顶端距地面的距离为,
(1)如果梯子的顶端下滑了,那么梯子的底端也向后滑动吗?请通过计算解答.
(2)梯子的顶端从处沿墙下滑的距离与点向外移动的距离有可能相等吗?若有可能,请求出这个距离,没有可能请说明理由.
26.电信诈骗,严重危害着人民群众的财产安全,为提高大家的防范意识,南川区某校举行了主题为“防电信诈骗,保财产安全”的知识竞赛,现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理描述和分析,成绩得分用表示,共分成四组:组,组,组,组,下面给出了部分信息:七年级10名学生的竞赛成绩:84,90,86,99,95,100,89,90,81,96,八年级10名学生的竞赛成绩在组中的数据是:90,94,94,根据信息,解答下列问题:
七八年级抽取的学生竞赛成绩统计表
年级 七年级 八年级
平均数 91 91
中位数 90
众数 100
方差 52 50.4
(1)上述图表中, , , .
(2)根据以上数据,你认为七、八年级哪个年级掌握的相关知识较好?请说明理由(写出一条理由即可);
(3)该校七年级有1600人,八年级有1000人参与此次竞赛,请估计该校七、八两个年级对防电信诈骗意识较强的学生一共有多少人?
27.在中,,点D是射线上一动点(不与点B、C重合),以为边在其右侧作,使得、,连接.
(1)如图①,点D在线段上,求证:.
(2)设.当点D在射线上移动时,探究α与β之间的数量关系,并说明理由.
28.阅读下列材料,然后回答问题.
在进行二次根式化简时,我们有时会碰上如,这样的式子,其实我们还可以将其进一步化简.
(一);
(二);
(三).
类似以上这种化简的步骤叫做分母有理化.
(1)化简:______,______,______,______.
(2)已知:,求的值.
(3)计算:.
29.如图,直线与x轴 y轴分别交于A B两点,在y轴上有一点,动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A B两点的坐标;
(2)求的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时,并求此时M点的坐标.
30.11月5日中国进口博览会如期举行,旨在坚定支持贸易自由化和经济全球化,主动向世界开发市场,吸引了58个“一带一路”沿线国家的超过1000多家企业参展,将成为共建“一带一路”的又一个重要支撑,仅医疗器械及医药保健展区成交57.6亿美元,某保健公司引进了A、B两种型号的医疗器材共计50台,花费2300万美元,已知A型器材每台40万美元,B型器材每台50万美元.
甲(万美元/台) 乙(万美元/台)
A型医疗器材 0.7 1
B型医疗器材 0.8 0.9
(1)求出该公司引进了A、B两种型号的医疗器材各多少台.
(2)现该公司需将购进的医疗器材运往甲、乙两个仓库,已知甲仓库容量为30台,乙仓库容量为20台,运费如表,设运往甲仓库的A型医疗器材为x台(),求总运费为y(万美元)关于x的函数关系式,并求出总运费最低的调运方案,最低总运费是多少万美元.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C D C C A B A D
题号 11 12
答案 A D
1.解:A中,的立方根是,故正确,故选项符合题意;
B中,正数和都有平方根,故错误,故选项不符合题意;
C中,若,则,故错误,故选项不符合题意;
D中,带根号的数不一定是无理数,例如:,是有理数,故错误,故选项不符合题意;
故选:A.
2.解:A、设,则,,
,
是直角三角形,不符合题意;
B、设,则,,
,
解得,
,,,
不是直角三角形,符合题意;
C、,,
,
解得,
是直角三角形,不符合题意;
D、设,则,,
,
是直角三角形,不符合题意;
故选B.
3.解:去掉一个最高分和一个最低分对中位数没有影响,
故选:C.
4.解:把代入方程组,得:,
解得:,
∴;
故选D.
5.解:∵点到两坐标轴的距离相等,
∴
∴或
∴或.
故选C.
6.解:由题意可知,小星最后得分是:(分),
故选:C.
7.解:∵若将一次函数的图象向下平移3个单位长度,
∴平移后的函数解析式为:,
∵函数解的图象经过点,
∴,
解得:,
∴一次函数的解析式为,
当时,,
∴直线与x轴的交点坐标为,
故选:A.
8.解:,
,
,
,
故这棵大树在折断前的高度为米,
故选B.
9.解:依题意,得:.
故选:A.
10.解:过向左作射线,
则,
∴
,
,
,
.
故选:D.
11.解:如图,连接,当、、三点共线,且时,的值最小,最小值是,
,,,
,,
,
,
,
故选:A.
12.解:、∵哥哥的速度始终大于弟弟的速度,
∴在哥哥到达学校前二人之间的距离一直随着时间增大,哥哥到达学校后二人之间的距离随着时间减小,
∴点表示哥哥已经到达学校,
∴原选项正确,不符合题意;
、哥哥与弟弟相距的最大距离是(米),
∴原选项正确,不符合题意;
、他们家与学校之间的距离为(米),
∴原选项正确,不符合题意;
、设坐标,
根据题意,得,
解得,
设的函数表达式为,
将坐标和分别代入,
得,
解得,
∴的函数表达式为,
∴原选项错误,符合题意,
故选:.
13.解:设第三个数为,
∵是一组勾股数,
则 ,
∴,是整数,符合题意;
,
∴,不是整数,不符合题意;
综上可知:勾股数的第三个数是,
故答案为:.
14. 解:∵,
∴的立方根是;
的平方根是;
∵
∴
∴
∴,
∴的绝对值是.
故答案为:,,.
15.解:点与点关于轴对称,
,
解得,
点在第三象限.
故答案为:三.
16.解:如图所示:,
∴
,
故答案为:.
17.解:根据题意,数据的平均数为5,方差为16,
即,
,
则的平均数
,
另一组数据的方差
,
∴标准差.
故答案为:12.
18.解:关于x、y的二元一次方程组的解为,
关于、的二元一次方程组的解是,
解得,
关于m,n的二元一次方程组的解为,
故答案为:.
19.解:∵平分交于点E,
∴,
∵,
∴,
∵在中,于点D,
∴,
在中,∵,
∴
.
∵是的一个外角,
∴,
∴,
故答案为:35.
20.解:直线分别交轴、轴于、两点,
,,则
,
由题意得:,
,
故点,
设点的坐标为:,
,
解得:,
故点 .
故答案为:.
21.解:(1)由题知,,
∴无理数集合{②,③,⑦,⑨…};
(2)分数集合{①,④,⑧…};
(3)负实数集合{①,②,⑦,⑧…}.
22.(1)解:
;
(2)解:
.
(3)解:,
,得,
解得,
把代入①,得,
解得,
所以方程组的解为;
(4)解:,
整理①得,即,
所以整理②得,
把代入,
得,
解得,
把代入,
解得,
所以方程组的解为.
23.(1)解:,理由如下:
∵,
∴,
∴,
又,
∴,
∴;
(2)解:∵,
∴,
,
,
∴.
24.(1)解:由平面直角坐标系可得,,,.
(2)如图所示,即为所求;
(3)如图,作点A关于轴对称点,连接交轴于P点,
根据轴对称的性质可知,
,
由两点之间线段最短可知,当点在线段上时,最短,
如图,P点的位置即为所求;
点A关于轴对称点为,,
,
设直线的解析式为,
代入和得,,
解得:,
直线的解析式为,
令,则,
P点的坐标为.
25.(1)解:如果梯子的顶端下滑了,那么梯子的底端不是向后滑动,理由如下:
在中,,,
由勾股定理得:,
在中,,,
由勾股定理得:,
,
如果梯子的顶端下滑了,那么梯子的底端不是向后滑动;
(2)解:梯子的顶端从处沿墙下滑的距离与点向外移动的距离有可能相等,理由如下:
由(1)可知,,
设梯子顶端从处沿墙下滑的距离为, 则,,
在中,由勾股定理得:,即,
解得:,(不符合题意,舍去),
所以,当梯子的顶端从处沿墙下滑的距离是时,与点向外移动的距离有可能相等.
26.解:(1)将七年级10名学生的竞赛成绩重新排列为:81,84,86,89,90,90,95,96,99,100,
90出现次数最多,所以众数为;
八年级学生的竞赛成绩C组有3人,所以C组占总数抽取人数的,
可知,
所以;
八年级学生竞赛成绩的中位数是第5个,第6个数的平均数,即为94,94的平均数,
所以中位数.
故答案为:90,94,40;
(2)八年级掌握的相关知识较好,理由如下:
因为两个年级的平均数均为91,但八年级的中位数94大于七年级的中位数90,所以八年级掌握的相关知识较好;
(3).
答:该校七八两个年级对防电信诈骗意识较强的学生一共有1660人.
27.(1)证明:∵,
∴,
∴,
∵,
∴;
(2)解:当点D在射线上移动时,或,理由如下:
①当点D在线段上移动时,
由(1)可知:,
∴,
∴,
∵,
∴,即;
②当点D在的延长线上时,
同理,,
∴,
∵,
∴,
∴,即.
28.(1)解:,
,
,
,
故答案为:;
(2)解:,
,
;
(3)解:
.
29.(1)解:令得,
;
令得,
.
(2)解:∵动点M从A点以每秒1个单位的速度沿x轴向左移动,
,
,
即的面积S与M的移动时间t之间的函数关系式为:.
(3)解:因为,
.
若,则,
,
解得或.
当;
当.
当或时,
此时M点的坐标.
30.解:(1)设该公司引进a台A型号医疗器材,则引进B型号器材b台,根据题意得:
,
解得:,
答:该公司引进20台A型号医疗器材,30台B型号医疗器材.
(2)依题意得,运往甲仓库的B型医疗器材为台,运往乙仓库的A型为台,运往乙仓库的B型为x台,
∴,
整理得:,
∴y随x的增大而减小,
∵,
∴当时,y有最小值,最小值为,
答:y与x的函数关系式为;总运费最低的调运方案为:运往甲仓库的A型医疗器材为15台,运往甲仓库的B型医疗器材为15台,运往乙仓库的A型医疗器材为5台,运往乙仓库的B型医疗器材为15台;最低总运费为41万美元.
一、单选题(满分36分)
1.下列命题中,是真命题的是( )
A.的立方根是 B.只有正数才有平方根
C.若,则 D.带根号的数都是无理数
2.下列条件中,不能判断是直角三角形的是( )
A. B.
C. D.
3.小明根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数 中位数 众数 方差
8.3 8.3 8.1 0.15
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A.平均数 B.众数 C.中位数 D.方差
4.已知是二元一次方程组的解,则的值为( )
A. B.2 C. D.4
5.已知点到两坐标轴的距离相等,那么的值为( )
A.4 B. C.或4 D.或
6.某市招聘教师,规定将笔试和面试成绩按照计算总分并择优录取.小星本次参加测试的笔试成绩是80分,面试成绩是90分,则小星最后得分是( )
A.80分 B.85分 C.86分 D.90分
7.在平面直角坐标系中,若将直线向下平移3个单位长度后,恰好经过原点,则直线与x轴的交点坐标( )
A. B. C. D.
8.如图,一棵大树在一次强台风中折断倒下,倒下部分与地面成夹角,倒下后树高还有5米,这棵大树在折断前的高度为( )
A.10米 B.15米 C.25米 D.30米
9.在矩形中,放入六个形状、大小相同的长方形,所标尺寸如图所示,设小长方形长、宽分别为,,则下列方程组正确的是( )
A. B.
C. D.
10.如图,已知直线,则、、之间的关系是( )
A. B.
C. D.
11.如图,,,,,、两点分别在线段、轴上.则的最小值为( )
A.4 B. C. D.5
12.哥弟俩同时从家去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进,弟弟步行每分钟,哥哥骑自行车每分钟行驶,如图是两人之间的距离,与弟弟步行时间之间的函数图象,已知弟弟从家出发时离上课时间还有分钟,当他行至快到学校时,发现可能要迟到,于是弟弟加快了步伐,以米每分钟的速度前进,结果到上课时恰好到校,下列错误的是( )
A.点表示哥哥已经到达学校 B.哥哥与弟弟相距的最大距离是米
C.他们家与学校之间的距离为米 D.的函数表达式为
二、填空题(满分24分)
13.已知勾股数的两个数分别是,,则勾股数的第三个数是 .
14.的立方根是 ,的平方根是 ,的绝对值是 .
15.在平面直角坐标系中,若点与点关于x轴对称,则点在第 象限.
16.实数a、b在数轴上的对应点如图所示,化简:的结果是 .
17.一组数据的平均数为5,方差为16,n是正整数,则另一组数据的标准差是 .
18.关于x、y的二元一次方程组的解为,则关于m,n的二元一次方程组的解为 .
19.如图,在中,,平分,若,,则 .
20.如图,直线分别交轴、轴于、两点,在轴的负半轴上有一点,若将沿直线折叠得到,点在轴上,则点的坐标为 .
三、解答题(满分60分)
21.把下列各数填入相应的集合内(填序号):
①,②,③,④,⑤,⑥0,⑦,⑧,⑨…(每相邻两个1之间0的个数逐次加)
(1)无理数集合{ …};
(2)分数集合{ …};
(3)负实数集合{ …}.
22.计算:
(1);
(2).
解方程组:
(3); (4).
23.如图,在中,点D在边上,点G在边上,点E、F在边上,,
(1)试判断与的位置关系,并说明理由;
(2)若,,求的度数.
24.在平面直角坐标系中,的顶点均在格点上.
(1)直接写出A、B、C三点的坐标;
(2)在图中作出关于x轴对称的图形;
(3)在y轴上找一点P,使最短,在图中标出P点的位置,并写出P点的坐标.
25.如图,一个长为15m的梯子斜靠在墙上,梯子的顶端距地面的距离为,
(1)如果梯子的顶端下滑了,那么梯子的底端也向后滑动吗?请通过计算解答.
(2)梯子的顶端从处沿墙下滑的距离与点向外移动的距离有可能相等吗?若有可能,请求出这个距离,没有可能请说明理由.
26.电信诈骗,严重危害着人民群众的财产安全,为提高大家的防范意识,南川区某校举行了主题为“防电信诈骗,保财产安全”的知识竞赛,现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理描述和分析,成绩得分用表示,共分成四组:组,组,组,组,下面给出了部分信息:七年级10名学生的竞赛成绩:84,90,86,99,95,100,89,90,81,96,八年级10名学生的竞赛成绩在组中的数据是:90,94,94,根据信息,解答下列问题:
七八年级抽取的学生竞赛成绩统计表
年级 七年级 八年级
平均数 91 91
中位数 90
众数 100
方差 52 50.4
(1)上述图表中, , , .
(2)根据以上数据,你认为七、八年级哪个年级掌握的相关知识较好?请说明理由(写出一条理由即可);
(3)该校七年级有1600人,八年级有1000人参与此次竞赛,请估计该校七、八两个年级对防电信诈骗意识较强的学生一共有多少人?
27.在中,,点D是射线上一动点(不与点B、C重合),以为边在其右侧作,使得、,连接.
(1)如图①,点D在线段上,求证:.
(2)设.当点D在射线上移动时,探究α与β之间的数量关系,并说明理由.
28.阅读下列材料,然后回答问题.
在进行二次根式化简时,我们有时会碰上如,这样的式子,其实我们还可以将其进一步化简.
(一);
(二);
(三).
类似以上这种化简的步骤叫做分母有理化.
(1)化简:______,______,______,______.
(2)已知:,求的值.
(3)计算:.
29.如图,直线与x轴 y轴分别交于A B两点,在y轴上有一点,动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A B两点的坐标;
(2)求的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时,并求此时M点的坐标.
30.11月5日中国进口博览会如期举行,旨在坚定支持贸易自由化和经济全球化,主动向世界开发市场,吸引了58个“一带一路”沿线国家的超过1000多家企业参展,将成为共建“一带一路”的又一个重要支撑,仅医疗器械及医药保健展区成交57.6亿美元,某保健公司引进了A、B两种型号的医疗器材共计50台,花费2300万美元,已知A型器材每台40万美元,B型器材每台50万美元.
甲(万美元/台) 乙(万美元/台)
A型医疗器材 0.7 1
B型医疗器材 0.8 0.9
(1)求出该公司引进了A、B两种型号的医疗器材各多少台.
(2)现该公司需将购进的医疗器材运往甲、乙两个仓库,已知甲仓库容量为30台,乙仓库容量为20台,运费如表,设运往甲仓库的A型医疗器材为x台(),求总运费为y(万美元)关于x的函数关系式,并求出总运费最低的调运方案,最低总运费是多少万美元.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C D C C A B A D
题号 11 12
答案 A D
1.解:A中,的立方根是,故正确,故选项符合题意;
B中,正数和都有平方根,故错误,故选项不符合题意;
C中,若,则,故错误,故选项不符合题意;
D中,带根号的数不一定是无理数,例如:,是有理数,故错误,故选项不符合题意;
故选:A.
2.解:A、设,则,,
,
是直角三角形,不符合题意;
B、设,则,,
,
解得,
,,,
不是直角三角形,符合题意;
C、,,
,
解得,
是直角三角形,不符合题意;
D、设,则,,
,
是直角三角形,不符合题意;
故选B.
3.解:去掉一个最高分和一个最低分对中位数没有影响,
故选:C.
4.解:把代入方程组,得:,
解得:,
∴;
故选D.
5.解:∵点到两坐标轴的距离相等,
∴
∴或
∴或.
故选C.
6.解:由题意可知,小星最后得分是:(分),
故选:C.
7.解:∵若将一次函数的图象向下平移3个单位长度,
∴平移后的函数解析式为:,
∵函数解的图象经过点,
∴,
解得:,
∴一次函数的解析式为,
当时,,
∴直线与x轴的交点坐标为,
故选:A.
8.解:,
,
,
,
故这棵大树在折断前的高度为米,
故选B.
9.解:依题意,得:.
故选:A.
10.解:过向左作射线,
则,
∴
,
,
,
.
故选:D.
11.解:如图,连接,当、、三点共线,且时,的值最小,最小值是,
,,,
,,
,
,
,
故选:A.
12.解:、∵哥哥的速度始终大于弟弟的速度,
∴在哥哥到达学校前二人之间的距离一直随着时间增大,哥哥到达学校后二人之间的距离随着时间减小,
∴点表示哥哥已经到达学校,
∴原选项正确,不符合题意;
、哥哥与弟弟相距的最大距离是(米),
∴原选项正确,不符合题意;
、他们家与学校之间的距离为(米),
∴原选项正确,不符合题意;
、设坐标,
根据题意,得,
解得,
设的函数表达式为,
将坐标和分别代入,
得,
解得,
∴的函数表达式为,
∴原选项错误,符合题意,
故选:.
13.解:设第三个数为,
∵是一组勾股数,
则 ,
∴,是整数,符合题意;
,
∴,不是整数,不符合题意;
综上可知:勾股数的第三个数是,
故答案为:.
14. 解:∵,
∴的立方根是;
的平方根是;
∵
∴
∴
∴,
∴的绝对值是.
故答案为:,,.
15.解:点与点关于轴对称,
,
解得,
点在第三象限.
故答案为:三.
16.解:如图所示:,
∴
,
故答案为:.
17.解:根据题意,数据的平均数为5,方差为16,
即,
,
则的平均数
,
另一组数据的方差
,
∴标准差.
故答案为:12.
18.解:关于x、y的二元一次方程组的解为,
关于、的二元一次方程组的解是,
解得,
关于m,n的二元一次方程组的解为,
故答案为:.
19.解:∵平分交于点E,
∴,
∵,
∴,
∵在中,于点D,
∴,
在中,∵,
∴
.
∵是的一个外角,
∴,
∴,
故答案为:35.
20.解:直线分别交轴、轴于、两点,
,,则
,
由题意得:,
,
故点,
设点的坐标为:,
,
解得:,
故点 .
故答案为:.
21.解:(1)由题知,,
∴无理数集合{②,③,⑦,⑨…};
(2)分数集合{①,④,⑧…};
(3)负实数集合{①,②,⑦,⑧…}.
22.(1)解:
;
(2)解:
.
(3)解:,
,得,
解得,
把代入①,得,
解得,
所以方程组的解为;
(4)解:,
整理①得,即,
所以整理②得,
把代入,
得,
解得,
把代入,
解得,
所以方程组的解为.
23.(1)解:,理由如下:
∵,
∴,
∴,
又,
∴,
∴;
(2)解:∵,
∴,
,
,
∴.
24.(1)解:由平面直角坐标系可得,,,.
(2)如图所示,即为所求;
(3)如图,作点A关于轴对称点,连接交轴于P点,
根据轴对称的性质可知,
,
由两点之间线段最短可知,当点在线段上时,最短,
如图,P点的位置即为所求;
点A关于轴对称点为,,
,
设直线的解析式为,
代入和得,,
解得:,
直线的解析式为,
令,则,
P点的坐标为.
25.(1)解:如果梯子的顶端下滑了,那么梯子的底端不是向后滑动,理由如下:
在中,,,
由勾股定理得:,
在中,,,
由勾股定理得:,
,
如果梯子的顶端下滑了,那么梯子的底端不是向后滑动;
(2)解:梯子的顶端从处沿墙下滑的距离与点向外移动的距离有可能相等,理由如下:
由(1)可知,,
设梯子顶端从处沿墙下滑的距离为, 则,,
在中,由勾股定理得:,即,
解得:,(不符合题意,舍去),
所以,当梯子的顶端从处沿墙下滑的距离是时,与点向外移动的距离有可能相等.
26.解:(1)将七年级10名学生的竞赛成绩重新排列为:81,84,86,89,90,90,95,96,99,100,
90出现次数最多,所以众数为;
八年级学生的竞赛成绩C组有3人,所以C组占总数抽取人数的,
可知,
所以;
八年级学生竞赛成绩的中位数是第5个,第6个数的平均数,即为94,94的平均数,
所以中位数.
故答案为:90,94,40;
(2)八年级掌握的相关知识较好,理由如下:
因为两个年级的平均数均为91,但八年级的中位数94大于七年级的中位数90,所以八年级掌握的相关知识较好;
(3).
答:该校七八两个年级对防电信诈骗意识较强的学生一共有1660人.
27.(1)证明:∵,
∴,
∴,
∵,
∴;
(2)解:当点D在射线上移动时,或,理由如下:
①当点D在线段上移动时,
由(1)可知:,
∴,
∴,
∵,
∴,即;
②当点D在的延长线上时,
同理,,
∴,
∵,
∴,
∴,即.
28.(1)解:,
,
,
,
故答案为:;
(2)解:,
,
;
(3)解:
.
29.(1)解:令得,
;
令得,
.
(2)解:∵动点M从A点以每秒1个单位的速度沿x轴向左移动,
,
,
即的面积S与M的移动时间t之间的函数关系式为:.
(3)解:因为,
.
若,则,
,
解得或.
当;
当.
当或时,
此时M点的坐标.
30.解:(1)设该公司引进a台A型号医疗器材,则引进B型号器材b台,根据题意得:
,
解得:,
答:该公司引进20台A型号医疗器材,30台B型号医疗器材.
(2)依题意得,运往甲仓库的B型医疗器材为台,运往乙仓库的A型为台,运往乙仓库的B型为x台,
∴,
整理得:,
∴y随x的增大而减小,
∵,
∴当时,y有最小值,最小值为,
答:y与x的函数关系式为;总运费最低的调运方案为:运往甲仓库的A型医疗器材为15台,运往甲仓库的B型医疗器材为15台,运往乙仓库的A型医疗器材为5台,运往乙仓库的B型医疗器材为15台;最低总运费为41万美元.
同课章节目录
