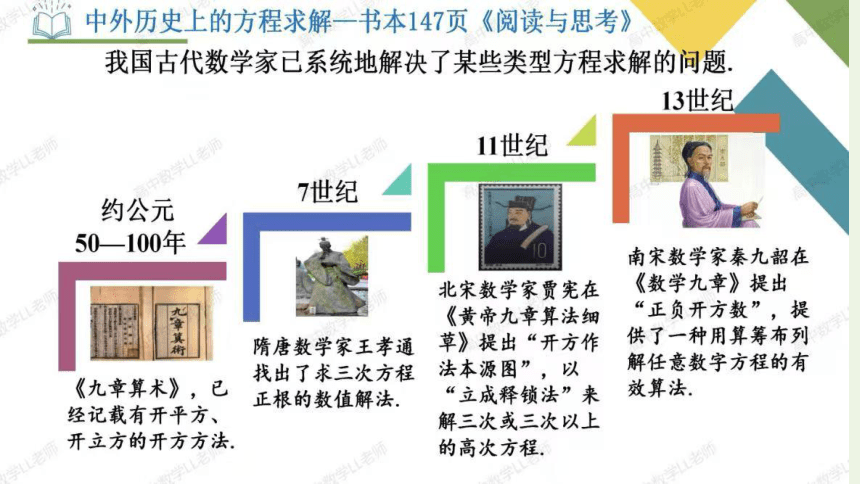
8.1.1函数的零点 课件(共19张PPT)-2024-2025学年高一上学期数学苏教版(2019)必修第一册
文档属性
| 名称 | 8.1.1函数的零点 课件(共19张PPT)-2024-2025学年高一上学期数学苏教版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 18:52:09 | ||
图片预览





文档简介
(共19张PPT)
8.1.1 函 数 的 零 点
苏教版高中数学必修第一册
学习
目标
一
结合二次函数的零点,了解函数零点与方程关系。
二
了解具体二次函数 及其图象,掌握函数零点存在性定理。
三
体会并理解函数与方程的相互转化的数学思想。
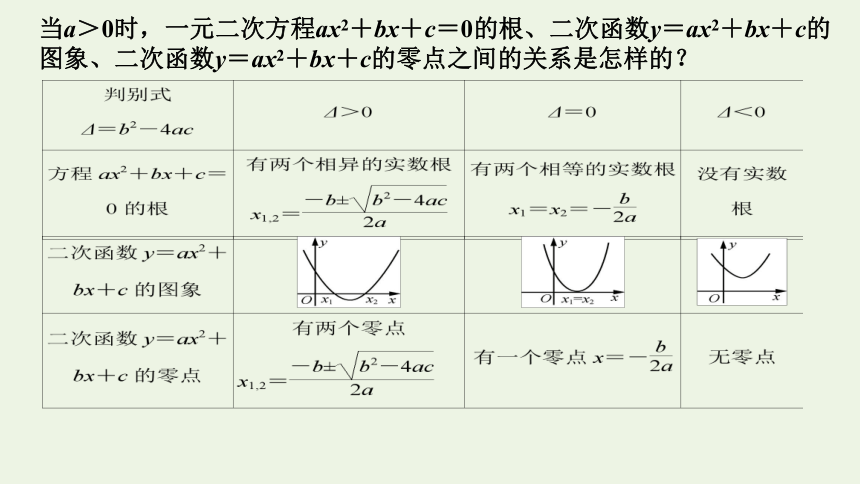
当a>0时,一元二次方程ax2+bx+c=0的根、二次函数y=ax2+bx+c的
图象、二次函数y=ax2+bx+c的零点之间的关系是怎样的?
方程f(x)=0 方程f(x)=0的 实数解 函数y=f(x)的零点
x-2=0
x +1=0
2x=0
x=2
2
x=-1
-1
x=0
0
活动一
函数零点的定义
注:函数的零点是实数,不是点。在写零点时一定是一个数,而不是一个坐标。
活动一
函数零点的定义
(完成导学单思考1)
活动二
函数零点、方程的根与图象公共点的关系
探究1:方程x -2x=0的实数解是多少?
探究2 :函数f(x)=x -2x的零点是多少?
探究3:函数f(x)=x -2x的图像与x轴交点的横坐标是多少?
解析:x =0 x =2
解析:0 、 2
解析:x =0 x =2
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
方程f(x)=0有实数解
转
化
关
系
数
形
(完成导学单思考2)
活动二
函数零点存在性定理
(1)在[2,3]上,我们发现在区间(2,3)内有
,有f(2) 0, f(3) 0,得到f(2) f(3) 0 (填>或<)
同样地
(2)在[-1,0]上,我们发现函数f(x)区间(-1,0)内有
,有f(-1) 0, f(0) 0,得到f(-1) f(0) 0 (填>或<)
零点
>
<
<
零点
>
<
<
在零点附近,图像“穿过”x轴,左右两侧的函数值总是异号
活动二
函数零点存在性定理
探究4:猜想正确吗? 若函数y=f(x)在区间[a,b]有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点吗?
活动二
函数零点存在性定理
活动二
函数零点存在性定理
若函数y=f(x)在区间[a,b]上的图象是一条 的曲线,且 ,则函数y=f(x)在区间(a,b) 上至少有一个零点。即存在c∈(a,b),使得 ,这个c也就是方程 f(x)=0的解。
不间断
f(a) f(b)<0
f(c) =0
函数零点存在定理:
活动二
函数零点存在性定理
函数y=f(x)在区间(a,b)上有零点,但不一定有f(a)·f(b)<0.
也就是说上述定理不可逆.
(完成导学单思考5)
活动二
函数零点存在性定理
(完成导学单思考6)
活动三
判断零点是否存在
跟踪训练
当堂检测
1.已知函数 f(x)为奇函数,且该函数有三个零点,则三个零点之和等于( )
A.0 B.1 C.-1 D.-1
2.根据表格中的数据,可以判断方程 e 一(n+2)=0(e≈2.72)的一个根所在的区间是( )
n -1 0 1 2 3
e 0.37 1 2.72 7.40 20.12
n+2 1 2 3 4 5
A.(-1,0) B. (0,1) C.(1,2) D.(2,3)
下课了
布置作业
活动单49页例1
活动单50页思考4,5,6。
8.1.1 函 数 的 零 点
苏教版高中数学必修第一册
学习
目标
一
结合二次函数的零点,了解函数零点与方程关系。
二
了解具体二次函数 及其图象,掌握函数零点存在性定理。
三
体会并理解函数与方程的相互转化的数学思想。
当a>0时,一元二次方程ax2+bx+c=0的根、二次函数y=ax2+bx+c的
图象、二次函数y=ax2+bx+c的零点之间的关系是怎样的?
方程f(x)=0 方程f(x)=0的 实数解 函数y=f(x)的零点
x-2=0
x +1=0
2x=0
x=2
2
x=-1
-1
x=0
0
活动一
函数零点的定义
注:函数的零点是实数,不是点。在写零点时一定是一个数,而不是一个坐标。
活动一
函数零点的定义
(完成导学单思考1)
活动二
函数零点、方程的根与图象公共点的关系
探究1:方程x -2x=0的实数解是多少?
探究2 :函数f(x)=x -2x的零点是多少?
探究3:函数f(x)=x -2x的图像与x轴交点的横坐标是多少?
解析:x =0 x =2
解析:0 、 2
解析:x =0 x =2
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
方程f(x)=0有实数解
转
化
关
系
数
形
(完成导学单思考2)
活动二
函数零点存在性定理
(1)在[2,3]上,我们发现在区间(2,3)内有
,有f(2) 0, f(3) 0,得到f(2) f(3) 0 (填>或<)
同样地
(2)在[-1,0]上,我们发现函数f(x)区间(-1,0)内有
,有f(-1) 0, f(0) 0,得到f(-1) f(0) 0 (填>或<)
零点
>
<
<
零点
>
<
<
在零点附近,图像“穿过”x轴,左右两侧的函数值总是异号
活动二
函数零点存在性定理
探究4:猜想正确吗? 若函数y=f(x)在区间[a,b]有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点吗?
活动二
函数零点存在性定理
活动二
函数零点存在性定理
若函数y=f(x)在区间[a,b]上的图象是一条 的曲线,且 ,则函数y=f(x)在区间(a,b) 上至少有一个零点。即存在c∈(a,b),使得 ,这个c也就是方程 f(x)=0的解。
不间断
f(a) f(b)<0
f(c) =0
函数零点存在定理:
活动二
函数零点存在性定理
函数y=f(x)在区间(a,b)上有零点,但不一定有f(a)·f(b)<0.
也就是说上述定理不可逆.
(完成导学单思考5)
活动二
函数零点存在性定理
(完成导学单思考6)
活动三
判断零点是否存在
跟踪训练
当堂检测
1.已知函数 f(x)为奇函数,且该函数有三个零点,则三个零点之和等于( )
A.0 B.1 C.-1 D.-1
2.根据表格中的数据,可以判断方程 e 一(n+2)=0(e≈2.72)的一个根所在的区间是( )
n -1 0 1 2 3
e 0.37 1 2.72 7.40 20.12
n+2 1 2 3 4 5
A.(-1,0) B. (0,1) C.(1,2) D.(2,3)
下课了
布置作业
活动单49页例1
活动单50页思考4,5,6。
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
