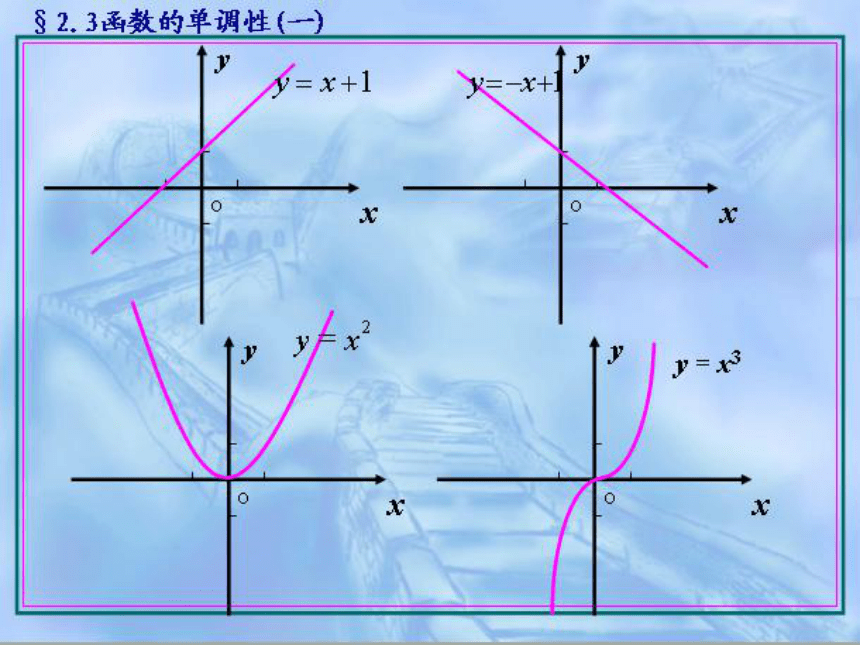
2.1.3函数的单调性
图片预览







文档简介
课件23张PPT。2.1.3函数的单调性 建立函数的目的是研究函数值与自变量的关系,自变量的变化对函数值变化的影响是经常受到关注的问题.例如水位的涨落随时间变化的规律,是防涝抗旱工作中必须解决的实际问题.下面我们通过一组图像,开始研究函数在这方面的一个主要性质——函数的单调性. 在函数y=f(x)的图象上任取两点A(x1, y1),B(x2, y2),记
△x=x2-x1,△y=f(x2)-f(x1)=y2-y1,
△x表示自变量x的改变量,△y表示因变量y的改变量. 当△y=f(x2) -f(x1)<0时,就称y=f(x)在区间M上是减函数.1、增函数与减函数定义⒉ 单调性与单调区间 在单调区间上,增函数的图象是上升的,减函数的图象是下降的. 若函数y=f(x)在某个区间是增函数或减函数,则就说函数y=f(x)在这一区间具有(严格的)单调性, 这一区间叫做函数y=f(x)的单调区间.此时也说函数y=f(x)是这一区间上的单调函数.注意:①函数的单调性是相对某个区间而言,
不能直接说某函数是增函数或减函数。②讨论函数的单调性和书写函数的
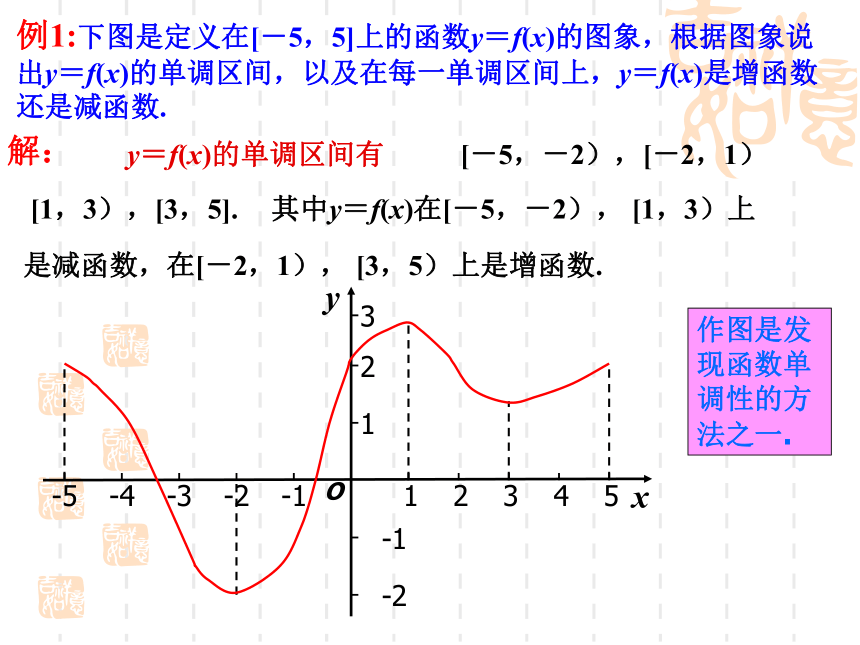
单调区间是两个不同的问题。③函数的单调区间是其定义域上的子集. 函数f(x)在给定区间上为增函数。如何描述函数f(x)的单调性呢? 函数f (x)在给定区间上为减函数。例1:下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,y=f(x)是增函数还是减函数.解:y=f(x)的单调区间有[-5,-2),[-2,1)[1,3),[3,5].其中y=f(x)在[-5,-2), [1,3)上是减函数,在[-2,1), [3,5)上是增函数.作图是发现函数单调性的方法之一.单调递增区间:单调递减区间:证明:(设条件)(论证结果)(下结论)证明:设x1,x2∈(0,+∞),且x1<x2,则f(x)在定义域 上是减函数吗?
减函数
取x1=-1,x2=1 f(-1)=-1 f(1)=1 -1<1 f(-1)<f(1)证明:f(x1)-f(x2)=(3x1+2)-(3x2+2)
=3(x1-x2)由x1<x2,得 x1-x2<0设x1,x2是R上的任意两个实数,且x1<x2,则思考:判断函数f(x)=x2+1在(0,+∞)上
是增函数还是减函数?并给予证明。解:函数f(x)=x2+1在(0,+∞)上是增函数.下面给予证明:设x1,x2∈(0,+∞),且x1<x2∴ 函数f(x)=x2+1在(0,+∞)上是增函数.x1x2y1y2x2x1y1y2小结:函数单调性简单性质总结②函数f(x)和g(x)在区间I上为增(减)函数,
则f(x)+g(x)在I上为增(减)函数。③函数f(x)和g(x)在区间I上分别为增函数和减函数,
则f(x)-g(x)在I上为增函数。
④函数f(x)和g(x)在区间I上为增(减)函数,且 f(x)>0,g(x)>0,则f(x)g(x)在I上为增(减)函数。①函数y=f(x) 在区间I上为增(减)函数,则
函数y=af(x)+b (a>0)在区间I上为增(减)函数补充练习:1、已知二次函数f(x)=ax2+bx+c (a>0)满足f(2+t)=f(2-t),试比较f(1)、f(2)、f(4)的大小.f(4)>f(1)>f(2)2、函数y=x2+bx+c在[0,+∞)上是单调函数的充分必要条件是( ).
(A) b≥0 (B) b≤0 (C ) b>0 (D) b<0A 当x≥0时, f(x)=-x2+2x+3,对称轴为x=1,抛物线开口向下,所以x∈[0,1]时,f(x)为增函数;x∈[1,+∞)时,f(x)为减函数; 当x<0时, f(x)=-x2-2x+3,对称轴为x=-1,抛物线开口向下,所以x∈[-∞,-1]时,f(x)为增函数;x∈[-1,0]时,f(x)为减函数;
△x=x2-x1,△y=f(x2)-f(x1)=y2-y1,
△x表示自变量x的改变量,△y表示因变量y的改变量. 当△y=f(x2) -f(x1)<0时,就称y=f(x)在区间M上是减函数.1、增函数与减函数定义⒉ 单调性与单调区间 在单调区间上,增函数的图象是上升的,减函数的图象是下降的. 若函数y=f(x)在某个区间是增函数或减函数,则就说函数y=f(x)在这一区间具有(严格的)单调性, 这一区间叫做函数y=f(x)的单调区间.此时也说函数y=f(x)是这一区间上的单调函数.注意:①函数的单调性是相对某个区间而言,
不能直接说某函数是增函数或减函数。②讨论函数的单调性和书写函数的
单调区间是两个不同的问题。③函数的单调区间是其定义域上的子集. 函数f(x)在给定区间上为增函数。如何描述函数f(x)的单调性呢? 函数f (x)在给定区间上为减函数。例1:下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,y=f(x)是增函数还是减函数.解:y=f(x)的单调区间有[-5,-2),[-2,1)[1,3),[3,5].其中y=f(x)在[-5,-2), [1,3)上是减函数,在[-2,1), [3,5)上是增函数.作图是发现函数单调性的方法之一.单调递增区间:单调递减区间:证明:(设条件)(论证结果)(下结论)证明:设x1,x2∈(0,+∞),且x1<x2,则f(x)在定义域 上是减函数吗?
减函数
取x1=-1,x2=1 f(-1)=-1 f(1)=1 -1<1 f(-1)<f(1)证明:f(x1)-f(x2)=(3x1+2)-(3x2+2)
=3(x1-x2)由x1<x2,得 x1-x2<0设x1,x2是R上的任意两个实数,且x1<x2,则思考:判断函数f(x)=x2+1在(0,+∞)上
是增函数还是减函数?并给予证明。解:函数f(x)=x2+1在(0,+∞)上是增函数.下面给予证明:设x1,x2∈(0,+∞),且x1<x2∴ 函数f(x)=x2+1在(0,+∞)上是增函数.x1x2y1y2x2x1y1y2小结:函数单调性简单性质总结②函数f(x)和g(x)在区间I上为增(减)函数,
则f(x)+g(x)在I上为增(减)函数。③函数f(x)和g(x)在区间I上分别为增函数和减函数,
则f(x)-g(x)在I上为增函数。
④函数f(x)和g(x)在区间I上为增(减)函数,且 f(x)>0,g(x)>0,则f(x)g(x)在I上为增(减)函数。①函数y=f(x) 在区间I上为增(减)函数,则
函数y=af(x)+b (a>0)在区间I上为增(减)函数补充练习:1、已知二次函数f(x)=ax2+bx+c (a>0)满足f(2+t)=f(2-t),试比较f(1)、f(2)、f(4)的大小.f(4)>f(1)>f(2)2、函数y=x2+bx+c在[0,+∞)上是单调函数的充分必要条件是( ).
(A) b≥0 (B) b≤0 (C ) b>0 (D) b<0A 当x≥0时, f(x)=-x2+2x+3,对称轴为x=1,抛物线开口向下,所以x∈[0,1]时,f(x)为增函数;x∈[1,+∞)时,f(x)为减函数; 当x<0时, f(x)=-x2-2x+3,对称轴为x=-1,抛物线开口向下,所以x∈[-∞,-1]时,f(x)为增函数;x∈[-1,0]时,f(x)为减函数;
