2.1.4函数的奇偶性

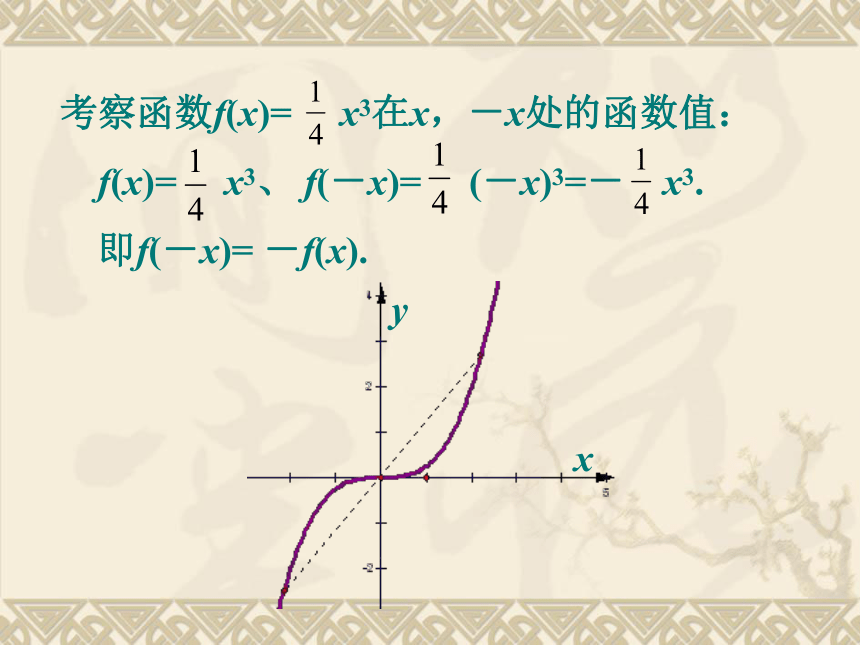
课件24张PPT。2.1.4 函数的奇偶性考察函数f(x)= x3在x，－x处的函数值：
f(x)= x3、 f(－x)= (－x)3=－ x3.
即f(－x)= －f(x).考察函数g(x)=x2在x，－x处的函数值：
g(x)=x2、 g(－x)=(－x)2=x2.
即g(－x)=g(x).1.函数奇偶性的概念:偶函数定义:
设函数y=f(x)定义域为D，如果对于D内的任意一个x, 都有－x∈D，且f(－x)=f(x),那么函数f(x)就叫偶函数.奇函数定义:
设函数y=f(x)定义域为D，如果对于D内的任意一个x, 都有－x∈D，且f(－x)= －f(x),那么函数f(x)就叫奇函数.对奇函数、偶函数定义的说明:（1）定义域关于原点对称是函数具有奇偶性的必要条件。 （2）奇、偶函数定义的逆命题也成立，即：
若f(x)为奇函数, 则f(－x)=－f(x)成立。
若f(x)为偶函数, 则f(－x)=f(x) 成立。（3） 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性。2.奇偶函数图象的性质: ⑴ 如果一个函数是奇函数，则这个函数的图象是以坐标原点为对称中心的中心对称图形.
反之，如果一个函数的图象是以坐标原点为对称中心的中心对称图形，则这个函数是奇函数. (2) 如果一个函数是偶函数，则它的图象是以y 轴为对称轴的对称图形.
反之，如果一个函数的图象是以y 轴为对称轴的对称图形，则这个函数是偶函数.练习1. 说出下列函数的奇偶性:偶函数奇函数奇函数奇函数①f(x)=x4 ________ ④ f(x)=x－1 _______ ② f(x)=x ________奇函数⑤f(x)=x－2 __________偶函数③ f(x)=x5 __________⑥f(x)=x－3 _______________ 说明：对于形如 f(x)=x n 的函数，
若n为偶数，则它为偶函数。
若n为奇数，则它为奇函数。说明：根据奇偶性, 函数可划分为四类:
奇函数；
偶函数；
既奇又偶函数；
非奇非偶函数.例1. 判断下列函数的奇偶性(1) f(x)=x3+2x； (2) g(x)=2x4+3x2。解: (1) f(－x)=(－x)3+2(－x)= －(x3+2x)= －f(x).
∴ f(x)=x3+2x是奇函数； (2) g(－x)=2(－x)4+3(－x)2= 2x4+3x2=g(x)，
∴ g(x)=2x4+3x2是偶函数。用定义判断函数奇偶性的步骤：(1) 先求定义域，看是否关于原点对称；(2)再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.(3)根据定义，作出结论 而函数的奇偶性是函数的整体性质；函数的单调性是函数的局部性质.例3.若函数f(x)=(m－1)x2+2mx+3是偶函数,求m的值.解：f(－x)=(m－1)(－x)2+2m(－x)+3
=(m－1)x2－2mx+3.
f(x)=(m－1)x2+2mx+3.
又函数f(x)是偶函数，f(－x)=f(x)，
∴ m=0.例4.判断函数 的奇偶性。解：原函数的定义域是使
成立的x的取值范围，即{x|－1≤x<0或0定义域关于原点对称.此时函数整理变形为 ，
f(－x)=－f(x)，∴ f(x)是奇函数例5. 判断下列函数是否具有奇偶性：
(1) f(x)=x+x3+x5； (2) f(x)=x2+1；
(3) f(x)=x+1；(4) f(x)=x2, x∈[－1, 3]解: (1) 是奇函数；
(2) 是偶函数；
(3) 是非奇非偶函数；
(4) 因为定义域关于原点不对称，所以f(x)既不是奇函数，也不是偶函数。例6. 研究函数 的性质并做出它的图象.解：已知函数的定义域是{x∈R| x≠0}，由函数的解析式可以推知，对任意的x的值，对应的函数值y>0，函数的图象在x轴的上方；
函数的图象在x=0处断开，函数的图象被分为两部分，且f(－x)=f(x)，这个函数为偶函数；
当x的绝对值变小时，函数值增大得非常快，当x的绝对值变大时，函数的图象向x轴的两个方向上靠近x轴.由以上分析，以x=0为中心，在x轴的两个方向上对称地选取若干个自变量的值，计算出对应的y值，列表如下：练习题:1.已知y=f(x)是偶函数，且在(－∞，0）上是增函数，则y=f(x)在(0,＋∞)上是（ ）
A. 增函数 B. 减函数
C. 非单调函数 D. 单调性不确定B2.已知偶函数y=f(x)在（0，4）上是增函数，
试比较f(－2), f(－3), f(1)的大小。解：由题意y=f(x)是偶函数，所以f(－2)=f(2), f(－3)=f(3), 又函数y=f(x)在(0，4)上是增函数，
所以f(1) (1) F(x)=f(x)+f(－x)； (2) G(x)=f(x) －f(－x)。解: (1) F(－x)=f(－x)+f(x)=F(x)，
所以F(x)是偶函数； (2) G(－x)=f(－x) －f(x)=－G(x)，
所以G(x)是奇函数；[－2,0)∪[2,+∞)5. 已知奇函数 y =f (x) 在其定义域上是增函数,那么 y =f (－x) 在它的定义域上 ( )A . 既是奇函数,又是增函数.
B . 既是奇函数,又是减函数.
C . 既是偶函数,又是先减后增函数.
D . 既是偶函数,又是先增后减函数. B 6. 定义在区间(－1，1)上的奇函数f(x)是其定义域上的减函数，并且满足f(1－m)+f(3－2m)<0，求m的取值范围.解：由定义域知m满足 ，即
，得1即f(1－m)2m－3，得m>∴