7.1.1 两条直线相交 课件(共20张PPT)
文档属性
| 名称 | 7.1.1 两条直线相交 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 14:00:41 | ||
图片预览







文档简介
(共20张PPT)
第七章 相交线与平行线
你对两条直线相交、平行一定不陌生吧!菜园篱笆上交叉的竹竿,笔直的公路上的车行道线,大桥的吊索、钢梁上的钢条,棋盘中的横线和竖线,教室里课桌面、黑板面相邻的两条边与相对的两条边……都给我们以相交线或平行线的形象.你能再举出一些相交线和平行线的实例吗?
本章我们将学习平面内不重合的两条直线的位置关系:相交与平行.
7.1 相交线
7.1.1 两条直线相交
1.理解邻补角与对顶角的概念.
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.(重难点)
情 境 导 入
观察下列图片,你能从中找出2条直线吗?
如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型.在转动木条的过程中,它们所成的角也在变化,你能发现这些角之间不变的关系吗?
探究1 任意画两条相交的直线,形成四个角(如图),∠1和∠2有怎样的位置关系?
∠1和∠2有一条公共边 OC;
∠1和∠2的另一边互为反向延长线.
具有这种位置关系的两个角,互为邻补角.
还有其他
邻补角吗?
A
B
C
D
2
3
1
4
O
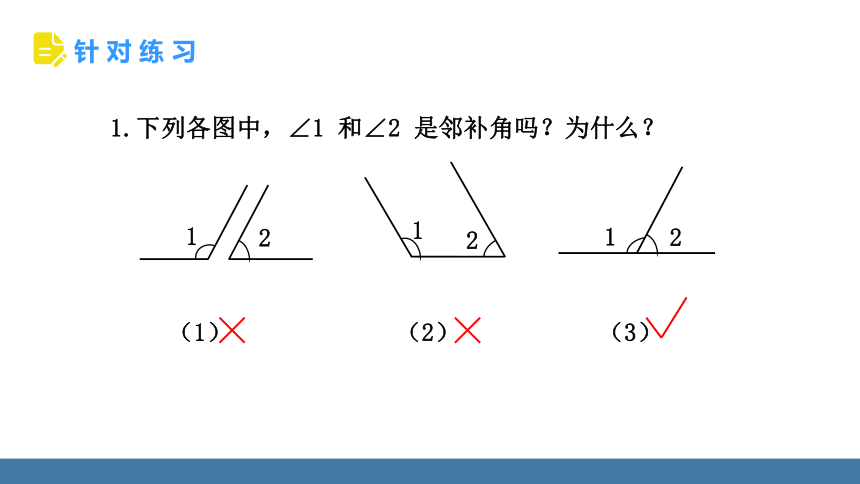
1.下列各图中,∠1 和∠2 是邻补角吗?为什么?
(1) (2) (3)
1
2
1
1
2
2
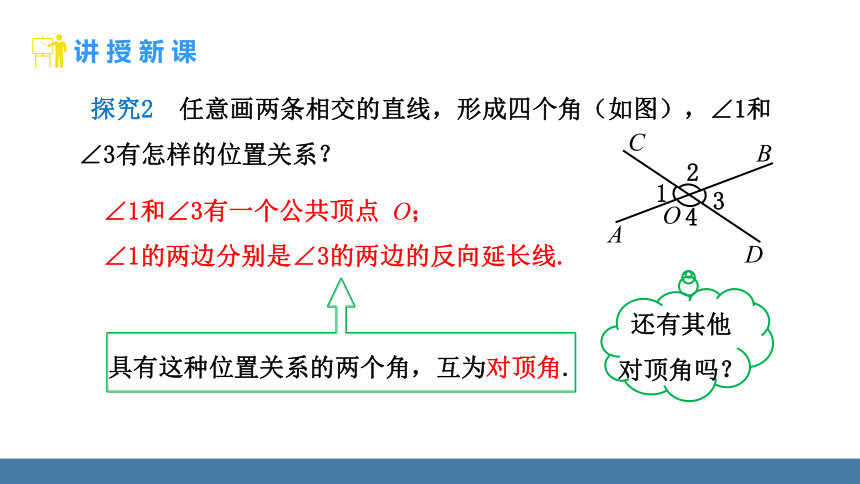
探究2 任意画两条相交的直线,形成四个角(如图),∠1和∠3有怎样的位置关系?
∠1和∠3有一个公共顶点 O;
∠1的两边分别是∠3的两边的反向延长线.
具有这种位置关系的两个角,互为对顶角.
还有其他
对顶角吗?
A
B
C
D
2
3
1
4
O
2.下列各图中,∠1 和 ∠2 是对顶角吗?为什么?
1
2
(2)
(3)
(4)
2
1
(1)
1
2
(5)
1
2
1
2
探究3 分别量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
∠1+∠2=180°;∠1=∠3.
改变两条直线相
交所成的角的大小,上述关系还保持吗?为什么?
可以得到∠3+∠2=180°.
归纳 补角的性质:同角的补角相等;
对顶角的性质:对顶角相等.
A
B
C
D
2
3
1
4
O
B
A
C
D
O
1
2
3
4
1.有公共顶点
归类
∠1和∠2
∠2和∠3 ∠3和∠4 ∠4和∠1
∠1和∠3
∠2和∠4
1.有公共顶点
位置关系
邻补角
对顶角
2.有一条公共边
3.另一边互为反向延长线
2.没有公共边
3.两边互为反向延长线
名称
数量关系
相等
互补
问题 你能利用有关知识来验证∠1 与∠3的数量关系吗?
因为∠1+∠2=180°,
∠3+∠2=180°,
所以∠1=∠3(同角的补角相等)
C
B
D
A
2
3
1
4
O
例1 如图,直线 a,b 相交,∠1=40°,求∠2,∠3,∠4的度数.
解:由∠1和∠2互为邻补角,得
∠2=180°-∠1
=180°-40°
=40°.
∠3=∠1=40°,∠4=∠2=140°.
由对顶角相等,得
a
b
2
1
3
4
例2 如图,直线 AB,CD 相交于点 O,OA 平分 ∠EOC,
∠EOC:∠EOD=1:2,求 ∠BOD 的度数.
解:∵∠EOC:∠EOD=1:2,
∠EOC+∠EOD =180°,
∴∠EOC=×180°=60°;
∵OA平分∠EOC,
∴∠AOC=∠EOC=30°,
∠BOD=∠AOC=30°.
A
E
C
D
B
O
1.如图,小明测出∠COD=110°,则两堵围墙所形成的∠AOB的度数为( )
A.70° B.90°
C.110° D.250°
2.如图,点 O 在直线上,若∠AOC=30°,则 ∠BOC 的度数是( )
A.30° B.60°
C.150° D.160°
C
C
3.如图,直线a,b相交,∠1=40°,则∠2-∠3等于( )
A.40° B.80° C.100° D.120°
4.如图所示,如果∠1+∠2=260°,则∠3的度数为 .
C
50°
第3题
第4题
5.如图:已知直线 AB、CD 相交于点 O,∠COE=90°,
(1)若∠AOC=36°,求 ∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数.
E
B
D
O
C
A
(1)解:∵∠COE=90°,∠AOC=36°
∴∠BOE=180°-∠AOC-∠COE
=180°-36°-90°
=54°;
5.如图:已知直线 AB、CD 相交于点 O,∠COE=90°,
(2)若∠BOD:∠BOC=1:5,求 ∠AOE 的度数.
E
B
D
O
C
A
(2)解:∵∠BOD:∠BOC=1:5,
∠BOD+∠BOC=180°,
∴∠BOD=30°,
∵∠BOD=∠AOC,
∴∠AOC=30°,
∴∠AOE=∠COE+∠AOC=90°+30°=120°.
对顶角
两条直线相交
①两条直线相交形成的角;
②有公共顶点;
③没有公共边
邻补角
①两条直线相交而成;
②有公共顶点;
③有一条公共边
对顶角相等
邻补角互补
第七章 相交线与平行线
你对两条直线相交、平行一定不陌生吧!菜园篱笆上交叉的竹竿,笔直的公路上的车行道线,大桥的吊索、钢梁上的钢条,棋盘中的横线和竖线,教室里课桌面、黑板面相邻的两条边与相对的两条边……都给我们以相交线或平行线的形象.你能再举出一些相交线和平行线的实例吗?
本章我们将学习平面内不重合的两条直线的位置关系:相交与平行.
7.1 相交线
7.1.1 两条直线相交
1.理解邻补角与对顶角的概念.
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.(重难点)
情 境 导 入
观察下列图片,你能从中找出2条直线吗?
如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型.在转动木条的过程中,它们所成的角也在变化,你能发现这些角之间不变的关系吗?
探究1 任意画两条相交的直线,形成四个角(如图),∠1和∠2有怎样的位置关系?
∠1和∠2有一条公共边 OC;
∠1和∠2的另一边互为反向延长线.
具有这种位置关系的两个角,互为邻补角.
还有其他
邻补角吗?
A
B
C
D
2
3
1
4
O
1.下列各图中,∠1 和∠2 是邻补角吗?为什么?
(1) (2) (3)
1
2
1
1
2
2
探究2 任意画两条相交的直线,形成四个角(如图),∠1和∠3有怎样的位置关系?
∠1和∠3有一个公共顶点 O;
∠1的两边分别是∠3的两边的反向延长线.
具有这种位置关系的两个角,互为对顶角.
还有其他
对顶角吗?
A
B
C
D
2
3
1
4
O
2.下列各图中,∠1 和 ∠2 是对顶角吗?为什么?
1
2
(2)
(3)
(4)
2
1
(1)
1
2
(5)
1
2
1
2
探究3 分别量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
∠1+∠2=180°;∠1=∠3.
改变两条直线相
交所成的角的大小,上述关系还保持吗?为什么?
可以得到∠3+∠2=180°.
归纳 补角的性质:同角的补角相等;
对顶角的性质:对顶角相等.
A
B
C
D
2
3
1
4
O
B
A
C
D
O
1
2
3
4
1.有公共顶点
归类
∠1和∠2
∠2和∠3 ∠3和∠4 ∠4和∠1
∠1和∠3
∠2和∠4
1.有公共顶点
位置关系
邻补角
对顶角
2.有一条公共边
3.另一边互为反向延长线
2.没有公共边
3.两边互为反向延长线
名称
数量关系
相等
互补
问题 你能利用有关知识来验证∠1 与∠3的数量关系吗?
因为∠1+∠2=180°,
∠3+∠2=180°,
所以∠1=∠3(同角的补角相等)
C
B
D
A
2
3
1
4
O
例1 如图,直线 a,b 相交,∠1=40°,求∠2,∠3,∠4的度数.
解:由∠1和∠2互为邻补角,得
∠2=180°-∠1
=180°-40°
=40°.
∠3=∠1=40°,∠4=∠2=140°.
由对顶角相等,得
a
b
2
1
3
4
例2 如图,直线 AB,CD 相交于点 O,OA 平分 ∠EOC,
∠EOC:∠EOD=1:2,求 ∠BOD 的度数.
解:∵∠EOC:∠EOD=1:2,
∠EOC+∠EOD =180°,
∴∠EOC=×180°=60°;
∵OA平分∠EOC,
∴∠AOC=∠EOC=30°,
∠BOD=∠AOC=30°.
A
E
C
D
B
O
1.如图,小明测出∠COD=110°,则两堵围墙所形成的∠AOB的度数为( )
A.70° B.90°
C.110° D.250°
2.如图,点 O 在直线上,若∠AOC=30°,则 ∠BOC 的度数是( )
A.30° B.60°
C.150° D.160°
C
C
3.如图,直线a,b相交,∠1=40°,则∠2-∠3等于( )
A.40° B.80° C.100° D.120°
4.如图所示,如果∠1+∠2=260°,则∠3的度数为 .
C
50°
第3题
第4题
5.如图:已知直线 AB、CD 相交于点 O,∠COE=90°,
(1)若∠AOC=36°,求 ∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数.
E
B
D
O
C
A
(1)解:∵∠COE=90°,∠AOC=36°
∴∠BOE=180°-∠AOC-∠COE
=180°-36°-90°
=54°;
5.如图:已知直线 AB、CD 相交于点 O,∠COE=90°,
(2)若∠BOD:∠BOC=1:5,求 ∠AOE 的度数.
E
B
D
O
C
A
(2)解:∵∠BOD:∠BOC=1:5,
∠BOD+∠BOC=180°,
∴∠BOD=30°,
∵∠BOD=∠AOC,
∴∠AOC=30°,
∴∠AOE=∠COE+∠AOC=90°+30°=120°.
对顶角
两条直线相交
①两条直线相交形成的角;
②有公共顶点;
③没有公共边
邻补角
①两条直线相交而成;
②有公共顶点;
③有一条公共边
对顶角相等
邻补角互补
同课章节目录
