7.1.3 同位角、内错角、同旁内角 课件(共21张PPT)
文档属性
| 名称 | 7.1.3 同位角、内错角、同旁内角 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 13:58:35 | ||
图片预览



文档简介
(共21张PPT)
7.1 相交线
7.1.3 同位角、内错角、同旁内角
1.理解同位角、内错角、同旁内角的概念.
2.结合图形识别同位角、内错角、同旁内角.(重点)
3.从复杂图形分解为基本图形的过程中,体会化繁为简、化难为易的化归思想.(难点)
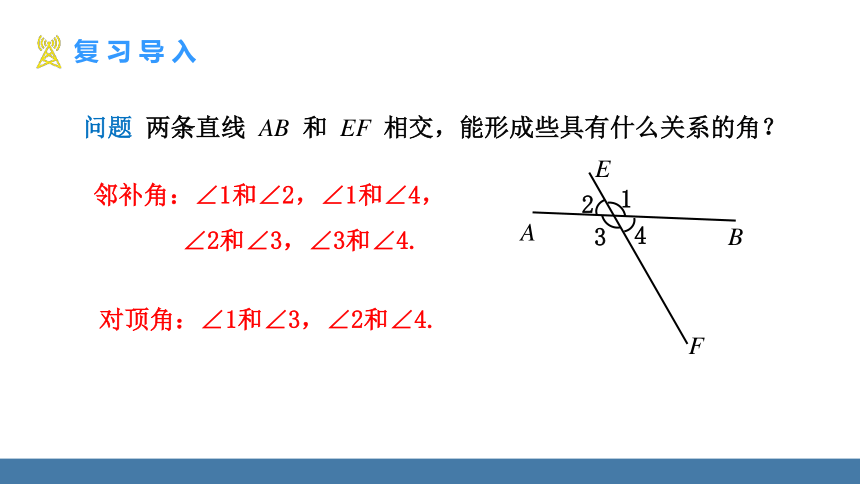
问题 两条直线 AB 和 EF 相交,能形成些具有什么关系的角?
邻补角:∠1和∠2,∠1和∠4,
∠2和∠3,∠3和∠4.
对顶角:∠1和∠3,∠2和∠4.
1
4
3
2
B
E
F
A
6
7
5
8
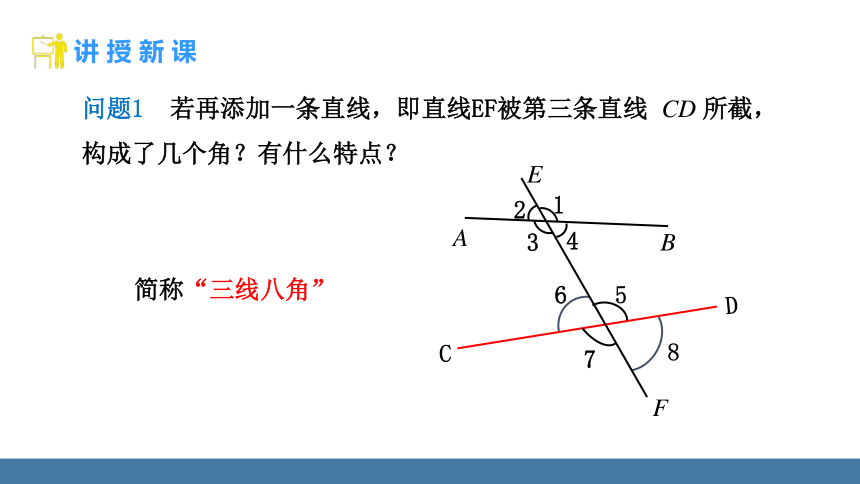
简称“三线八角”
问题1 若再添加一条直线,即直线EF被第三条直线 CD 所截,构成了几个角?有什么特点?
C
D
1
4
3
2
B
E
F
A
问题2 观察∠1和∠5的位置关系,有什么特点?
①都在直线EF的同侧(右侧)
②分别在直线 AB、CD 的同一侧(上方)
具有这种位置关系的一对角叫作同位角.
思考:∠2和∠6是同位角吗?图中还有其他同位角吗?
6
7
5
8
C
D
1
4
3
2
B
E
F
A
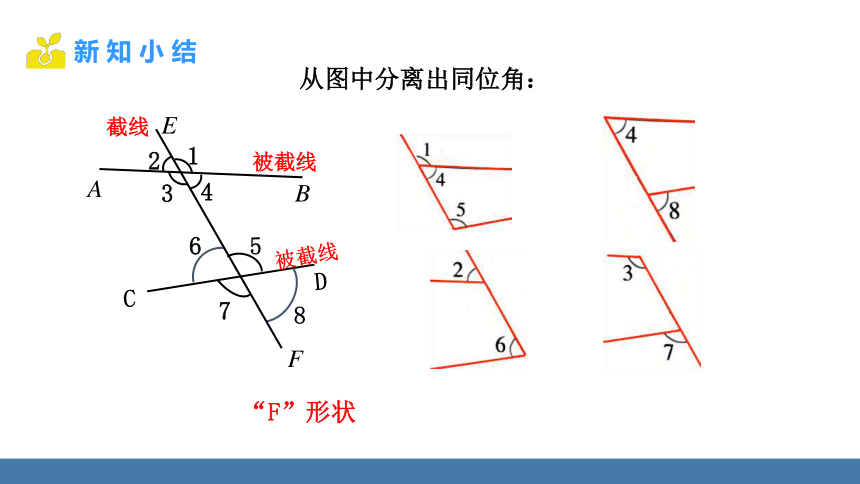
从图中分离出同位角:
“F”形状
6
7
5
8
C
D
1
4
3
2
B
E
F
A
截线
被截线
被截线
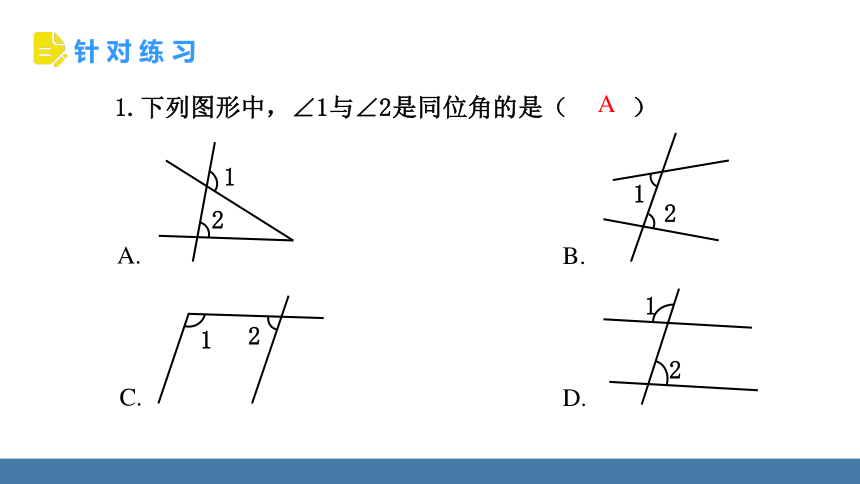
1.下列图形中,∠1与∠2是同位角的是( )
A
1
2
2
1
2
1
1
2
A.
B.
C.
D.
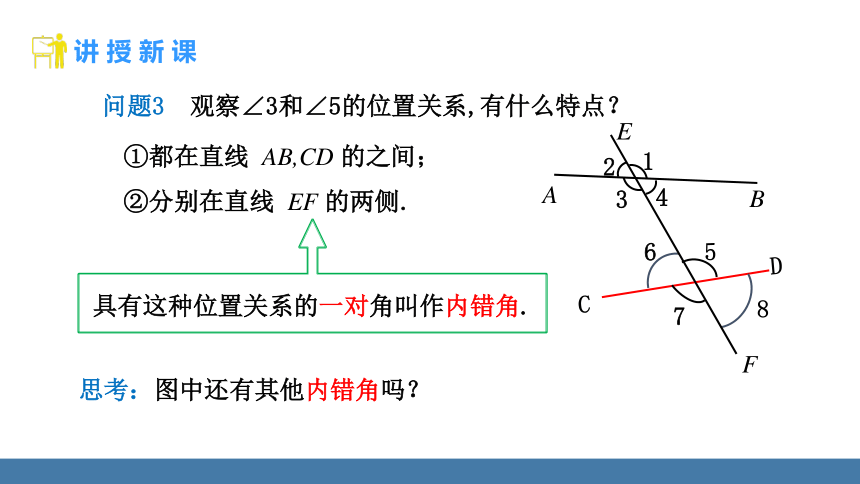
问题3 观察∠3和∠5的位置关系,有什么特点?
①都在直线 AB,CD 的之间;
②分别在直线 EF 的两侧.
具有这种位置关系的一对角叫作内错角.
思考:图中还有其他内错角吗?
6
7
5
8
C
D
1
4
3
2
B
E
F
A
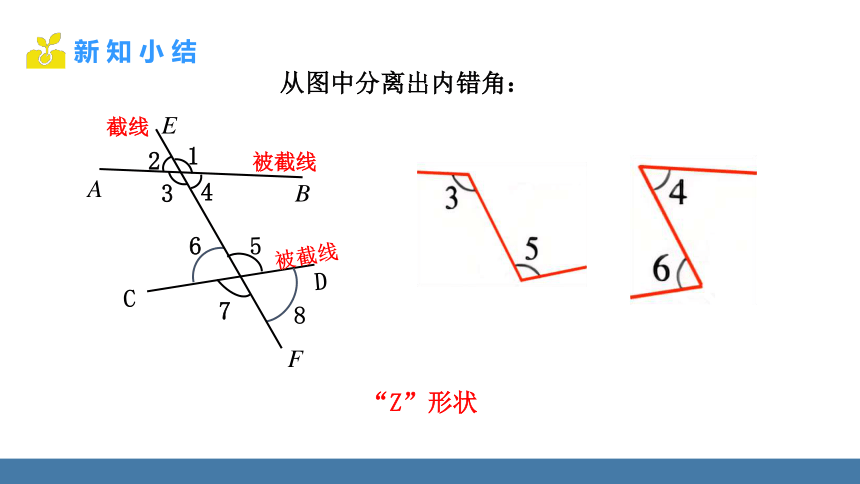
从图中分离出内错角:
“Z”形状
6
7
5
8
C
D
1
4
3
2
B
E
F
A
截线
被截线
被截线
2.下列四个图形中,∠1与∠2互为内错角的是( )
C
1
2
A.
B.
C.
D.
2
1
1
2
2
1
问题4 观察∠3和∠6的位置关系,有什么特点?
①都在直线 AB,CD 的之间;
②分别在直线EF的同一旁(左侧).
具有这种位置关系的一对角叫作同旁内角.
思考:图中还有其他同旁内角吗?
6
7
5
8
C
D
1
4
3
2
B
E
F
A
从图中分离出同旁内角:
“U”形状
6
7
5
8
C
D
1
4
3
2
B
E
F
A
截线
被截线
被截线
3.如图,在用数字标注的角中,∠4与 是同旁内角.
∠3与∠5
4
5
3
1
2
C
B
D
E
A
角的名称 角的特征 基本图形 基本图形 相同点 共同特征
同位角
同旁内角 内错角 F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的.
例 如图,直线 DE,BC 被直线AB所截.
(1)∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等
吗?∠1和∠3互补吗?为什么?
解:(1)∠1和∠2是内错角,
∠1和∠3是同旁内角,
∠1和∠4是同位角.
例 如图,直线 DE,BC 被直线AB所截.
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
解:(2)如果∠1=∠4.又由对顶角相等.
可得∠2=∠4因此∠1=∠2.
因为∠4和∠3互补,
所以∠4+∠3=180°.
又因为∠1=∠4,所以∠1+∠3=180°,
即∠1和∠3互补.
4
3
2
1
A
E
D
B
C
1.如图,∠DAB 和 ∠ABC 的位置关系是 ( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对
2.如图,∠1和∠2不能构成同位角的图形是( )
C
D
A
D
B
C
E
1
2
A
B
1
2
C
1
2
D
1
2
(1)如图1,若 ED,BF 被 AB 所截,则∠1与____是同位角.
3.看图填空:
∠2
(2)如图2,若 ED,BC 被 AF 所截,则∠3与___ 是内错角.
∠4
图1
图2
(3)如图3,∠1与∠3是 AB 和 AF 被_____所截构成的 角;
DE
内错
(4)如图4,∠2与∠4是 和 被 BC 所截构成的_ ___角.
AB
AF
同位
图3
图4
4.根据地图填空:
学校与游乐场所在的角形成一对( )角;
学校与超市所在的角形成一对( )角;
学校与飞机场所在的角形成一对( )角.
同位
同旁内
内错
同位角
三线八角
“F”型
“Z”型
内错角
同旁内角
“U”型
7.1 相交线
7.1.3 同位角、内错角、同旁内角
1.理解同位角、内错角、同旁内角的概念.
2.结合图形识别同位角、内错角、同旁内角.(重点)
3.从复杂图形分解为基本图形的过程中,体会化繁为简、化难为易的化归思想.(难点)
问题 两条直线 AB 和 EF 相交,能形成些具有什么关系的角?
邻补角:∠1和∠2,∠1和∠4,
∠2和∠3,∠3和∠4.
对顶角:∠1和∠3,∠2和∠4.
1
4
3
2
B
E
F
A
6
7
5
8
简称“三线八角”
问题1 若再添加一条直线,即直线EF被第三条直线 CD 所截,构成了几个角?有什么特点?
C
D
1
4
3
2
B
E
F
A
问题2 观察∠1和∠5的位置关系,有什么特点?
①都在直线EF的同侧(右侧)
②分别在直线 AB、CD 的同一侧(上方)
具有这种位置关系的一对角叫作同位角.
思考:∠2和∠6是同位角吗?图中还有其他同位角吗?
6
7
5
8
C
D
1
4
3
2
B
E
F
A
从图中分离出同位角:
“F”形状
6
7
5
8
C
D
1
4
3
2
B
E
F
A
截线
被截线
被截线
1.下列图形中,∠1与∠2是同位角的是( )
A
1
2
2
1
2
1
1
2
A.
B.
C.
D.
问题3 观察∠3和∠5的位置关系,有什么特点?
①都在直线 AB,CD 的之间;
②分别在直线 EF 的两侧.
具有这种位置关系的一对角叫作内错角.
思考:图中还有其他内错角吗?
6
7
5
8
C
D
1
4
3
2
B
E
F
A
从图中分离出内错角:
“Z”形状
6
7
5
8
C
D
1
4
3
2
B
E
F
A
截线
被截线
被截线
2.下列四个图形中,∠1与∠2互为内错角的是( )
C
1
2
A.
B.
C.
D.
2
1
1
2
2
1
问题4 观察∠3和∠6的位置关系,有什么特点?
①都在直线 AB,CD 的之间;
②分别在直线EF的同一旁(左侧).
具有这种位置关系的一对角叫作同旁内角.
思考:图中还有其他同旁内角吗?
6
7
5
8
C
D
1
4
3
2
B
E
F
A
从图中分离出同旁内角:
“U”形状
6
7
5
8
C
D
1
4
3
2
B
E
F
A
截线
被截线
被截线
3.如图,在用数字标注的角中,∠4与 是同旁内角.
∠3与∠5
4
5
3
1
2
C
B
D
E
A
角的名称 角的特征 基本图形 基本图形 相同点 共同特征
同位角
同旁内角 内错角 F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的.
例 如图,直线 DE,BC 被直线AB所截.
(1)∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等
吗?∠1和∠3互补吗?为什么?
解:(1)∠1和∠2是内错角,
∠1和∠3是同旁内角,
∠1和∠4是同位角.
例 如图,直线 DE,BC 被直线AB所截.
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
解:(2)如果∠1=∠4.又由对顶角相等.
可得∠2=∠4因此∠1=∠2.
因为∠4和∠3互补,
所以∠4+∠3=180°.
又因为∠1=∠4,所以∠1+∠3=180°,
即∠1和∠3互补.
4
3
2
1
A
E
D
B
C
1.如图,∠DAB 和 ∠ABC 的位置关系是 ( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对
2.如图,∠1和∠2不能构成同位角的图形是( )
C
D
A
D
B
C
E
1
2
A
B
1
2
C
1
2
D
1
2
(1)如图1,若 ED,BF 被 AB 所截,则∠1与____是同位角.
3.看图填空:
∠2
(2)如图2,若 ED,BC 被 AF 所截,则∠3与___ 是内错角.
∠4
图1
图2
(3)如图3,∠1与∠3是 AB 和 AF 被_____所截构成的 角;
DE
内错
(4)如图4,∠2与∠4是 和 被 BC 所截构成的_ ___角.
AB
AF
同位
图3
图4
4.根据地图填空:
学校与游乐场所在的角形成一对( )角;
学校与超市所在的角形成一对( )角;
学校与飞机场所在的角形成一对( )角.
同位
同旁内
内错
同位角
三线八角
“F”型
“Z”型
内错角
同旁内角
“U”型
同课章节目录
