8.1 平方根 第1课时 课件(共16张PPT)
文档属性
| 名称 | 8.1 平方根 第1课时 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 14:05:02 | ||
图片预览




文档简介
(共16张PPT)
8.1 平方根
第1课时 平方根
1.了解平方根的概念与性质,并理解平方与开平方的关系;
2.会求非负数的平方根.(重点、难点)
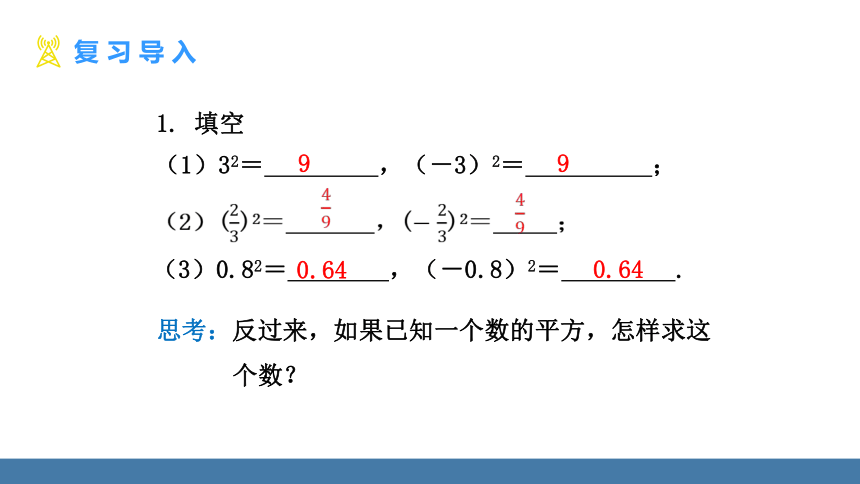
(1)32= ,(-3)2= ;
(2)()2= ,()2= ;
(3)0.82= ,(-0.8)2= .
9
0.64
0.64
1. 填空
9
思考:反过来,如果已知一个数的平方,怎样求这
个数?
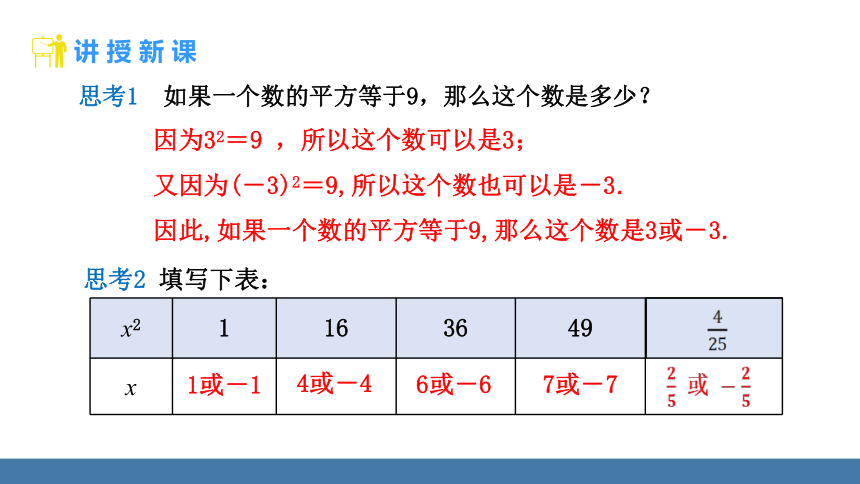
思考1 如果一个数的平方等于9,那么这个数是多少?
因为32=9 ,所以这个数可以是3;
又因为(-3)2=9,所以这个数也可以是-3.
因此,如果一个数的平方等于9,那么这个数是3或-3.
思考2 填写下表:
x2 1 16 36 49
x
1或-1
4或-4
6或-6
7或-7
或
一般地,如果一个数x的平方等于 a,即x2=a,那么这个数x叫做 a 的平方根或二次方根.
例如,3 和 -3 是 9 的平方根,
简记为 ±3 ,
则±3 是 9 的平方根.
平方根的定义:
-1
+1
+2
-2
+3
-3
1
4
9
平方
-1
+1
+2
-2
+3
-3
1
4
9
开平方
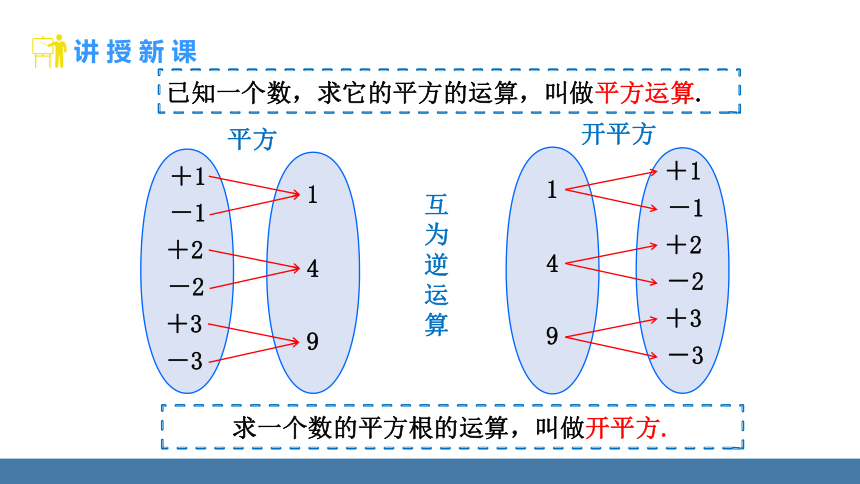
互为逆运算
已知一个数,求它的平方的运算,叫做平方运算.
求一个数的平方根的运算,叫做开平方.
例1 求下列各数的平方根:
(1) 64 ; (2) ; (3) 0.01.
解:(1) 因为 (±8)2 = 64,所以64 的平方根是 ±8;
(2) 因为 ,所以 的平方根是± ;
(3)因为 (±0.1)2 = 0.01,所以 0.01 的平方根是 ±0.1.
1.144的平方根是什么?它们有什么关系?
2.0的平方根是什么?
3.-4有没有平方根?为什么?
∵02 = 0,∴0的平方根是0.
没有,因为一个数的平方不可能是负数.
+12与-12互为相反数
试一试
±12
思考 正数的平方根有什么特点?0 的平方根是多少?负数有平方根吗?
正数的平方根有两个,它们互为相反数,
0的平方根是 0.
负数没有平方根.
平方根的性质:
正数 a 的正的平方根记为,读作“根号a”,a叫作被开方数;
正数 a 的负的平方根,可以用表示;
正数 a 的平方根可以用表示.读作“正、负根号 a ”.
特别地,0的平方根记为.
思考 只有当 a ≥ 0 时,有意义;而当a < 0 时,没有意义.为什么?
因为负数没有平方根.
例2 下列各数有平方根吗?如果有,求它的平方根:如果没有,说明理由.
(1)0.36; (2)-5; (3)(-4)2.
解:(1)因为0.36是正数,
所以0.36有两个平方根,±=±0.6;
(2)因为一5是负数,所以一5没有平方根;
(3)因为(-4) =16是正数,
所以(-4) 有两个平方根,±=±=±4.
例3 一个正数的两个平方根分别是 2a+1 和 a-4,求这个数.
解:由于一个正数的两个平方根是 2a+1 和 a-4,
则有 2a+1+a-4=0,即 3a-3=0,
解得 a=1.
所以这个数为 (2a+1)2=(2+1)2=9.
方法归纳:一个正数有两个平方根,它们互为相反数.
1.下列说法正确的是_________.
① -3是9的平方根; ②25的平方根是5;
③ -36的平方根是-6; ④平方根等于0的数是0;
⑤ 7的平方根是±.
①④⑤
2.a-1的平方根是±4,则a= .
17
3. 判断下列说法是否正确.
(1)是的一个平方根;
(2)0.1的平方根是±0.01;
(3)(-3)2的平方根是-3.
√
×
0.01的平方根是±0.1
×
∵(-3)2的值为9 ,
9的平方根是±3,
∴(-3)2的平方根是±3
4.分别求64,,6.25的平方根.
解:64的平方根是8与-8,
的平方根是 与 ,
6.25的平方根是2.5与-2.5.
5.求下列各式中 x 的值:
(1)3x -12=0; (2)(x-2) =25.
(1)解:3x -12=0,
移项得:3x =12,
两边同除以3得:x =4,
两边开方得:x=2或x=-2
(2)解:(x-2) =25
x-2=5或x-2=-5,
解得:x=7或x=-3
平方根的概念
平方根
平方根的性质
开平方及相关运算
8.1 平方根
第1课时 平方根
1.了解平方根的概念与性质,并理解平方与开平方的关系;
2.会求非负数的平方根.(重点、难点)
(1)32= ,(-3)2= ;
(2)()2= ,()2= ;
(3)0.82= ,(-0.8)2= .
9
0.64
0.64
1. 填空
9
思考:反过来,如果已知一个数的平方,怎样求这
个数?
思考1 如果一个数的平方等于9,那么这个数是多少?
因为32=9 ,所以这个数可以是3;
又因为(-3)2=9,所以这个数也可以是-3.
因此,如果一个数的平方等于9,那么这个数是3或-3.
思考2 填写下表:
x2 1 16 36 49
x
1或-1
4或-4
6或-6
7或-7
或
一般地,如果一个数x的平方等于 a,即x2=a,那么这个数x叫做 a 的平方根或二次方根.
例如,3 和 -3 是 9 的平方根,
简记为 ±3 ,
则±3 是 9 的平方根.
平方根的定义:
-1
+1
+2
-2
+3
-3
1
4
9
平方
-1
+1
+2
-2
+3
-3
1
4
9
开平方
互为逆运算
已知一个数,求它的平方的运算,叫做平方运算.
求一个数的平方根的运算,叫做开平方.
例1 求下列各数的平方根:
(1) 64 ; (2) ; (3) 0.01.
解:(1) 因为 (±8)2 = 64,所以64 的平方根是 ±8;
(2) 因为 ,所以 的平方根是± ;
(3)因为 (±0.1)2 = 0.01,所以 0.01 的平方根是 ±0.1.
1.144的平方根是什么?它们有什么关系?
2.0的平方根是什么?
3.-4有没有平方根?为什么?
∵02 = 0,∴0的平方根是0.
没有,因为一个数的平方不可能是负数.
+12与-12互为相反数
试一试
±12
思考 正数的平方根有什么特点?0 的平方根是多少?负数有平方根吗?
正数的平方根有两个,它们互为相反数,
0的平方根是 0.
负数没有平方根.
平方根的性质:
正数 a 的正的平方根记为,读作“根号a”,a叫作被开方数;
正数 a 的负的平方根,可以用表示;
正数 a 的平方根可以用表示.读作“正、负根号 a ”.
特别地,0的平方根记为.
思考 只有当 a ≥ 0 时,有意义;而当a < 0 时,没有意义.为什么?
因为负数没有平方根.
例2 下列各数有平方根吗?如果有,求它的平方根:如果没有,说明理由.
(1)0.36; (2)-5; (3)(-4)2.
解:(1)因为0.36是正数,
所以0.36有两个平方根,±=±0.6;
(2)因为一5是负数,所以一5没有平方根;
(3)因为(-4) =16是正数,
所以(-4) 有两个平方根,±=±=±4.
例3 一个正数的两个平方根分别是 2a+1 和 a-4,求这个数.
解:由于一个正数的两个平方根是 2a+1 和 a-4,
则有 2a+1+a-4=0,即 3a-3=0,
解得 a=1.
所以这个数为 (2a+1)2=(2+1)2=9.
方法归纳:一个正数有两个平方根,它们互为相反数.
1.下列说法正确的是_________.
① -3是9的平方根; ②25的平方根是5;
③ -36的平方根是-6; ④平方根等于0的数是0;
⑤ 7的平方根是±.
①④⑤
2.a-1的平方根是±4,则a= .
17
3. 判断下列说法是否正确.
(1)是的一个平方根;
(2)0.1的平方根是±0.01;
(3)(-3)2的平方根是-3.
√
×
0.01的平方根是±0.1
×
∵(-3)2的值为9 ,
9的平方根是±3,
∴(-3)2的平方根是±3
4.分别求64,,6.25的平方根.
解:64的平方根是8与-8,
的平方根是 与 ,
6.25的平方根是2.5与-2.5.
5.求下列各式中 x 的值:
(1)3x -12=0; (2)(x-2) =25.
(1)解:3x -12=0,
移项得:3x =12,
两边同除以3得:x =4,
两边开方得:x=2或x=-2
(2)解:(x-2) =25
x-2=5或x-2=-5,
解得:x=7或x=-3
平方根的概念
平方根
平方根的性质
开平方及相关运算
同课章节目录
