8.1 平方根 第2课时 算术平方根 课件(共20张PPT)
文档属性
| 名称 | 8.1 平方根 第2课时 算术平方根 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 14:04:32 | ||
图片预览








文档简介
(共20张PPT)
8.2 平方根
第2课时 算术平方根
1.了解算术平方根的概念,会用根号表示一个数的算术平方根.(重点)
2.会求非负数的算术平方根,掌握算术平方根的非负性.(重难点)
1. 正数的平方根有什么特点?
2. 0 的平方根是多少?
3. 负数有平方根吗?
正数的平方根有两个,它们互为相反数,
0 的平方根是 0.
负数没有平方根.
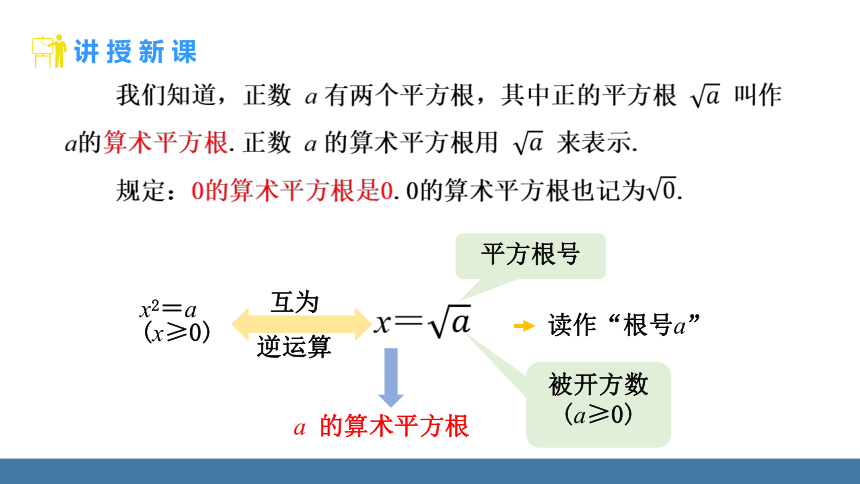
我们知道,正数 a 有两个平方根,其中正的平方根 叫作 a的算术平方根.正数 a 的算术平方根用 来表示.
规定:0的算术平方根是0.0的算术平方根也记为.
a 的算术平方根
互为
逆运算
平方根号
被开方数(a≥0)
读作“根号a”
x2=a
(x≥0)
x=
例1 分别求下列各数的算术平方根:
(1) 100; (2) ; (3) 0.0001.
解:(1) 由于102=100, 因此 10.
(2)由于 ,因此 .
(3) 由于 0.012=0.0001,因此 .
被开方数越大,对应的算术平方根也越大.
思考1 被开方数 a 可以是负数吗?
思考2 算术平方根可以是负数吗?
答:不可以,由算术平方根的定义可得正数x=,即>0,又=0, 所以也是一个非负数.
答:不可以,因为任意一个数的平方都不可能是负数. 即 a 是一个非负数.
a 的算术平方根
非负数
非负数
算术平方根的双重非负性:
到目前为止,表示非负数的式子有:
|a|≥0;a2≥0;当a≥0 时,≥0.
解: 因为 |a-5| ≥0, ≥0,
且 |a-5|+ =0,
所以 |a-5|=0, =0,
所以 a=5,b=-1,
所以 a+b=5+(-1)=4.
例2 若 |a-5|+ =0,求 m+n 的值.
归纳 若几个非负数的和为0,则每个数均为0.
例3 求下列各式的值:
(1) ;(2) ; (3)± ;
解:(1) =6 ;
(2) = -0.9 ;
(3)± = ± .
平方根与算术平方根的联系与区别
联系
区别
1. 包含关系:平方根包含算术平方根,算术平方根是平方根的一种.
2. 只有非负数才有平方根和算术平方根.
3. 0 的平方根是 0,算术平方根也是 0.
1. 个数不同:一个正数有两个平方根,但只有一个算术平方根.
2. 表示法不同:平方根表示为± ,而算术平方根表示为.
探究1 怎样用两个面积为1 dm2的小正方形拼成一个面积为2 dm 的大正方形?
如图,把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2 dm2的大正方形.
设大正方形的边长为 x dm,则
x =2.
由边长的实际意义可知x=,
所以大正方形的边长是 dm.
拼成的这个面积为 2 dm2 的大正方形的边长应该是多少呢?
探究2 有多大呢?
∵12=1,22=4,12<2<22,∴1<<2;
是整数部分是1 的小数
∵1.42=1.96,1.52=2.25,1.42<2<1.52,
∴1.4<<1.5;
∵1.412=1.988 1,1.422=2.016 4,1.412<2<1.422,
∴1.41<<1.42;
∵1.4142=1.999 396,1.4152=2.002 225,1.4142<2<1.4152,
∴1.414<<1.415;
……
事实上,=1.414 213 562 373…,它是一个无限不循环小数.
实际上,很多正有理数的算术平方根(例如,,等)都是无限不循环小数.
无限不循环小数是指小数位数无限,且小数部分不循环的小数.
1.3的算术平方根为( )
A. B.-3 C.±3 D.±
2.面积为9的正方形,其边长等于( )
A.9的平方根 B.3的算术平方根
C.9的算术平方根 D.3的平方根
3.若|a-17|+(b-1) =0,则的算术平方根为____.
A
C
2
4.求下列各式的值:
(1) ; (2) ; (3)± .
解:(1)=12 ;
(2) = -0.9 ;
(3)± = ± .
5.已知:m、n满足+n +9=6n,求(m+n)100的值.
解:∵+n +9=6n,
∴+n +9-6n=0,
∴+(n-3) =0,
∴m+2=0,n-3=0,
∴m=-2,n=3,
∴(m+n)100=(-2+3)100=1.
6.如图,有一张长宽比为3:2的长方形纸片 ABCD,面积为 96 cm .
(1)分别求长方形纸片的长和宽;
(2)小丽想沿这张长方形纸片边的方
向裁剪一块长宽比为 6:5 的新长方形,
使其面积为 90 cm ,请问她能裁出符合
要求的长方形吗 试说明理由.
A
B
C
D
(1)解:设长方形的长为 3x cm,宽为 2x cm,根据题意得:3x·2x=96,解得:x=4(负值舍去),
∴3x=12,2x=8.
答:长方形纸片的长和宽分别是 12 cm,8 cm;
(2)解:不能,理由如下:
设长方形纸片的长为 6a cm,则宽为 5a cm,
根据题意得:6a·5a=90,
解得:a=(负值舍去),
∴6a=6<12,5a=5>8,
∴她不能裁出符合要求的长方形.
定义
算术平方根
性质
应用
8.2 平方根
第2课时 算术平方根
1.了解算术平方根的概念,会用根号表示一个数的算术平方根.(重点)
2.会求非负数的算术平方根,掌握算术平方根的非负性.(重难点)
1. 正数的平方根有什么特点?
2. 0 的平方根是多少?
3. 负数有平方根吗?
正数的平方根有两个,它们互为相反数,
0 的平方根是 0.
负数没有平方根.
我们知道,正数 a 有两个平方根,其中正的平方根 叫作 a的算术平方根.正数 a 的算术平方根用 来表示.
规定:0的算术平方根是0.0的算术平方根也记为.
a 的算术平方根
互为
逆运算
平方根号
被开方数(a≥0)
读作“根号a”
x2=a
(x≥0)
x=
例1 分别求下列各数的算术平方根:
(1) 100; (2) ; (3) 0.0001.
解:(1) 由于102=100, 因此 10.
(2)由于 ,因此 .
(3) 由于 0.012=0.0001,因此 .
被开方数越大,对应的算术平方根也越大.
思考1 被开方数 a 可以是负数吗?
思考2 算术平方根可以是负数吗?
答:不可以,由算术平方根的定义可得正数x=,即>0,又=0, 所以也是一个非负数.
答:不可以,因为任意一个数的平方都不可能是负数. 即 a 是一个非负数.
a 的算术平方根
非负数
非负数
算术平方根的双重非负性:
到目前为止,表示非负数的式子有:
|a|≥0;a2≥0;当a≥0 时,≥0.
解: 因为 |a-5| ≥0, ≥0,
且 |a-5|+ =0,
所以 |a-5|=0, =0,
所以 a=5,b=-1,
所以 a+b=5+(-1)=4.
例2 若 |a-5|+ =0,求 m+n 的值.
归纳 若几个非负数的和为0,则每个数均为0.
例3 求下列各式的值:
(1) ;(2) ; (3)± ;
解:(1) =6 ;
(2) = -0.9 ;
(3)± = ± .
平方根与算术平方根的联系与区别
联系
区别
1. 包含关系:平方根包含算术平方根,算术平方根是平方根的一种.
2. 只有非负数才有平方根和算术平方根.
3. 0 的平方根是 0,算术平方根也是 0.
1. 个数不同:一个正数有两个平方根,但只有一个算术平方根.
2. 表示法不同:平方根表示为± ,而算术平方根表示为.
探究1 怎样用两个面积为1 dm2的小正方形拼成一个面积为2 dm 的大正方形?
如图,把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2 dm2的大正方形.
设大正方形的边长为 x dm,则
x =2.
由边长的实际意义可知x=,
所以大正方形的边长是 dm.
拼成的这个面积为 2 dm2 的大正方形的边长应该是多少呢?
探究2 有多大呢?
∵12=1,22=4,12<2<22,∴1<<2;
是整数部分是1 的小数
∵1.42=1.96,1.52=2.25,1.42<2<1.52,
∴1.4<<1.5;
∵1.412=1.988 1,1.422=2.016 4,1.412<2<1.422,
∴1.41<<1.42;
∵1.4142=1.999 396,1.4152=2.002 225,1.4142<2<1.4152,
∴1.414<<1.415;
……
事实上,=1.414 213 562 373…,它是一个无限不循环小数.
实际上,很多正有理数的算术平方根(例如,,等)都是无限不循环小数.
无限不循环小数是指小数位数无限,且小数部分不循环的小数.
1.3的算术平方根为( )
A. B.-3 C.±3 D.±
2.面积为9的正方形,其边长等于( )
A.9的平方根 B.3的算术平方根
C.9的算术平方根 D.3的平方根
3.若|a-17|+(b-1) =0,则的算术平方根为____.
A
C
2
4.求下列各式的值:
(1) ; (2) ; (3)± .
解:(1)=12 ;
(2) = -0.9 ;
(3)± = ± .
5.已知:m、n满足+n +9=6n,求(m+n)100的值.
解:∵+n +9=6n,
∴+n +9-6n=0,
∴+(n-3) =0,
∴m+2=0,n-3=0,
∴m=-2,n=3,
∴(m+n)100=(-2+3)100=1.
6.如图,有一张长宽比为3:2的长方形纸片 ABCD,面积为 96 cm .
(1)分别求长方形纸片的长和宽;
(2)小丽想沿这张长方形纸片边的方
向裁剪一块长宽比为 6:5 的新长方形,
使其面积为 90 cm ,请问她能裁出符合
要求的长方形吗 试说明理由.
A
B
C
D
(1)解:设长方形的长为 3x cm,宽为 2x cm,根据题意得:3x·2x=96,解得:x=4(负值舍去),
∴3x=12,2x=8.
答:长方形纸片的长和宽分别是 12 cm,8 cm;
(2)解:不能,理由如下:
设长方形纸片的长为 6a cm,则宽为 5a cm,
根据题意得:6a·5a=90,
解得:a=(负值舍去),
∴6a=6<12,5a=5>8,
∴她不能裁出符合要求的长方形.
定义
算术平方根
性质
应用
同课章节目录
