8.2 立方根 第2课时 立方根(2) 课件(共18张PPT)
文档属性
| 名称 | 8.2 立方根 第2课时 立方根(2) 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 14:15:23 | ||
图片预览





文档简介
(共18张PPT)
8.2 立方根
第2课时 立方根(2)
1.能运用开立方与立方之间互为逆运算的关系求一个数的立方根.
2.能用计算器求立方根或立方根的近似值,知道立方根的小数点的位置移动规律.(重难点)
因为 = , = ;
因为 = , = .
-2
-2
-3
-3
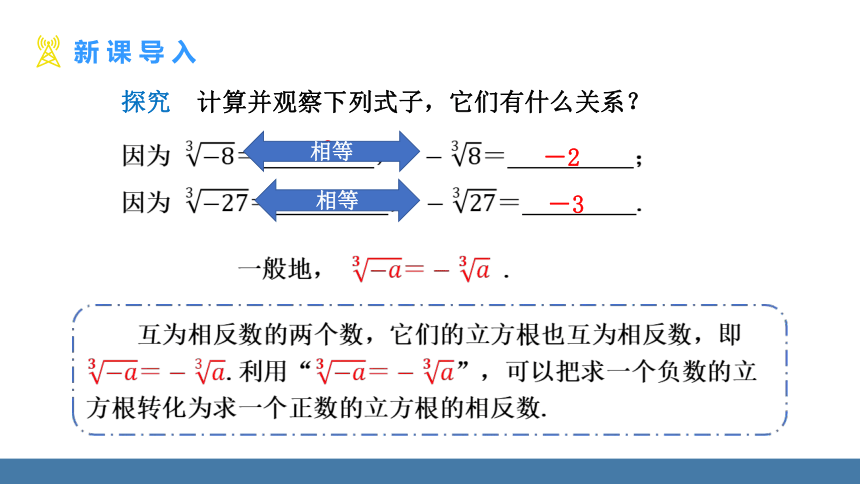
探究 计算并观察下列式子,它们有什么关系?
一般地, .
互为相反数的两个数,它们的立方根也互为相反数,即.利用“”,可以把求一个负数的立方根转化为求一个正数的立方根的相反数.
相等
相等
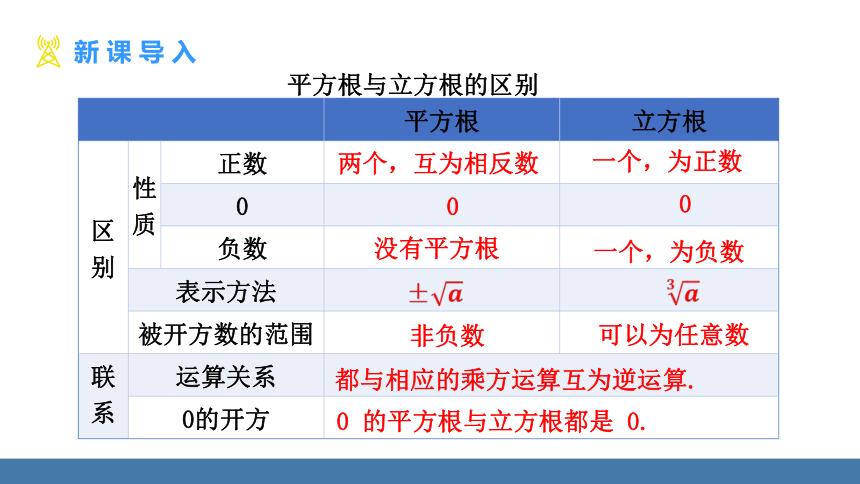
平方根 立方根
区别 性 质 正数
0
负数
表示方法
被开方数的范围
联系 运算关系 0的开方 两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
可以为任意数
非负数
±
都与相应的乘方运算互为逆运算.
0 的平方根与立方根都是 0.
平方根与立方根的区别
例1 求下列各式的值:
(1) ; (2) ; (3) .
解:(1) ;
(2) ;
(3) .
实际上,很多有理数的立方根(如 , ,)是无限不循环小数.我们可以用有理数近似地表示它们.
试一试(1)用计算器求.(2)用计算器求.
(1)依次按键 ,
显示:13
所以=13.
2
1
9
7
=
有些计算器需要调用备用功能求一个数的立方根,具体操作参见计算器的使用说明.
(2)依次按键 ,
显示近似值:1.442249570
所以≈1.442.
3
=
探究1 用计算器计算…, , , , ,…,你能发现什么规律?
=0.06,
=0.6 ,
=6,
=60,
归纳 被开方数的小数点向左或向右移动 3n 位时,立方根的小数点就相应地向左或向右移动 n 位( n 为正整数).
探究2 用计算器计算 (精确到0.001),并利用你发现的规律求 , , 的近似值.
=4.642,
=0.4 642 ,
=0.04 642,
=46.42.
例2 比较大小:(1)和-3 ;(2)与-3.4 .
解:(1)∵-3=,-26>-27,
∴>
即>-3.
(2)∵() =42,3.4 =39.304,42>39.304,
∴>3.4,
∴-<-3.4.
例3 求下列各式中 x 的值.
(1) x3-0.001=0;(2) 8x3+125=0;(3) (x+3)3+27=0.
解:(1)∵x3-0.001=0 ,
∴ x3=0.001,
∴ x==0.1.
(2) ∵ 8x3+125=0,
∴ 8x3=-125,
∴ x3= ,
∴ x= .
(3) ∵(x+3)3+27=0 ,
∴(x+3)3=-27,
∴ x+3= =-3,
∴ x=-6.
利用立方根的概念解方程的步骤
1.把原方程化为 x3=m 或 (ax+b)3=m 的形式.
2.利用立方根的概念,直接开立方求出 x 的值或将方程变为一元一次方程.
3.解所得的一元一次方程,求出 x 的值.
例4 已知一个正方体的体积为 125cm3.
(1)求正方体的棱长
(2)若将正方体的体积变为原来的 8 倍,则它的棱长变为原来的多少倍?
解:(1)设正方体的棱长为 xcm,
根据题意得,x =125,
解得 x=5,
答:正方体的棱长 5cm;
(2)设棱长变为原来的 y 倍,
根据题意得,(5y)3=125×8,
解得 y=2,
答:棱长变为原来的 2 倍.
1.利用计算器求+的值,其按键顺序正确的是( )
A
A.
B.
C.
D.
8
+
2ndF
6
=
8
+
2ndF
6
=
8
+
6
=
8
+
6
=
2. 已知=0.7,则=_____;
=______.
70
-0.07
3.求下列各式的值.
(1);(2);(3);(4).
=-0.3
=-
=
=
=
=-
4.求 x 的值:
(1)x +27=0; (2)2(x+1) +16=0.
(1)解:∵x +27=0,
∴x =-27,
∴x=-3.
(2)解:由2(x+1) +16=0,
得:(x+1) =-8,
开立方得:x+1=-2,
解得:x=-3.
5.比较3,4,的大小.
解:33= 27,43 = 64
因为27<50<64
所以3<<4
6.立方根概念的起源与几何中的正方体有关,如果一个正方体的体积为 V,那么这个正方体的棱长为多少?
解:
运算
配方法
开立方
用计算器求立方根
8.2 立方根
第2课时 立方根(2)
1.能运用开立方与立方之间互为逆运算的关系求一个数的立方根.
2.能用计算器求立方根或立方根的近似值,知道立方根的小数点的位置移动规律.(重难点)
因为 = , = ;
因为 = , = .
-2
-2
-3
-3
探究 计算并观察下列式子,它们有什么关系?
一般地, .
互为相反数的两个数,它们的立方根也互为相反数,即.利用“”,可以把求一个负数的立方根转化为求一个正数的立方根的相反数.
相等
相等
平方根 立方根
区别 性 质 正数
0
负数
表示方法
被开方数的范围
联系 运算关系 0的开方 两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
可以为任意数
非负数
±
都与相应的乘方运算互为逆运算.
0 的平方根与立方根都是 0.
平方根与立方根的区别
例1 求下列各式的值:
(1) ; (2) ; (3) .
解:(1) ;
(2) ;
(3) .
实际上,很多有理数的立方根(如 , ,)是无限不循环小数.我们可以用有理数近似地表示它们.
试一试(1)用计算器求.(2)用计算器求.
(1)依次按键 ,
显示:13
所以=13.
2
1
9
7
=
有些计算器需要调用备用功能求一个数的立方根,具体操作参见计算器的使用说明.
(2)依次按键 ,
显示近似值:1.442249570
所以≈1.442.
3
=
探究1 用计算器计算…, , , , ,…,你能发现什么规律?
=0.06,
=0.6 ,
=6,
=60,
归纳 被开方数的小数点向左或向右移动 3n 位时,立方根的小数点就相应地向左或向右移动 n 位( n 为正整数).
探究2 用计算器计算 (精确到0.001),并利用你发现的规律求 , , 的近似值.
=4.642,
=0.4 642 ,
=0.04 642,
=46.42.
例2 比较大小:(1)和-3 ;(2)与-3.4 .
解:(1)∵-3=,-26>-27,
∴>
即>-3.
(2)∵() =42,3.4 =39.304,42>39.304,
∴>3.4,
∴-<-3.4.
例3 求下列各式中 x 的值.
(1) x3-0.001=0;(2) 8x3+125=0;(3) (x+3)3+27=0.
解:(1)∵x3-0.001=0 ,
∴ x3=0.001,
∴ x==0.1.
(2) ∵ 8x3+125=0,
∴ 8x3=-125,
∴ x3= ,
∴ x= .
(3) ∵(x+3)3+27=0 ,
∴(x+3)3=-27,
∴ x+3= =-3,
∴ x=-6.
利用立方根的概念解方程的步骤
1.把原方程化为 x3=m 或 (ax+b)3=m 的形式.
2.利用立方根的概念,直接开立方求出 x 的值或将方程变为一元一次方程.
3.解所得的一元一次方程,求出 x 的值.
例4 已知一个正方体的体积为 125cm3.
(1)求正方体的棱长
(2)若将正方体的体积变为原来的 8 倍,则它的棱长变为原来的多少倍?
解:(1)设正方体的棱长为 xcm,
根据题意得,x =125,
解得 x=5,
答:正方体的棱长 5cm;
(2)设棱长变为原来的 y 倍,
根据题意得,(5y)3=125×8,
解得 y=2,
答:棱长变为原来的 2 倍.
1.利用计算器求+的值,其按键顺序正确的是( )
A
A.
B.
C.
D.
8
+
2ndF
6
=
8
+
2ndF
6
=
8
+
6
=
8
+
6
=
2. 已知=0.7,则=_____;
=______.
70
-0.07
3.求下列各式的值.
(1);(2);(3);(4).
=-0.3
=-
=
=
=
=-
4.求 x 的值:
(1)x +27=0; (2)2(x+1) +16=0.
(1)解:∵x +27=0,
∴x =-27,
∴x=-3.
(2)解:由2(x+1) +16=0,
得:(x+1) =-8,
开立方得:x+1=-2,
解得:x=-3.
5.比较3,4,的大小.
解:33= 27,43 = 64
因为27<50<64
所以3<<4
6.立方根概念的起源与几何中的正方体有关,如果一个正方体的体积为 V,那么这个正方体的棱长为多少?
解:
运算
配方法
开立方
用计算器求立方根
同课章节目录
