期末重难点真题检测卷-2024-2025学年数学九年级上册北师大版(含解析)
文档属性
| 名称 | 期末重难点真题检测卷-2024-2025学年数学九年级上册北师大版(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 706.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 14:20:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末重难点真题检测卷-2024-2025学年数学九年级上册北师大版
一.选择题(共10小题)
1.(2023秋 双辽市期末)已知2a=3b(ab≠0),则下列比例式成立的是( )
A.= B.= C.= D.=
2.(2023秋 静安区期末)下列选项中的两个图形一定相似的是( )
A.两个平行四边形 B.两个圆
C.两个菱形 D.两个等腰三角形
3.(2023秋 宁都县期末)已知△ABC∽△DEF,且周长之比为2:3,则面积比为( )
A.2:3 B.4:9 C.9:4 D.16:81
4.(2023秋 贵阳期末)2023年12月16日,贵阳市轨道交通三号线正式运营.某校共有1000个学生,随机调查了100个学生,其中有16个学生在三号线开通首日乘坐了地铁三号线.在该校随机问一个学生,他在三号线开通首日乘坐该地铁的概率大约是( )
A.0.016 B.0.1 C.0.116 D.0.16
5.(2022秋 锦江区期末)如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B的坐标是(6,2),点D的坐标是(0,2),点A在x轴上,则点C的坐标是( )
A.(3,2) B.(3,3) C.(3,4) D.(2,4)
6.(2023秋 确山县期末)若x=2是关于x的一元二次方程x2+mx﹣2=0的一个根,则m的值为( )
A.1 B.3 C.﹣1 D.﹣3
7.(2023秋 太康县期末)在如图所示的电路中,随机闭合开关S1、S2、S3中的两个,能让灯泡L1发光的概率是( )
A. B. C. D.
8.(2023秋 息县期末)近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,某款燃油汽车2月份的售价为23万元,4月份售价为18.63万元,设该款汽车这两月售价的月平均降价率是x,可列方程正确的是( )
A.18.63(1+x)2=23 B.23(1﹣x)2=18.63
C.18.63(1﹣x)2=23 D.23(1﹣2x)=18.63
9.(2023春 槐荫区期末)如图,点A是反比例函数在第二象限内图象上一点,点B是反比例函数在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,则△AOB的面积是( )
A.2 B.2.5 C.3 D.3.5
10.(2023秋 城阳区期末)如图,在平面直角坐标系中,大鱼与小鱼是关于原点O的位似图形,则下列说法中错误的是( )
A.小鱼与大鱼的周长之比是1:2
B.小鱼与大鱼的对应点到位似中心的距离比是1:2
C.大鱼尾巴的面积是小鱼尾巴面积的2倍
D.若小鱼上一点的坐标是(a,b),则大鱼上的对应点的坐标是(﹣2a,﹣2b)
二.填空题(共8小题)
11.(2023秋 河东区期末)已知一元二次方程ax2﹣2x+3=0有两个实数根,则a的取值范围是 .
12.(2024春 坪山区期末)某科技公司开展技术研发,在相同条件下,对运用新技术生产的一批产品的合格率进行检测,如表是检测过程中的一组统计数据:
抽取的产品数n 500 1000 1500 2000 2500 3000 3500 4000
合格的产品数m 476 967 1431 1926 2395 2883 3367 3836
合格的产品频率 0.952 0.967 0.954 0.963 0.958 0.961 0.962 0.959
估计这批产品合格的产品的概率为 .
13.(2022秋 深圳期末)如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE= °.
14.(2024春 邓州市期末)已知反比例函数的图象在每一个象限内,y都随x的增大而减小,则k的取值范围是 .
15.(2023秋 龙泉驿区期末)如图,正方形的中心在直角坐标系的原点,正方形的边与坐标轴平行,点P(3a,a)是正方形与反比例函数图象的一个交点.已知图中阴影部分的面积等于18,则这个反比例函数的表达式为 .
16.(2024春 宿城区期末)饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中,水温y℃与开机时间x分满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降(此过程中,水温y℃与开机时间x分成反比例函数关系),当水温降至20℃时,饮水机又自动开始加热,……如此循环下去(如图所示).那么开机后56分钟时,水的温度是 ℃.
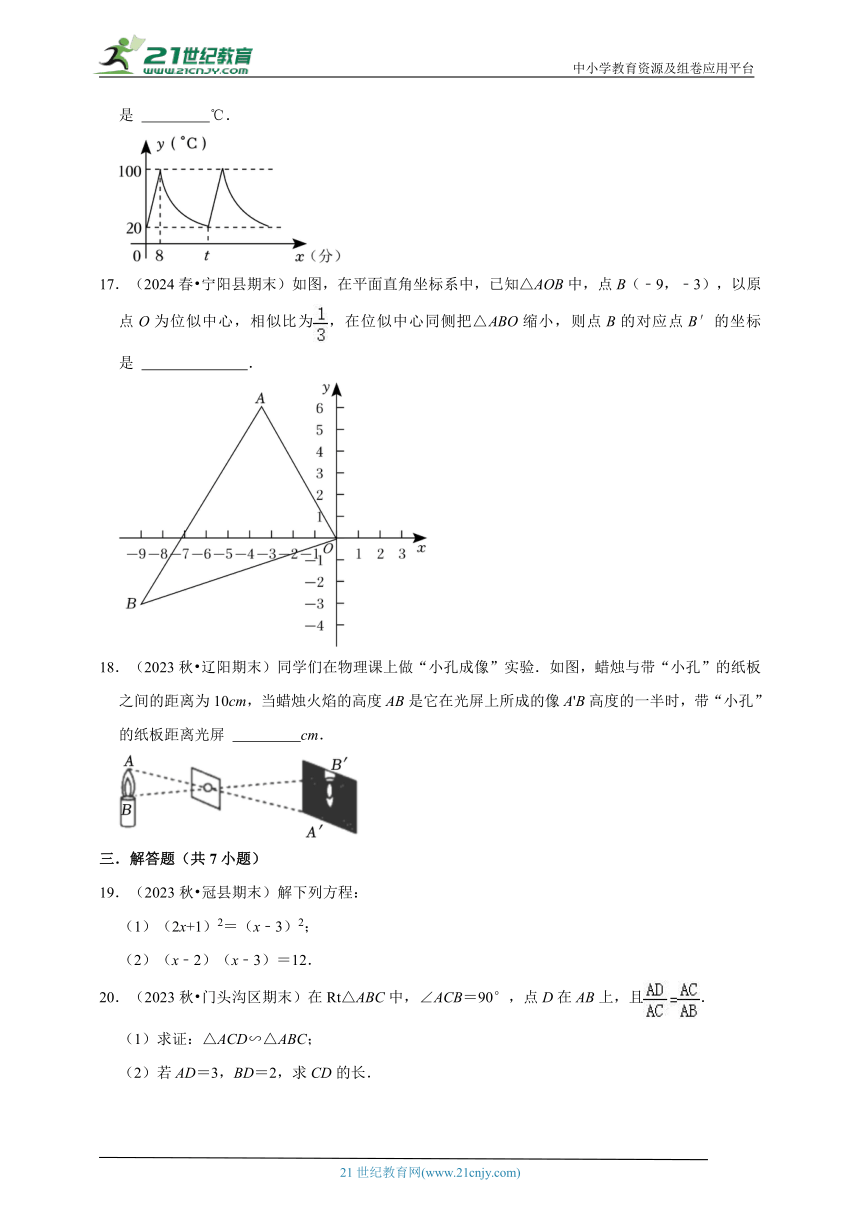
17.(2024春 宁阳县期末)如图,在平面直角坐标系中,已知△AOB中,点B(﹣9,﹣3),以原点O为位似中心,相似比为,在位似中心同侧把△ABO缩小,则点B的对应点B′的坐标是 .
18.(2023秋 辽阳期末)同学们在物理课上做“小孔成像”实验.如图,蜡烛与带“小孔”的纸板之间的距离为10cm,当蜡烛火焰的高度AB是它在光屏上所成的像A'B高度的一半时,带“小孔”的纸板距离光屏 cm.
三.解答题(共7小题)
19.(2023秋 冠县期末)解下列方程:
(1)(2x+1)2=(x﹣3)2;
(2)(x﹣2)(x﹣3)=12.
20.(2023秋 门头沟区期末)在Rt△ABC中,∠ACB=90°,点D在AB上,且.
(1)求证:△ACD∽△ABC;
(2)若AD=3,BD=2,求CD的长.
21.(2023秋 黄埔区期末)随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,现有“微信”、“支付宝”、“银行卡”和“现金”四种支付方式.
(1)若随机选一种方式进行支付,则恰巧是“现金”的概率是 ;
(2)在一次购物中,小嘉和小琪都想从“微信”、“支付宝”和“银行卡”三种支付方式中选一种方式进行支付,求出两人恰好选择同一种支付方式的概率(用画树状图法或列表法求解).
22.(2023秋 冠县期末)如图,点P是反比例函数的图象上的一点,过点P作PA⊥x轴于点A,连接OP,△AOP的面积为6.
(1)求反比例函数的解析式;
(2)若OA=4,点B是反比例函数上的点,当S△OAB=12时,直接写出点B的坐标.
23.(2023秋 乐山期末)如图,在△ABC中,AD是BC上的高,且BC=3,AD=2,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB、AC上.
(1)设EF=x(0<x<2),矩形EFGH的周长为y,求y关于x的函数解析式;(2)当EFGH为正方形时,求正方形EFGH的面积.
24.(2024春 朝阳区期末)如图,在四边形ABCD中,AB∥CD,AD∥BC,AC平分∠DAB,连接BD交AC于点O,过点C作CE⊥AB交AB延长线于点E.
(1)求证:四边形ABCD为菱形;
(2)若OA=4,OB=3,求CE的长.
25.(2021秋 金川区校级期末)如图,在平面直角坐标系中,一次函数y=x+5和y=﹣2x的图象相交于点A,反比例函数y=的图象经过点A.
(1)求反比例函数的表达式;
(2)设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积;
(3)根据图象直接写出关于x的不等式的解集.
期末重难点真题检测卷-2024-2025学年数学九年级上册北师大版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 双辽市期末)已知2a=3b(ab≠0),则下列比例式成立的是( )
A.= B.= C.= D.=
【解答】解:A、由=得ab=6,故本选项错误;
B、由=得2a=3b,故本选项正确;
C、由=得3a=2b,故本选项错误;
D、由=得3a=2b,故本选项错误.
故选:B.
2.(2023秋 静安区期末)下列选项中的两个图形一定相似的是( )
A.两个平行四边形 B.两个圆
C.两个菱形 D.两个等腰三角形
【解答】解:A.任意两个平行四边形,形状不一定相同,不一定相似,本选项不合题意;
B.任意两个圆一定相似,本选项符合题意;
C.任意两个菱形,边的比相等、对应角不一定相等,不一定相似,本选项不合题意;
D.任意两个三角形,对应角对应相等、边的比不一定相等,不一定相似,本选项不合题意;
故选:B.
3.(2023秋 宁都县期末)已知△ABC∽△DEF,且周长之比为2:3,则面积比为( )
A.2:3 B.4:9 C.9:4 D.16:81
【解答】解:∵△ABC∽△DEF,它们的周长之比为2:3,
∴三角形的相似比是2:3,
∴它们的面积之比是4:9,
故选:B.
4.(2023秋 贵阳期末)2023年12月16日,贵阳市轨道交通三号线正式运营.某校共有1000个学生,随机调查了100个学生,其中有16个学生在三号线开通首日乘坐了地铁三号线.在该校随机问一个学生,他在三号线开通首日乘坐该地铁的概率大约是( )
A.0.016 B.0.1 C.0.116 D.0.16
【解答】解:乘坐三号线地铁的频率为16÷100=0.16,
∴乘坐三号线地铁的概率大约是0.16.
故选:D.
5.(2022秋 锦江区期末)如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B的坐标是(6,2),点D的坐标是(0,2),点A在x轴上,则点C的坐标是( )
A.(3,2) B.(3,3) C.(3,4) D.(2,4)
【解答】解:连接AC,BD相交于点E,
∵四边形ABCD是菱形,
∴AE=CE,BE=DE,AC⊥BD,
∵点A在x轴上,点B的坐标为(6,2),点D的坐标为(0,2),
∴BD=6,AE=2,
∴DE=BD=3,AC=2AE=4,
∴点C的坐标为:(3,4).
故选:C.
6.(2023秋 确山县期末)若x=2是关于x的一元二次方程x2+mx﹣2=0的一个根,则m的值为( )
A.1 B.3 C.﹣1 D.﹣3
【解答】解:将x=2代入方程x2+mx﹣2=0
得:4+2m﹣2=0,解得:m=﹣1.
故选:C.
7.(2023秋 太康县期末)在如图所示的电路中,随机闭合开关S1、S2、S3中的两个,能让灯泡L1发光的概率是( )
A. B. C. D.
【解答】解:画树状图得:
∵共有6种等可能的结果,能让灯泡L1发光的有2种情况,
∴能让灯泡L1发光的概率为=.
故选:B.
8.(2023秋 息县期末)近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,某款燃油汽车2月份的售价为23万元,4月份售价为18.63万元,设该款汽车这两月售价的月平均降价率是x,可列方程正确的是( )
A.18.63(1+x)2=23 B.23(1﹣x)2=18.63
C.18.63(1﹣x)2=23 D.23(1﹣2x)=18.63
【解答】解:根据题意得:23(1﹣x)2=18.63.
故选:B.
9.(2023春 槐荫区期末)如图,点A是反比例函数在第二象限内图象上一点,点B是反比例函数在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,则△AOB的面积是( )
A.2 B.2.5 C.3 D.3.5
【解答】解:分别过A、B两点作AD⊥x轴,BE⊥x轴,垂足为D、E,
∵AC=CB,
∴OD=OE,
设A(﹣a,),则B(a,),
故S△AOB=S梯形ADEB﹣S△AOD﹣S△BOE=(+)×2a﹣a×﹣a×=3.
解法二:过A,B两点作y轴的垂线,由AC=BC求两个三角形全等,再求面积,
故选:C.
10.(2023秋 城阳区期末)如图,在平面直角坐标系中,大鱼与小鱼是关于原点O的位似图形,则下列说法中错误的是( )
A.小鱼与大鱼的周长之比是1:2
B.小鱼与大鱼的对应点到位似中心的距离比是1:2
C.大鱼尾巴的面积是小鱼尾巴面积的2倍
D.若小鱼上一点的坐标是(a,b),则大鱼上的对应点的坐标是(﹣2a,﹣2b)
【解答】解:A.大鱼与小鱼的相似比是1:2,所以A选项不符合题意;
B.小鱼与大鱼的对应点到位似中心的距离比是1:2,所以B选项不符合题意;
C.大鱼尾巴的面积是小鱼尾巴面积的4倍,所以C选项符合题意;
D.若小鱼上一点的坐标是(a,b),则在大鱼上的对应点的坐标是(﹣2a,﹣2b),所以D选项不符合题意.
故选:C.
二.填空题(共8小题)
11.(2023秋 河东区期末)已知一元二次方程ax2﹣2x+3=0有两个实数根,则a的取值范围是 a≤且a≠0 .
【解答】解:∵关于x的一元二次方程ax2﹣2x+3=0有两个实数根,
∴Δ=b2﹣4ac=(﹣2)2﹣4×a×3=4﹣12a≥0,
解得:a≤,
∵方程ax2﹣2x+3=0是一元二次方程,
∴a≠0,
∴a的取值范围是a≤且a≠0.
故答案为:a≤且a≠0.
12.(2024春 坪山区期末)某科技公司开展技术研发,在相同条件下,对运用新技术生产的一批产品的合格率进行检测,如表是检测过程中的一组统计数据:
抽取的产品数n 500 1000 1500 2000 2500 3000 3500 4000
合格的产品数m 476 967 1431 1926 2395 2883 3367 3836
合格的产品频率 0.952 0.967 0.954 0.963 0.958 0.961 0.962 0.959
估计这批产品合格的产品的概率为 0.96 .
【解答】解:由图表可知合格的产品频率都在0.95左右浮动,所以可估计这批产品合格的产品的概率为0.96,
故答案为:0.96.
13.(2022秋 深圳期末)如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE= 35 °.
【解答】解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°﹣70°)=55°,
∵DE⊥AC,
∴∠ODE=90°﹣∠DOE=20°,
∴∠CDE=∠ODC﹣∠ODE=55°﹣20°=35°;
故答案为:35.
14.(2024春 邓州市期末)已知反比例函数的图象在每一个象限内,y都随x的增大而减小,则k的取值范围是 k>1 .
【解答】解:∵在每个象限内,y随着x的增大而减小,
∴k﹣1>0,即k>1,
故答案为:k>1.
15.(2023秋 龙泉驿区期末)如图,正方形的中心在直角坐标系的原点,正方形的边与坐标轴平行,点P(3a,a)是正方形与反比例函数图象的一个交点.已知图中阴影部分的面积等于18,则这个反比例函数的表达式为 .
【解答】解:如图,∵正方形ABCD的中心在原点O,且AD∥x轴,
∴四边形AEOF为正方形,
∵点P(3a,a),
∴点A的坐标为(3a,3a),
∵正方形AEOF的面积=阴影部分的面积=18,
∴3a 3a=18,
解得a=或a=﹣(舍去),
∴P(3,),
∴k=3×=6.
∴这个反比例函数的解析式为:y=,
故答案为:y=.
16.(2024春 宿城区期末)饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中,水温y℃与开机时间x分满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降(此过程中,水温y℃与开机时间x分成反比例函数关系),当水温降至20℃时,饮水机又自动开始加热,……如此循环下去(如图所示).那么开机后56分钟时,水的温度是 50 ℃.
【解答】解:当0≤x≤8时,设水温y与开机时间x的函数关系为:y=kx+b,
依据题意,得,
解得:,
故此函数解析式为:y=10x+20;
在水温下降过程中,设水温y与开机时间x的函数关系式为:,
依据题意,得:,
解得:m=800,
∴,
当y=20时,,
解得:t=x=40,
∵56﹣40=16>8,
∴当x=16时,.
故答案为:50.
17.(2024春 宁阳县期末)如图,在平面直角坐标系中,已知△AOB中,点B(﹣9,﹣3),以原点O为位似中心,相似比为,在位似中心同侧把△ABO缩小,则点B的对应点B′的坐标是 (﹣3,﹣1) .
【解答】解:以原点O为位似中心,相似比为,在位似中心同侧把△ABO缩小,点B(﹣9,﹣3),
则点B的对应点B′的坐标为(﹣9×,﹣3×),即点B′的坐标为(﹣3,﹣1),
故答案为:(﹣3,﹣1).
18.(2023秋 辽阳期末)同学们在物理课上做“小孔成像”实验.如图,蜡烛与带“小孔”的纸板之间的距离为10cm,当蜡烛火焰的高度AB是它在光屏上所成的像A'B高度的一半时,带“小孔”的纸板距离光屏 20 cm.
【解答】解:设带“小孔”的纸板距离光屏是x,
根据题意可得:,
解得:x=20,
经检验x=20是原方程的解,
则带“小孔”的纸板距离光屏是20cm,
故答案为:20.
三.解答题(共7小题)
19.(2023秋 冠县期末)解下列方程:
(1)(2x+1)2=(x﹣3)2;
(2)(x﹣2)(x﹣3)=12.
【解答】解:(1)(2x+1)2=(x﹣3)2,
(2x+1)2﹣(x﹣3)2=0,
(,2x+1+x﹣3)(2x+1﹣x+3)=0,
(3x﹣2)(x+4)=0,
3x﹣2=0或x+4=0,
∴,x2=﹣4;
(2)∵(x﹣2)(x﹣3)=12,
∴x2﹣5x﹣6=0,
∴(x﹣6)(x+1)=0,
∴x﹣6=0或x+1=0,
∴x1=6,x2=﹣1.
20.(2023秋 门头沟区期末)在Rt△ABC中,∠ACB=90°,点D在AB上,且.
(1)求证:△ACD∽△ABC;
(2)若AD=3,BD=2,求CD的长.
【解答】(1)证明:∵=,∠A=∠A,
∴△ACD∽△ABC;
(2)解:∵△ACD∽△ABC,
∴∠ACD=∠B,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴∠ADC=∠BDC,
∵∠ACD=∠B,
∴△ACD∽△CBD,
∴=,
∴=,
∴CD=.
21.(2023秋 黄埔区期末)随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,现有“微信”、“支付宝”、“银行卡”和“现金”四种支付方式.
(1)若随机选一种方式进行支付,则恰巧是“现金”的概率是 ;
(2)在一次购物中,小嘉和小琪都想从“微信”、“支付宝”和“银行卡”三种支付方式中选一种方式进行支付,求出两人恰好选择同一种支付方式的概率(用画树状图法或列表法求解).
【解答】解:(1)若随机选一种方式进行支付,则恰巧是“现金”支付方式的概率为,
故答案为;
(2)树状图如图,由树状图可知,共有9种等可能结果,其中两人恰好选择同一种支付方式的有3种,故P(两人恰好选择同一种支付方式)为.
22.(2023秋 冠县期末)如图,点P是反比例函数的图象上的一点,过点P作PA⊥x轴于点A,连接OP,△AOP的面积为6.
(1)求反比例函数的解析式;
(2)若OA=4,点B是反比例函数上的点,当S△OAB=12时,直接写出点B的坐标.
【解答】解:(1)由于P为反比例函数y=的图象上一点,
∴S△AOP=|k|=6,
又∵函数位于第二象限,
∴k=﹣12,
∴反比例函数的解析式为y=﹣;
(2)设点B(a,﹣),
∵OA=4,S△OAB=12,
∴×4×|﹣|=12,
∴a=±2,
∵点B在第二象限,
∴点B(﹣2,6).
23.(2023秋 乐山期末)如图,在△ABC中,AD是BC上的高,且BC=3,AD=2,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB、AC上.
(1)设EF=x(0<x<2),矩形EFGH的周长为y,求y关于x的函数解析式;(2)当EFGH为正方形时,求正方形EFGH的面积.
【解答】解:(1)设AD与EH的交点为M,
∵四边形EFGH是矩形,
∴EH∥BC,
∴△AEH∽△ABC,
∴,
∵EF=DM=x,AD=2,
∴AM=2﹣x,
∴,
∴EH=(2﹣x),
∴y=2(EF+EH)=2x+6﹣3x=6﹣x(0<x<2);
(2)∵EFGH为正方形,
∴EF=EH,
∴x=(2﹣x),
∴x=,
∴EF=,
∴正方形EFGH的面积=.
24.(2024春 朝阳区期末)如图,在四边形ABCD中,AB∥CD,AD∥BC,AC平分∠DAB,连接BD交AC于点O,过点C作CE⊥AB交AB延长线于点E.
(1)求证:四边形ABCD为菱形;
(2)若OA=4,OB=3,求CE的长.
【解答】(1)证明:∵AB∥CD,AD∥BC,
∴∠BAC=∠DCA,四边形ABCD是平行四边形,
∵AC平分∠DAB,
∴∠BAC=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,OA=4,OB=3,
∴AC⊥BD,AC=2OA=8,BD=2OB=6,
∴∠AOB=90°,
∴AB===5,
∵CE⊥AB,
∴S菱形ABCD=AB CE=AC BD,
即5CE=×8×6,
解得:CE=,
即CE的长为.
25.(2021秋 金川区校级期末)如图,在平面直角坐标系中,一次函数y=x+5和y=﹣2x的图象相交于点A,反比例函数y=的图象经过点A.
(1)求反比例函数的表达式;
(2)设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积;
(3)根据图象直接写出关于x的不等式的解集.
【解答】解:(1)联立,解得,
∴A点坐标为(﹣2,4).
将A(﹣2,4)代入y=,得4=.
∴k=﹣8.
∴反比例函数的表达式为y=﹣;
(2)联立,解得或.
∴B(﹣8,1).
在y=x+5中,令y=0,得x=﹣10.
故直线AB与x轴的交点为C(﹣10,0).
如图,过A、B两点分别作x轴的垂线,交x轴于M、N两点,
则S△AOB=S△AOC﹣S△BOC= OC AM﹣ OC BN=×10×4﹣×10×1=15.
(3)关于x的不等式的解集为﹣8<x<﹣2或x>0.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末重难点真题检测卷-2024-2025学年数学九年级上册北师大版
一.选择题(共10小题)
1.(2023秋 双辽市期末)已知2a=3b(ab≠0),则下列比例式成立的是( )
A.= B.= C.= D.=
2.(2023秋 静安区期末)下列选项中的两个图形一定相似的是( )
A.两个平行四边形 B.两个圆
C.两个菱形 D.两个等腰三角形
3.(2023秋 宁都县期末)已知△ABC∽△DEF,且周长之比为2:3,则面积比为( )
A.2:3 B.4:9 C.9:4 D.16:81
4.(2023秋 贵阳期末)2023年12月16日,贵阳市轨道交通三号线正式运营.某校共有1000个学生,随机调查了100个学生,其中有16个学生在三号线开通首日乘坐了地铁三号线.在该校随机问一个学生,他在三号线开通首日乘坐该地铁的概率大约是( )
A.0.016 B.0.1 C.0.116 D.0.16
5.(2022秋 锦江区期末)如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B的坐标是(6,2),点D的坐标是(0,2),点A在x轴上,则点C的坐标是( )
A.(3,2) B.(3,3) C.(3,4) D.(2,4)
6.(2023秋 确山县期末)若x=2是关于x的一元二次方程x2+mx﹣2=0的一个根,则m的值为( )
A.1 B.3 C.﹣1 D.﹣3
7.(2023秋 太康县期末)在如图所示的电路中,随机闭合开关S1、S2、S3中的两个,能让灯泡L1发光的概率是( )
A. B. C. D.
8.(2023秋 息县期末)近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,某款燃油汽车2月份的售价为23万元,4月份售价为18.63万元,设该款汽车这两月售价的月平均降价率是x,可列方程正确的是( )
A.18.63(1+x)2=23 B.23(1﹣x)2=18.63
C.18.63(1﹣x)2=23 D.23(1﹣2x)=18.63
9.(2023春 槐荫区期末)如图,点A是反比例函数在第二象限内图象上一点,点B是反比例函数在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,则△AOB的面积是( )
A.2 B.2.5 C.3 D.3.5
10.(2023秋 城阳区期末)如图,在平面直角坐标系中,大鱼与小鱼是关于原点O的位似图形,则下列说法中错误的是( )
A.小鱼与大鱼的周长之比是1:2
B.小鱼与大鱼的对应点到位似中心的距离比是1:2
C.大鱼尾巴的面积是小鱼尾巴面积的2倍
D.若小鱼上一点的坐标是(a,b),则大鱼上的对应点的坐标是(﹣2a,﹣2b)
二.填空题(共8小题)
11.(2023秋 河东区期末)已知一元二次方程ax2﹣2x+3=0有两个实数根,则a的取值范围是 .
12.(2024春 坪山区期末)某科技公司开展技术研发,在相同条件下,对运用新技术生产的一批产品的合格率进行检测,如表是检测过程中的一组统计数据:
抽取的产品数n 500 1000 1500 2000 2500 3000 3500 4000
合格的产品数m 476 967 1431 1926 2395 2883 3367 3836
合格的产品频率 0.952 0.967 0.954 0.963 0.958 0.961 0.962 0.959
估计这批产品合格的产品的概率为 .
13.(2022秋 深圳期末)如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE= °.
14.(2024春 邓州市期末)已知反比例函数的图象在每一个象限内,y都随x的增大而减小,则k的取值范围是 .
15.(2023秋 龙泉驿区期末)如图,正方形的中心在直角坐标系的原点,正方形的边与坐标轴平行,点P(3a,a)是正方形与反比例函数图象的一个交点.已知图中阴影部分的面积等于18,则这个反比例函数的表达式为 .
16.(2024春 宿城区期末)饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中,水温y℃与开机时间x分满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降(此过程中,水温y℃与开机时间x分成反比例函数关系),当水温降至20℃时,饮水机又自动开始加热,……如此循环下去(如图所示).那么开机后56分钟时,水的温度是 ℃.
17.(2024春 宁阳县期末)如图,在平面直角坐标系中,已知△AOB中,点B(﹣9,﹣3),以原点O为位似中心,相似比为,在位似中心同侧把△ABO缩小,则点B的对应点B′的坐标是 .
18.(2023秋 辽阳期末)同学们在物理课上做“小孔成像”实验.如图,蜡烛与带“小孔”的纸板之间的距离为10cm,当蜡烛火焰的高度AB是它在光屏上所成的像A'B高度的一半时,带“小孔”的纸板距离光屏 cm.
三.解答题(共7小题)
19.(2023秋 冠县期末)解下列方程:
(1)(2x+1)2=(x﹣3)2;
(2)(x﹣2)(x﹣3)=12.
20.(2023秋 门头沟区期末)在Rt△ABC中,∠ACB=90°,点D在AB上,且.
(1)求证:△ACD∽△ABC;
(2)若AD=3,BD=2,求CD的长.
21.(2023秋 黄埔区期末)随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,现有“微信”、“支付宝”、“银行卡”和“现金”四种支付方式.
(1)若随机选一种方式进行支付,则恰巧是“现金”的概率是 ;
(2)在一次购物中,小嘉和小琪都想从“微信”、“支付宝”和“银行卡”三种支付方式中选一种方式进行支付,求出两人恰好选择同一种支付方式的概率(用画树状图法或列表法求解).
22.(2023秋 冠县期末)如图,点P是反比例函数的图象上的一点,过点P作PA⊥x轴于点A,连接OP,△AOP的面积为6.
(1)求反比例函数的解析式;
(2)若OA=4,点B是反比例函数上的点,当S△OAB=12时,直接写出点B的坐标.
23.(2023秋 乐山期末)如图,在△ABC中,AD是BC上的高,且BC=3,AD=2,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB、AC上.
(1)设EF=x(0<x<2),矩形EFGH的周长为y,求y关于x的函数解析式;(2)当EFGH为正方形时,求正方形EFGH的面积.
24.(2024春 朝阳区期末)如图,在四边形ABCD中,AB∥CD,AD∥BC,AC平分∠DAB,连接BD交AC于点O,过点C作CE⊥AB交AB延长线于点E.
(1)求证:四边形ABCD为菱形;
(2)若OA=4,OB=3,求CE的长.
25.(2021秋 金川区校级期末)如图,在平面直角坐标系中,一次函数y=x+5和y=﹣2x的图象相交于点A,反比例函数y=的图象经过点A.
(1)求反比例函数的表达式;
(2)设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积;
(3)根据图象直接写出关于x的不等式的解集.
期末重难点真题检测卷-2024-2025学年数学九年级上册北师大版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 双辽市期末)已知2a=3b(ab≠0),则下列比例式成立的是( )
A.= B.= C.= D.=
【解答】解:A、由=得ab=6,故本选项错误;
B、由=得2a=3b,故本选项正确;
C、由=得3a=2b,故本选项错误;
D、由=得3a=2b,故本选项错误.
故选:B.
2.(2023秋 静安区期末)下列选项中的两个图形一定相似的是( )
A.两个平行四边形 B.两个圆
C.两个菱形 D.两个等腰三角形
【解答】解:A.任意两个平行四边形,形状不一定相同,不一定相似,本选项不合题意;
B.任意两个圆一定相似,本选项符合题意;
C.任意两个菱形,边的比相等、对应角不一定相等,不一定相似,本选项不合题意;
D.任意两个三角形,对应角对应相等、边的比不一定相等,不一定相似,本选项不合题意;
故选:B.
3.(2023秋 宁都县期末)已知△ABC∽△DEF,且周长之比为2:3,则面积比为( )
A.2:3 B.4:9 C.9:4 D.16:81
【解答】解:∵△ABC∽△DEF,它们的周长之比为2:3,
∴三角形的相似比是2:3,
∴它们的面积之比是4:9,
故选:B.
4.(2023秋 贵阳期末)2023年12月16日,贵阳市轨道交通三号线正式运营.某校共有1000个学生,随机调查了100个学生,其中有16个学生在三号线开通首日乘坐了地铁三号线.在该校随机问一个学生,他在三号线开通首日乘坐该地铁的概率大约是( )
A.0.016 B.0.1 C.0.116 D.0.16
【解答】解:乘坐三号线地铁的频率为16÷100=0.16,
∴乘坐三号线地铁的概率大约是0.16.
故选:D.
5.(2022秋 锦江区期末)如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B的坐标是(6,2),点D的坐标是(0,2),点A在x轴上,则点C的坐标是( )
A.(3,2) B.(3,3) C.(3,4) D.(2,4)
【解答】解:连接AC,BD相交于点E,
∵四边形ABCD是菱形,
∴AE=CE,BE=DE,AC⊥BD,
∵点A在x轴上,点B的坐标为(6,2),点D的坐标为(0,2),
∴BD=6,AE=2,
∴DE=BD=3,AC=2AE=4,
∴点C的坐标为:(3,4).
故选:C.
6.(2023秋 确山县期末)若x=2是关于x的一元二次方程x2+mx﹣2=0的一个根,则m的值为( )
A.1 B.3 C.﹣1 D.﹣3
【解答】解:将x=2代入方程x2+mx﹣2=0
得:4+2m﹣2=0,解得:m=﹣1.
故选:C.
7.(2023秋 太康县期末)在如图所示的电路中,随机闭合开关S1、S2、S3中的两个,能让灯泡L1发光的概率是( )
A. B. C. D.
【解答】解:画树状图得:
∵共有6种等可能的结果,能让灯泡L1发光的有2种情况,
∴能让灯泡L1发光的概率为=.
故选:B.
8.(2023秋 息县期末)近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,某款燃油汽车2月份的售价为23万元,4月份售价为18.63万元,设该款汽车这两月售价的月平均降价率是x,可列方程正确的是( )
A.18.63(1+x)2=23 B.23(1﹣x)2=18.63
C.18.63(1﹣x)2=23 D.23(1﹣2x)=18.63
【解答】解:根据题意得:23(1﹣x)2=18.63.
故选:B.
9.(2023春 槐荫区期末)如图,点A是反比例函数在第二象限内图象上一点,点B是反比例函数在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,则△AOB的面积是( )
A.2 B.2.5 C.3 D.3.5
【解答】解:分别过A、B两点作AD⊥x轴,BE⊥x轴,垂足为D、E,
∵AC=CB,
∴OD=OE,
设A(﹣a,),则B(a,),
故S△AOB=S梯形ADEB﹣S△AOD﹣S△BOE=(+)×2a﹣a×﹣a×=3.
解法二:过A,B两点作y轴的垂线,由AC=BC求两个三角形全等,再求面积,
故选:C.
10.(2023秋 城阳区期末)如图,在平面直角坐标系中,大鱼与小鱼是关于原点O的位似图形,则下列说法中错误的是( )
A.小鱼与大鱼的周长之比是1:2
B.小鱼与大鱼的对应点到位似中心的距离比是1:2
C.大鱼尾巴的面积是小鱼尾巴面积的2倍
D.若小鱼上一点的坐标是(a,b),则大鱼上的对应点的坐标是(﹣2a,﹣2b)
【解答】解:A.大鱼与小鱼的相似比是1:2,所以A选项不符合题意;
B.小鱼与大鱼的对应点到位似中心的距离比是1:2,所以B选项不符合题意;
C.大鱼尾巴的面积是小鱼尾巴面积的4倍,所以C选项符合题意;
D.若小鱼上一点的坐标是(a,b),则在大鱼上的对应点的坐标是(﹣2a,﹣2b),所以D选项不符合题意.
故选:C.
二.填空题(共8小题)
11.(2023秋 河东区期末)已知一元二次方程ax2﹣2x+3=0有两个实数根,则a的取值范围是 a≤且a≠0 .
【解答】解:∵关于x的一元二次方程ax2﹣2x+3=0有两个实数根,
∴Δ=b2﹣4ac=(﹣2)2﹣4×a×3=4﹣12a≥0,
解得:a≤,
∵方程ax2﹣2x+3=0是一元二次方程,
∴a≠0,
∴a的取值范围是a≤且a≠0.
故答案为:a≤且a≠0.
12.(2024春 坪山区期末)某科技公司开展技术研发,在相同条件下,对运用新技术生产的一批产品的合格率进行检测,如表是检测过程中的一组统计数据:
抽取的产品数n 500 1000 1500 2000 2500 3000 3500 4000
合格的产品数m 476 967 1431 1926 2395 2883 3367 3836
合格的产品频率 0.952 0.967 0.954 0.963 0.958 0.961 0.962 0.959
估计这批产品合格的产品的概率为 0.96 .
【解答】解:由图表可知合格的产品频率都在0.95左右浮动,所以可估计这批产品合格的产品的概率为0.96,
故答案为:0.96.
13.(2022秋 深圳期末)如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE= 35 °.
【解答】解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°﹣70°)=55°,
∵DE⊥AC,
∴∠ODE=90°﹣∠DOE=20°,
∴∠CDE=∠ODC﹣∠ODE=55°﹣20°=35°;
故答案为:35.
14.(2024春 邓州市期末)已知反比例函数的图象在每一个象限内,y都随x的增大而减小,则k的取值范围是 k>1 .
【解答】解:∵在每个象限内,y随着x的增大而减小,
∴k﹣1>0,即k>1,
故答案为:k>1.
15.(2023秋 龙泉驿区期末)如图,正方形的中心在直角坐标系的原点,正方形的边与坐标轴平行,点P(3a,a)是正方形与反比例函数图象的一个交点.已知图中阴影部分的面积等于18,则这个反比例函数的表达式为 .
【解答】解:如图,∵正方形ABCD的中心在原点O,且AD∥x轴,
∴四边形AEOF为正方形,
∵点P(3a,a),
∴点A的坐标为(3a,3a),
∵正方形AEOF的面积=阴影部分的面积=18,
∴3a 3a=18,
解得a=或a=﹣(舍去),
∴P(3,),
∴k=3×=6.
∴这个反比例函数的解析式为:y=,
故答案为:y=.
16.(2024春 宿城区期末)饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中,水温y℃与开机时间x分满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降(此过程中,水温y℃与开机时间x分成反比例函数关系),当水温降至20℃时,饮水机又自动开始加热,……如此循环下去(如图所示).那么开机后56分钟时,水的温度是 50 ℃.
【解答】解:当0≤x≤8时,设水温y与开机时间x的函数关系为:y=kx+b,
依据题意,得,
解得:,
故此函数解析式为:y=10x+20;
在水温下降过程中,设水温y与开机时间x的函数关系式为:,
依据题意,得:,
解得:m=800,
∴,
当y=20时,,
解得:t=x=40,
∵56﹣40=16>8,
∴当x=16时,.
故答案为:50.
17.(2024春 宁阳县期末)如图,在平面直角坐标系中,已知△AOB中,点B(﹣9,﹣3),以原点O为位似中心,相似比为,在位似中心同侧把△ABO缩小,则点B的对应点B′的坐标是 (﹣3,﹣1) .
【解答】解:以原点O为位似中心,相似比为,在位似中心同侧把△ABO缩小,点B(﹣9,﹣3),
则点B的对应点B′的坐标为(﹣9×,﹣3×),即点B′的坐标为(﹣3,﹣1),
故答案为:(﹣3,﹣1).
18.(2023秋 辽阳期末)同学们在物理课上做“小孔成像”实验.如图,蜡烛与带“小孔”的纸板之间的距离为10cm,当蜡烛火焰的高度AB是它在光屏上所成的像A'B高度的一半时,带“小孔”的纸板距离光屏 20 cm.
【解答】解:设带“小孔”的纸板距离光屏是x,
根据题意可得:,
解得:x=20,
经检验x=20是原方程的解,
则带“小孔”的纸板距离光屏是20cm,
故答案为:20.
三.解答题(共7小题)
19.(2023秋 冠县期末)解下列方程:
(1)(2x+1)2=(x﹣3)2;
(2)(x﹣2)(x﹣3)=12.
【解答】解:(1)(2x+1)2=(x﹣3)2,
(2x+1)2﹣(x﹣3)2=0,
(,2x+1+x﹣3)(2x+1﹣x+3)=0,
(3x﹣2)(x+4)=0,
3x﹣2=0或x+4=0,
∴,x2=﹣4;
(2)∵(x﹣2)(x﹣3)=12,
∴x2﹣5x﹣6=0,
∴(x﹣6)(x+1)=0,
∴x﹣6=0或x+1=0,
∴x1=6,x2=﹣1.
20.(2023秋 门头沟区期末)在Rt△ABC中,∠ACB=90°,点D在AB上,且.
(1)求证:△ACD∽△ABC;
(2)若AD=3,BD=2,求CD的长.
【解答】(1)证明:∵=,∠A=∠A,
∴△ACD∽△ABC;
(2)解:∵△ACD∽△ABC,
∴∠ACD=∠B,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴∠ADC=∠BDC,
∵∠ACD=∠B,
∴△ACD∽△CBD,
∴=,
∴=,
∴CD=.
21.(2023秋 黄埔区期末)随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,现有“微信”、“支付宝”、“银行卡”和“现金”四种支付方式.
(1)若随机选一种方式进行支付,则恰巧是“现金”的概率是 ;
(2)在一次购物中,小嘉和小琪都想从“微信”、“支付宝”和“银行卡”三种支付方式中选一种方式进行支付,求出两人恰好选择同一种支付方式的概率(用画树状图法或列表法求解).
【解答】解:(1)若随机选一种方式进行支付,则恰巧是“现金”支付方式的概率为,
故答案为;
(2)树状图如图,由树状图可知,共有9种等可能结果,其中两人恰好选择同一种支付方式的有3种,故P(两人恰好选择同一种支付方式)为.
22.(2023秋 冠县期末)如图,点P是反比例函数的图象上的一点,过点P作PA⊥x轴于点A,连接OP,△AOP的面积为6.
(1)求反比例函数的解析式;
(2)若OA=4,点B是反比例函数上的点,当S△OAB=12时,直接写出点B的坐标.
【解答】解:(1)由于P为反比例函数y=的图象上一点,
∴S△AOP=|k|=6,
又∵函数位于第二象限,
∴k=﹣12,
∴反比例函数的解析式为y=﹣;
(2)设点B(a,﹣),
∵OA=4,S△OAB=12,
∴×4×|﹣|=12,
∴a=±2,
∵点B在第二象限,
∴点B(﹣2,6).
23.(2023秋 乐山期末)如图,在△ABC中,AD是BC上的高,且BC=3,AD=2,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB、AC上.
(1)设EF=x(0<x<2),矩形EFGH的周长为y,求y关于x的函数解析式;(2)当EFGH为正方形时,求正方形EFGH的面积.
【解答】解:(1)设AD与EH的交点为M,
∵四边形EFGH是矩形,
∴EH∥BC,
∴△AEH∽△ABC,
∴,
∵EF=DM=x,AD=2,
∴AM=2﹣x,
∴,
∴EH=(2﹣x),
∴y=2(EF+EH)=2x+6﹣3x=6﹣x(0<x<2);
(2)∵EFGH为正方形,
∴EF=EH,
∴x=(2﹣x),
∴x=,
∴EF=,
∴正方形EFGH的面积=.
24.(2024春 朝阳区期末)如图,在四边形ABCD中,AB∥CD,AD∥BC,AC平分∠DAB,连接BD交AC于点O,过点C作CE⊥AB交AB延长线于点E.
(1)求证:四边形ABCD为菱形;
(2)若OA=4,OB=3,求CE的长.
【解答】(1)证明:∵AB∥CD,AD∥BC,
∴∠BAC=∠DCA,四边形ABCD是平行四边形,
∵AC平分∠DAB,
∴∠BAC=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,OA=4,OB=3,
∴AC⊥BD,AC=2OA=8,BD=2OB=6,
∴∠AOB=90°,
∴AB===5,
∵CE⊥AB,
∴S菱形ABCD=AB CE=AC BD,
即5CE=×8×6,
解得:CE=,
即CE的长为.
25.(2021秋 金川区校级期末)如图,在平面直角坐标系中,一次函数y=x+5和y=﹣2x的图象相交于点A,反比例函数y=的图象经过点A.
(1)求反比例函数的表达式;
(2)设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积;
(3)根据图象直接写出关于x的不等式的解集.
【解答】解:(1)联立,解得,
∴A点坐标为(﹣2,4).
将A(﹣2,4)代入y=,得4=.
∴k=﹣8.
∴反比例函数的表达式为y=﹣;
(2)联立,解得或.
∴B(﹣8,1).
在y=x+5中,令y=0,得x=﹣10.
故直线AB与x轴的交点为C(﹣10,0).
如图,过A、B两点分别作x轴的垂线,交x轴于M、N两点,
则S△AOB=S△AOC﹣S△BOC= OC AM﹣ OC BN=×10×4﹣×10×1=15.
(3)关于x的不等式的解集为﹣8<x<﹣2或x>0.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
