期末真题重组卷-2024-2025学年数学八年级上册苏科版(含解析)
文档属性
| 名称 | 期末真题重组卷-2024-2025学年数学八年级上册苏科版(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 840.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 14:20:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组卷-2024-2025学年数学八年级上册苏科版
一.选择题(共10小题)
1.(2023秋 宁乡市期末)平面直角坐标系中,点P(2,3)关于x轴对称的点的坐标是( )
A.(2,3) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
2.(2023秋 槐荫区期末)的相反数是( )
A.﹣ B.± C.﹣5 D.5
3.(2023秋 怀集县期末)下列四个数字图形,是轴对称图形的是( )
A. B. C. D.
4.(2023秋 全椒县期末)如图,点E、H、G、N共线,∠E=∠N,EF=NM,添加一个条件,不能判断△EFG≌△NMH的是( )
A.EH=NG B.∠F=∠M C.FG=MH D.FG∥HM
5.(2023秋 连山区期末)如图,△ABC≌△DEF,点A与点D是对应点,点C与点F是对应点,则∠E等于( )
A.30° B.50° C.60° D.100°
6.(2023秋 丹江口市期末)如图,在△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,连接MD,过点D作DN⊥MD,交BM于点N.CD与BM相交于点E,若点E是CD的中点,则下列结论:①AC=BE;②DM=DN;③∠AMD=45°;④NE=3ME.其中正确的有( )个.
A.4 B.3 C.2 D.1
7.(2023秋 罗湖区校级期末)如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=3,则CE2+CF2的值为( )
A.6 B.9 C.18 D.36
8.(2023秋 郏县期末)如图,直线l1:y=x+2与直线l2:y=kx+b相交于点P(m,4),则方程组的解是( )
A. B. C. D.
9.(2023秋 金东区期末)如图,是由四个全等的直角三角形拼成的“赵爽弦图”,得到正方形ABCD与正方形EFGH,连结DF.若S正方形ABCD=5,EF=BG,则DF的长为( )
A.2 B. C.3 D.
10.(2023秋 法库县期末)一列动车从A地开往B地,一列普通列车从B地开往A地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示y与x之间的函数关系.下列叙述错误的是( )
A.AB两地相距1000千米
B.两车出发后3小时相遇
C.动车的速度为千米/时
D.普通列车行驶t小时后,动车到达终点B地,此时普通列车还需行驶千米到达A地
二.填空题(共8小题)
11.(2024秋 揭西县期中)平面直角坐标系中,若点P(4﹣m,3+m)在x轴上,则点P的坐标为 ;
12.(2024秋 江阴市期中)如图,AC⊥BC,AD⊥BD,垂足分别为C、D,请你添加一个条件 ,使得△ABD≌△BAC.
13.(2024秋 营口期中)如图,△ABC的边AB的垂直平分线交AC于点D,连结BD,若BD=5,AC=12,则DC= .
14.(2024秋 成都期中)如图,长方形ABCD中,AB=3,BC=1,AB在数轴上,以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为 .
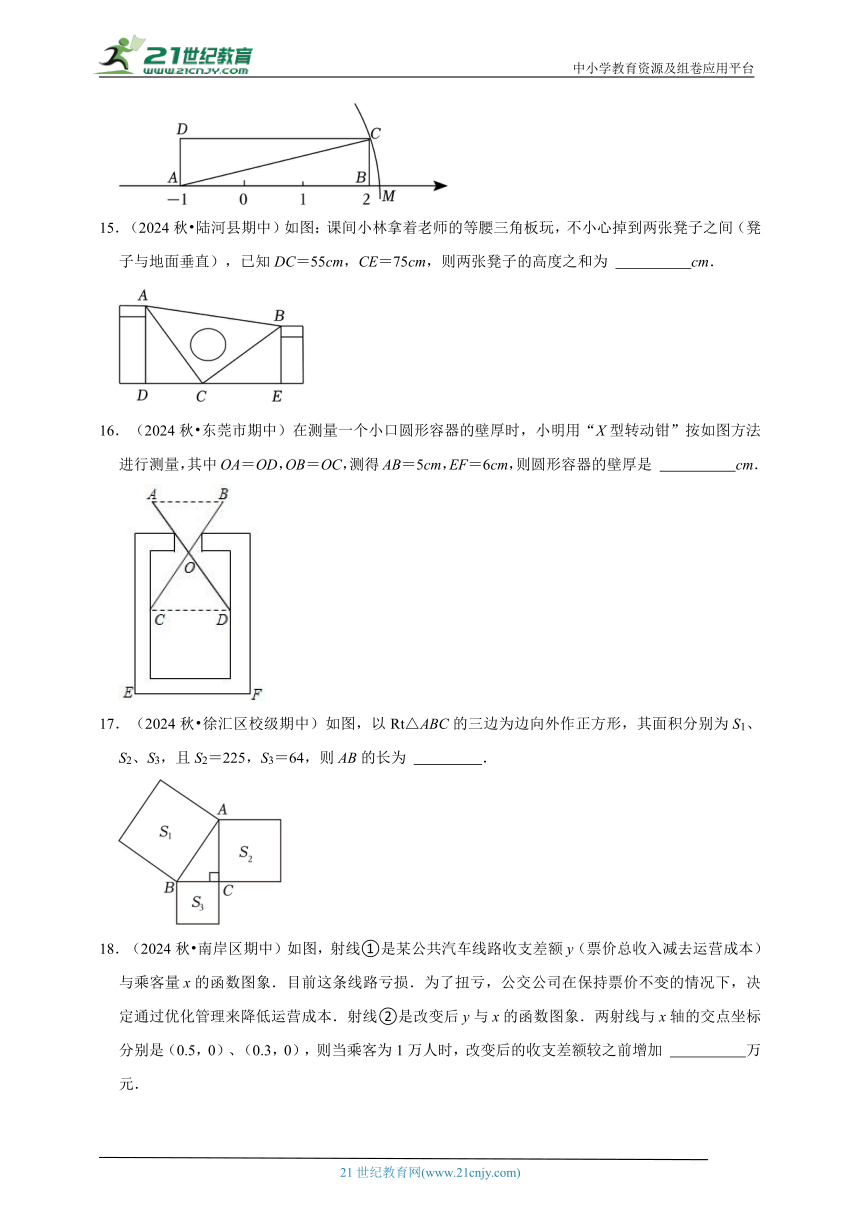
15.(2024秋 陆河县期中)如图:课间小林拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知DC=55cm,CE=75cm,则两张凳子的高度之和为 cm.
16.(2024秋 东莞市期中)在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=5cm,EF=6cm,则圆形容器的壁厚是 cm.
17.(2024秋 徐汇区校级期中)如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S2=225,S3=64,则AB的长为 .
18.(2024秋 南岸区期中)如图,射线①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象.目前这条线路亏损.为了扭亏,公交公司在保持票价不变的情况下,决定通过优化管理来降低运营成本.射线②是改变后y与x的函数图象.两射线与x轴的交点坐标分别是(0.5,0)、(0.3,0),则当乘客为1万人时,改变后的收支差额较之前增加 万元.
三.解答题(共8小题)
19.(2024秋 东港市期中)计算:
(1)
(2).
20.(2024秋 海淀区校级期中)已知:如图,点B,F,C,E在同一条直线上,AB∥DE,AB=DE,∠A=∠D.求证:△ABC≌△DEF.
21.(2024秋 浙江期中)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,交AC于点D,连结EC.
(1)求∠ECB的度数;
(2)若CE=4,求BC长.
22.(2024秋 东城区校级期中)如图1,△ABC与△DBC全等,且∠ACB=∠DBC=90°,BC=6,AC=4.如图2,将△DBC沿射线BC方向平移得到△D1B1C1,连接AC1,BD1.
(1)求证:BD1=AC1且BD1∥AC1;
(2)△DBC沿射线BC方向平移的距离等于 时,点A与点D1之间的距离最小.
23.(2024秋 拜城县期中)荡秋千一直以来都是深受小朋友们喜爱的娱乐项目,周六,丽丽与爸爸妈妈在公园里荡秋千.如图,丽丽坐在秋千的起始位置点A处,OA与地面垂直并交于点M,两脚在地面上用力一蹬,妈妈在点B处接住她后用力一推,爸爸在点C处接住她.若妈妈与爸爸到OA的水平距离BD,CE分别为1.4m和1.8m,∠BOC=90°,求DE的长.
24.(2024春 大同期末)消防云梯主要用于高层建筑火灾等救援任务,它能让消防员快速到达高层建筑的火灾现场,执行灭火、疏散等救援任务.如图,已知云梯最多能伸长到25m(AA′=BB′=25m),消防车高4m.某次任务中,消防车在A处将云梯伸长至最长,消防员从19m(A′M=19m)高的A′处救人后,消防车需到达B处使消防员从24m(B′M=24m)高的B′处救人,求消防车从A处向着火的楼房靠近的距离AB.
25.(2023秋 庆云县期末)如图①,油纸伞是中国传统工艺品之一,起源于中国的一种纸制或布制伞.油纸伞的制作工艺十分巧妙,如图②,伞圈D沿着伞柄AP滑动时,伞柄AP始终平分同一平面内两条伞骨所成的∠BAC,伞骨BD,CD的B,C点固定不动,且到点A的距离AB=AC.
(1)当D点在伞柄AP上滑动时,处于同一平面的两条伞骨BD和CD相等吗?请说明理由.
(2)如图③,当油纸伞撑开时,伞的边缘M,N与点D在同一直线上,若∠BAC=140°,∠MBD=120°,求∠CDA的度数.
26.(2024秋 江北区校级期中)如图1,△ABC是直角三角形,∠C=90°,BC=4,AC=3,点P从点B出发,以每秒1个单位长度的速度沿着B﹣C﹣A方向运动到A点停止,设y=S△ABP,点P的运动时间为x秒.
(1)直接写出y与x之间的函数表达式,并写出对应x的取值范围.
(2)在平面直角坐标系中画出y的图象,并写出y的一条性质.
(3)结合作出的图象直接写出它与函数y=x+1相交时x的值.(保留一位小数,误差不超过0.2)
期末真题重组卷-2024-2025学年数学八年级上册苏科版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 宁乡市期末)平面直角坐标系中,点P(2,3)关于x轴对称的点的坐标是( )
A.(2,3) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
【解答】解:点P(2,3)关于x轴对称的点的坐标为(2,﹣3).
故选:C.
2.(2023秋 槐荫区期末)的相反数是( )
A.﹣ B.± C.﹣5 D.5
【解答】解:的相反数是﹣,
故选:A.
3.(2023秋 怀集县期末)下列四个数字图形,是轴对称图形的是( )
A. B. C. D.
【解答】解:A、是中心对称图形,故本选项不符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、是轴对称图形,故本选项符合题意.
故选:D.
4.(2023秋 全椒县期末)如图,点E、H、G、N共线,∠E=∠N,EF=NM,添加一个条件,不能判断△EFG≌△NMH的是( )
A.EH=NG B.∠F=∠M C.FG=MH D.FG∥HM
【解答】解:在△EFG与△NMH中,已知,∠E=∠N,EF=NM,
A.由EH=NG可得EG=NH,所以添加条件EH=NG,根据SAS可证△EFG≌△NMH,故本选项不符合题意;
B.添加条件∠F=∠M,根据ASA可证△EFG≌△NMH,故本选项不符合题意;
C.添加条件FG=MH,不能证明△EFG≌△NMH,故本选项符合题意;
D.由FG∥HM可得∠EGF=∠NHM,所以添加条件FG∥HM,根据AAS可证△EFG≌△NMH,故本选项不符合题意;
故选:C.
5.(2023秋 连山区期末)如图,△ABC≌△DEF,点A与点D是对应点,点C与点F是对应点,则∠E等于( )
A.30° B.50° C.60° D.100°
【解答】解:∵△ABC≌△DEF,
∴∠D=∠A=50°,
∴∠E=180°﹣∠D﹣∠F=30°,
故选:A.
6.(2023秋 丹江口市期末)如图,在△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,连接MD,过点D作DN⊥MD,交BM于点N.CD与BM相交于点E,若点E是CD的中点,则下列结论:①AC=BE;②DM=DN;③∠AMD=45°;④NE=3ME.其中正确的有( )个.
A.4 B.3 C.2 D.1
【解答】证:∵CD⊥AB,BM⊥AC,
∴∠BDE=∠CME=90°,
∵∠DEB=∠MEC,
∴∠DBE=∠DCA,
∵∠ABC=45°,CD⊥AB,
∴△BDC是等腰直角三角形,
∴BD=CD,
∵∠BDE=∠CDA,∠DBE=∠DCA,
∴△BDE≌△CDA(ASA),
∴BE=AC,
∵∠BDC=∠NDM=90°,
∴∠BDN=∠CDM,
∵∠DBN=∠DCM,BD=CD,
∴△BDN≌△CDM(ASA),
∴DM=DN,
∵∠NDM=90°,
∴△DNM是等腰直角三角形,
∴∠DMN=45°,
∴∠AMD=45°,
故①②③正确,
过点D作DF⊥MN于点F,则∠DFE=∠CME=90°,
∵DN⊥MD,DN=DM,
∴MN=2FM=2FN,
∵点E是CD的中点,
∴DE=CE,
∵∠DEF=∠CEM,∠DFE=∠CME,
∴△DEF≌△CEM(AAS),
∴ME=EF,
∴MN=2MF=4ME,
∴NE=3ME,
故④正确,
本题选:A.
7.(2023秋 罗湖区校级期末)如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=3,则CE2+CF2的值为( )
A.6 B.9 C.18 D.36
【解答】解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=∠ACB,∠ACF=∠ACD,即∠ECF=(∠ACB+∠ACD)=90°,
又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,
∴CM=EM=MF=3,EF=6,
由勾股定理可知CE2+CF2=EF2=36,
故选:D.
8.(2023秋 郏县期末)如图,直线l1:y=x+2与直线l2:y=kx+b相交于点P(m,4),则方程组的解是( )
A. B. C. D.
【解答】解:将(m,4)代入y=x+2得4=m+2,
解得m=2,
∴点P坐标为(2,4),
∴方程组的解为:.
故选:D.
9.(2023秋 金东区期末)如图,是由四个全等的直角三角形拼成的“赵爽弦图”,得到正方形ABCD与正方形EFGH,连结DF.若S正方形ABCD=5,EF=BG,则DF的长为( )
A.2 B. C.3 D.
【解答】解:∵S正方形ABCD=5,四边形ABCD为正方形,
∴AD=AB=BC=CD=.
∵四边形EFGH为正方形,
∴EH=EF=FG=HG.
由题可知:△ADE≌△ABF≌△BCG≌△CDH.
∵EF=BG,
∴EF=AF,
∴E是中点,
即AE=EF,
∴.
∴△ADE≌△DEF(SAS).
即DF=AD=.
故选:B.
10.(2023秋 法库县期末)一列动车从A地开往B地,一列普通列车从B地开往A地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示y与x之间的函数关系.下列叙述错误的是( )
A.AB两地相距1000千米
B.两车出发后3小时相遇
C.动车的速度为千米/时
D.普通列车行驶t小时后,动车到达终点B地,此时普通列车还需行驶千米到达A地
【解答】解:由图可得,
AB两地相距1000千米,故选项A正确,不符合题意;
两车出发3小时相遇,故选项B正确,不符合题意;
动车的速度为:1000÷3﹣1000÷12=250千米/时,故选项C错误,符合题意;
普通列车行驶t小时后,动车到达终点B地,此时普通列车还需行驶×(12﹣)=千米到达A地,故选项D正确,不符合题意,
故选:C.
二.填空题(共8小题)
11.(2024秋 揭西县期中)平面直角坐标系中,若点P(4﹣m,3+m)在x轴上,则点P的坐标为 (7,0) ;
【解答】解:∵点P(4﹣m,3+m)在x轴上,
∴3+m=0,
解得m=﹣3,
∴4﹣m=4+3=7,
∴点P的坐标为(7,0).
故答案为:(7,0).
12.(2024秋 江阴市期中)如图,AC⊥BC,AD⊥BD,垂足分别为C、D,请你添加一个条件 BC=AD(答案不唯一) ,使得△ABD≌△BAC.
【解答】解:∵AC⊥BC,AD⊥BD,
∴∠D=∠C=90°,
而AB=BA,
∴当添加BC=AD或BD=AC时,Rt△ABD≌Rt△BAC(Hl);
当添加∠ABC=∠BAD或∠BAC=∠ABD时,△ABD≌△BAC(AAS).
故答案为:BC=AD(答案不唯一).
13.(2024秋 营口期中)如图,△ABC的边AB的垂直平分线交AC于点D,连结BD,若BD=5,AC=12,则DC= 7 .
【解答】解:∵△ABC的边AB的垂直平分线交AC于点D,连结BD,BD=5,AC=12,
∴AD=BD=5,
∴DC=AC﹣AD
=12﹣5
=7,
故答案为:7.
14.(2024秋 成都期中)如图,长方形ABCD中,AB=3,BC=1,AB在数轴上,以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为 .
【解答】解:根据题意,在长方形ABCD中,∠ABC=90°,
∵AB=3,BC=1,
∴,
∵以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,
∴,
∵A表示的数为﹣1,
∴点M所表示的数为,
故答案为:.
15.(2024秋 陆河县期中)如图:课间小林拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知DC=55cm,CE=75cm,则两张凳子的高度之和为 130 cm.
【解答】解:由题意,得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠DAC=∠ACD+∠BCE=90°,
∴∠DAC=∠BCE,
∴△ADC≌△CEB(AAS),
∴CE=AD=75cm,BE=CD=55cm,
∴两张凳子的高度之和为:AD+BE=75+55=130cm;
故答案为:130.
16.(2024秋 东莞市期中)在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=5cm,EF=6cm,则圆形容器的壁厚是 0.5 cm.
【解答】解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=5cm,
∵EF=6cm,
∴圆柱形容器的壁厚是×(6﹣5)=0.5(cm),
故答案为:0.5.
17.(2024秋 徐汇区校级期中)如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S2=225,S3=64,则AB的长为 17 .
【解答】解:在Rt△ABC中,由勾股定理得:AC2+BC2=AB2,
∴S2+S3=S1,
∵S2=225,S3=64,
∴S1=225+64=289,
即AB2=289,
∴AB==17,
故答案为:17.
18.(2024秋 南岸区期中)如图,射线①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象.目前这条线路亏损.为了扭亏,公交公司在保持票价不变的情况下,决定通过优化管理来降低运营成本.射线②是改变后y与x的函数图象.两射线与x轴的交点坐标分别是(0.5,0)、(0.3,0),则当乘客为1万人时,改变后的收支差额较之前增加 0.4 万元.
【解答】解:设①所在所在直线的解析式为y=kx+b(k≠0),则:
,
解得
∴①所在所在直线的解析式为y=2x﹣1;
由题意可知,直线②由①平移得到,
设②所在所在直线的解析式为y=mx+n,则:
,
解得,
∴所在所在直线的解析式为y=2x﹣0.6,
∴2×1﹣0.6﹣(2×1﹣1)=0.4(万元),
改变后的收支差额较之前增加0.4.
故答案为:0.4.
三.解答题(共8小题)
19.(2024秋 东港市期中)计算:
(1)
(2).
【解答】解:(1)原式=
=
=;
(2)原式=.
20.(2024秋 海淀区校级期中)已知:如图,点B,F,C,E在同一条直线上,AB∥DE,AB=DE,∠A=∠D.求证:△ABC≌△DEF.
【解答】证明:∵AB∥DE,
∴∠B=∠E,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
21.(2024秋 浙江期中)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,交AC于点D,连结EC.
(1)求∠ECB的度数;
(2)若CE=4,求BC长.
【解答】解:(1)∵DE是AC的垂直平分线,∠A=36°,
∴EC=EA,
∴∠ECD=∠A=36°.
∵AB=AC,∠A=36°,
∴,
∴∠ECB=∠ACB﹣∠ACE=72°﹣36°=36°;
(2)由(1)得∠ECD=36°.
∵AB=AC,∠A=36°,
∴.
∵∠BEC是△AEC的外角,
∴∠BEC=36°+36°=72°,
∴∠BEC=∠B,
∴BC=CE=4.
22.(2024秋 东城区校级期中)如图1,△ABC与△DBC全等,且∠ACB=∠DBC=90°,BC=6,AC=4.如图2,将△DBC沿射线BC方向平移得到△D1B1C1,连接AC1,BD1.
(1)求证:BD1=AC1且BD1∥AC1;
(2)△DBC沿射线BC方向平移的距离等于 6 时,点A与点D1之间的距离最小.
【解答】(1)证明:由图1可知,△ABC≌△DBC,
∴AC=BD,
由平移的性质可知,BD=B1D1,∠DBC=∠D1B1C1,BB1=CC1,
∴AC=B1D1,
∵∠DBC=∠ACB=90°,
∴∠D1B1C1=90°,
∴∠ACC1=∠BB1D1=90°,
在△BB1D1和△C1CA中,
,
∴△BB1D1≌C1CA(SAS),
∴∠AC1C=∠B1BD1,BD1=AC1,
∴BD1∥AC1,
∴BD1=AC1且BD1∥AC1;
(2)解:当点C于点B重合,点A与点D1之间的距离最小,
∴△DBC沿射线BC方向平移的距离等于BC=6,
故答案为:6.
23.(2024秋 拜城县期中)荡秋千一直以来都是深受小朋友们喜爱的娱乐项目,周六,丽丽与爸爸妈妈在公园里荡秋千.如图,丽丽坐在秋千的起始位置点A处,OA与地面垂直并交于点M,两脚在地面上用力一蹬,妈妈在点B处接住她后用力一推,爸爸在点C处接住她.若妈妈与爸爸到OA的水平距离BD,CE分别为1.4m和1.8m,∠BOC=90°,求DE的长.
【解答】解:依据题意可得:∠OEC=∠BDO=90°,
∴90°=∠DBO+∠BOD,
∵∠BOC=90°,
∴∠BOD+∠EOC=90°,
∴∠EOC∠DBO,
在△DBO和△EOC中,
,
∴△DBO≌△EOC(AAS),
∴OE=BD=1.4m,OD=CE=1.8m,
∴DE=OD﹣OE=1.8m﹣1.4m=0.4(m),
∴DE的长为0.4m.
24.(2024春 大同期末)消防云梯主要用于高层建筑火灾等救援任务,它能让消防员快速到达高层建筑的火灾现场,执行灭火、疏散等救援任务.如图,已知云梯最多能伸长到25m(AA′=BB′=25m),消防车高4m.某次任务中,消防车在A处将云梯伸长至最长,消防员从19m(A′M=19m)高的A′处救人后,消防车需到达B处使消防员从24m(B′M=24m)高的B′处救人,求消防车从A处向着火的楼房靠近的距离AB.
【解答】解:由题意,易得DM=4m,AD⊥B′M,A,B,D三点在同一直线上.
∴∠ADA′=90°,A′D=A′M﹣DM=19﹣4=15(m),
B′D=B′M﹣DM=24﹣4=20(m).
在Rt△AA′D中,由勾股定理,得.
在Rt△BB′D中,由勾股定理,得
∴AB=AD﹣BD=20﹣15=5(m).
答:消防车从A处向着火的楼房靠近的距离AB为5m.
25.(2023秋 庆云县期末)如图①,油纸伞是中国传统工艺品之一,起源于中国的一种纸制或布制伞.油纸伞的制作工艺十分巧妙,如图②,伞圈D沿着伞柄AP滑动时,伞柄AP始终平分同一平面内两条伞骨所成的∠BAC,伞骨BD,CD的B,C点固定不动,且到点A的距离AB=AC.
(1)当D点在伞柄AP上滑动时,处于同一平面的两条伞骨BD和CD相等吗?请说明理由.
(2)如图③,当油纸伞撑开时,伞的边缘M,N与点D在同一直线上,若∠BAC=140°,∠MBD=120°,求∠CDA的度数.
【解答】解:(1)相等.理由如下:
∵伞柄AP始终平分同一平面内两条伞骨所成的∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∵,
∴△ABD≌△ACD(SAS).
∴BD=CD.
(2)∵∠BAC=140°,
∴.
又∵∠MBD=120°,
∴∠BDA=∠MBD﹣∠BAD=120°﹣70°=50°.
∵△ABD≌△ACD,
∴∠CDA=∠BDA=50°.
26.(2024秋 江北区校级期中)如图1,△ABC是直角三角形,∠C=90°,BC=4,AC=3,点P从点B出发,以每秒1个单位长度的速度沿着B﹣C﹣A方向运动到A点停止,设y=S△ABP,点P的运动时间为x秒.
(1)直接写出y与x之间的函数表达式,并写出对应x的取值范围.
(2)在平面直角坐标系中画出y的图象,并写出y的一条性质.
(3)结合作出的图象直接写出它与函数y=x+1相交时x的值.(保留一位小数,误差不超过0.2)
【解答】解:(1)当点P在BC上时,0<x≤4,此时,
当点P在AC上时,4<x<7,此时,
综上分析可知:;
(2)把x=4代入得:y=6,
则图象经过点(4,6),
把x=7代入y=14﹣2x得:y=0,
则图象经过点(7,0),
∴连接点(0,0)和(4,6),连接点(4,6)和(7,0),且点(0,0)和(7,0)除外,如图所示:
根据函数图象可知,当0<x≤4时,y随x的增大而增大;当4<x<7时,y随x的增大而减小;
(3)根据函数图象可知,作出的图象与函数y=x+1的交点的横坐标约为4.3,2.0,
即此时x≈4.3或x=2.0.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组卷-2024-2025学年数学八年级上册苏科版
一.选择题(共10小题)
1.(2023秋 宁乡市期末)平面直角坐标系中,点P(2,3)关于x轴对称的点的坐标是( )
A.(2,3) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
2.(2023秋 槐荫区期末)的相反数是( )
A.﹣ B.± C.﹣5 D.5
3.(2023秋 怀集县期末)下列四个数字图形,是轴对称图形的是( )
A. B. C. D.
4.(2023秋 全椒县期末)如图,点E、H、G、N共线,∠E=∠N,EF=NM,添加一个条件,不能判断△EFG≌△NMH的是( )
A.EH=NG B.∠F=∠M C.FG=MH D.FG∥HM
5.(2023秋 连山区期末)如图,△ABC≌△DEF,点A与点D是对应点,点C与点F是对应点,则∠E等于( )
A.30° B.50° C.60° D.100°
6.(2023秋 丹江口市期末)如图,在△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,连接MD,过点D作DN⊥MD,交BM于点N.CD与BM相交于点E,若点E是CD的中点,则下列结论:①AC=BE;②DM=DN;③∠AMD=45°;④NE=3ME.其中正确的有( )个.
A.4 B.3 C.2 D.1
7.(2023秋 罗湖区校级期末)如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=3,则CE2+CF2的值为( )
A.6 B.9 C.18 D.36
8.(2023秋 郏县期末)如图,直线l1:y=x+2与直线l2:y=kx+b相交于点P(m,4),则方程组的解是( )
A. B. C. D.
9.(2023秋 金东区期末)如图,是由四个全等的直角三角形拼成的“赵爽弦图”,得到正方形ABCD与正方形EFGH,连结DF.若S正方形ABCD=5,EF=BG,则DF的长为( )
A.2 B. C.3 D.
10.(2023秋 法库县期末)一列动车从A地开往B地,一列普通列车从B地开往A地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示y与x之间的函数关系.下列叙述错误的是( )
A.AB两地相距1000千米
B.两车出发后3小时相遇
C.动车的速度为千米/时
D.普通列车行驶t小时后,动车到达终点B地,此时普通列车还需行驶千米到达A地
二.填空题(共8小题)
11.(2024秋 揭西县期中)平面直角坐标系中,若点P(4﹣m,3+m)在x轴上,则点P的坐标为 ;
12.(2024秋 江阴市期中)如图,AC⊥BC,AD⊥BD,垂足分别为C、D,请你添加一个条件 ,使得△ABD≌△BAC.
13.(2024秋 营口期中)如图,△ABC的边AB的垂直平分线交AC于点D,连结BD,若BD=5,AC=12,则DC= .
14.(2024秋 成都期中)如图,长方形ABCD中,AB=3,BC=1,AB在数轴上,以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为 .
15.(2024秋 陆河县期中)如图:课间小林拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知DC=55cm,CE=75cm,则两张凳子的高度之和为 cm.
16.(2024秋 东莞市期中)在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=5cm,EF=6cm,则圆形容器的壁厚是 cm.
17.(2024秋 徐汇区校级期中)如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S2=225,S3=64,则AB的长为 .
18.(2024秋 南岸区期中)如图,射线①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象.目前这条线路亏损.为了扭亏,公交公司在保持票价不变的情况下,决定通过优化管理来降低运营成本.射线②是改变后y与x的函数图象.两射线与x轴的交点坐标分别是(0.5,0)、(0.3,0),则当乘客为1万人时,改变后的收支差额较之前增加 万元.
三.解答题(共8小题)
19.(2024秋 东港市期中)计算:
(1)
(2).
20.(2024秋 海淀区校级期中)已知:如图,点B,F,C,E在同一条直线上,AB∥DE,AB=DE,∠A=∠D.求证:△ABC≌△DEF.
21.(2024秋 浙江期中)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,交AC于点D,连结EC.
(1)求∠ECB的度数;
(2)若CE=4,求BC长.
22.(2024秋 东城区校级期中)如图1,△ABC与△DBC全等,且∠ACB=∠DBC=90°,BC=6,AC=4.如图2,将△DBC沿射线BC方向平移得到△D1B1C1,连接AC1,BD1.
(1)求证:BD1=AC1且BD1∥AC1;
(2)△DBC沿射线BC方向平移的距离等于 时,点A与点D1之间的距离最小.
23.(2024秋 拜城县期中)荡秋千一直以来都是深受小朋友们喜爱的娱乐项目,周六,丽丽与爸爸妈妈在公园里荡秋千.如图,丽丽坐在秋千的起始位置点A处,OA与地面垂直并交于点M,两脚在地面上用力一蹬,妈妈在点B处接住她后用力一推,爸爸在点C处接住她.若妈妈与爸爸到OA的水平距离BD,CE分别为1.4m和1.8m,∠BOC=90°,求DE的长.
24.(2024春 大同期末)消防云梯主要用于高层建筑火灾等救援任务,它能让消防员快速到达高层建筑的火灾现场,执行灭火、疏散等救援任务.如图,已知云梯最多能伸长到25m(AA′=BB′=25m),消防车高4m.某次任务中,消防车在A处将云梯伸长至最长,消防员从19m(A′M=19m)高的A′处救人后,消防车需到达B处使消防员从24m(B′M=24m)高的B′处救人,求消防车从A处向着火的楼房靠近的距离AB.
25.(2023秋 庆云县期末)如图①,油纸伞是中国传统工艺品之一,起源于中国的一种纸制或布制伞.油纸伞的制作工艺十分巧妙,如图②,伞圈D沿着伞柄AP滑动时,伞柄AP始终平分同一平面内两条伞骨所成的∠BAC,伞骨BD,CD的B,C点固定不动,且到点A的距离AB=AC.
(1)当D点在伞柄AP上滑动时,处于同一平面的两条伞骨BD和CD相等吗?请说明理由.
(2)如图③,当油纸伞撑开时,伞的边缘M,N与点D在同一直线上,若∠BAC=140°,∠MBD=120°,求∠CDA的度数.
26.(2024秋 江北区校级期中)如图1,△ABC是直角三角形,∠C=90°,BC=4,AC=3,点P从点B出发,以每秒1个单位长度的速度沿着B﹣C﹣A方向运动到A点停止,设y=S△ABP,点P的运动时间为x秒.
(1)直接写出y与x之间的函数表达式,并写出对应x的取值范围.
(2)在平面直角坐标系中画出y的图象,并写出y的一条性质.
(3)结合作出的图象直接写出它与函数y=x+1相交时x的值.(保留一位小数,误差不超过0.2)
期末真题重组卷-2024-2025学年数学八年级上册苏科版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 宁乡市期末)平面直角坐标系中,点P(2,3)关于x轴对称的点的坐标是( )
A.(2,3) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
【解答】解:点P(2,3)关于x轴对称的点的坐标为(2,﹣3).
故选:C.
2.(2023秋 槐荫区期末)的相反数是( )
A.﹣ B.± C.﹣5 D.5
【解答】解:的相反数是﹣,
故选:A.
3.(2023秋 怀集县期末)下列四个数字图形,是轴对称图形的是( )
A. B. C. D.
【解答】解:A、是中心对称图形,故本选项不符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、是轴对称图形,故本选项符合题意.
故选:D.
4.(2023秋 全椒县期末)如图,点E、H、G、N共线,∠E=∠N,EF=NM,添加一个条件,不能判断△EFG≌△NMH的是( )
A.EH=NG B.∠F=∠M C.FG=MH D.FG∥HM
【解答】解:在△EFG与△NMH中,已知,∠E=∠N,EF=NM,
A.由EH=NG可得EG=NH,所以添加条件EH=NG,根据SAS可证△EFG≌△NMH,故本选项不符合题意;
B.添加条件∠F=∠M,根据ASA可证△EFG≌△NMH,故本选项不符合题意;
C.添加条件FG=MH,不能证明△EFG≌△NMH,故本选项符合题意;
D.由FG∥HM可得∠EGF=∠NHM,所以添加条件FG∥HM,根据AAS可证△EFG≌△NMH,故本选项不符合题意;
故选:C.
5.(2023秋 连山区期末)如图,△ABC≌△DEF,点A与点D是对应点,点C与点F是对应点,则∠E等于( )
A.30° B.50° C.60° D.100°
【解答】解:∵△ABC≌△DEF,
∴∠D=∠A=50°,
∴∠E=180°﹣∠D﹣∠F=30°,
故选:A.
6.(2023秋 丹江口市期末)如图,在△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,连接MD,过点D作DN⊥MD,交BM于点N.CD与BM相交于点E,若点E是CD的中点,则下列结论:①AC=BE;②DM=DN;③∠AMD=45°;④NE=3ME.其中正确的有( )个.
A.4 B.3 C.2 D.1
【解答】证:∵CD⊥AB,BM⊥AC,
∴∠BDE=∠CME=90°,
∵∠DEB=∠MEC,
∴∠DBE=∠DCA,
∵∠ABC=45°,CD⊥AB,
∴△BDC是等腰直角三角形,
∴BD=CD,
∵∠BDE=∠CDA,∠DBE=∠DCA,
∴△BDE≌△CDA(ASA),
∴BE=AC,
∵∠BDC=∠NDM=90°,
∴∠BDN=∠CDM,
∵∠DBN=∠DCM,BD=CD,
∴△BDN≌△CDM(ASA),
∴DM=DN,
∵∠NDM=90°,
∴△DNM是等腰直角三角形,
∴∠DMN=45°,
∴∠AMD=45°,
故①②③正确,
过点D作DF⊥MN于点F,则∠DFE=∠CME=90°,
∵DN⊥MD,DN=DM,
∴MN=2FM=2FN,
∵点E是CD的中点,
∴DE=CE,
∵∠DEF=∠CEM,∠DFE=∠CME,
∴△DEF≌△CEM(AAS),
∴ME=EF,
∴MN=2MF=4ME,
∴NE=3ME,
故④正确,
本题选:A.
7.(2023秋 罗湖区校级期末)如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=3,则CE2+CF2的值为( )
A.6 B.9 C.18 D.36
【解答】解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=∠ACB,∠ACF=∠ACD,即∠ECF=(∠ACB+∠ACD)=90°,
又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,
∴CM=EM=MF=3,EF=6,
由勾股定理可知CE2+CF2=EF2=36,
故选:D.
8.(2023秋 郏县期末)如图,直线l1:y=x+2与直线l2:y=kx+b相交于点P(m,4),则方程组的解是( )
A. B. C. D.
【解答】解:将(m,4)代入y=x+2得4=m+2,
解得m=2,
∴点P坐标为(2,4),
∴方程组的解为:.
故选:D.
9.(2023秋 金东区期末)如图,是由四个全等的直角三角形拼成的“赵爽弦图”,得到正方形ABCD与正方形EFGH,连结DF.若S正方形ABCD=5,EF=BG,则DF的长为( )
A.2 B. C.3 D.
【解答】解:∵S正方形ABCD=5,四边形ABCD为正方形,
∴AD=AB=BC=CD=.
∵四边形EFGH为正方形,
∴EH=EF=FG=HG.
由题可知:△ADE≌△ABF≌△BCG≌△CDH.
∵EF=BG,
∴EF=AF,
∴E是中点,
即AE=EF,
∴.
∴△ADE≌△DEF(SAS).
即DF=AD=.
故选:B.
10.(2023秋 法库县期末)一列动车从A地开往B地,一列普通列车从B地开往A地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示y与x之间的函数关系.下列叙述错误的是( )
A.AB两地相距1000千米
B.两车出发后3小时相遇
C.动车的速度为千米/时
D.普通列车行驶t小时后,动车到达终点B地,此时普通列车还需行驶千米到达A地
【解答】解:由图可得,
AB两地相距1000千米,故选项A正确,不符合题意;
两车出发3小时相遇,故选项B正确,不符合题意;
动车的速度为:1000÷3﹣1000÷12=250千米/时,故选项C错误,符合题意;
普通列车行驶t小时后,动车到达终点B地,此时普通列车还需行驶×(12﹣)=千米到达A地,故选项D正确,不符合题意,
故选:C.
二.填空题(共8小题)
11.(2024秋 揭西县期中)平面直角坐标系中,若点P(4﹣m,3+m)在x轴上,则点P的坐标为 (7,0) ;
【解答】解:∵点P(4﹣m,3+m)在x轴上,
∴3+m=0,
解得m=﹣3,
∴4﹣m=4+3=7,
∴点P的坐标为(7,0).
故答案为:(7,0).
12.(2024秋 江阴市期中)如图,AC⊥BC,AD⊥BD,垂足分别为C、D,请你添加一个条件 BC=AD(答案不唯一) ,使得△ABD≌△BAC.
【解答】解:∵AC⊥BC,AD⊥BD,
∴∠D=∠C=90°,
而AB=BA,
∴当添加BC=AD或BD=AC时,Rt△ABD≌Rt△BAC(Hl);
当添加∠ABC=∠BAD或∠BAC=∠ABD时,△ABD≌△BAC(AAS).
故答案为:BC=AD(答案不唯一).
13.(2024秋 营口期中)如图,△ABC的边AB的垂直平分线交AC于点D,连结BD,若BD=5,AC=12,则DC= 7 .
【解答】解:∵△ABC的边AB的垂直平分线交AC于点D,连结BD,BD=5,AC=12,
∴AD=BD=5,
∴DC=AC﹣AD
=12﹣5
=7,
故答案为:7.
14.(2024秋 成都期中)如图,长方形ABCD中,AB=3,BC=1,AB在数轴上,以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为 .
【解答】解:根据题意,在长方形ABCD中,∠ABC=90°,
∵AB=3,BC=1,
∴,
∵以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,
∴,
∵A表示的数为﹣1,
∴点M所表示的数为,
故答案为:.
15.(2024秋 陆河县期中)如图:课间小林拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知DC=55cm,CE=75cm,则两张凳子的高度之和为 130 cm.
【解答】解:由题意,得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠DAC=∠ACD+∠BCE=90°,
∴∠DAC=∠BCE,
∴△ADC≌△CEB(AAS),
∴CE=AD=75cm,BE=CD=55cm,
∴两张凳子的高度之和为:AD+BE=75+55=130cm;
故答案为:130.
16.(2024秋 东莞市期中)在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=5cm,EF=6cm,则圆形容器的壁厚是 0.5 cm.
【解答】解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=5cm,
∵EF=6cm,
∴圆柱形容器的壁厚是×(6﹣5)=0.5(cm),
故答案为:0.5.
17.(2024秋 徐汇区校级期中)如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S2=225,S3=64,则AB的长为 17 .
【解答】解:在Rt△ABC中,由勾股定理得:AC2+BC2=AB2,
∴S2+S3=S1,
∵S2=225,S3=64,
∴S1=225+64=289,
即AB2=289,
∴AB==17,
故答案为:17.
18.(2024秋 南岸区期中)如图,射线①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象.目前这条线路亏损.为了扭亏,公交公司在保持票价不变的情况下,决定通过优化管理来降低运营成本.射线②是改变后y与x的函数图象.两射线与x轴的交点坐标分别是(0.5,0)、(0.3,0),则当乘客为1万人时,改变后的收支差额较之前增加 0.4 万元.
【解答】解:设①所在所在直线的解析式为y=kx+b(k≠0),则:
,
解得
∴①所在所在直线的解析式为y=2x﹣1;
由题意可知,直线②由①平移得到,
设②所在所在直线的解析式为y=mx+n,则:
,
解得,
∴所在所在直线的解析式为y=2x﹣0.6,
∴2×1﹣0.6﹣(2×1﹣1)=0.4(万元),
改变后的收支差额较之前增加0.4.
故答案为:0.4.
三.解答题(共8小题)
19.(2024秋 东港市期中)计算:
(1)
(2).
【解答】解:(1)原式=
=
=;
(2)原式=.
20.(2024秋 海淀区校级期中)已知:如图,点B,F,C,E在同一条直线上,AB∥DE,AB=DE,∠A=∠D.求证:△ABC≌△DEF.
【解答】证明:∵AB∥DE,
∴∠B=∠E,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
21.(2024秋 浙江期中)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,交AC于点D,连结EC.
(1)求∠ECB的度数;
(2)若CE=4,求BC长.
【解答】解:(1)∵DE是AC的垂直平分线,∠A=36°,
∴EC=EA,
∴∠ECD=∠A=36°.
∵AB=AC,∠A=36°,
∴,
∴∠ECB=∠ACB﹣∠ACE=72°﹣36°=36°;
(2)由(1)得∠ECD=36°.
∵AB=AC,∠A=36°,
∴.
∵∠BEC是△AEC的外角,
∴∠BEC=36°+36°=72°,
∴∠BEC=∠B,
∴BC=CE=4.
22.(2024秋 东城区校级期中)如图1,△ABC与△DBC全等,且∠ACB=∠DBC=90°,BC=6,AC=4.如图2,将△DBC沿射线BC方向平移得到△D1B1C1,连接AC1,BD1.
(1)求证:BD1=AC1且BD1∥AC1;
(2)△DBC沿射线BC方向平移的距离等于 6 时,点A与点D1之间的距离最小.
【解答】(1)证明:由图1可知,△ABC≌△DBC,
∴AC=BD,
由平移的性质可知,BD=B1D1,∠DBC=∠D1B1C1,BB1=CC1,
∴AC=B1D1,
∵∠DBC=∠ACB=90°,
∴∠D1B1C1=90°,
∴∠ACC1=∠BB1D1=90°,
在△BB1D1和△C1CA中,
,
∴△BB1D1≌C1CA(SAS),
∴∠AC1C=∠B1BD1,BD1=AC1,
∴BD1∥AC1,
∴BD1=AC1且BD1∥AC1;
(2)解:当点C于点B重合,点A与点D1之间的距离最小,
∴△DBC沿射线BC方向平移的距离等于BC=6,
故答案为:6.
23.(2024秋 拜城县期中)荡秋千一直以来都是深受小朋友们喜爱的娱乐项目,周六,丽丽与爸爸妈妈在公园里荡秋千.如图,丽丽坐在秋千的起始位置点A处,OA与地面垂直并交于点M,两脚在地面上用力一蹬,妈妈在点B处接住她后用力一推,爸爸在点C处接住她.若妈妈与爸爸到OA的水平距离BD,CE分别为1.4m和1.8m,∠BOC=90°,求DE的长.
【解答】解:依据题意可得:∠OEC=∠BDO=90°,
∴90°=∠DBO+∠BOD,
∵∠BOC=90°,
∴∠BOD+∠EOC=90°,
∴∠EOC∠DBO,
在△DBO和△EOC中,
,
∴△DBO≌△EOC(AAS),
∴OE=BD=1.4m,OD=CE=1.8m,
∴DE=OD﹣OE=1.8m﹣1.4m=0.4(m),
∴DE的长为0.4m.
24.(2024春 大同期末)消防云梯主要用于高层建筑火灾等救援任务,它能让消防员快速到达高层建筑的火灾现场,执行灭火、疏散等救援任务.如图,已知云梯最多能伸长到25m(AA′=BB′=25m),消防车高4m.某次任务中,消防车在A处将云梯伸长至最长,消防员从19m(A′M=19m)高的A′处救人后,消防车需到达B处使消防员从24m(B′M=24m)高的B′处救人,求消防车从A处向着火的楼房靠近的距离AB.
【解答】解:由题意,易得DM=4m,AD⊥B′M,A,B,D三点在同一直线上.
∴∠ADA′=90°,A′D=A′M﹣DM=19﹣4=15(m),
B′D=B′M﹣DM=24﹣4=20(m).
在Rt△AA′D中,由勾股定理,得.
在Rt△BB′D中,由勾股定理,得
∴AB=AD﹣BD=20﹣15=5(m).
答:消防车从A处向着火的楼房靠近的距离AB为5m.
25.(2023秋 庆云县期末)如图①,油纸伞是中国传统工艺品之一,起源于中国的一种纸制或布制伞.油纸伞的制作工艺十分巧妙,如图②,伞圈D沿着伞柄AP滑动时,伞柄AP始终平分同一平面内两条伞骨所成的∠BAC,伞骨BD,CD的B,C点固定不动,且到点A的距离AB=AC.
(1)当D点在伞柄AP上滑动时,处于同一平面的两条伞骨BD和CD相等吗?请说明理由.
(2)如图③,当油纸伞撑开时,伞的边缘M,N与点D在同一直线上,若∠BAC=140°,∠MBD=120°,求∠CDA的度数.
【解答】解:(1)相等.理由如下:
∵伞柄AP始终平分同一平面内两条伞骨所成的∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∵,
∴△ABD≌△ACD(SAS).
∴BD=CD.
(2)∵∠BAC=140°,
∴.
又∵∠MBD=120°,
∴∠BDA=∠MBD﹣∠BAD=120°﹣70°=50°.
∵△ABD≌△ACD,
∴∠CDA=∠BDA=50°.
26.(2024秋 江北区校级期中)如图1,△ABC是直角三角形,∠C=90°,BC=4,AC=3,点P从点B出发,以每秒1个单位长度的速度沿着B﹣C﹣A方向运动到A点停止,设y=S△ABP,点P的运动时间为x秒.
(1)直接写出y与x之间的函数表达式,并写出对应x的取值范围.
(2)在平面直角坐标系中画出y的图象,并写出y的一条性质.
(3)结合作出的图象直接写出它与函数y=x+1相交时x的值.(保留一位小数,误差不超过0.2)
【解答】解:(1)当点P在BC上时,0<x≤4,此时,
当点P在AC上时,4<x<7,此时,
综上分析可知:;
(2)把x=4代入得:y=6,
则图象经过点(4,6),
把x=7代入y=14﹣2x得:y=0,
则图象经过点(7,0),
∴连接点(0,0)和(4,6),连接点(4,6)和(7,0),且点(0,0)和(7,0)除外,如图所示:
根据函数图象可知,当0<x≤4时,y随x的增大而增大;当4<x<7时,y随x的增大而减小;
(3)根据函数图象可知,作出的图象与函数y=x+1的交点的横坐标约为4.3,2.0,
即此时x≈4.3或x=2.0.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
