期末真题重组卷-2024-2025学年数学九年级上册苏科版(含解析)
文档属性
| 名称 | 期末真题重组卷-2024-2025学年数学九年级上册苏科版(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末真题重组卷-2024-2025学年数学九年级上册苏科版
一.选择题(共10小题)
1.(2023秋 泉州期末)如图,在一个不透明的纸箱中,装有4张标有数字的卡片,卡片除所标数字不同外无其他差别,现从中任取一张卡片,将其数字记为k,则使一元二次方程kx2=3x+1有实数根的概率是( )
A. B.1 C. D.
2.(2023秋 南京期末)若一组数据1、3、5、7、x的方差比另一组数据11、13、15、17、19的方差小,则x不可以是( )
A.10 B.8 C.6 D.4
3.(2023秋 船山区期末)若关于x的方程(3﹣a)x2﹣x=0是一元二次方程,则a的取值范围( )
A.a≠0 B.a≠3 C.a<3 D.a>3
4.(2021秋 义乌市期末)为调查某班学生每天使用零花钱的情况,小明随机调查了30名同学,结果如表:
每天使用零花钱(单位:元) 5 10 15 20 25
人数 2 5 8 9 6
则这30名同学每天使用的零花钱的众数和中位数分别是( )
A.20,15 B.20,17.5 C.20,20 D.15,15
5.(2023秋 华安县校级期末)用配方法解一元二次方程x2﹣4x+1=0,下列变形正确的是( )
A.(x﹣2)2﹣3=0 B.(x+4)2=15
C.(x+2)2=3 D.(x﹣2)2=﹣3
6.(2023秋 滁州期末)高速公路的隧道和桥梁最多,如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=8米,净高CD=8米,则此圆的半径OA=( )
A.5米 B.米 C.6米 D.米
7.(2023秋 大兴区期末)如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为2,则BD的长为( )
A.2 B.2 C.2 D.4
8.(2023秋 富锦市校级期末)某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,共有多少个球队参加比赛?设有x个球队参加比赛,则可列方程为( )
A.x(x+1)=36 B.x(x﹣1)=36
C. D.
9.(2023秋 大兴区期末)如图,点A,B在⊙O上,且点A,O,B不在同一条直线上,点P是⊙O上一个动点(点P不与点A,B重合),在点P运动的过程中,有如下四个结论:
①恰好存在一点P,使得∠PAB=90°;
②若直线OP垂直于AB,则∠OAP=∠OBP;
③∠APB的大小始终不变.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
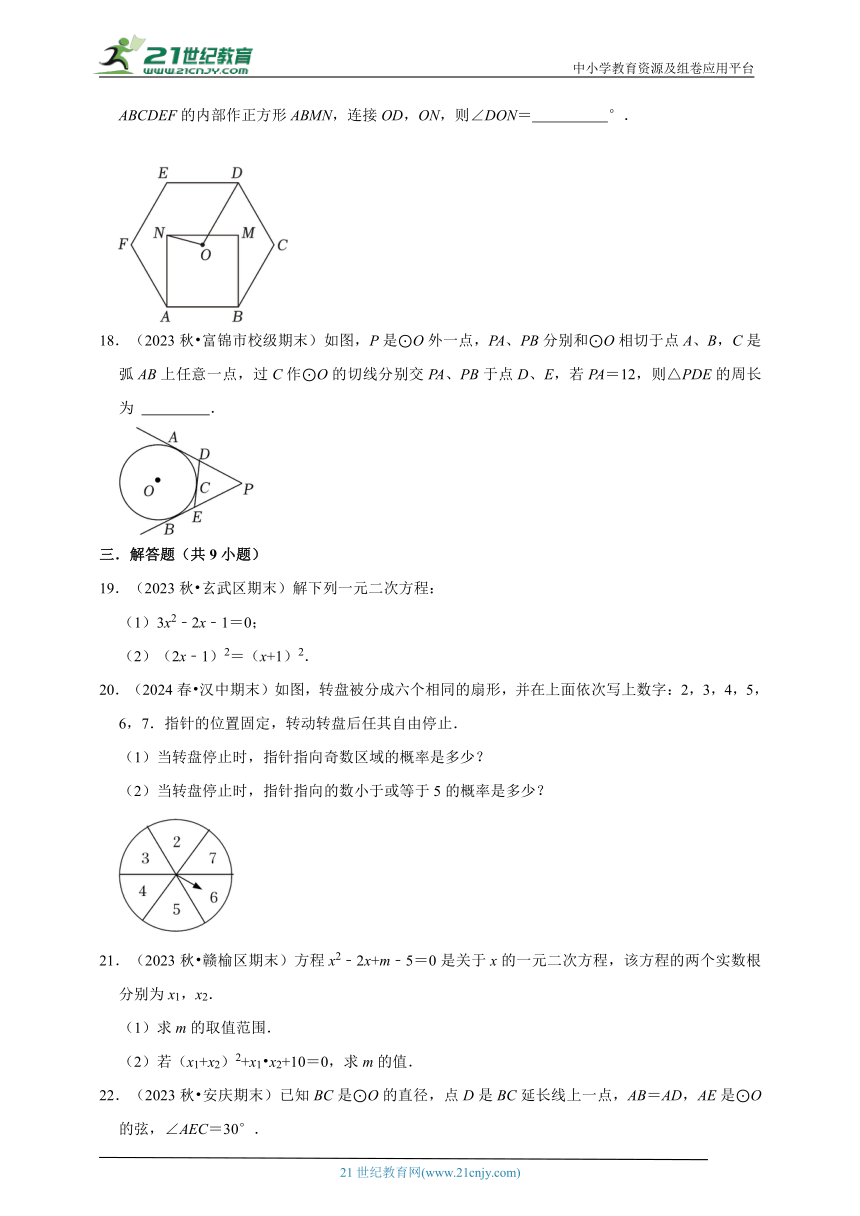
10.(2023秋 潍城区期末)中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A,B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.8千米,则这段圆曲线的长为( )
A. B. C. D.
二.填空题(共8小题)
11.(2023秋 青龙县期末)若一组数据3,4,x,6,7的众数是3,则这组数据的中位数为 .
12.(2023秋 新吴区期末)甲、乙、丙三名运动员在5次射击训练中,平均成绩都是8.5环,方差分别是S甲2=0.7,S乙2=0.2,S丙2=1.2,则这三名运动员中5次训练成绩最稳定的是 (填“甲”或“乙”或“丙”).
13.(2023秋 建邺区期末)如图,一块飞镖游戏板由除颜色外都相同的9个小正方形构成.假设飞镖击中每1块小正方形是等可能的(击中小正方形的边界或没有击中游戏板,则重投一次).任意投掷飞镖一次,击中黑色区域的概率是 .
14.(2023秋 彰武县期末)若关于x的一元二次方程x2﹣3x+2=0的一个实数根是a,则4a2﹣12a﹣3的值为 .
15.(2022秋 双牌县期末)等腰三角形的边长是方程x2﹣6x+8=0的解,则这个三角形的周长是 .
16.(2023秋 道县期末)如图所示,在宽为20米、长为32米的矩形地面上,修筑同样宽的道路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540平方米,则道路的宽为 米.
17.(2023秋 楚雄市校级期末)如图,点O是正六边形ABCDEF的中心,以AB为边在正六边形ABCDEF的内部作正方形ABMN,连接OD,ON,则∠DON= °.
18.(2023秋 富锦市校级期末)如图,P是⊙O外一点,PA、PB分别和⊙O相切于点A、B,C是弧AB上任意一点,过C作⊙O的切线分别交PA、PB于点D、E,若PA=12,则△PDE的周长为 .
三.解答题(共9小题)
19.(2023秋 玄武区期末)解下列一元二次方程:
(1)3x2﹣2x﹣1=0;
(2)(2x﹣1)2=(x+1)2.
20.(2024春 汉中期末)如图,转盘被分成六个相同的扇形,并在上面依次写上数字:2,3,4,5,6,7.指针的位置固定,转动转盘后任其自由停止.
(1)当转盘停止时,指针指向奇数区域的概率是多少?
(2)当转盘停止时,指针指向的数小于或等于5的概率是多少?
21.(2023秋 赣榆区期末)方程x2﹣2x+m﹣5=0是关于x的一元二次方程,该方程的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若(x1+x2)2+x1 x2+10=0,求m的值.
22.(2023秋 安庆期末)已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为10,求AE的长.
23.(2023秋 盘州市期末)配方法不仅可以解一元二次方程,还可以求最值.
例如:求代数式2x2+4x+5的最值.
解:2x2+4x+5
=(2x2+4x)+5(分离常数项)
=2(x2+2x)+5(提二次项系数)
(配方)
∵2(x+1)2≥0
∴2(x+1)2+3≥3
∴当x=﹣1时,代数式2x2+4x+5取得最小值是3
运用以上方法,解答下列问题:
(1)求代数式﹣a2+6a﹣4的最值;
(2)关于x的方程mx2﹣3(m+2)x+2m+7=0(m≠0).求证:无论m取何值,方程总有两个不相等的实数根.
24.(2023秋 上城区期末)如图,正六边形ABCDEF内接于⊙O,连接AD、CE交于点G,DG=2.
(1)求正六边形ABCDEF的边长;
(2)求阴影部分的面积.
25.(2023秋 东坡区期末)某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
26.(2023秋 苏州期末)大数据监测显示,我国中学生的总体近视率达71.1%.为了了解学生的视力健康情况,某校从八、九年级各随机抽取20名学生进行视力检查,并对其视力情况的数据进行整理和分析.视力情况共分4组:A.视力≥5.0,视力正常;B.视力=4.9,轻度视力不良;C.4.6≤视力≤4.8,中度视力不良;D.视力≤4.5,重度视力不良.下面给出了部分信息:
抽取的八年级学生的视力在C组的数据是:4.6,4.6,4.7,4.7,4.8,4.8;
抽取的九年级学生的视力在C组的数据是:4.6,4.7,4.8,4.7,4.7,4.8,4.7,4.7;
被抽取的八、九年级学生视力的平均数、中位数、众数如下表:
平均数 中位数 众数
八年级 4.82 a 4.9
九年级 4.82 4.8 4.7
(1)填空:a= ,m= ;
(2)根据以上数据分析,你认为该校八年级和九年级学生的视力情况谁更健康,请说明理由(写出一条理由即可);
(3)该校八年级共有学生500人,请估计八年级学生视力正常的人数.
27.(2023秋 南开区期末)在△ABC中,∠C=90°,以边AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为的中点,⊙O的半径为2,求AB的长.
期末真题重组卷-2024-2025学年数学九年级上册苏科版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 泉州期末)如图,在一个不透明的纸箱中,装有4张标有数字的卡片,卡片除所标数字不同外无其他差别,现从中任取一张卡片,将其数字记为k,则使一元二次方程kx2=3x+1有实数根的概率是( )
A. B.1 C. D.
【解答】解:一元二次方程kx2=3x+1化为一般式为kx2﹣3x﹣1=0,
∵方程有实数根,
∴k≠0且Δ=(﹣3)2﹣4k×(﹣1)≥0,
解得k≥﹣且k≠0,
∴任取一张卡片,将其数字记为k,则使一元二次方程kx2=3x+1有实数根的概率==.
故选:D.
2.(2023秋 南京期末)若一组数据1、3、5、7、x的方差比另一组数据11、13、15、17、19的方差小,则x不可以是( )
A.10 B.8 C.6 D.4
【解答】解:数据11、13、15、17、19中,相邻两个数相差为2,一组数据1,3,5,7,x前4个数据也是相差2,
若x=9或x=﹣1时,两组数据方差相等,
数据1、3、5、7、x的方差比另一组数据11、13、15、17、19的方差小,
则x的值不可能是10.
故选:A.
3.(2023秋 船山区期末)若关于x的方程(3﹣a)x2﹣x=0是一元二次方程,则a的取值范围( )
A.a≠0 B.a≠3 C.a<3 D.a>3
【解答】解:∵关于x的方程(3﹣a)x2﹣x=0是一元二次方程,
∴3﹣a≠0,
解得a≠3.
故选:B.
4.(2021秋 义乌市期末)为调查某班学生每天使用零花钱的情况,小明随机调查了30名同学,结果如表:
每天使用零花钱(单位:元) 5 10 15 20 25
人数 2 5 8 9 6
则这30名同学每天使用的零花钱的众数和中位数分别是( )
A.20,15 B.20,17.5 C.20,20 D.15,15
【解答】解:20出现了9次,出现的次数最多,所以这30名同学每天使用的零花钱的众数为20元;
30个数据中,第15个和第16个数分别为15、20,它们的平均数为17.5,所以这30名同学每天使用的零花钱的中位数为17.5元.
故选:B.
5.(2023秋 华安县校级期末)用配方法解一元二次方程x2﹣4x+1=0,下列变形正确的是( )
A.(x﹣2)2﹣3=0 B.(x+4)2=15
C.(x+2)2=3 D.(x﹣2)2=﹣3
【解答】解:x2﹣4x+1=0,
x2﹣4x=﹣1,
x2﹣4x+4=﹣1+4,
(x﹣2)2﹣3=0,
故选:A.
6.(2023秋 滁州期末)高速公路的隧道和桥梁最多,如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=8米,净高CD=8米,则此圆的半径OA=( )
A.5米 B.米 C.6米 D.米
【解答】解:设⊙O的半径是r米,
∵CD⊥AB,
∴AD=AB=4(米),
∵OA2=OD2+AD2,
∴r2=(8﹣r)2+42,
∴r=5,
∴⊙O的半径OA是5米.
故选:A.
7.(2023秋 大兴区期末)如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为2,则BD的长为( )
A.2 B.2 C.2 D.4
【解答】解:如图:连接OB,
∵BD是⊙O的切线,
∴∠OBD=90°,
∵四边形OABC为菱形,
∴OA=AB,
∵OA=OB,
∴OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠ODB=30°,
∴OD=2OB=4,
由勾股定理得,BD==2,
故选:C.
8.(2023秋 富锦市校级期末)某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,共有多少个球队参加比赛?设有x个球队参加比赛,则可列方程为( )
A.x(x+1)=36 B.x(x﹣1)=36
C. D.
【解答】解:设有x个球队参加比赛,根据题意得:
.
故选:D.
9.(2023秋 大兴区期末)如图,点A,B在⊙O上,且点A,O,B不在同一条直线上,点P是⊙O上一个动点(点P不与点A,B重合),在点P运动的过程中,有如下四个结论:
①恰好存在一点P,使得∠PAB=90°;
②若直线OP垂直于AB,则∠OAP=∠OBP;
③∠APB的大小始终不变.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
【解答】解:①当点B,O,P三点在同一条直线上时,BP为⊙O的直径,
∴∠PAB=90°,故正确,符合题意;
②∵OP垂直于AB,OA=OB,
∴∠OAP=∠OBP;故正确,符合题意;
③如图,当点P在优弧APB上时,
∠APB=∠AOB,
当点P在劣弧AB上时,
∠AP′B=180°﹣∠APB=180°﹣AOB,
∵∠APB与∠AP′B不一定相等,
∴∠APB的大小会变化,故③错误,不符合题意,
故选:A.
10.(2023秋 潍城区期末)中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A,B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.8千米,则这段圆曲线的长为( )
A. B. C. D.
【解答】解:∵CA,CB是切线,
∴OA⊥AC,OB⊥CB,
∴∠OAC=∠OBC=90°,
∴∠AOB+∠ACB=180°,
∵∠ACB+α=180°,
∴∠AOB=α=60°,
∴的长==.
故选:C.
二.填空题(共8小题)
11.(2023秋 青龙县期末)若一组数据3,4,x,6,7的众数是3,则这组数据的中位数为 4 .
【解答】解:数据3,4,x,6,7的众数是3,因此x=3,
将数据3,4,3,6,7排序后处在第3位的数是4,因此中位数是4.
故答案为:4.
12.(2023秋 新吴区期末)甲、乙、丙三名运动员在5次射击训练中,平均成绩都是8.5环,方差分别是S甲2=0.7,S乙2=0.2,S丙2=1.2,则这三名运动员中5次训练成绩最稳定的是 乙 (填“甲”或“乙”或“丙”).
【解答】解:∵S甲2=0.7,S乙2=0.2,S丙2=1.2,
∴S乙2<S甲2<S丙2,
∴这三名运动员中5次训练成绩最稳定的是乙.
故答案为:乙.
13.(2023秋 建邺区期末)如图,一块飞镖游戏板由除颜色外都相同的9个小正方形构成.假设飞镖击中每1块小正方形是等可能的(击中小正方形的边界或没有击中游戏板,则重投一次).任意投掷飞镖一次,击中黑色区域的概率是 .
【解答】解:∵共有9种小正方形,其中黑色正方形的有3个,
∴小刚任意投掷飞镖一次,刚好击中黑色区域的概率是=,
故答案为:.
14.(2023秋 彰武县期末)若关于x的一元二次方程x2﹣3x+2=0的一个实数根是a,则4a2﹣12a﹣3的值为 ﹣11 .
【解答】解:把x=a代入方程x2﹣3x+2=0得a2﹣3a+2=0,
∴a2﹣3a=﹣2,
∴4a2﹣12a﹣3
=4(a2﹣3a)﹣3
=4×(﹣2)﹣3
=﹣11.
故答案为:﹣11.
方法二:x2﹣3x+2=0,
(x﹣2)(x﹣1)=0,
∴x=2或x=1,
∴a=2或1,
∴4a2﹣12a﹣3=﹣11.
故答案为:﹣11.
15.(2022秋 双牌县期末)等腰三角形的边长是方程x2﹣6x+8=0的解,则这个三角形的周长是 10或6或12 .
【解答】解:∵x2﹣6x+8=0,
∴(x﹣2)(x﹣4)=0,
解得:x=2或x=4,
∵等腰三角形的边长是方程x2﹣6x+8=0的解,
∴当2是等腰三角形的腰时,2+2=4,不能组成三角形,舍去;
当4是等腰三角形的腰时,2+4>4,则这个三角形的周长为2+4+4=10.
当边长为2的等边三角形,得出这个三角形的周长为2+2+2=6.
当边长为4的等边三角形,得出这个三角形的周长为4+4+4=12.
∴这个三角形的周长为10或6或12.
故答案为:10或6或12.
16.(2023秋 道县期末)如图所示,在宽为20米、长为32米的矩形地面上,修筑同样宽的道路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540平方米,则道路的宽为 2 米.
【解答】解:∵道路的宽为x米,
∴种植草坪的部分可合成长为(32﹣x)米,宽为(20﹣x)米的矩形.
依题意得:(32﹣x)(20﹣x)=540,
解得:x1=2,x2=50(舍去).
故答案为:2.
17.(2023秋 楚雄市校级期末)如图,点O是正六边形ABCDEF的中心,以AB为边在正六边形ABCDEF的内部作正方形ABMN,连接OD,ON,则∠DON= 105 °.
【解答】解:连接OA,OB,OE,OF,如图,
∵点O是正六边形ABCDEF的中心,
∴OA=OB=OF=OE=OD,∠AOB=∠AOF=∠FOE=∠EOD=60°,
∴△OAB为等边三角形,∠AOF+∠FOE+∠EOD=180°,
∴D,O,A在一条直线上,∠OAB=60°,OA=AB.
∵以AB为边在正六边形ABCDEF的内部作正方形ABMN,
∴∠NAB=90°,AB=AN,
∴∠NAO=30°,OA=AN,
∴∠AON=∠ANO==75°,
∴∠NOD=180°﹣∠AON=105°.
故答案为:105.
18.(2023秋 富锦市校级期末)如图,P是⊙O外一点,PA、PB分别和⊙O相切于点A、B,C是弧AB上任意一点,过C作⊙O的切线分别交PA、PB于点D、E,若PA=12,则△PDE的周长为 24 .
【解答】解:∵PA、PB分别和⊙O相切于点A、B,且PA=12.
∴PA=PB=12,
∵过C作⊙O的切线分别交PA、PB于点D、E,
∴DC=DA,EC=EB,
∴PD+DE+PE=PD+DC+EC+PE=PD+DA+EB+PE=PA+PB=12+12=24,
∴△PDE的周长为24,
故答案为:24.
三.解答题(共9小题)
19.(2023秋 玄武区期末)解下列一元二次方程:
(1)3x2﹣2x﹣1=0;
(2)(2x﹣1)2=(x+1)2.
【解答】解:(1)3x2﹣2x﹣1=0,
(3x+1)(x﹣1)=0,
∴3x+1=0或x﹣1=0,
∴x1=﹣,x2=1;
(2)(2x﹣1)2=(x+1)2,
(2x﹣1)2﹣(x+1)2=0,
(2x﹣1+x+1)(2x﹣1﹣x﹣1)=0,
3x(x﹣2)=0,
∴3x=0或x﹣2=0,
∴x1=0,x2=2.
20.(2024春 汉中期末)如图,转盘被分成六个相同的扇形,并在上面依次写上数字:2,3,4,5,6,7.指针的位置固定,转动转盘后任其自由停止.
(1)当转盘停止时,指针指向奇数区域的概率是多少?
(2)当转盘停止时,指针指向的数小于或等于5的概率是多少?
【解答】解:(1)当转盘停止转动时,指针指向数字区域2,3,4,5,6,7的机会是均等的,故共有6种均等的结果,其中指针指向奇数区域3,5,7有3种结果,
所以指针指向奇数区域的概率是;
(2)当转盘停止转动时,指针指向数字区域2,3,4,5,6,7的机会是均等的,故共有6种均等的结果,其中指针指向的数小于或等于5区域2,3,4,5有4种结果,
所以指针指向的数小于或等于5的概率是.
21.(2023秋 赣榆区期末)方程x2﹣2x+m﹣5=0是关于x的一元二次方程,该方程的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若(x1+x2)2+x1 x2+10=0,求m的值.
【解答】解:(1)根据题意得Δ=(﹣2)2﹣4(m﹣5)≥0,
解得m≤6;
(2)根据题意得x1+x2=2,x1x2=m﹣5,
∵(x1+x2)2+x1 x2+10=0,
∴22+m﹣5+10=0,
∴m=﹣9.
22.(2023秋 安庆期末)已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为10,求AE的长.
【解答】(1)证明:如图,连接OA,
∵∠AEC=30°,
∴∠B=∠AEC=30°,∠AOC=2∠AEC=60°,
∵AB=AD,
∴∠D=∠B=30°,
∴∠OAD=180°﹣∠AOC﹣∠D=90°,
∵OA是⊙O的半径,且AD⊥OA,
∴直线AD是⊙O的切线.
(2)解:如图,∵BC是⊙O的直径,且AE⊥BC于点M,
∴AM=EM,
∵∠AMO=90°,∠AOM=60°,
∴∠OAM=30°,
∴OM=OA=×10=5,
∴AM===5,
∴AE=2AM=2×5=10.
23.(2023秋 盘州市期末)配方法不仅可以解一元二次方程,还可以求最值.
例如:求代数式2x2+4x+5的最值.
解:2x2+4x+5
=(2x2+4x)+5(分离常数项)
=2(x2+2x)+5(提二次项系数)
(配方)
∵2(x+1)2≥0
∴2(x+1)2+3≥3
∴当x=﹣1时,代数式2x2+4x+5取得最小值是3
运用以上方法,解答下列问题:
(1)求代数式﹣a2+6a﹣4的最值;
(2)关于x的方程mx2﹣3(m+2)x+2m+7=0(m≠0).求证:无论m取何值,方程总有两个不相等的实数根.
【解答】(1)解:﹣a2+6a﹣4
=﹣(a2﹣6a)﹣4
=﹣(a2﹣6a+9﹣9)﹣4
=﹣[(a﹣3)2﹣9]﹣4
=﹣(a﹣3)2+5,
∵﹣(a﹣3)2≤0,
∴﹣(a﹣3)2+5≤5,
∴当a=3时,代数式﹣a2+6a﹣4取得最大值是5;
(2)证明:∵Δ=b2﹣4ac
=[﹣3(m+2)]2﹣4m(2m+7)
=9(m2+4m+4)﹣8m2﹣28m
=9m2+36m+36﹣8m2﹣28m
=m2+8m+36
=(m+4)2+20,
∵(m+4)2≥0,
∴Δ=b2﹣4ac=(m+4)2+20≥20>0,
∴无论m取何值,方程总有两个不相等的实数根.
24.(2023秋 上城区期末)如图,正六边形ABCDEF内接于⊙O,连接AD、CE交于点G,DG=2.
(1)求正六边形ABCDEF的边长;
(2)求阴影部分的面积.
【解答】解:(1)如图,连接OC,则CG⊥OD,
∵正六边形ABCDEF内接于⊙O,
∴△COD是正三角形,
∴∠COD=60°,
∵CG⊥OD,
∴OG=DG=OD=2,
∴OC=2OG=4,
即正六边形的边长为4;
(2)在Rt△COD中,OG=2,∠COG=60°,
∴CG=OG=2,
∴S阴影部分=S扇形COD﹣S△COD
=﹣×4×2
=﹣4.
25.(2023秋 东坡区期末)某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
【解答】解:(1)设A社区居民人口有x万人,则B社区有(7.5﹣x)万人,
依题意得:7.5﹣x≤2x,
解得x≥2.5.
即A社区居民人口至少有2.5万人;
(2)依题意得:1.2(1+m%)2+1×(1+m%)×(1+2m%)=7.5×76%
设m%=a,方程可化为:
1.2(1+a)2+(1+a)(1+2a)=5.7
化简得:32a2+54a﹣35=0
解得a=0.5或a=﹣(舍)
∴m=50
答:m的值为50.
26.(2023秋 苏州期末)大数据监测显示,我国中学生的总体近视率达71.1%.为了了解学生的视力健康情况,某校从八、九年级各随机抽取20名学生进行视力检查,并对其视力情况的数据进行整理和分析.视力情况共分4组:A.视力≥5.0,视力正常;B.视力=4.9,轻度视力不良;C.4.6≤视力≤4.8,中度视力不良;D.视力≤4.5,重度视力不良.下面给出了部分信息:
抽取的八年级学生的视力在C组的数据是:4.6,4.6,4.7,4.7,4.8,4.8;
抽取的九年级学生的视力在C组的数据是:4.6,4.7,4.8,4.7,4.7,4.8,4.7,4.7;
被抽取的八、九年级学生视力的平均数、中位数、众数如下表:
平均数 中位数 众数
八年级 4.82 a 4.9
九年级 4.82 4.8 4.7
(1)填空:a= 4.9 ,m= 20 ;
(2)根据以上数据分析,你认为该校八年级和九年级学生的视力情况谁更健康,请说明理由(写出一条理由即可);
(3)该校八年级共有学生500人,请估计八年级学生视力正常的人数.
【解答】解:(1)八年级学生的视力按从小到大的顺序排序后,第10个数据和第11个数据都是4.9,
∴a==4.9,
20×25%=5,20×%15=3,C组人数为8,
∴B组人数为20﹣5﹣3﹣8=4,
∴m%=100%=20%,
∴m=20,
故答案为:4.9,20;
(2)∵八年级和九年级学生的视力的平均数相等,而八年级学生的视力的中位数和众数均高于九年级,
∴八年级学生的视力情况谁更健康;
(3)500×=150(人),
估计八年级学生视力正常的人数为150人.
27.(2023秋 南开区期末)在△ABC中,∠C=90°,以边AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为的中点,⊙O的半径为2,求AB的长.
【解答】解:(1)连接OD,
∵OA为半径的圆与BC相切于点D,
∴OD⊥BC,
∴∠ODB=90°,
∵在△ABC中,∠C=90°,
∴∠ODB=∠C,
∴OD∥AC,
∴∠CAD=∠ADO=25°,
∵OA=OD,
∴∠OAD=∠ODA=25°,
∴∠BOD=2∠OAD=50°,
∴∠B=90°﹣∠BOD=40°;
(2)连接OF,OD,
由(1)得:OD∥AC,
∴∠AFO=∠FOD,
∵OA=OF,点F为的中点,
∴∠A=∠AFO,∠AOF=∠FOD,
∴∠A=∠AFO=∠AOF=60°,
∴∠B=90°﹣∠A=30°,
∵OA=OD=2,
∴OB=2OD=4,
∴AB=OA+OB=6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组卷-2024-2025学年数学九年级上册苏科版
一.选择题(共10小题)
1.(2023秋 泉州期末)如图,在一个不透明的纸箱中,装有4张标有数字的卡片,卡片除所标数字不同外无其他差别,现从中任取一张卡片,将其数字记为k,则使一元二次方程kx2=3x+1有实数根的概率是( )
A. B.1 C. D.
2.(2023秋 南京期末)若一组数据1、3、5、7、x的方差比另一组数据11、13、15、17、19的方差小,则x不可以是( )
A.10 B.8 C.6 D.4
3.(2023秋 船山区期末)若关于x的方程(3﹣a)x2﹣x=0是一元二次方程,则a的取值范围( )
A.a≠0 B.a≠3 C.a<3 D.a>3
4.(2021秋 义乌市期末)为调查某班学生每天使用零花钱的情况,小明随机调查了30名同学,结果如表:
每天使用零花钱(单位:元) 5 10 15 20 25
人数 2 5 8 9 6
则这30名同学每天使用的零花钱的众数和中位数分别是( )
A.20,15 B.20,17.5 C.20,20 D.15,15
5.(2023秋 华安县校级期末)用配方法解一元二次方程x2﹣4x+1=0,下列变形正确的是( )
A.(x﹣2)2﹣3=0 B.(x+4)2=15
C.(x+2)2=3 D.(x﹣2)2=﹣3
6.(2023秋 滁州期末)高速公路的隧道和桥梁最多,如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=8米,净高CD=8米,则此圆的半径OA=( )
A.5米 B.米 C.6米 D.米
7.(2023秋 大兴区期末)如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为2,则BD的长为( )
A.2 B.2 C.2 D.4
8.(2023秋 富锦市校级期末)某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,共有多少个球队参加比赛?设有x个球队参加比赛,则可列方程为( )
A.x(x+1)=36 B.x(x﹣1)=36
C. D.
9.(2023秋 大兴区期末)如图,点A,B在⊙O上,且点A,O,B不在同一条直线上,点P是⊙O上一个动点(点P不与点A,B重合),在点P运动的过程中,有如下四个结论:
①恰好存在一点P,使得∠PAB=90°;
②若直线OP垂直于AB,则∠OAP=∠OBP;
③∠APB的大小始终不变.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
10.(2023秋 潍城区期末)中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A,B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.8千米,则这段圆曲线的长为( )
A. B. C. D.
二.填空题(共8小题)
11.(2023秋 青龙县期末)若一组数据3,4,x,6,7的众数是3,则这组数据的中位数为 .
12.(2023秋 新吴区期末)甲、乙、丙三名运动员在5次射击训练中,平均成绩都是8.5环,方差分别是S甲2=0.7,S乙2=0.2,S丙2=1.2,则这三名运动员中5次训练成绩最稳定的是 (填“甲”或“乙”或“丙”).
13.(2023秋 建邺区期末)如图,一块飞镖游戏板由除颜色外都相同的9个小正方形构成.假设飞镖击中每1块小正方形是等可能的(击中小正方形的边界或没有击中游戏板,则重投一次).任意投掷飞镖一次,击中黑色区域的概率是 .
14.(2023秋 彰武县期末)若关于x的一元二次方程x2﹣3x+2=0的一个实数根是a,则4a2﹣12a﹣3的值为 .
15.(2022秋 双牌县期末)等腰三角形的边长是方程x2﹣6x+8=0的解,则这个三角形的周长是 .
16.(2023秋 道县期末)如图所示,在宽为20米、长为32米的矩形地面上,修筑同样宽的道路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540平方米,则道路的宽为 米.
17.(2023秋 楚雄市校级期末)如图,点O是正六边形ABCDEF的中心,以AB为边在正六边形ABCDEF的内部作正方形ABMN,连接OD,ON,则∠DON= °.
18.(2023秋 富锦市校级期末)如图,P是⊙O外一点,PA、PB分别和⊙O相切于点A、B,C是弧AB上任意一点,过C作⊙O的切线分别交PA、PB于点D、E,若PA=12,则△PDE的周长为 .
三.解答题(共9小题)
19.(2023秋 玄武区期末)解下列一元二次方程:
(1)3x2﹣2x﹣1=0;
(2)(2x﹣1)2=(x+1)2.
20.(2024春 汉中期末)如图,转盘被分成六个相同的扇形,并在上面依次写上数字:2,3,4,5,6,7.指针的位置固定,转动转盘后任其自由停止.
(1)当转盘停止时,指针指向奇数区域的概率是多少?
(2)当转盘停止时,指针指向的数小于或等于5的概率是多少?
21.(2023秋 赣榆区期末)方程x2﹣2x+m﹣5=0是关于x的一元二次方程,该方程的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若(x1+x2)2+x1 x2+10=0,求m的值.
22.(2023秋 安庆期末)已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为10,求AE的长.
23.(2023秋 盘州市期末)配方法不仅可以解一元二次方程,还可以求最值.
例如:求代数式2x2+4x+5的最值.
解:2x2+4x+5
=(2x2+4x)+5(分离常数项)
=2(x2+2x)+5(提二次项系数)
(配方)
∵2(x+1)2≥0
∴2(x+1)2+3≥3
∴当x=﹣1时,代数式2x2+4x+5取得最小值是3
运用以上方法,解答下列问题:
(1)求代数式﹣a2+6a﹣4的最值;
(2)关于x的方程mx2﹣3(m+2)x+2m+7=0(m≠0).求证:无论m取何值,方程总有两个不相等的实数根.
24.(2023秋 上城区期末)如图,正六边形ABCDEF内接于⊙O,连接AD、CE交于点G,DG=2.
(1)求正六边形ABCDEF的边长;
(2)求阴影部分的面积.
25.(2023秋 东坡区期末)某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
26.(2023秋 苏州期末)大数据监测显示,我国中学生的总体近视率达71.1%.为了了解学生的视力健康情况,某校从八、九年级各随机抽取20名学生进行视力检查,并对其视力情况的数据进行整理和分析.视力情况共分4组:A.视力≥5.0,视力正常;B.视力=4.9,轻度视力不良;C.4.6≤视力≤4.8,中度视力不良;D.视力≤4.5,重度视力不良.下面给出了部分信息:
抽取的八年级学生的视力在C组的数据是:4.6,4.6,4.7,4.7,4.8,4.8;
抽取的九年级学生的视力在C组的数据是:4.6,4.7,4.8,4.7,4.7,4.8,4.7,4.7;
被抽取的八、九年级学生视力的平均数、中位数、众数如下表:
平均数 中位数 众数
八年级 4.82 a 4.9
九年级 4.82 4.8 4.7
(1)填空:a= ,m= ;
(2)根据以上数据分析,你认为该校八年级和九年级学生的视力情况谁更健康,请说明理由(写出一条理由即可);
(3)该校八年级共有学生500人,请估计八年级学生视力正常的人数.
27.(2023秋 南开区期末)在△ABC中,∠C=90°,以边AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为的中点,⊙O的半径为2,求AB的长.
期末真题重组卷-2024-2025学年数学九年级上册苏科版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 泉州期末)如图,在一个不透明的纸箱中,装有4张标有数字的卡片,卡片除所标数字不同外无其他差别,现从中任取一张卡片,将其数字记为k,则使一元二次方程kx2=3x+1有实数根的概率是( )
A. B.1 C. D.
【解答】解:一元二次方程kx2=3x+1化为一般式为kx2﹣3x﹣1=0,
∵方程有实数根,
∴k≠0且Δ=(﹣3)2﹣4k×(﹣1)≥0,
解得k≥﹣且k≠0,
∴任取一张卡片,将其数字记为k,则使一元二次方程kx2=3x+1有实数根的概率==.
故选:D.
2.(2023秋 南京期末)若一组数据1、3、5、7、x的方差比另一组数据11、13、15、17、19的方差小,则x不可以是( )
A.10 B.8 C.6 D.4
【解答】解:数据11、13、15、17、19中,相邻两个数相差为2,一组数据1,3,5,7,x前4个数据也是相差2,
若x=9或x=﹣1时,两组数据方差相等,
数据1、3、5、7、x的方差比另一组数据11、13、15、17、19的方差小,
则x的值不可能是10.
故选:A.
3.(2023秋 船山区期末)若关于x的方程(3﹣a)x2﹣x=0是一元二次方程,则a的取值范围( )
A.a≠0 B.a≠3 C.a<3 D.a>3
【解答】解:∵关于x的方程(3﹣a)x2﹣x=0是一元二次方程,
∴3﹣a≠0,
解得a≠3.
故选:B.
4.(2021秋 义乌市期末)为调查某班学生每天使用零花钱的情况,小明随机调查了30名同学,结果如表:
每天使用零花钱(单位:元) 5 10 15 20 25
人数 2 5 8 9 6
则这30名同学每天使用的零花钱的众数和中位数分别是( )
A.20,15 B.20,17.5 C.20,20 D.15,15
【解答】解:20出现了9次,出现的次数最多,所以这30名同学每天使用的零花钱的众数为20元;
30个数据中,第15个和第16个数分别为15、20,它们的平均数为17.5,所以这30名同学每天使用的零花钱的中位数为17.5元.
故选:B.
5.(2023秋 华安县校级期末)用配方法解一元二次方程x2﹣4x+1=0,下列变形正确的是( )
A.(x﹣2)2﹣3=0 B.(x+4)2=15
C.(x+2)2=3 D.(x﹣2)2=﹣3
【解答】解:x2﹣4x+1=0,
x2﹣4x=﹣1,
x2﹣4x+4=﹣1+4,
(x﹣2)2﹣3=0,
故选:A.
6.(2023秋 滁州期末)高速公路的隧道和桥梁最多,如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=8米,净高CD=8米,则此圆的半径OA=( )
A.5米 B.米 C.6米 D.米
【解答】解:设⊙O的半径是r米,
∵CD⊥AB,
∴AD=AB=4(米),
∵OA2=OD2+AD2,
∴r2=(8﹣r)2+42,
∴r=5,
∴⊙O的半径OA是5米.
故选:A.
7.(2023秋 大兴区期末)如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为2,则BD的长为( )
A.2 B.2 C.2 D.4
【解答】解:如图:连接OB,
∵BD是⊙O的切线,
∴∠OBD=90°,
∵四边形OABC为菱形,
∴OA=AB,
∵OA=OB,
∴OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠ODB=30°,
∴OD=2OB=4,
由勾股定理得,BD==2,
故选:C.
8.(2023秋 富锦市校级期末)某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,共有多少个球队参加比赛?设有x个球队参加比赛,则可列方程为( )
A.x(x+1)=36 B.x(x﹣1)=36
C. D.
【解答】解:设有x个球队参加比赛,根据题意得:
.
故选:D.
9.(2023秋 大兴区期末)如图,点A,B在⊙O上,且点A,O,B不在同一条直线上,点P是⊙O上一个动点(点P不与点A,B重合),在点P运动的过程中,有如下四个结论:
①恰好存在一点P,使得∠PAB=90°;
②若直线OP垂直于AB,则∠OAP=∠OBP;
③∠APB的大小始终不变.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
【解答】解:①当点B,O,P三点在同一条直线上时,BP为⊙O的直径,
∴∠PAB=90°,故正确,符合题意;
②∵OP垂直于AB,OA=OB,
∴∠OAP=∠OBP;故正确,符合题意;
③如图,当点P在优弧APB上时,
∠APB=∠AOB,
当点P在劣弧AB上时,
∠AP′B=180°﹣∠APB=180°﹣AOB,
∵∠APB与∠AP′B不一定相等,
∴∠APB的大小会变化,故③错误,不符合题意,
故选:A.
10.(2023秋 潍城区期末)中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A,B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.8千米,则这段圆曲线的长为( )
A. B. C. D.
【解答】解:∵CA,CB是切线,
∴OA⊥AC,OB⊥CB,
∴∠OAC=∠OBC=90°,
∴∠AOB+∠ACB=180°,
∵∠ACB+α=180°,
∴∠AOB=α=60°,
∴的长==.
故选:C.
二.填空题(共8小题)
11.(2023秋 青龙县期末)若一组数据3,4,x,6,7的众数是3,则这组数据的中位数为 4 .
【解答】解:数据3,4,x,6,7的众数是3,因此x=3,
将数据3,4,3,6,7排序后处在第3位的数是4,因此中位数是4.
故答案为:4.
12.(2023秋 新吴区期末)甲、乙、丙三名运动员在5次射击训练中,平均成绩都是8.5环,方差分别是S甲2=0.7,S乙2=0.2,S丙2=1.2,则这三名运动员中5次训练成绩最稳定的是 乙 (填“甲”或“乙”或“丙”).
【解答】解:∵S甲2=0.7,S乙2=0.2,S丙2=1.2,
∴S乙2<S甲2<S丙2,
∴这三名运动员中5次训练成绩最稳定的是乙.
故答案为:乙.
13.(2023秋 建邺区期末)如图,一块飞镖游戏板由除颜色外都相同的9个小正方形构成.假设飞镖击中每1块小正方形是等可能的(击中小正方形的边界或没有击中游戏板,则重投一次).任意投掷飞镖一次,击中黑色区域的概率是 .
【解答】解:∵共有9种小正方形,其中黑色正方形的有3个,
∴小刚任意投掷飞镖一次,刚好击中黑色区域的概率是=,
故答案为:.
14.(2023秋 彰武县期末)若关于x的一元二次方程x2﹣3x+2=0的一个实数根是a,则4a2﹣12a﹣3的值为 ﹣11 .
【解答】解:把x=a代入方程x2﹣3x+2=0得a2﹣3a+2=0,
∴a2﹣3a=﹣2,
∴4a2﹣12a﹣3
=4(a2﹣3a)﹣3
=4×(﹣2)﹣3
=﹣11.
故答案为:﹣11.
方法二:x2﹣3x+2=0,
(x﹣2)(x﹣1)=0,
∴x=2或x=1,
∴a=2或1,
∴4a2﹣12a﹣3=﹣11.
故答案为:﹣11.
15.(2022秋 双牌县期末)等腰三角形的边长是方程x2﹣6x+8=0的解,则这个三角形的周长是 10或6或12 .
【解答】解:∵x2﹣6x+8=0,
∴(x﹣2)(x﹣4)=0,
解得:x=2或x=4,
∵等腰三角形的边长是方程x2﹣6x+8=0的解,
∴当2是等腰三角形的腰时,2+2=4,不能组成三角形,舍去;
当4是等腰三角形的腰时,2+4>4,则这个三角形的周长为2+4+4=10.
当边长为2的等边三角形,得出这个三角形的周长为2+2+2=6.
当边长为4的等边三角形,得出这个三角形的周长为4+4+4=12.
∴这个三角形的周长为10或6或12.
故答案为:10或6或12.
16.(2023秋 道县期末)如图所示,在宽为20米、长为32米的矩形地面上,修筑同样宽的道路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540平方米,则道路的宽为 2 米.
【解答】解:∵道路的宽为x米,
∴种植草坪的部分可合成长为(32﹣x)米,宽为(20﹣x)米的矩形.
依题意得:(32﹣x)(20﹣x)=540,
解得:x1=2,x2=50(舍去).
故答案为:2.
17.(2023秋 楚雄市校级期末)如图,点O是正六边形ABCDEF的中心,以AB为边在正六边形ABCDEF的内部作正方形ABMN,连接OD,ON,则∠DON= 105 °.
【解答】解:连接OA,OB,OE,OF,如图,
∵点O是正六边形ABCDEF的中心,
∴OA=OB=OF=OE=OD,∠AOB=∠AOF=∠FOE=∠EOD=60°,
∴△OAB为等边三角形,∠AOF+∠FOE+∠EOD=180°,
∴D,O,A在一条直线上,∠OAB=60°,OA=AB.
∵以AB为边在正六边形ABCDEF的内部作正方形ABMN,
∴∠NAB=90°,AB=AN,
∴∠NAO=30°,OA=AN,
∴∠AON=∠ANO==75°,
∴∠NOD=180°﹣∠AON=105°.
故答案为:105.
18.(2023秋 富锦市校级期末)如图,P是⊙O外一点,PA、PB分别和⊙O相切于点A、B,C是弧AB上任意一点,过C作⊙O的切线分别交PA、PB于点D、E,若PA=12,则△PDE的周长为 24 .
【解答】解:∵PA、PB分别和⊙O相切于点A、B,且PA=12.
∴PA=PB=12,
∵过C作⊙O的切线分别交PA、PB于点D、E,
∴DC=DA,EC=EB,
∴PD+DE+PE=PD+DC+EC+PE=PD+DA+EB+PE=PA+PB=12+12=24,
∴△PDE的周长为24,
故答案为:24.
三.解答题(共9小题)
19.(2023秋 玄武区期末)解下列一元二次方程:
(1)3x2﹣2x﹣1=0;
(2)(2x﹣1)2=(x+1)2.
【解答】解:(1)3x2﹣2x﹣1=0,
(3x+1)(x﹣1)=0,
∴3x+1=0或x﹣1=0,
∴x1=﹣,x2=1;
(2)(2x﹣1)2=(x+1)2,
(2x﹣1)2﹣(x+1)2=0,
(2x﹣1+x+1)(2x﹣1﹣x﹣1)=0,
3x(x﹣2)=0,
∴3x=0或x﹣2=0,
∴x1=0,x2=2.
20.(2024春 汉中期末)如图,转盘被分成六个相同的扇形,并在上面依次写上数字:2,3,4,5,6,7.指针的位置固定,转动转盘后任其自由停止.
(1)当转盘停止时,指针指向奇数区域的概率是多少?
(2)当转盘停止时,指针指向的数小于或等于5的概率是多少?
【解答】解:(1)当转盘停止转动时,指针指向数字区域2,3,4,5,6,7的机会是均等的,故共有6种均等的结果,其中指针指向奇数区域3,5,7有3种结果,
所以指针指向奇数区域的概率是;
(2)当转盘停止转动时,指针指向数字区域2,3,4,5,6,7的机会是均等的,故共有6种均等的结果,其中指针指向的数小于或等于5区域2,3,4,5有4种结果,
所以指针指向的数小于或等于5的概率是.
21.(2023秋 赣榆区期末)方程x2﹣2x+m﹣5=0是关于x的一元二次方程,该方程的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若(x1+x2)2+x1 x2+10=0,求m的值.
【解答】解:(1)根据题意得Δ=(﹣2)2﹣4(m﹣5)≥0,
解得m≤6;
(2)根据题意得x1+x2=2,x1x2=m﹣5,
∵(x1+x2)2+x1 x2+10=0,
∴22+m﹣5+10=0,
∴m=﹣9.
22.(2023秋 安庆期末)已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为10,求AE的长.
【解答】(1)证明:如图,连接OA,
∵∠AEC=30°,
∴∠B=∠AEC=30°,∠AOC=2∠AEC=60°,
∵AB=AD,
∴∠D=∠B=30°,
∴∠OAD=180°﹣∠AOC﹣∠D=90°,
∵OA是⊙O的半径,且AD⊥OA,
∴直线AD是⊙O的切线.
(2)解:如图,∵BC是⊙O的直径,且AE⊥BC于点M,
∴AM=EM,
∵∠AMO=90°,∠AOM=60°,
∴∠OAM=30°,
∴OM=OA=×10=5,
∴AM===5,
∴AE=2AM=2×5=10.
23.(2023秋 盘州市期末)配方法不仅可以解一元二次方程,还可以求最值.
例如:求代数式2x2+4x+5的最值.
解:2x2+4x+5
=(2x2+4x)+5(分离常数项)
=2(x2+2x)+5(提二次项系数)
(配方)
∵2(x+1)2≥0
∴2(x+1)2+3≥3
∴当x=﹣1时,代数式2x2+4x+5取得最小值是3
运用以上方法,解答下列问题:
(1)求代数式﹣a2+6a﹣4的最值;
(2)关于x的方程mx2﹣3(m+2)x+2m+7=0(m≠0).求证:无论m取何值,方程总有两个不相等的实数根.
【解答】(1)解:﹣a2+6a﹣4
=﹣(a2﹣6a)﹣4
=﹣(a2﹣6a+9﹣9)﹣4
=﹣[(a﹣3)2﹣9]﹣4
=﹣(a﹣3)2+5,
∵﹣(a﹣3)2≤0,
∴﹣(a﹣3)2+5≤5,
∴当a=3时,代数式﹣a2+6a﹣4取得最大值是5;
(2)证明:∵Δ=b2﹣4ac
=[﹣3(m+2)]2﹣4m(2m+7)
=9(m2+4m+4)﹣8m2﹣28m
=9m2+36m+36﹣8m2﹣28m
=m2+8m+36
=(m+4)2+20,
∵(m+4)2≥0,
∴Δ=b2﹣4ac=(m+4)2+20≥20>0,
∴无论m取何值,方程总有两个不相等的实数根.
24.(2023秋 上城区期末)如图,正六边形ABCDEF内接于⊙O,连接AD、CE交于点G,DG=2.
(1)求正六边形ABCDEF的边长;
(2)求阴影部分的面积.
【解答】解:(1)如图,连接OC,则CG⊥OD,
∵正六边形ABCDEF内接于⊙O,
∴△COD是正三角形,
∴∠COD=60°,
∵CG⊥OD,
∴OG=DG=OD=2,
∴OC=2OG=4,
即正六边形的边长为4;
(2)在Rt△COD中,OG=2,∠COG=60°,
∴CG=OG=2,
∴S阴影部分=S扇形COD﹣S△COD
=﹣×4×2
=﹣4.
25.(2023秋 东坡区期末)某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
【解答】解:(1)设A社区居民人口有x万人,则B社区有(7.5﹣x)万人,
依题意得:7.5﹣x≤2x,
解得x≥2.5.
即A社区居民人口至少有2.5万人;
(2)依题意得:1.2(1+m%)2+1×(1+m%)×(1+2m%)=7.5×76%
设m%=a,方程可化为:
1.2(1+a)2+(1+a)(1+2a)=5.7
化简得:32a2+54a﹣35=0
解得a=0.5或a=﹣(舍)
∴m=50
答:m的值为50.
26.(2023秋 苏州期末)大数据监测显示,我国中学生的总体近视率达71.1%.为了了解学生的视力健康情况,某校从八、九年级各随机抽取20名学生进行视力检查,并对其视力情况的数据进行整理和分析.视力情况共分4组:A.视力≥5.0,视力正常;B.视力=4.9,轻度视力不良;C.4.6≤视力≤4.8,中度视力不良;D.视力≤4.5,重度视力不良.下面给出了部分信息:
抽取的八年级学生的视力在C组的数据是:4.6,4.6,4.7,4.7,4.8,4.8;
抽取的九年级学生的视力在C组的数据是:4.6,4.7,4.8,4.7,4.7,4.8,4.7,4.7;
被抽取的八、九年级学生视力的平均数、中位数、众数如下表:
平均数 中位数 众数
八年级 4.82 a 4.9
九年级 4.82 4.8 4.7
(1)填空:a= 4.9 ,m= 20 ;
(2)根据以上数据分析,你认为该校八年级和九年级学生的视力情况谁更健康,请说明理由(写出一条理由即可);
(3)该校八年级共有学生500人,请估计八年级学生视力正常的人数.
【解答】解:(1)八年级学生的视力按从小到大的顺序排序后,第10个数据和第11个数据都是4.9,
∴a==4.9,
20×25%=5,20×%15=3,C组人数为8,
∴B组人数为20﹣5﹣3﹣8=4,
∴m%=100%=20%,
∴m=20,
故答案为:4.9,20;
(2)∵八年级和九年级学生的视力的平均数相等,而八年级学生的视力的中位数和众数均高于九年级,
∴八年级学生的视力情况谁更健康;
(3)500×=150(人),
估计八年级学生视力正常的人数为150人.
27.(2023秋 南开区期末)在△ABC中,∠C=90°,以边AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为的中点,⊙O的半径为2,求AB的长.
【解答】解:(1)连接OD,
∵OA为半径的圆与BC相切于点D,
∴OD⊥BC,
∴∠ODB=90°,
∵在△ABC中,∠C=90°,
∴∠ODB=∠C,
∴OD∥AC,
∴∠CAD=∠ADO=25°,
∵OA=OD,
∴∠OAD=∠ODA=25°,
∴∠BOD=2∠OAD=50°,
∴∠B=90°﹣∠BOD=40°;
(2)连接OF,OD,
由(1)得:OD∥AC,
∴∠AFO=∠FOD,
∵OA=OF,点F为的中点,
∴∠A=∠AFO,∠AOF=∠FOD,
∴∠A=∠AFO=∠AOF=60°,
∴∠B=90°﹣∠A=30°,
∵OA=OD=2,
∴OB=2OD=4,
∴AB=OA+OB=6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
