期末真题重组卷-2024-2025学年数学九年级上册北师大版(含解析)
文档属性
| 名称 | 期末真题重组卷-2024-2025学年数学九年级上册北师大版(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 887.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组卷-2024-2025学年数学九年级上册北师大版
一.选择题(共10小题)
1.(2023秋 滨海新区校级期末)如图的三视图对应的物体是( )
A. B.
C. D.
2.(2023秋 济阳区期末)如果,则=( )
A. B. C. D.
3.(2023秋 锦江区校级期末)在一个不透明的布袋中装有30个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.4左右,则布袋中白球可能有( )
A.12个 B.15个 C.18个 D.20个
4.(2023秋 东明县期末)点(﹣3,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(2,6) B.(3,4) C.(﹣6,﹣2) D.(﹣4,3)
5.(2023秋 东莞市期末)配方法解方程2x2﹣x﹣2=0应把它先变形为( )
A.(x﹣)2= B.(x﹣)2=0
C.(x﹣)2= D.(x﹣)2=
6.(2023秋 官渡区期末)2023年10月8日,杭州亚运会乒乓球比赛全部结束,国乒揽获除女双项目外的6块金牌,展现了我国乒乓球队员强大的实力.某小组赛采用单循环制(每两队之间都进行一场比赛),比赛总场数为28场.若设参赛队伍有x支,则可列方程为( )
A. B.x(x﹣1)=28
C.2x(x﹣1)=28 D.x2=28
7.(2023秋 南山区期末)如图,在平面直角坐标系xOy中,两个“E”字是位似图形,位似中心点O,①号“E”与②号“E”的位似比为2:1.点P(﹣6,9)在①号“E”上,则点P在②号“E”上的对应点Q的坐标为( )
A.(﹣3,) B.(﹣2,3) C.(﹣,3) D.(﹣3,2)
8.(2023秋 裕华区校级期末)如图,有一张长12cm,宽9cm的矩形纸片,在它的四个角各剪去一个同样大小的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是70cm2,求剪去的小正方形的边长.设剪去的小正方形的边长是xcm,根据题意,可列方程为( )
A.12×9﹣4×9x=70 B.12×9﹣4x2=70
C.(12﹣x)(9﹣x)=70 D.(12﹣2x)(9﹣2x)=70
9.(2023秋 梁溪区校级期末)如图,△ABC∽△ADE,S△ABC:S四边形BDEC=1:2,其中,DE的长为( )
A. B. C. D.6
10.(2023秋 泉州期末)甲、乙两人沿着如图所示的平行四边形空地边缘进行跑步比赛,两人同时从点B出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍.当甲到达点E,乙到达点F时,甲、乙的影子(太阳光照射)刚好在同一条直线上,此时,点B处一根杆子的影子(太阳光照射)刚好在对角线BD上,则CE的长为( )
A.4m B.8m C.12m D.16m
二.填空题(共8小题)
11.(2023秋 罗定市期末)若α,β是方程x2+2x﹣2026=0的两个实数根,则α2+3α+β的值为 .
12.(2023秋 新洲区期末)某数学兴趣小组做“任意抛掷一枚图钉”的重复试验,多次试验后获得如下数据:
重复试验次数 10 50 、100 500 1000
钉尖朝上次数 5 15 36 200 400
由此可以估计任意抛掷一次图钉,钉尖朝上的概率约为 .(结果精确到0.1)
13.(2023秋 上城区期末)如图,AC、BD交于点O,连接AB、CD,若要使△AOB∽△COD,可以添加条件 .(只需写出一个条件即可)
14.(2023秋 东辽县期末)如图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.6米,车头FACD近似看成一个矩形,且满足3FD=2FA,若盲区EB的长度是6米,则车宽FA的长度为 米.
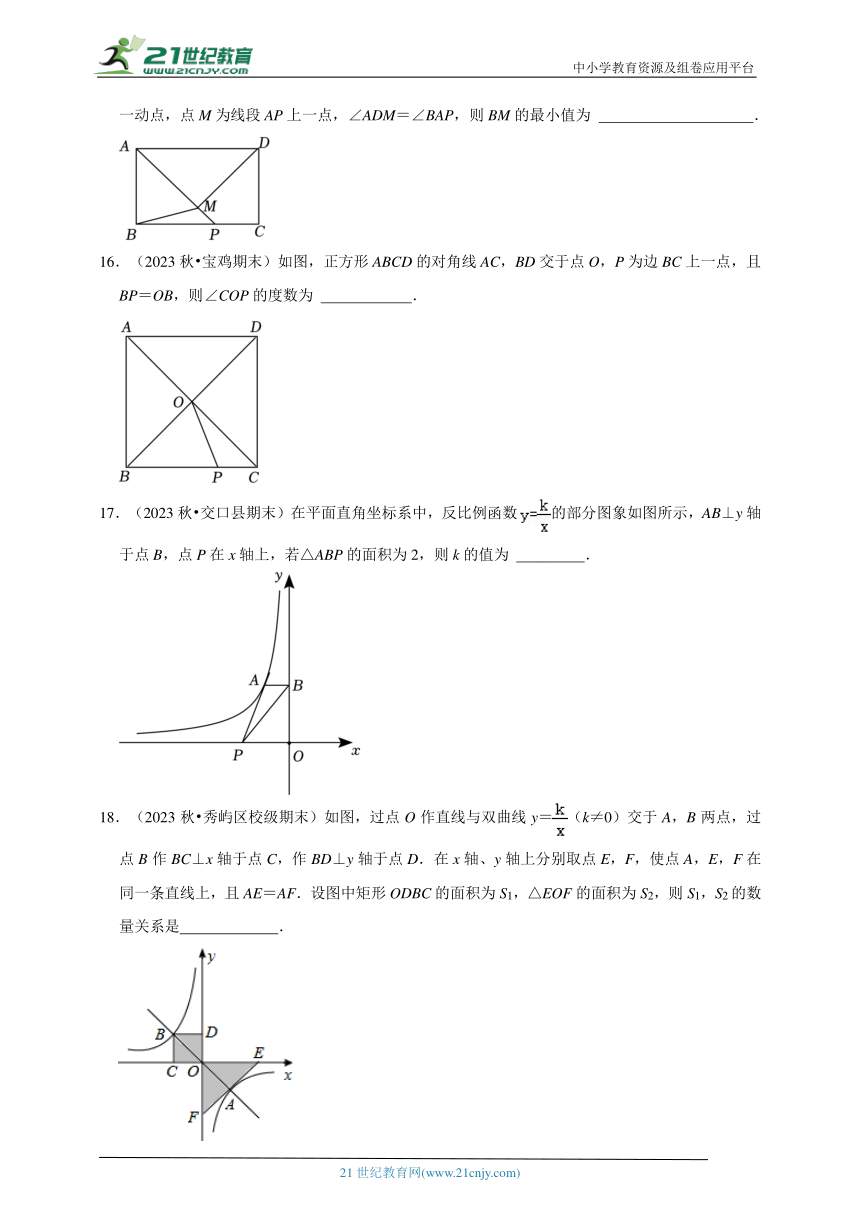
15.(2022秋 高新区校级期末)如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为 .
16.(2023秋 宝鸡期末)如图,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为 .
17.(2023秋 交口县期末)在平面直角坐标系中,反比例函数的部分图象如图所示,AB⊥y轴于点B,点P在x轴上,若△ABP的面积为2,则k的值为 .
18.(2023秋 秀屿区校级期末)如图,过点O作直线与双曲线y=(k≠0)交于A,B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴、y轴上分别取点E,F,使点A,E,F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1,S2的数量关系是 .
三.解答题(共9小题)
19.(2023秋 微山县期末)用适当的方法解下列方程:
(1)x2+5x﹣1=0;
(2)7x(5x+2)=6(5x+2);
20.(2023秋 和县期末)已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)若x=1是方程的一个根,求实数m的值;
(2)求证:方程总有两个不相等的实数根.
21.(2023秋 罗定市校级期末)早茶作为广东餐饮文化的重要组成部分,以其小吃精美、种类繁多、口味独特、价格实惠而闻名.张帆在广州旅游期间,决定在“A.虾饺,B.干蒸烧卖,C.艇仔粥,D.蜜汁叉烧包”四种茶点中选择喜欢的进行品尝.(选到每种茶点的可能性相同)
(1)如果只选其中一种茶点品尝,张帆选到“蜜汁叉烧包”的概率是 ;
(2)如果选择两种茶点品尝,请用画树状图或列表的方法求张帆选到“虾饺”和“艇仔粥”的概率.
22.(2023秋 临泉县期末)在《数书九章》(宋 秦九韶)中记载了一个测量塔高的问题:如图,AB表示塔的高度,CD表示竹竿顶端到地面的高度,EF表示人跟到地面的高度,AB、CD、EF在同一平面内,点A、C、E在一条水平直线上,已知AC=20米,CE=10米,CD=7米,EF=1.4米,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D.根据以上信息,求塔AB的高度.
23.(2023秋 上城区期末)如图,在四边形ABCD中,AD∥BC,点F,E分别在线段BC,AC上,且∠AFC=∠DEA,AC=AD.
(1)求证:DE=AF;
(2)若∠ABC=∠CDE,求证:AF2=BF CE.
24.(2023秋 济阳区期末)2022年9月,教育部正式印发《义务教育课程方案》,《劳动教育》成为一门独立的课程,某学校率先行动,在校园开辟了一块劳动教育基地:一面利用学校的墙(墙的最大可用长度为15米),用长为30米的篱笆,围成矩形养殖园如图1,已知矩形的边CD靠院墙,AD和BC与院墙垂直,设AB的长为x m.
(1)当围成的矩形养殖园面积为100m2时,求BC的长;
(2)如图2,该学校打算在养殖园饲养鸡、鸭、鹅三种家禽,需要在中间多加上两道篱笆作为隔离网,并与院墙垂直,请问此时养殖园的面积能否达到100m2?若能,求出AB的长;若不能,请说明理由.
25.(2023秋 福州期末)某校后勤处每周周日均会对学校教室进行消毒处理,已知消毒水的消毒效果随着时间变化如图所示,消毒效果y(单位:效力)与时间x(单位:分钟)呈现三段函数图象,其中AB段是渐消毒阶段,BC段为深消毒阶段,CD段是反比例函数图象的一部分,为降消毒阶段.请根据图中信息解答下列问题:
(1)求深消毒阶段和降消毒阶段中y与x之间的函数关系式;
(2)若消毒效果持续28分钟达到4效力及以上,即可产生消毒作用,请问本次消毒是否有效?
26.(2022秋 源城区校级期末)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)若AE=4,AD=5,求AC的长.
27.(2023秋 金牛区期末)如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数的图象交于A,C两点,与x轴、y轴分别交于点B,D,已知点A的坐标为(﹣2,4),点C的坐标为(8,m).
(1)求一次函数和反比例函数的解析式;
(2)若点M在x轴上,以M、A、B为顶点的三角形与△BOD相似时,求点M的坐标;
(3)点P是直线AB下方反比例函数图象上一点,当△PAB的面积为24时,求点P的坐标.
期末真题重组卷-2024-2025学年数学九年级上册北师大版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 滨海新区校级期末)如图的三视图对应的物体是( )
A. B.
C. D.
【解答】解:从俯视图可以看出直观图的下面部分为三个长方体,且三个长方体的宽度相同.只有D满足这两点,
故选:D.
2.(2023秋 济阳区期末)如果,则=( )
A. B. C. D.
【解答】解:∵,
∴=.
故选:C.
3.(2023秋 锦江区校级期末)在一个不透明的布袋中装有30个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.4左右,则布袋中白球可能有( )
A.12个 B.15个 C.18个 D.20个
【解答】解:设袋子中黄球有x个,
根据题意,得:,
解得:x=12,
则白球有30﹣12=18个;
故选:C.
4.(2023秋 东明县期末)点(﹣3,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(2,6) B.(3,4) C.(﹣6,﹣2) D.(﹣4,3)
【解答】解:∵点P(﹣3,4)在y=的图象上,
∴k=xy=(﹣3)×4=﹣12,
∵2×6=12≠﹣12,故选项A不符合题意,
∵3×4=12≠﹣12,故选项B不符合题意,
∵﹣6×(﹣2)=12≠﹣12,故选项C不符合题意,
∵﹣4×3=﹣12,故选项D符合题意,
故选:D.
5.(2023秋 东莞市期末)配方法解方程2x2﹣x﹣2=0应把它先变形为( )
A.(x﹣)2= B.(x﹣)2=0
C.(x﹣)2= D.(x﹣)2=
【解答】解:方程2x2﹣x﹣2=0变形得:x2﹣x=1,
配方得:x2﹣x+=,即(x﹣)2=.
故选:D.
6.(2023秋 官渡区期末)2023年10月8日,杭州亚运会乒乓球比赛全部结束,国乒揽获除女双项目外的6块金牌,展现了我国乒乓球队员强大的实力.某小组赛采用单循环制(每两队之间都进行一场比赛),比赛总场数为28场.若设参赛队伍有x支,则可列方程为( )
A. B.x(x﹣1)=28
C.2x(x﹣1)=28 D.x2=28
【解答】解:设参赛队伍有x支,则每只参赛队伍参加(x﹣1)场比赛,
根据题意得:,
故选:A.
7.(2023秋 南山区期末)如图,在平面直角坐标系xOy中,两个“E”字是位似图形,位似中心点O,①号“E”与②号“E”的位似比为2:1.点P(﹣6,9)在①号“E”上,则点P在②号“E”上的对应点Q的坐标为( )
A.(﹣3,) B.(﹣2,3) C.(﹣,3) D.(﹣3,2)
【解答】解:∵①号“E”与②号“E”是位似图形,位似比为2:1,点P(﹣6,9),
∴点P在②号“E”上的对应点Q的坐标为(﹣6×,9×),即(﹣3,),
故选:A.
8.(2023秋 裕华区校级期末)如图,有一张长12cm,宽9cm的矩形纸片,在它的四个角各剪去一个同样大小的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是70cm2,求剪去的小正方形的边长.设剪去的小正方形的边长是xcm,根据题意,可列方程为( )
A.12×9﹣4×9x=70 B.12×9﹣4x2=70
C.(12﹣x)(9﹣x)=70 D.(12﹣2x)(9﹣2x)=70
【解答】解:设剪去的小正方形的边长是x cm,则纸盒底面的长为(12﹣2x)cm,宽为(9﹣2x)cm,
∵纸盒的底面(图中阴影部分)面积是70cm2,
∴(12﹣2x)(9﹣2x)=70,
故选:D.
9.(2023秋 梁溪区校级期末)如图,△ABC∽△ADE,S△ABC:S四边形BDEC=1:2,其中,DE的长为( )
A. B. C. D.6
【解答】解:∵S△ABC:S四边形BDEC=1:2,
∴S△ABC:S△ADE=1:3,
∵△ABC∽△ADE,
∴=,
∵CB=,
∴DE=.
故选:A.
10.(2023秋 泉州期末)甲、乙两人沿着如图所示的平行四边形空地边缘进行跑步比赛,两人同时从点B出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍.当甲到达点E,乙到达点F时,甲、乙的影子(太阳光照射)刚好在同一条直线上,此时,点B处一根杆子的影子(太阳光照射)刚好在对角线BD上,则CE的长为( )
A.4m B.8m C.12m D.16m
【解答】解:连接EF,
∵甲、乙的影子(太阳光照射)刚好在同一条直线上,此时,点B处一根杆子的影子(太阳光照射)刚好在对角线BD上,
∴EF∥BD,
∴△CEF∽△CDB,
∴,
∵两人同时从点B出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍.
∴BC+CE=2BF=40+CE,
∴BF=(40+CE)=20+CE,
∴CF=40﹣20﹣CE=20﹣CE,
∴,
∴CE=8(m),
故选:B.
二.填空题(共8小题)
11.(2023秋 罗定市期末)若α,β是方程x2+2x﹣2026=0的两个实数根,则α2+3α+β的值为 2024 .
【解答】解:∵α,β是方程x2+2x﹣2026=0的两个实数根,
∴α+β=﹣2,α2+2α﹣2026=0,
∴α2+2α=2026,
∴α2+3α+β
=(α2+2α)+(α+β)
=2026+(﹣2)
=2024,
故答案为:2024.
12.(2023秋 新洲区期末)某数学兴趣小组做“任意抛掷一枚图钉”的重复试验,多次试验后获得如下数据:
重复试验次数 10 50 、100 500 1000
钉尖朝上次数 5 15 36 200 400
由此可以估计任意抛掷一次图钉,钉尖朝上的概率约为 0.4 .(结果精确到0.1)
【解答】解:表中图钉钉尖朝上的频率分别为5÷10=0.5,15÷50=0.3,36÷100=0.36,200÷500=0.4,400÷1000=0.4,
图钉钉尖朝上频率逐渐稳定在0.4左右,
估计任意抛掷一枚图钉,图钉钉尖朝上的概率约为0.4.
故答案为:0.4.
13.(2023秋 上城区期末)如图,AC、BD交于点O,连接AB、CD,若要使△AOB∽△COD,可以添加条件 ∠A=∠C(答案不唯一) .(只需写出一个条件即可)
【解答】解:添加∠A=∠C,且∠AOB=∠COD,
∴△AOB∽△COD,
故答案为:∠A=∠C(答案不唯一).
14.(2023秋 东辽县期末)如图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.6米,车头FACD近似看成一个矩形,且满足3FD=2FA,若盲区EB的长度是6米,则车宽FA的长度为 米.
【解答】解:如图,过点P作PQ⊥BE,交AF于点M,由于3FD=2FA,可是AF=x米,则DF=x米,
∵四边形ACDF是矩形,
∴AF∥CD,
∴△PAF∽△PBE,
∴=,
即=.
解得x=,
即AF=米,
故答案为:.
15.(2022秋 高新区校级期末)如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为 ﹣2 .
【解答】解:如图,取AD的中点O,连接OB,OM.
∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC=4,
∴∠BAP+∠DAM=90°,
∵∠ADM=∠BAP,
∴∠ADM+∠DAM=90°,
∴∠AMD=90°,
∵AO=OD=2,
∴OM=AD=2,
∴点M在以O为圆心,2为半径的⊙O上,
∵OB===,
∴BM≥OB﹣OM=﹣2,
∴BM的最小值为﹣2.
故答案为:﹣2.
16.(2023秋 宝鸡期末)如图,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为 22.5° .
【解答】解:∵四边形ABCD是正方形,
∴∠BOC=90°,∠OBC=45°,
∵BP=OB,
∴∠BOP=∠BPO=(180°﹣45°)=67.5°,
∴∠COP=90°﹣67.5°=22.5°.
故答案为:22.5°.
17.(2023秋 交口县期末)在平面直角坐标系中,反比例函数的部分图象如图所示,AB⊥y轴于点B,点P在x轴上,若△ABP的面积为2,则k的值为 ﹣4 .
【解答】解:∵AB⊥y轴,
∴AB∥x轴,
∴S△AOB=S△ABP=2,
∵S△AOB=|k|,
∴|k|=4,
∵反比例函数y=在第二象限,
∴k=﹣4,
故答案为:﹣4.
18.(2023秋 秀屿区校级期末)如图,过点O作直线与双曲线y=(k≠0)交于A,B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴、y轴上分别取点E,F,使点A,E,F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1,S2的数量关系是 2S1=S2 .
【解答】解:过点A作AM⊥x轴于点M,如图所示.
∵AM⊥x轴,BC⊥x轴,BD⊥y轴,
∴S矩形ODBC=﹣k,S△AOM=﹣k.
∵AE=AF.OF⊥x轴,AM⊥x轴,
∴AM=OF,ME=OM=OE,
∴S△EOF=OE OF=4S△AOM=﹣2k,
∴2S矩形ODBC=S△EOF,
即2S1=S2.
故答案为:2S1=S2.
三.解答题(共9小题)
19.(2023秋 微山县期末)用适当的方法解下列方程:
(1)x2+5x﹣1=0;
(2)7x(5x+2)=6(5x+2);
【解答】解(1)∵x2+5x﹣1=0,
∴a=1,b=5,c=﹣1,
∴Δ=b2﹣4ac=52﹣4×1×(﹣1)=29>0,
∴,
解得;
(2)∵7x(5x+2)=6(5x+2),
∴7x(5x+2)﹣6(5x+2)=0,
∴(7x﹣6)(5x+2)=0,
∴7x﹣6=0或5x+2=0,
解得;
20.(2023秋 和县期末)已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)若x=1是方程的一个根,求实数m的值;
(2)求证:方程总有两个不相等的实数根.
【解答】(1)解:将x=1代入原式,得1+(m+3)+m+1=0;
解得m=﹣;
(2)证明:∵Δ=(m+3)2﹣4(m+1)=(m+1)2+4>0,
∴原方程总有两个不相等的实数根;
21.(2023秋 罗定市校级期末)早茶作为广东餐饮文化的重要组成部分,以其小吃精美、种类繁多、口味独特、价格实惠而闻名.张帆在广州旅游期间,决定在“A.虾饺,B.干蒸烧卖,C.艇仔粥,D.蜜汁叉烧包”四种茶点中选择喜欢的进行品尝.(选到每种茶点的可能性相同)
(1)如果只选其中一种茶点品尝,张帆选到“蜜汁叉烧包”的概率是 ;
(2)如果选择两种茶点品尝,请用画树状图或列表的方法求张帆选到“虾饺”和“艇仔粥”的概率.
【解答】解:(1)∵共有四种茶点,
∴如果只选其中一种茶点品尝,张帆选到“蜜汁叉烧包”的概率是:,
故答案为:;
(2)画树状图如图所示:
由树状图知,共有12种可能出现的结果,且每种结果出现的可能性相等,其中选到“虾饺”和“艇仔粥”的结果有2种,
∴P(张帆选到“虾饺”和“艇仔粥”)=.
22.(2023秋 临泉县期末)在《数书九章》(宋 秦九韶)中记载了一个测量塔高的问题:如图,AB表示塔的高度,CD表示竹竿顶端到地面的高度,EF表示人跟到地面的高度,AB、CD、EF在同一平面内,点A、C、E在一条水平直线上,已知AC=20米,CE=10米,CD=7米,EF=1.4米,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D.根据以上信息,求塔AB的高度.
【解答】解:过点F作FG⊥CD,垂足为G,延长FG交AB于点H,
由题意得:FH⊥AB,AH=CG=EF=1.4米,AC=GH=20米,CE=FG=10米,
∴∠DGF=∠BHF=90°,
∵CD=7米,
∴DG=CD﹣CG=7﹣1.4=5.6(米),
∵∠DFG=∠BFH,
∴△FDG∽△FBH,
∴,
∴,
∴BH=16.8,
∴AB=BH+AH=16.8+1.4=18.2(米),
∴塔的高度为18.2米.
23.(2023秋 上城区期末)如图,在四边形ABCD中,AD∥BC,点F,E分别在线段BC,AC上,且∠AFC=∠DEA,AC=AD.
(1)求证:DE=AF;
(2)若∠ABC=∠CDE,求证:AF2=BF CE.
【解答】证明:(1)∵AD∥BC,
∴∠ACF=∠DAC
∵∠AFC=∠DEA,AC=AD,
∴△ACF≌△DAE(AAS),
∴AF=DE;
(2)∵△ACF≌△DAE,
∴∠AFC=∠DEA,
∴∠AFB=∠DEC,
∵∠ABC=∠CDE,
∴△ABF∽△CDE,
∴=,
∴AF DE=BF CE,
∵AF=DE,
∴AF2=BF CE.
24.(2023秋 济阳区期末)2022年9月,教育部正式印发《义务教育课程方案》,《劳动教育》成为一门独立的课程,某学校率先行动,在校园开辟了一块劳动教育基地:一面利用学校的墙(墙的最大可用长度为15米),用长为30米的篱笆,围成矩形养殖园如图1,已知矩形的边CD靠院墙,AD和BC与院墙垂直,设AB的长为x m.
(1)当围成的矩形养殖园面积为100m2时,求BC的长;
(2)如图2,该学校打算在养殖园饲养鸡、鸭、鹅三种家禽,需要在中间多加上两道篱笆作为隔离网,并与院墙垂直,请问此时养殖园的面积能否达到100m2?若能,求出AB的长;若不能,请说明理由.
【解答】解:(1)设AB的长为x m,则矩形的宽BC=(30﹣x)m,
由题意得:x×(30﹣x)=100,
解得 x1=10,x2=20,
∵墙的最大可用长度为15米,
∴0<x≤15,
∴x=10,
即BC的长为10m;
(2)养殖园的面积不能达到100m2,理由如下:
假设养殖园的面积能达到100m2,设AB的长为y m,则BC的长为m,
根据题意得:y =100,
整理得:y2﹣30y+400=0,
∵Δ=(﹣30)2﹣4×1×400=﹣700<0,
∴原方程没有实数根,
∴假设不成立,即养殖园的面积不能达到100m2.
25.(2023秋 福州期末)某校后勤处每周周日均会对学校教室进行消毒处理,已知消毒水的消毒效果随着时间变化如图所示,消毒效果y(单位:效力)与时间x(单位:分钟)呈现三段函数图象,其中AB段是渐消毒阶段,BC段为深消毒阶段,CD段是反比例函数图象的一部分,为降消毒阶段.请根据图中信息解答下列问题:
(1)求深消毒阶段和降消毒阶段中y与x之间的函数关系式;
(2)若消毒效果持续28分钟达到4效力及以上,即可产生消毒作用,请问本次消毒是否有效?
【解答】解:(1)设BC段的函数解析式为y=kx+b,
把(10,3)和(30,6)代入得,
解得,
∴BC段的函数解析式为y=x+,
设CD段的函数解析式为y=,
把(30,6)代入得6=,
∴m=180,
∴CD段的函数解析式为y=;
(2)把y=4分别代入y=x+和y=得,
x=或x=45,
∵45﹣=28>28,
∴本次消毒有效.
26.(2022秋 源城区校级期末)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)若AE=4,AD=5,求AC的长.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC.
∵CF∥AE,
∴四边形AECF是平行四边形.
∵AE⊥BC,
∴∠AEC=90°,
∴平行四边形AECF是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=BC=5,OA=OC,AC⊥BD,
∵AE⊥BC,
∴∠AEB=90°,
∴,
∴CE=BE+BC=3+5=8,
∴.
27.(2023秋 金牛区期末)如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数的图象交于A,C两点,与x轴、y轴分别交于点B,D,已知点A的坐标为(﹣2,4),点C的坐标为(8,m).
(1)求一次函数和反比例函数的解析式;
(2)若点M在x轴上,以M、A、B为顶点的三角形与△BOD相似时,求点M的坐标;
(3)点P是直线AB下方反比例函数图象上一点,当△PAB的面积为24时,求点P的坐标.
【解答】解:(1)把点A(﹣2,4)代入得k=﹣2×4=﹣8,
∴反比例函数的解析式为y=﹣;
把(8,m)代入y=﹣得m=﹣=﹣1,
∴点C的坐标为(8,﹣1),
把A(﹣2,4)和点C(8,﹣1)代入,
解得,
∴一次函数的解析式为y=﹣x+3;
(2)设M(m,0),
在y=﹣x+3中,令x=0,则y=3,令y=0,则x=6,
∴D(0,3),B(6,0),
∴OD=3,OB=8,
∵以M、A、B为顶点的三角形与△BOD相似,
∴∠MAB=∠BOD=90°,
∴△ABM∽△DBO,
∴,
∵AM=,AB==4,BM=6﹣m,
∴=,
解得m=﹣4,m=0(不合题意舍去),
当∠AMB=∠BOD=90°,AM∥OD,
∴△AMB∽△DOB,
∴AM⊥x轴,
∴OM=2
即m=﹣2,
∴点M的坐标为(﹣4,0)或(﹣2,0);
(3)设点P的坐标为(n,﹣),
∵A(﹣2,4),B(6,0),
当点P在第四象限时,△PAB的面积=[6﹣(﹣2)]×[4﹣(﹣)]﹣×8×4﹣(4+)(n+2)﹣××(6﹣n)=24,
解得n=2,n=﹣8(不合题意舍去),
当点P在第二象限时,△PAB的面积=(4++4)(6﹣n)﹣×8×4﹣×(﹣2﹣n)(4+)=24,
解得n=﹣8,n=2(不合题意舍去)
综上所述,点P的坐标为(2,﹣4)或(﹣8,1).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组卷-2024-2025学年数学九年级上册北师大版
一.选择题(共10小题)
1.(2023秋 滨海新区校级期末)如图的三视图对应的物体是( )
A. B.
C. D.
2.(2023秋 济阳区期末)如果,则=( )
A. B. C. D.
3.(2023秋 锦江区校级期末)在一个不透明的布袋中装有30个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.4左右,则布袋中白球可能有( )
A.12个 B.15个 C.18个 D.20个
4.(2023秋 东明县期末)点(﹣3,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(2,6) B.(3,4) C.(﹣6,﹣2) D.(﹣4,3)
5.(2023秋 东莞市期末)配方法解方程2x2﹣x﹣2=0应把它先变形为( )
A.(x﹣)2= B.(x﹣)2=0
C.(x﹣)2= D.(x﹣)2=
6.(2023秋 官渡区期末)2023年10月8日,杭州亚运会乒乓球比赛全部结束,国乒揽获除女双项目外的6块金牌,展现了我国乒乓球队员强大的实力.某小组赛采用单循环制(每两队之间都进行一场比赛),比赛总场数为28场.若设参赛队伍有x支,则可列方程为( )
A. B.x(x﹣1)=28
C.2x(x﹣1)=28 D.x2=28
7.(2023秋 南山区期末)如图,在平面直角坐标系xOy中,两个“E”字是位似图形,位似中心点O,①号“E”与②号“E”的位似比为2:1.点P(﹣6,9)在①号“E”上,则点P在②号“E”上的对应点Q的坐标为( )
A.(﹣3,) B.(﹣2,3) C.(﹣,3) D.(﹣3,2)
8.(2023秋 裕华区校级期末)如图,有一张长12cm,宽9cm的矩形纸片,在它的四个角各剪去一个同样大小的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是70cm2,求剪去的小正方形的边长.设剪去的小正方形的边长是xcm,根据题意,可列方程为( )
A.12×9﹣4×9x=70 B.12×9﹣4x2=70
C.(12﹣x)(9﹣x)=70 D.(12﹣2x)(9﹣2x)=70
9.(2023秋 梁溪区校级期末)如图,△ABC∽△ADE,S△ABC:S四边形BDEC=1:2,其中,DE的长为( )
A. B. C. D.6
10.(2023秋 泉州期末)甲、乙两人沿着如图所示的平行四边形空地边缘进行跑步比赛,两人同时从点B出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍.当甲到达点E,乙到达点F时,甲、乙的影子(太阳光照射)刚好在同一条直线上,此时,点B处一根杆子的影子(太阳光照射)刚好在对角线BD上,则CE的长为( )
A.4m B.8m C.12m D.16m
二.填空题(共8小题)
11.(2023秋 罗定市期末)若α,β是方程x2+2x﹣2026=0的两个实数根,则α2+3α+β的值为 .
12.(2023秋 新洲区期末)某数学兴趣小组做“任意抛掷一枚图钉”的重复试验,多次试验后获得如下数据:
重复试验次数 10 50 、100 500 1000
钉尖朝上次数 5 15 36 200 400
由此可以估计任意抛掷一次图钉,钉尖朝上的概率约为 .(结果精确到0.1)
13.(2023秋 上城区期末)如图,AC、BD交于点O,连接AB、CD,若要使△AOB∽△COD,可以添加条件 .(只需写出一个条件即可)
14.(2023秋 东辽县期末)如图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.6米,车头FACD近似看成一个矩形,且满足3FD=2FA,若盲区EB的长度是6米,则车宽FA的长度为 米.
15.(2022秋 高新区校级期末)如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为 .
16.(2023秋 宝鸡期末)如图,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为 .
17.(2023秋 交口县期末)在平面直角坐标系中,反比例函数的部分图象如图所示,AB⊥y轴于点B,点P在x轴上,若△ABP的面积为2,则k的值为 .
18.(2023秋 秀屿区校级期末)如图,过点O作直线与双曲线y=(k≠0)交于A,B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴、y轴上分别取点E,F,使点A,E,F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1,S2的数量关系是 .
三.解答题(共9小题)
19.(2023秋 微山县期末)用适当的方法解下列方程:
(1)x2+5x﹣1=0;
(2)7x(5x+2)=6(5x+2);
20.(2023秋 和县期末)已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)若x=1是方程的一个根,求实数m的值;
(2)求证:方程总有两个不相等的实数根.
21.(2023秋 罗定市校级期末)早茶作为广东餐饮文化的重要组成部分,以其小吃精美、种类繁多、口味独特、价格实惠而闻名.张帆在广州旅游期间,决定在“A.虾饺,B.干蒸烧卖,C.艇仔粥,D.蜜汁叉烧包”四种茶点中选择喜欢的进行品尝.(选到每种茶点的可能性相同)
(1)如果只选其中一种茶点品尝,张帆选到“蜜汁叉烧包”的概率是 ;
(2)如果选择两种茶点品尝,请用画树状图或列表的方法求张帆选到“虾饺”和“艇仔粥”的概率.
22.(2023秋 临泉县期末)在《数书九章》(宋 秦九韶)中记载了一个测量塔高的问题:如图,AB表示塔的高度,CD表示竹竿顶端到地面的高度,EF表示人跟到地面的高度,AB、CD、EF在同一平面内,点A、C、E在一条水平直线上,已知AC=20米,CE=10米,CD=7米,EF=1.4米,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D.根据以上信息,求塔AB的高度.
23.(2023秋 上城区期末)如图,在四边形ABCD中,AD∥BC,点F,E分别在线段BC,AC上,且∠AFC=∠DEA,AC=AD.
(1)求证:DE=AF;
(2)若∠ABC=∠CDE,求证:AF2=BF CE.
24.(2023秋 济阳区期末)2022年9月,教育部正式印发《义务教育课程方案》,《劳动教育》成为一门独立的课程,某学校率先行动,在校园开辟了一块劳动教育基地:一面利用学校的墙(墙的最大可用长度为15米),用长为30米的篱笆,围成矩形养殖园如图1,已知矩形的边CD靠院墙,AD和BC与院墙垂直,设AB的长为x m.
(1)当围成的矩形养殖园面积为100m2时,求BC的长;
(2)如图2,该学校打算在养殖园饲养鸡、鸭、鹅三种家禽,需要在中间多加上两道篱笆作为隔离网,并与院墙垂直,请问此时养殖园的面积能否达到100m2?若能,求出AB的长;若不能,请说明理由.
25.(2023秋 福州期末)某校后勤处每周周日均会对学校教室进行消毒处理,已知消毒水的消毒效果随着时间变化如图所示,消毒效果y(单位:效力)与时间x(单位:分钟)呈现三段函数图象,其中AB段是渐消毒阶段,BC段为深消毒阶段,CD段是反比例函数图象的一部分,为降消毒阶段.请根据图中信息解答下列问题:
(1)求深消毒阶段和降消毒阶段中y与x之间的函数关系式;
(2)若消毒效果持续28分钟达到4效力及以上,即可产生消毒作用,请问本次消毒是否有效?
26.(2022秋 源城区校级期末)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)若AE=4,AD=5,求AC的长.
27.(2023秋 金牛区期末)如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数的图象交于A,C两点,与x轴、y轴分别交于点B,D,已知点A的坐标为(﹣2,4),点C的坐标为(8,m).
(1)求一次函数和反比例函数的解析式;
(2)若点M在x轴上,以M、A、B为顶点的三角形与△BOD相似时,求点M的坐标;
(3)点P是直线AB下方反比例函数图象上一点,当△PAB的面积为24时,求点P的坐标.
期末真题重组卷-2024-2025学年数学九年级上册北师大版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 滨海新区校级期末)如图的三视图对应的物体是( )
A. B.
C. D.
【解答】解:从俯视图可以看出直观图的下面部分为三个长方体,且三个长方体的宽度相同.只有D满足这两点,
故选:D.
2.(2023秋 济阳区期末)如果,则=( )
A. B. C. D.
【解答】解:∵,
∴=.
故选:C.
3.(2023秋 锦江区校级期末)在一个不透明的布袋中装有30个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.4左右,则布袋中白球可能有( )
A.12个 B.15个 C.18个 D.20个
【解答】解:设袋子中黄球有x个,
根据题意,得:,
解得:x=12,
则白球有30﹣12=18个;
故选:C.
4.(2023秋 东明县期末)点(﹣3,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(2,6) B.(3,4) C.(﹣6,﹣2) D.(﹣4,3)
【解答】解:∵点P(﹣3,4)在y=的图象上,
∴k=xy=(﹣3)×4=﹣12,
∵2×6=12≠﹣12,故选项A不符合题意,
∵3×4=12≠﹣12,故选项B不符合题意,
∵﹣6×(﹣2)=12≠﹣12,故选项C不符合题意,
∵﹣4×3=﹣12,故选项D符合题意,
故选:D.
5.(2023秋 东莞市期末)配方法解方程2x2﹣x﹣2=0应把它先变形为( )
A.(x﹣)2= B.(x﹣)2=0
C.(x﹣)2= D.(x﹣)2=
【解答】解:方程2x2﹣x﹣2=0变形得:x2﹣x=1,
配方得:x2﹣x+=,即(x﹣)2=.
故选:D.
6.(2023秋 官渡区期末)2023年10月8日,杭州亚运会乒乓球比赛全部结束,国乒揽获除女双项目外的6块金牌,展现了我国乒乓球队员强大的实力.某小组赛采用单循环制(每两队之间都进行一场比赛),比赛总场数为28场.若设参赛队伍有x支,则可列方程为( )
A. B.x(x﹣1)=28
C.2x(x﹣1)=28 D.x2=28
【解答】解:设参赛队伍有x支,则每只参赛队伍参加(x﹣1)场比赛,
根据题意得:,
故选:A.
7.(2023秋 南山区期末)如图,在平面直角坐标系xOy中,两个“E”字是位似图形,位似中心点O,①号“E”与②号“E”的位似比为2:1.点P(﹣6,9)在①号“E”上,则点P在②号“E”上的对应点Q的坐标为( )
A.(﹣3,) B.(﹣2,3) C.(﹣,3) D.(﹣3,2)
【解答】解:∵①号“E”与②号“E”是位似图形,位似比为2:1,点P(﹣6,9),
∴点P在②号“E”上的对应点Q的坐标为(﹣6×,9×),即(﹣3,),
故选:A.
8.(2023秋 裕华区校级期末)如图,有一张长12cm,宽9cm的矩形纸片,在它的四个角各剪去一个同样大小的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是70cm2,求剪去的小正方形的边长.设剪去的小正方形的边长是xcm,根据题意,可列方程为( )
A.12×9﹣4×9x=70 B.12×9﹣4x2=70
C.(12﹣x)(9﹣x)=70 D.(12﹣2x)(9﹣2x)=70
【解答】解:设剪去的小正方形的边长是x cm,则纸盒底面的长为(12﹣2x)cm,宽为(9﹣2x)cm,
∵纸盒的底面(图中阴影部分)面积是70cm2,
∴(12﹣2x)(9﹣2x)=70,
故选:D.
9.(2023秋 梁溪区校级期末)如图,△ABC∽△ADE,S△ABC:S四边形BDEC=1:2,其中,DE的长为( )
A. B. C. D.6
【解答】解:∵S△ABC:S四边形BDEC=1:2,
∴S△ABC:S△ADE=1:3,
∵△ABC∽△ADE,
∴=,
∵CB=,
∴DE=.
故选:A.
10.(2023秋 泉州期末)甲、乙两人沿着如图所示的平行四边形空地边缘进行跑步比赛,两人同时从点B出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍.当甲到达点E,乙到达点F时,甲、乙的影子(太阳光照射)刚好在同一条直线上,此时,点B处一根杆子的影子(太阳光照射)刚好在对角线BD上,则CE的长为( )
A.4m B.8m C.12m D.16m
【解答】解:连接EF,
∵甲、乙的影子(太阳光照射)刚好在同一条直线上,此时,点B处一根杆子的影子(太阳光照射)刚好在对角线BD上,
∴EF∥BD,
∴△CEF∽△CDB,
∴,
∵两人同时从点B出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍.
∴BC+CE=2BF=40+CE,
∴BF=(40+CE)=20+CE,
∴CF=40﹣20﹣CE=20﹣CE,
∴,
∴CE=8(m),
故选:B.
二.填空题(共8小题)
11.(2023秋 罗定市期末)若α,β是方程x2+2x﹣2026=0的两个实数根,则α2+3α+β的值为 2024 .
【解答】解:∵α,β是方程x2+2x﹣2026=0的两个实数根,
∴α+β=﹣2,α2+2α﹣2026=0,
∴α2+2α=2026,
∴α2+3α+β
=(α2+2α)+(α+β)
=2026+(﹣2)
=2024,
故答案为:2024.
12.(2023秋 新洲区期末)某数学兴趣小组做“任意抛掷一枚图钉”的重复试验,多次试验后获得如下数据:
重复试验次数 10 50 、100 500 1000
钉尖朝上次数 5 15 36 200 400
由此可以估计任意抛掷一次图钉,钉尖朝上的概率约为 0.4 .(结果精确到0.1)
【解答】解:表中图钉钉尖朝上的频率分别为5÷10=0.5,15÷50=0.3,36÷100=0.36,200÷500=0.4,400÷1000=0.4,
图钉钉尖朝上频率逐渐稳定在0.4左右,
估计任意抛掷一枚图钉,图钉钉尖朝上的概率约为0.4.
故答案为:0.4.
13.(2023秋 上城区期末)如图,AC、BD交于点O,连接AB、CD,若要使△AOB∽△COD,可以添加条件 ∠A=∠C(答案不唯一) .(只需写出一个条件即可)
【解答】解:添加∠A=∠C,且∠AOB=∠COD,
∴△AOB∽△COD,
故答案为:∠A=∠C(答案不唯一).
14.(2023秋 东辽县期末)如图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.6米,车头FACD近似看成一个矩形,且满足3FD=2FA,若盲区EB的长度是6米,则车宽FA的长度为 米.
【解答】解:如图,过点P作PQ⊥BE,交AF于点M,由于3FD=2FA,可是AF=x米,则DF=x米,
∵四边形ACDF是矩形,
∴AF∥CD,
∴△PAF∽△PBE,
∴=,
即=.
解得x=,
即AF=米,
故答案为:.
15.(2022秋 高新区校级期末)如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为 ﹣2 .
【解答】解:如图,取AD的中点O,连接OB,OM.
∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC=4,
∴∠BAP+∠DAM=90°,
∵∠ADM=∠BAP,
∴∠ADM+∠DAM=90°,
∴∠AMD=90°,
∵AO=OD=2,
∴OM=AD=2,
∴点M在以O为圆心,2为半径的⊙O上,
∵OB===,
∴BM≥OB﹣OM=﹣2,
∴BM的最小值为﹣2.
故答案为:﹣2.
16.(2023秋 宝鸡期末)如图,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为 22.5° .
【解答】解:∵四边形ABCD是正方形,
∴∠BOC=90°,∠OBC=45°,
∵BP=OB,
∴∠BOP=∠BPO=(180°﹣45°)=67.5°,
∴∠COP=90°﹣67.5°=22.5°.
故答案为:22.5°.
17.(2023秋 交口县期末)在平面直角坐标系中,反比例函数的部分图象如图所示,AB⊥y轴于点B,点P在x轴上,若△ABP的面积为2,则k的值为 ﹣4 .
【解答】解:∵AB⊥y轴,
∴AB∥x轴,
∴S△AOB=S△ABP=2,
∵S△AOB=|k|,
∴|k|=4,
∵反比例函数y=在第二象限,
∴k=﹣4,
故答案为:﹣4.
18.(2023秋 秀屿区校级期末)如图,过点O作直线与双曲线y=(k≠0)交于A,B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴、y轴上分别取点E,F,使点A,E,F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1,S2的数量关系是 2S1=S2 .
【解答】解:过点A作AM⊥x轴于点M,如图所示.
∵AM⊥x轴,BC⊥x轴,BD⊥y轴,
∴S矩形ODBC=﹣k,S△AOM=﹣k.
∵AE=AF.OF⊥x轴,AM⊥x轴,
∴AM=OF,ME=OM=OE,
∴S△EOF=OE OF=4S△AOM=﹣2k,
∴2S矩形ODBC=S△EOF,
即2S1=S2.
故答案为:2S1=S2.
三.解答题(共9小题)
19.(2023秋 微山县期末)用适当的方法解下列方程:
(1)x2+5x﹣1=0;
(2)7x(5x+2)=6(5x+2);
【解答】解(1)∵x2+5x﹣1=0,
∴a=1,b=5,c=﹣1,
∴Δ=b2﹣4ac=52﹣4×1×(﹣1)=29>0,
∴,
解得;
(2)∵7x(5x+2)=6(5x+2),
∴7x(5x+2)﹣6(5x+2)=0,
∴(7x﹣6)(5x+2)=0,
∴7x﹣6=0或5x+2=0,
解得;
20.(2023秋 和县期末)已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)若x=1是方程的一个根,求实数m的值;
(2)求证:方程总有两个不相等的实数根.
【解答】(1)解:将x=1代入原式,得1+(m+3)+m+1=0;
解得m=﹣;
(2)证明:∵Δ=(m+3)2﹣4(m+1)=(m+1)2+4>0,
∴原方程总有两个不相等的实数根;
21.(2023秋 罗定市校级期末)早茶作为广东餐饮文化的重要组成部分,以其小吃精美、种类繁多、口味独特、价格实惠而闻名.张帆在广州旅游期间,决定在“A.虾饺,B.干蒸烧卖,C.艇仔粥,D.蜜汁叉烧包”四种茶点中选择喜欢的进行品尝.(选到每种茶点的可能性相同)
(1)如果只选其中一种茶点品尝,张帆选到“蜜汁叉烧包”的概率是 ;
(2)如果选择两种茶点品尝,请用画树状图或列表的方法求张帆选到“虾饺”和“艇仔粥”的概率.
【解答】解:(1)∵共有四种茶点,
∴如果只选其中一种茶点品尝,张帆选到“蜜汁叉烧包”的概率是:,
故答案为:;
(2)画树状图如图所示:
由树状图知,共有12种可能出现的结果,且每种结果出现的可能性相等,其中选到“虾饺”和“艇仔粥”的结果有2种,
∴P(张帆选到“虾饺”和“艇仔粥”)=.
22.(2023秋 临泉县期末)在《数书九章》(宋 秦九韶)中记载了一个测量塔高的问题:如图,AB表示塔的高度,CD表示竹竿顶端到地面的高度,EF表示人跟到地面的高度,AB、CD、EF在同一平面内,点A、C、E在一条水平直线上,已知AC=20米,CE=10米,CD=7米,EF=1.4米,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D.根据以上信息,求塔AB的高度.
【解答】解:过点F作FG⊥CD,垂足为G,延长FG交AB于点H,
由题意得:FH⊥AB,AH=CG=EF=1.4米,AC=GH=20米,CE=FG=10米,
∴∠DGF=∠BHF=90°,
∵CD=7米,
∴DG=CD﹣CG=7﹣1.4=5.6(米),
∵∠DFG=∠BFH,
∴△FDG∽△FBH,
∴,
∴,
∴BH=16.8,
∴AB=BH+AH=16.8+1.4=18.2(米),
∴塔的高度为18.2米.
23.(2023秋 上城区期末)如图,在四边形ABCD中,AD∥BC,点F,E分别在线段BC,AC上,且∠AFC=∠DEA,AC=AD.
(1)求证:DE=AF;
(2)若∠ABC=∠CDE,求证:AF2=BF CE.
【解答】证明:(1)∵AD∥BC,
∴∠ACF=∠DAC
∵∠AFC=∠DEA,AC=AD,
∴△ACF≌△DAE(AAS),
∴AF=DE;
(2)∵△ACF≌△DAE,
∴∠AFC=∠DEA,
∴∠AFB=∠DEC,
∵∠ABC=∠CDE,
∴△ABF∽△CDE,
∴=,
∴AF DE=BF CE,
∵AF=DE,
∴AF2=BF CE.
24.(2023秋 济阳区期末)2022年9月,教育部正式印发《义务教育课程方案》,《劳动教育》成为一门独立的课程,某学校率先行动,在校园开辟了一块劳动教育基地:一面利用学校的墙(墙的最大可用长度为15米),用长为30米的篱笆,围成矩形养殖园如图1,已知矩形的边CD靠院墙,AD和BC与院墙垂直,设AB的长为x m.
(1)当围成的矩形养殖园面积为100m2时,求BC的长;
(2)如图2,该学校打算在养殖园饲养鸡、鸭、鹅三种家禽,需要在中间多加上两道篱笆作为隔离网,并与院墙垂直,请问此时养殖园的面积能否达到100m2?若能,求出AB的长;若不能,请说明理由.
【解答】解:(1)设AB的长为x m,则矩形的宽BC=(30﹣x)m,
由题意得:x×(30﹣x)=100,
解得 x1=10,x2=20,
∵墙的最大可用长度为15米,
∴0<x≤15,
∴x=10,
即BC的长为10m;
(2)养殖园的面积不能达到100m2,理由如下:
假设养殖园的面积能达到100m2,设AB的长为y m,则BC的长为m,
根据题意得:y =100,
整理得:y2﹣30y+400=0,
∵Δ=(﹣30)2﹣4×1×400=﹣700<0,
∴原方程没有实数根,
∴假设不成立,即养殖园的面积不能达到100m2.
25.(2023秋 福州期末)某校后勤处每周周日均会对学校教室进行消毒处理,已知消毒水的消毒效果随着时间变化如图所示,消毒效果y(单位:效力)与时间x(单位:分钟)呈现三段函数图象,其中AB段是渐消毒阶段,BC段为深消毒阶段,CD段是反比例函数图象的一部分,为降消毒阶段.请根据图中信息解答下列问题:
(1)求深消毒阶段和降消毒阶段中y与x之间的函数关系式;
(2)若消毒效果持续28分钟达到4效力及以上,即可产生消毒作用,请问本次消毒是否有效?
【解答】解:(1)设BC段的函数解析式为y=kx+b,
把(10,3)和(30,6)代入得,
解得,
∴BC段的函数解析式为y=x+,
设CD段的函数解析式为y=,
把(30,6)代入得6=,
∴m=180,
∴CD段的函数解析式为y=;
(2)把y=4分别代入y=x+和y=得,
x=或x=45,
∵45﹣=28>28,
∴本次消毒有效.
26.(2022秋 源城区校级期末)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)若AE=4,AD=5,求AC的长.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC.
∵CF∥AE,
∴四边形AECF是平行四边形.
∵AE⊥BC,
∴∠AEC=90°,
∴平行四边形AECF是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=BC=5,OA=OC,AC⊥BD,
∵AE⊥BC,
∴∠AEB=90°,
∴,
∴CE=BE+BC=3+5=8,
∴.
27.(2023秋 金牛区期末)如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数的图象交于A,C两点,与x轴、y轴分别交于点B,D,已知点A的坐标为(﹣2,4),点C的坐标为(8,m).
(1)求一次函数和反比例函数的解析式;
(2)若点M在x轴上,以M、A、B为顶点的三角形与△BOD相似时,求点M的坐标;
(3)点P是直线AB下方反比例函数图象上一点,当△PAB的面积为24时,求点P的坐标.
【解答】解:(1)把点A(﹣2,4)代入得k=﹣2×4=﹣8,
∴反比例函数的解析式为y=﹣;
把(8,m)代入y=﹣得m=﹣=﹣1,
∴点C的坐标为(8,﹣1),
把A(﹣2,4)和点C(8,﹣1)代入,
解得,
∴一次函数的解析式为y=﹣x+3;
(2)设M(m,0),
在y=﹣x+3中,令x=0,则y=3,令y=0,则x=6,
∴D(0,3),B(6,0),
∴OD=3,OB=8,
∵以M、A、B为顶点的三角形与△BOD相似,
∴∠MAB=∠BOD=90°,
∴△ABM∽△DBO,
∴,
∵AM=,AB==4,BM=6﹣m,
∴=,
解得m=﹣4,m=0(不合题意舍去),
当∠AMB=∠BOD=90°,AM∥OD,
∴△AMB∽△DOB,
∴AM⊥x轴,
∴OM=2
即m=﹣2,
∴点M的坐标为(﹣4,0)或(﹣2,0);
(3)设点P的坐标为(n,﹣),
∵A(﹣2,4),B(6,0),
当点P在第四象限时,△PAB的面积=[6﹣(﹣2)]×[4﹣(﹣)]﹣×8×4﹣(4+)(n+2)﹣××(6﹣n)=24,
解得n=2,n=﹣8(不合题意舍去),
当点P在第二象限时,△PAB的面积=(4++4)(6﹣n)﹣×8×4﹣×(﹣2﹣n)(4+)=24,
解得n=﹣8,n=2(不合题意舍去)
综上所述,点P的坐标为(2,﹣4)或(﹣8,1).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
