2024-2025学年人教版七年级数学上册期末专题训练:与角度数相关的计算解答题(含解析)
文档属性
| 名称 | 2024-2025学年人教版七年级数学上册期末专题训练:与角度数相关的计算解答题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 09:02:42 | ||
图片预览

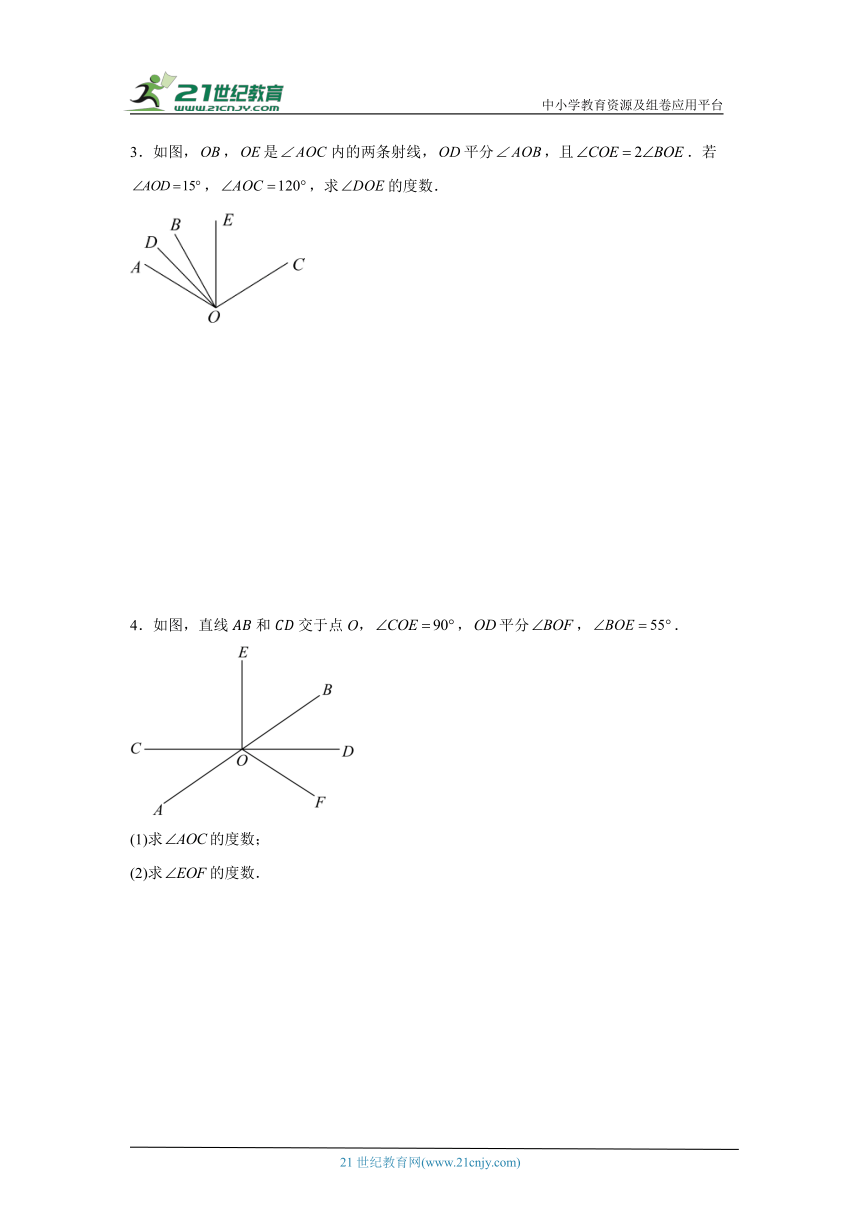
文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年人教版七年级数学上册期末专题训练:与角度数相关的计算解答题
1.如图,点A,O,B在同一条直线上,,分别平分和.
(1)求的度数;
(2)如果,求的度数.
2.如图,是的平分线,是的平分线,且,求:
(1)的度数;
(2)的度数.
3.如图,,是内的两条射线,平分,且.若,,求的度数.
4.如图,直线和交于点O,,平分,.
(1)求的度数;
(2)求的度数.
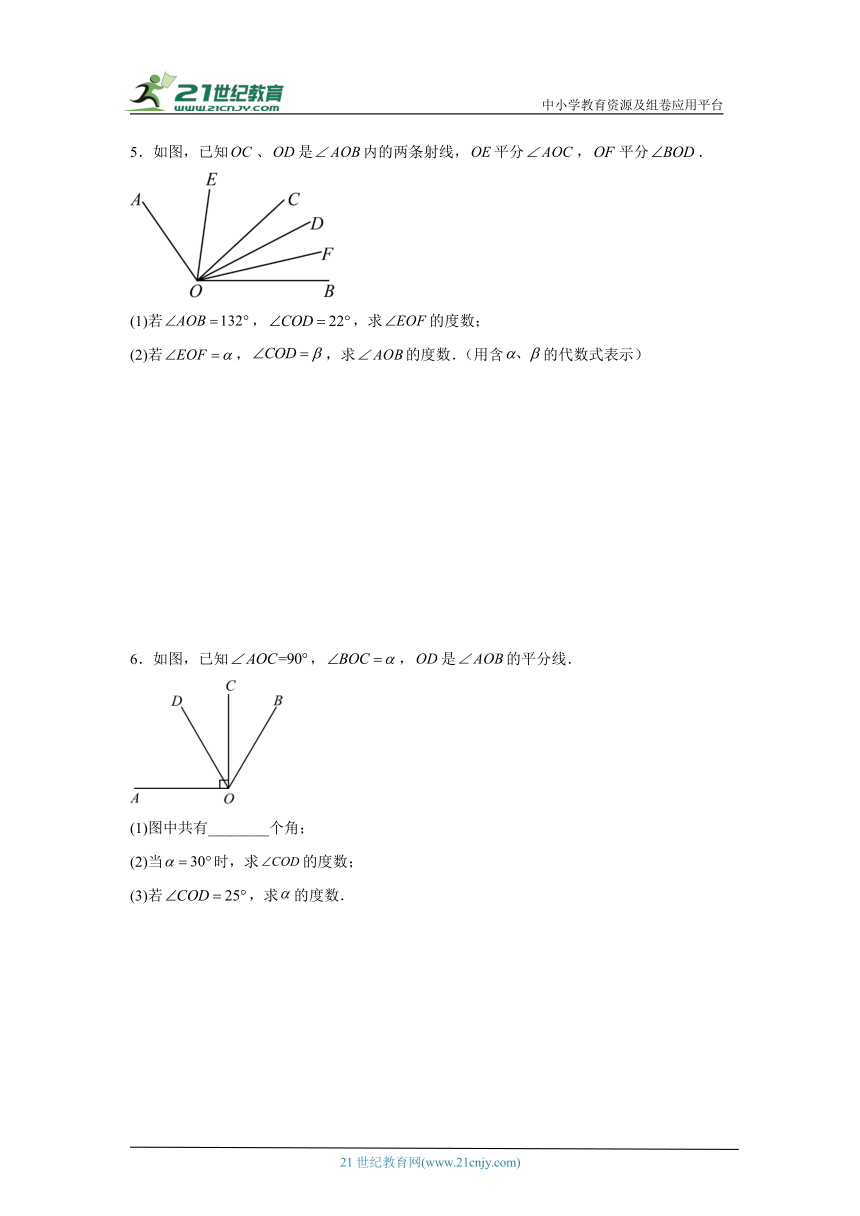
5.如图,已知、是内的两条射线,平分,平分.
(1)若,,求的度数;
(2)若,,求的度数.(用含的代数式表示)
6.如图,已知,,是的平分线.
(1)图中共有________个角;
(2)当时,求的度数;
(3)若,求的度数.
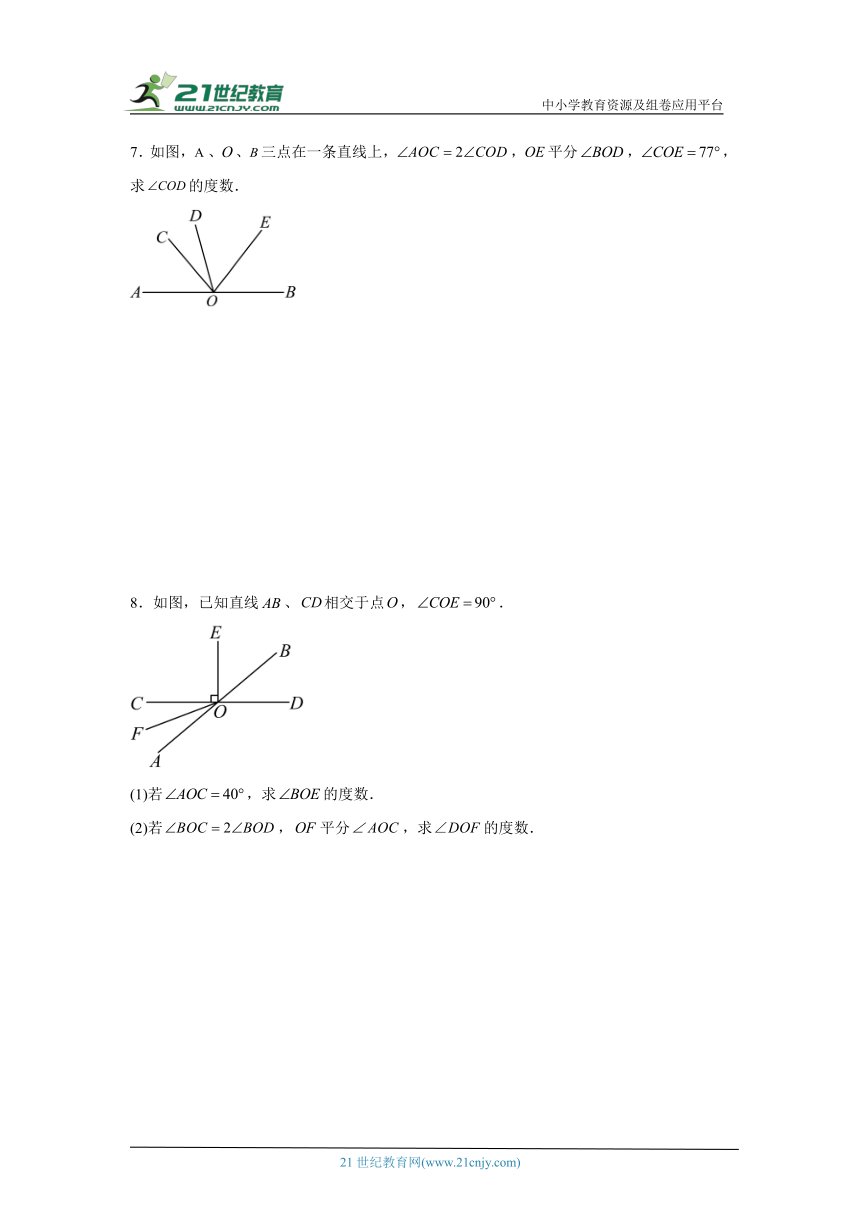
7.如图,、、三点在一条直线上,,平分,,求的度数.
8.如图,已知直线、相交于点,.
(1)若,求的度数.
(2)若,平分,求的度数.
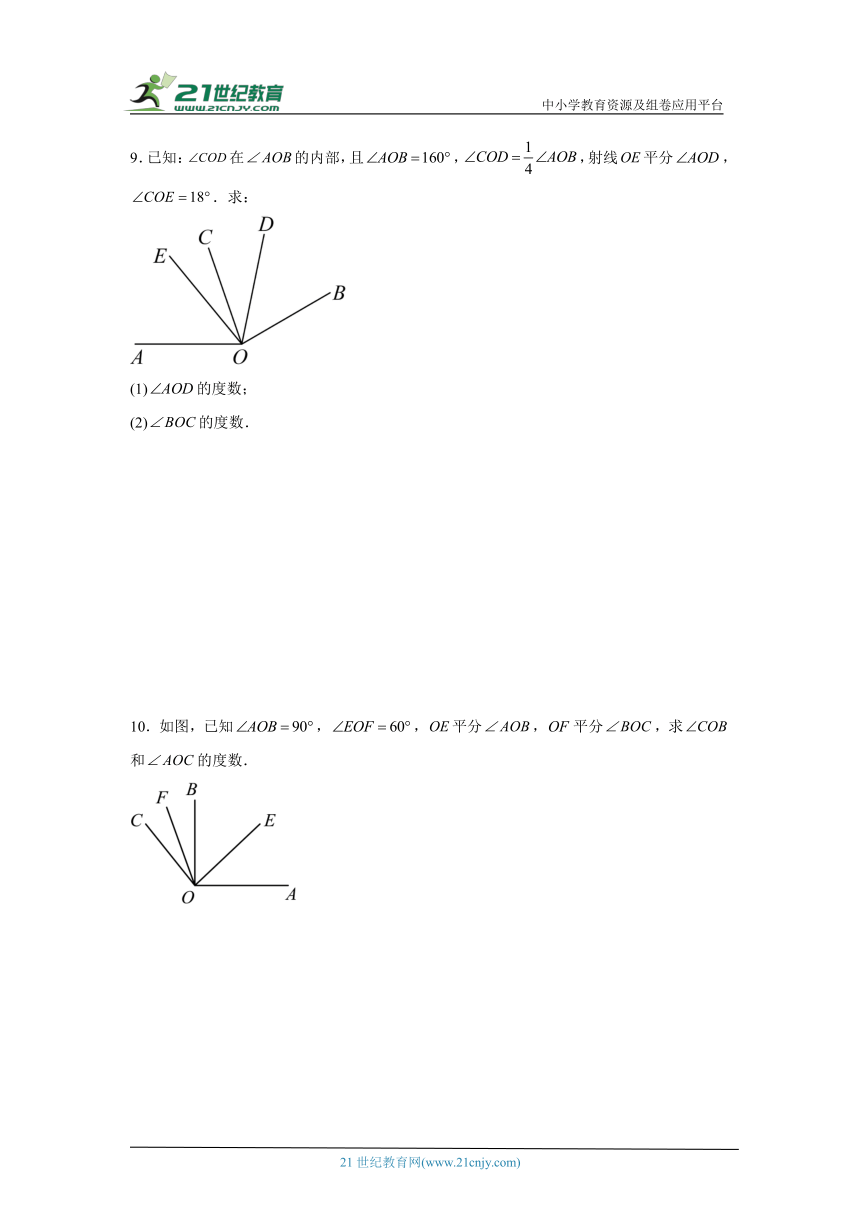
9.已知:在的内部,且,,射线平分,.求:
(1)的度数;
(2)的度数.
10.如图,已知,,平分,平分,求和的度数.
11.如图,是的平分线,是的平分线.
(1)如果,,那么是多少度?
(2)如果,,那么是多少度?
12.如图,是的平分线,是的平分线.
(1)若,求的度数;
(2)若,求的度数.
13.如图,已知,射线平分,射线平分.若,求的度数.
14.如图,平分,平分.若.
(1)求出的度数;
(2)判断与是否互补,并说明理由.
15.如图,点是直线上一点,平分,在直线另一侧以为顶点作.
(1)若,那么______;与的关系是______;与的关系是______;
(2)试说明与的关系成立的理由.
16.如图所示,点O是直线上一点,,平分.若,求的度数.
17.如图,O为直线上一点,平分.
(1)求出的度数;
(2)请通过计算说明是否平分.
18.如图,已知,,在内画射线,.
(1)如图1,求的度数;
(2)如图2,平分,平分,求的度数.
19.如图,为直线上一点,,是的角平分线,.
(1)图中小于平角的角有_______个;
(2)求的度数;
(3)猜想是否平分,并说明理由.
20.如图,点在直线上,射线与在直线的下方,射线与在直线的上方,且平分.
(1)若,求的度数;
(2)若平分,求的度数.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)
(2)
【分析】本题主要考查了角平分线的有关计算,以及角度的和差计算.
(1)利用平角的定义得出,再利用角平分线的定义可得出,,进而可得出.
(2)利用角平分线的定义,再根据角的和差关系即可得出,.
【详解】(1)解:∵点A,O,B在同一条直线上,
∴,
∵,分别平分和.
∴,,
∴,
即.
(2)∵,,平分,
∴,
∵
∴,
∴
2.(1)
(2)
【分析】本题考查几何图形中角度的计算,角平分线的定义,角的和差,
(1)根据角平分线的定义得,,代入数据计算即可;
(2)结合图形可得,代入数据计算即可;
解题的关键是掌握角平分线的定义:一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
【详解】(1)解:∵是的平分线,且,
∴,,
∵是的平分线,
∴,
∴的度数为;
(2)由(1)知:,,
∴,
∴的度数为.
3.
【分析】本题主要考查了角平分线的定义,几何图形中的角度计算.先根据角平分线的定义得出,,再根据,算出,根据,得出,根据求出结果即可.
【详解】解:∵平分,,
∴,,
∵,
∴,
∵,
又∵,
∴,
∴,
∴.
4.(1)
(2)
【分析】本题考查角的和差关系,角平分线有关的计算问题,运用数形结合思想解题是解题的关键.
(1)根据直接求解即可.
(2)利用求出,再运用平分得到,最后利用计算即可.
【详解】(1)解:因为,,,
所以;
(2)因为,,
所以,
因为平分,
所以,
所以.
5.(1)
(2)
【分析】本题主要考查了几何图形中角度的计算,角平分线的定义:
(1)先求出的度数,再由角平分线的定义推出的度数,据此根据角的和差关系可得答案;
(2)先求出的度数,再由角平分线的定义推出的度数,据此根据角的和差关系可得答案.
【详解】(1)解:∵,,
∴,
∵平分,平分,
∴,
∴,
∴.
(2)解:∵,,
∴,
∵平分,平分,
∴,
∴,
∴.
6.(1)6
(2)
(3)
【分析】本题主要考查了角平分线的定义,几何图形中角度的计算,角的个数问题:
(1)根据有公共顶点的两条射线可以确定一个角即可得到答案;
(2)先求出的度数,再由角平分线的定义求出的度数,据此可得答案;
(3)先求出的度数,再由角平分线的定义得到的度数,据此可得答案.
【详解】(1)解:图中有,共6个角,
故答案为:6;
(2)解:∵,
∴,
∵是的平分线,
∴,
∴;
(3)解:∵,
∴,
又∵是的平分线,,
∴,
∴,即.
7.
【分析】本题考查了角平分线的定义,平角的定义以及角度的和差计算问题的,解答本题的关键是方程思想的运用.
首先根据角平分线的概念得到,然后利用平角的概念求解即可.
【详解】解:因为平分,,
所以.
所以.
因为,,
所以,
所以.
8.(1)
(2)
【分析】本题主要考查互补、互余的定义,角平分线的定义,对顶角相等,理解图示,掌握角平分线的定义,几何中角度的和差计算即可求解.
(1)根据对顶角相等可得,根据互余的计算即可求解;
(2)根据补角的性质可得,由对顶角相等可得,根据角平分线的定义可得,再根据互补的定义即可求解.
【详解】(1)解:∵,,
∴,,
∴.
(2)解:∵,,
∴,
∴,
∵平分,
∴,
∴.
9.(1)
(2)
【分析】本题考查了角的计算和角平分线的定义,解题的关键是掌握角的和差计算和角平分线的定义.
(1)根据,可得,从而得到,然后根据角平分线的定义,即可求解;
(2)根据,,可得,即可求解.
【详解】(1)解:∵,,
∴,
∵,
∴,
∵射线平分,
∴;
(2)解:∵,,
∴,
∵
∴.
10.
【分析】本题主要考查了角平分线的定义,根据角的和差关系进行计算是解题的关键.先根据角平分线,求得的度数,再根据角的和差关系,求得的度数,最后根据角平分线,求得的度数.
【详解】,平分,
,
又,
,
平分,
,
.
11.(1)
(2)
【分析】本题考查角平分线,理解角平分线的定义以及图形中角的和差关系是解题的关键.
(1)根据角平分线的定义以及角的和差关系进行计算即可.
(2)根据角平分线的定义进行计算即可.
【详解】(1)解:∵是的平分线,是的平分线,,,
∴,,
∴.
(2)解:∵是的平分线,,
∴,
∵,
∴
∵是的平分线,
∴.
12.(1)
(2)
【分析】本题主要考查了角平分线的定义、角的和差运算等知识点,弄清角之间的关系成为解题的关键.
(1)由角平分线的定义可得,进而得到,再由角平分线的定义可得最后根据角的和差即可解答;
(2)由角平分线的定义可得,进而得到,再由角平分线的定义可得,最后根据角的和差即可解答.
【详解】(1)解:∵是的平分线,
∴,
∴.
∵是的平分线,
∴
∴.
(2)解:∵是的平分线,
∴,
∴.
∵OD是的平分线,
∴,
∴.
13.
【分析】本题主要考查了角平分线的定义、一元一次方程的定义等知识点,弄清楚各角之间的关系成为解题的关键.
设,由角平分线的定义可得,进而得到;再运用角平分线的定义可得,最后根据列一元一次方程求解即可.
【详解】解:设,
∵射线平分,
∴.
∵,
∴.
∵射线平分,
∴.
又∵,
∴,解得,即的度数为.
故答案为:.
14.(1)
(2)与互补.理由见解析
【分析】本题考查了角平分线有关计算,判断互补,解题的关键是熟练掌握角平分线定义,补角定义.
(1)利用角平分线的定义得出,结合,根据,代入计算即可;
(2)先利用角平分线的定义求出,,再根据,即可得答案.
【详解】(1)解:∵平分.,
∴,
∵,
∴;
(2)解:与互补.理由:
∵平分,平分,,
∴,,
∴,
∴,
故与互补.
15.(1),互余,互补
(2)理由见解析
【分析】题主要考查角平分线的定义,平角的定义,掌握角平分线和平角定义是解题的关键.
(1)先根据平角的意义,得,再由条件可知,由角平分线的定义得,根据得可求得答案;
(2)先证得,再利用平角的定义证得,即可证.
【详解】(1)解:∵点是直线上一点,
∴,
∵,
∴,
∴与互余,
∵,
∴,
∵平分,
∴
,
∴,
∴与互补;
故答案为:,互余,互补;
(2)∵点是直线上一点,平分,
∴,
∵,
∴,
∴,
即.
16.
【分析】本题考查角的计算,关键是掌握角平分线定义.由平角定义求出的度数,由角平分线定义求出的度数,即可求出的度数.
【详解】解:是直线上一点,
,
,
,
平分,
,
,
.
17.(1)
(2)平分,理由见解析
【分析】本题主要考查了角的度数的计算,正确理解角平分线的定义,以及邻补角的定义是解题的关键.
(1)根据,首先利用角平分线的定义和邻补角的定义求得和即可;
(2)根据与互余即可得出的度数,由(1)可知,那么,进而可得出结论,从而求解.
【详解】(1)解:,平分,
,
;
(2)平分.理由如下:
∵,
∴,
∵,
∴,
∴,
∴平分.
18.(1)
(2)
【分析】本题主要考查了角平分线性质等知识点,
(1)利用两个角的和进行计算即可;
(2)根据角平分线的意义和等式的性质,得出即可得解;
熟练掌握根据图形直观,得出角的和或差是解决此题的关键.
【详解】(1)
;
(2),
∴,
平分,
,
∵,
.
19.(1)9
(2)
(3)平分;理由见解析
【分析】此题考查角的计算问题,熟记平角的特点与角平分线的定义是解决此题的关键.
(1)根据角的数法进行解答即可;
(2)根据角平分线的定义得出,再利用互补解答即可;
(3)得出和的度数,再利用角平分线的定义解答即可.
【详解】(1)解:小于平角的角有,,,,,,,,共9个,
故答案为:9.
(2)∵为直线上一点,
∴;
∵,且是的平分线,
∴,
∴,
(3)平分.
理由如下:
∵,,
∴;
∵,,
∴,
∴,即平分.
20.(1)
(2)
【分析】本题考查了角平分线的定义,几何图形中角的计算,正确的识别图形是解题的关键;
(1)根据平分,得出,再根据,即可求解;
(2)设.根据平分表示出,得出,再根据平分,表示出,即可求解
【详解】(1)解:平分,
.
,
.
(2)解:设.
平分,
,
.
平分,
,
.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年人教版七年级数学上册期末专题训练:与角度数相关的计算解答题
1.如图,点A,O,B在同一条直线上,,分别平分和.
(1)求的度数;
(2)如果,求的度数.
2.如图,是的平分线,是的平分线,且,求:
(1)的度数;
(2)的度数.
3.如图,,是内的两条射线,平分,且.若,,求的度数.
4.如图,直线和交于点O,,平分,.
(1)求的度数;
(2)求的度数.
5.如图,已知、是内的两条射线,平分,平分.
(1)若,,求的度数;
(2)若,,求的度数.(用含的代数式表示)
6.如图,已知,,是的平分线.
(1)图中共有________个角;
(2)当时,求的度数;
(3)若,求的度数.
7.如图,、、三点在一条直线上,,平分,,求的度数.
8.如图,已知直线、相交于点,.
(1)若,求的度数.
(2)若,平分,求的度数.
9.已知:在的内部,且,,射线平分,.求:
(1)的度数;
(2)的度数.
10.如图,已知,,平分,平分,求和的度数.
11.如图,是的平分线,是的平分线.
(1)如果,,那么是多少度?
(2)如果,,那么是多少度?
12.如图,是的平分线,是的平分线.
(1)若,求的度数;
(2)若,求的度数.
13.如图,已知,射线平分,射线平分.若,求的度数.
14.如图,平分,平分.若.
(1)求出的度数;
(2)判断与是否互补,并说明理由.
15.如图,点是直线上一点,平分,在直线另一侧以为顶点作.
(1)若,那么______;与的关系是______;与的关系是______;
(2)试说明与的关系成立的理由.
16.如图所示,点O是直线上一点,,平分.若,求的度数.
17.如图,O为直线上一点,平分.
(1)求出的度数;
(2)请通过计算说明是否平分.
18.如图,已知,,在内画射线,.
(1)如图1,求的度数;
(2)如图2,平分,平分,求的度数.
19.如图,为直线上一点,,是的角平分线,.
(1)图中小于平角的角有_______个;
(2)求的度数;
(3)猜想是否平分,并说明理由.
20.如图,点在直线上,射线与在直线的下方,射线与在直线的上方,且平分.
(1)若,求的度数;
(2)若平分,求的度数.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)
(2)
【分析】本题主要考查了角平分线的有关计算,以及角度的和差计算.
(1)利用平角的定义得出,再利用角平分线的定义可得出,,进而可得出.
(2)利用角平分线的定义,再根据角的和差关系即可得出,.
【详解】(1)解:∵点A,O,B在同一条直线上,
∴,
∵,分别平分和.
∴,,
∴,
即.
(2)∵,,平分,
∴,
∵
∴,
∴
2.(1)
(2)
【分析】本题考查几何图形中角度的计算,角平分线的定义,角的和差,
(1)根据角平分线的定义得,,代入数据计算即可;
(2)结合图形可得,代入数据计算即可;
解题的关键是掌握角平分线的定义:一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
【详解】(1)解:∵是的平分线,且,
∴,,
∵是的平分线,
∴,
∴的度数为;
(2)由(1)知:,,
∴,
∴的度数为.
3.
【分析】本题主要考查了角平分线的定义,几何图形中的角度计算.先根据角平分线的定义得出,,再根据,算出,根据,得出,根据求出结果即可.
【详解】解:∵平分,,
∴,,
∵,
∴,
∵,
又∵,
∴,
∴,
∴.
4.(1)
(2)
【分析】本题考查角的和差关系,角平分线有关的计算问题,运用数形结合思想解题是解题的关键.
(1)根据直接求解即可.
(2)利用求出,再运用平分得到,最后利用计算即可.
【详解】(1)解:因为,,,
所以;
(2)因为,,
所以,
因为平分,
所以,
所以.
5.(1)
(2)
【分析】本题主要考查了几何图形中角度的计算,角平分线的定义:
(1)先求出的度数,再由角平分线的定义推出的度数,据此根据角的和差关系可得答案;
(2)先求出的度数,再由角平分线的定义推出的度数,据此根据角的和差关系可得答案.
【详解】(1)解:∵,,
∴,
∵平分,平分,
∴,
∴,
∴.
(2)解:∵,,
∴,
∵平分,平分,
∴,
∴,
∴.
6.(1)6
(2)
(3)
【分析】本题主要考查了角平分线的定义,几何图形中角度的计算,角的个数问题:
(1)根据有公共顶点的两条射线可以确定一个角即可得到答案;
(2)先求出的度数,再由角平分线的定义求出的度数,据此可得答案;
(3)先求出的度数,再由角平分线的定义得到的度数,据此可得答案.
【详解】(1)解:图中有,共6个角,
故答案为:6;
(2)解:∵,
∴,
∵是的平分线,
∴,
∴;
(3)解:∵,
∴,
又∵是的平分线,,
∴,
∴,即.
7.
【分析】本题考查了角平分线的定义,平角的定义以及角度的和差计算问题的,解答本题的关键是方程思想的运用.
首先根据角平分线的概念得到,然后利用平角的概念求解即可.
【详解】解:因为平分,,
所以.
所以.
因为,,
所以,
所以.
8.(1)
(2)
【分析】本题主要考查互补、互余的定义,角平分线的定义,对顶角相等,理解图示,掌握角平分线的定义,几何中角度的和差计算即可求解.
(1)根据对顶角相等可得,根据互余的计算即可求解;
(2)根据补角的性质可得,由对顶角相等可得,根据角平分线的定义可得,再根据互补的定义即可求解.
【详解】(1)解:∵,,
∴,,
∴.
(2)解:∵,,
∴,
∴,
∵平分,
∴,
∴.
9.(1)
(2)
【分析】本题考查了角的计算和角平分线的定义,解题的关键是掌握角的和差计算和角平分线的定义.
(1)根据,可得,从而得到,然后根据角平分线的定义,即可求解;
(2)根据,,可得,即可求解.
【详解】(1)解:∵,,
∴,
∵,
∴,
∵射线平分,
∴;
(2)解:∵,,
∴,
∵
∴.
10.
【分析】本题主要考查了角平分线的定义,根据角的和差关系进行计算是解题的关键.先根据角平分线,求得的度数,再根据角的和差关系,求得的度数,最后根据角平分线,求得的度数.
【详解】,平分,
,
又,
,
平分,
,
.
11.(1)
(2)
【分析】本题考查角平分线,理解角平分线的定义以及图形中角的和差关系是解题的关键.
(1)根据角平分线的定义以及角的和差关系进行计算即可.
(2)根据角平分线的定义进行计算即可.
【详解】(1)解:∵是的平分线,是的平分线,,,
∴,,
∴.
(2)解:∵是的平分线,,
∴,
∵,
∴
∵是的平分线,
∴.
12.(1)
(2)
【分析】本题主要考查了角平分线的定义、角的和差运算等知识点,弄清角之间的关系成为解题的关键.
(1)由角平分线的定义可得,进而得到,再由角平分线的定义可得最后根据角的和差即可解答;
(2)由角平分线的定义可得,进而得到,再由角平分线的定义可得,最后根据角的和差即可解答.
【详解】(1)解:∵是的平分线,
∴,
∴.
∵是的平分线,
∴
∴.
(2)解:∵是的平分线,
∴,
∴.
∵OD是的平分线,
∴,
∴.
13.
【分析】本题主要考查了角平分线的定义、一元一次方程的定义等知识点,弄清楚各角之间的关系成为解题的关键.
设,由角平分线的定义可得,进而得到;再运用角平分线的定义可得,最后根据列一元一次方程求解即可.
【详解】解:设,
∵射线平分,
∴.
∵,
∴.
∵射线平分,
∴.
又∵,
∴,解得,即的度数为.
故答案为:.
14.(1)
(2)与互补.理由见解析
【分析】本题考查了角平分线有关计算,判断互补,解题的关键是熟练掌握角平分线定义,补角定义.
(1)利用角平分线的定义得出,结合,根据,代入计算即可;
(2)先利用角平分线的定义求出,,再根据,即可得答案.
【详解】(1)解:∵平分.,
∴,
∵,
∴;
(2)解:与互补.理由:
∵平分,平分,,
∴,,
∴,
∴,
故与互补.
15.(1),互余,互补
(2)理由见解析
【分析】题主要考查角平分线的定义,平角的定义,掌握角平分线和平角定义是解题的关键.
(1)先根据平角的意义,得,再由条件可知,由角平分线的定义得,根据得可求得答案;
(2)先证得,再利用平角的定义证得,即可证.
【详解】(1)解:∵点是直线上一点,
∴,
∵,
∴,
∴与互余,
∵,
∴,
∵平分,
∴
,
∴,
∴与互补;
故答案为:,互余,互补;
(2)∵点是直线上一点,平分,
∴,
∵,
∴,
∴,
即.
16.
【分析】本题考查角的计算,关键是掌握角平分线定义.由平角定义求出的度数,由角平分线定义求出的度数,即可求出的度数.
【详解】解:是直线上一点,
,
,
,
平分,
,
,
.
17.(1)
(2)平分,理由见解析
【分析】本题主要考查了角的度数的计算,正确理解角平分线的定义,以及邻补角的定义是解题的关键.
(1)根据,首先利用角平分线的定义和邻补角的定义求得和即可;
(2)根据与互余即可得出的度数,由(1)可知,那么,进而可得出结论,从而求解.
【详解】(1)解:,平分,
,
;
(2)平分.理由如下:
∵,
∴,
∵,
∴,
∴,
∴平分.
18.(1)
(2)
【分析】本题主要考查了角平分线性质等知识点,
(1)利用两个角的和进行计算即可;
(2)根据角平分线的意义和等式的性质,得出即可得解;
熟练掌握根据图形直观,得出角的和或差是解决此题的关键.
【详解】(1)
;
(2),
∴,
平分,
,
∵,
.
19.(1)9
(2)
(3)平分;理由见解析
【分析】此题考查角的计算问题,熟记平角的特点与角平分线的定义是解决此题的关键.
(1)根据角的数法进行解答即可;
(2)根据角平分线的定义得出,再利用互补解答即可;
(3)得出和的度数,再利用角平分线的定义解答即可.
【详解】(1)解:小于平角的角有,,,,,,,,共9个,
故答案为:9.
(2)∵为直线上一点,
∴;
∵,且是的平分线,
∴,
∴,
(3)平分.
理由如下:
∵,,
∴;
∵,,
∴,
∴,即平分.
20.(1)
(2)
【分析】本题考查了角平分线的定义,几何图形中角的计算,正确的识别图形是解题的关键;
(1)根据平分,得出,再根据,即可求解;
(2)设.根据平分表示出,得出,再根据平分,表示出,即可求解
【详解】(1)解:平分,
.
,
.
(2)解:设.
平分,
,
.
平分,
,
.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
