2024-2025学年人教版七年级数学上册期末专题训练:整式加减的实际应用(含解析)
文档属性
| 名称 | 2024-2025学年人教版七年级数学上册期末专题训练:整式加减的实际应用(含解析) | 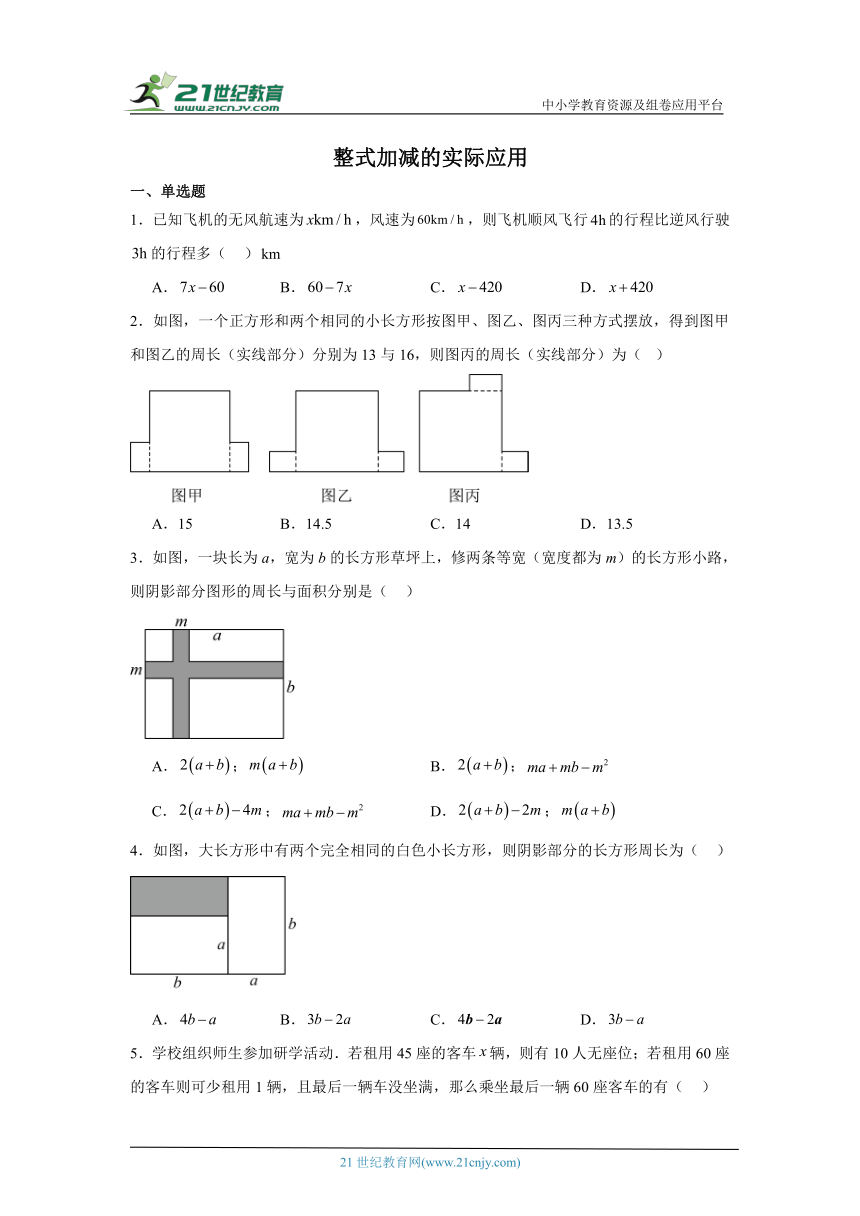 | |
| 格式 | docx | ||
| 文件大小 | 652.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 09:06:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
整式加减的实际应用
一、单选题
1.已知飞机的无风航速为,风速为,则飞机顺风飞行的行程比逆风行驶的行程多( )
A. B. C. D.
2.如图,一个正方形和两个相同的小长方形按图甲、图乙、图丙三种方式摆放,得到图甲和图乙的周长(实线部分)分别为13与16,则图丙的周长(实线部分)为( )
A.15 B.14.5 C.14 D.13.5
3.如图,一块长为a,宽为b的长方形草坪上,修两条等宽(宽度都为m)的长方形小路,则阴影部分图形的周长与面积分别是( )
A.; B.;
C.; D.;
4.如图,大长方形中有两个完全相同的白色小长方形,则阴影部分的长方形周长为( )
A. B. C. D.
5.学校组织师生参加研学活动.若租用45座的客车辆,则有10人无座位;若租用60座的客车则可少租用1辆,且最后一辆车没坐满,那么乘坐最后一辆60座客车的有( )
A.人 B.人 C.人 D.人
6.一个两位数的个位数字比十位数字小2,如果十位数字用a表示,那么这个两位数是( )
A. B. C. D.
7.某食品超市购进一种新口味饮料,每箱成本元,按每箱加价元后进行标价,然后面向消费者打出“八折”出售的销售方案,第一天销售了80箱,则这家超市第一天销售这80箱饮料所获利润为( )
A.元 B.元
C.元 D.元
8.若一个长方形的周长为,其中一边的长为,则与这一边相邻的另一边的长为( )
A. B. C. D.
9.已知一个两位数,它的十位数字是,个位数字是.将这个两位数的十位数字与个位数字交换位置后得到一个新的数,则所得数与原数的差(用含,的代数式表示)是( )
A. B. C. D.
10.将8张长为,宽为的小长方形纸片,按图1和图2所示的两种方式放在长方形内(相邻的小长方形既无重叠,又不留空隙).图1中两块阴影部分的周长和为,图2中阴影部分的周长为.若长方形的长比宽大,则的值为( )
A. B. C. D.
二、填空题
11.若长方形的一边长是,另一边长为,则这个长方形的周长为 .
12.小王今年a岁,小刘今年岁,再过5年他们相差 岁.
13.长方形的周长为,长为,则宽为 .
14.某4名工人3月份完成的总工作量比此月人均定额的4倍多12件,如果设此月人均定额是x件,那么这4名工人此月实际人均工作量为 件.(用含x的式子表示)
15.长方形的长为,宽为,把长减少,宽增加后,所得的长方形面积比原来长方形面积大 .
16.把2张大小形状完全相同的平行四边形纸片(如图1)按两种不同的方式(如图2、图3)不重叠地放在平行四边形内,未被覆盖的部分用阴影表示,若,,则图3中阴影部分的周长与图2中阴影部分的周长的差值为 .
17.某牧民共有牛羊120只,每只牛每天的食草量是羊的4倍,若每只羊每天需要4千克草,设牛有只,该牧民每天需准备 千克草.
18.某学校计划购买甲、乙两种品牌的电子白板共20台.甲、乙两种品牌电子白板的单价分别为3万元/台和2万元/台.若购买甲品牌电子白板费用为万元,则购买乙品牌电子白板费用为 万元.(用含x的代数式表示)
19.三个小队植树,第一队种棵,第二队种的树比第一队种的树的2倍还多4棵,第三队种的树比第二队种的树的一半少6棵,三队共种树 棵.
20.如图,已知小正方形的边长为a,大正方形的边长为6,则图中阴影部分面积为 .(用含a的式子表示)
三、解答题
21.如图是某居民小区的一块长为米,宽为米的长方形空地,为了美化环境,准备在这个长方形空地的四个顶点处修建一个半径为米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花的费用为每平方米100元,种草的费用为每平方米50元.
(1)求美化这块空地共需多少元?(用含有,,的式子表示)
(2)当,,时,美化这块空地共需多少元?
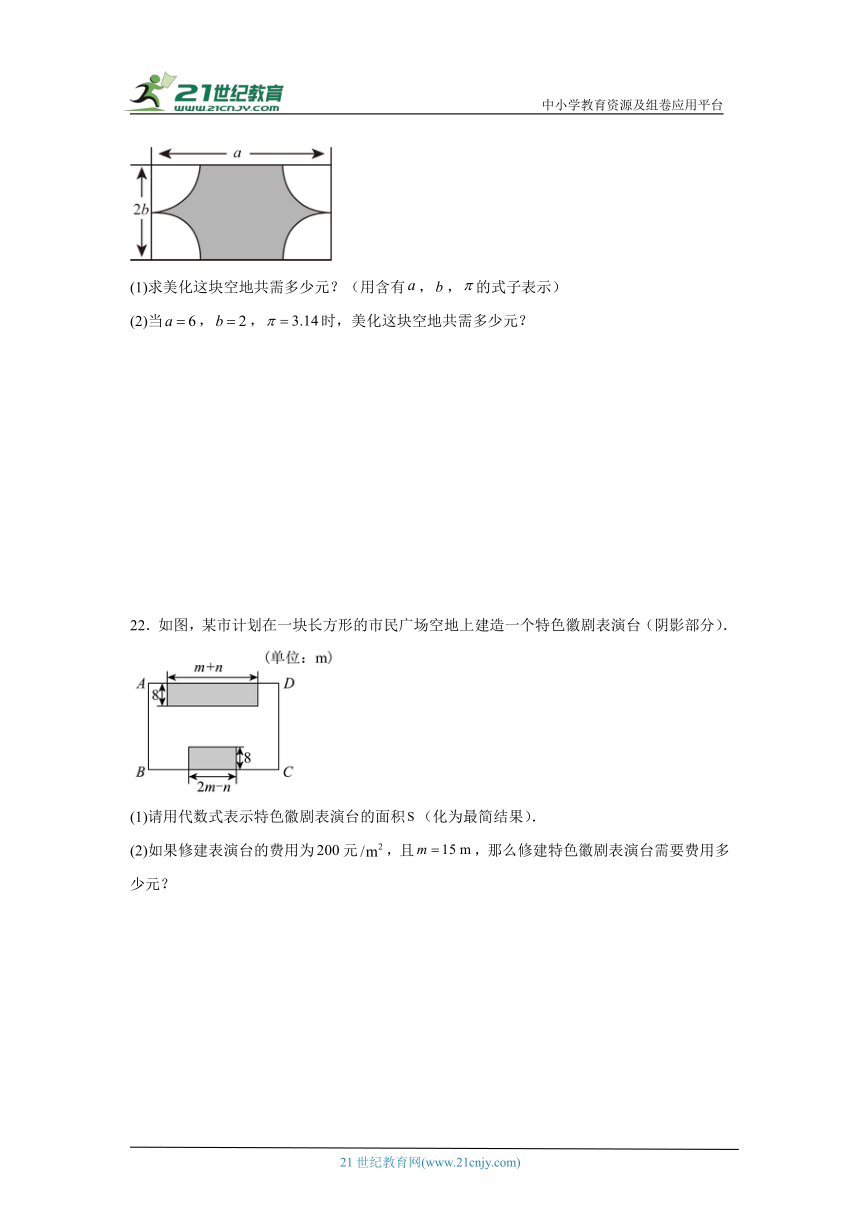
22.如图,某市计划在一块长方形的市民广场空地上建造一个特色徽剧表演台(阴影部分).
(1)请用代数式表示特色徽剧表演台的面积(化为最简结果).
(2)如果修建表演台的费用为元,且,那么修建特色徽剧表演台需要费用多少元?
23.窗户的形状如图所示(图中长度单位:,其上部为半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长为.计算:
(1)窗户的面积是多少?
(2)窗户的外框的总长是多少?
(3)当时,窗户的面积和外框的总长分别是多少?
24.初一4班将买一些乒乓球和乒乓球拍,现了解情况如下:
甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每幅定价30元,乒乓球每盒定价5元,经洽谈后,甲店买一副球拍送一盒乒乓球,乙店全按定价的9折优惠.该班需球拍5副,乒乓球x盒().(注:打9折即为原价×0.9)
(1)请你用x的代数式分别表示在甲、乙两商店的付款费用;
(2)购买15盒乒乓球时,去哪家商店买更便宜?若购买25盒乒乓球,哪家更便宜?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B C B D A B D B
1.D
【分析】本题考查了列代数式,熟练掌握风速、航速、时间和行程的关系是解题的关键.根据飞机顺风航速无风航速风速,飞机逆风航速无风航速风速,由飞机顺风飞行,逆风行驶,列出代数式计算即可.
【详解】解:∵飞机顺风航速无风航速风速,飞机逆风航速无风航速风速,
∴飞机顺风飞行的行程比逆风行驶的行程多:,
故选:D.
2.B
【分析】本题考查列代数式,整体思想的巧妙运用是解题的关键.分别设正方形的边长为a,小长方形的长为b,宽为c,根据图甲和图乙的周长得出a,b,c之间的关系即可解决问题.
【详解】解:设正方形的边长为,小长方形的长为,宽为,
则图甲的周长可表示为:,
所以①;
图乙的周长可表示为:,
所以②;
图丙的周长可表示为:.
将①②两式相加再除以2得,
,
即,
所以图丙的周长为14.5.
故选:B.
3.B
【分析】本题考查了几何图形的周长、面积问题、列代数式表示式等知识,根据图形结合长方形的周长与面积的公式列出代数式即可得出答案,正确列出代数式并进行简单计算是解题的关键.
【详解】解:阴影部分图形为两个宽都为长方形,一个长方形的长为,另一个长方形的长为,两个长方形重合部分为一个边长为的正方形,
则周长为,
面积为,
故选:.
4.C
【分析】本题考查了列代数式,利用长方形的性质得到阴影部分长方形的长为,宽为,然后计算它的周长.
【详解】解:阴影部分长方形的长为,宽为,
所以阴影部分长方形的周长.
故选:C.
5.B
【分析】本题考查列代数式.用总人数减去前面车上的人数求出最后一辆车上的人数即可.读懂题意,正确的列出代数式,是解题的关键.
【详解】解:租用45座的客车辆,则有10人无座位,
∴总人数为:人,
∴乘坐最后一辆60座客车的有人;
故选B.
6.D
【分析】本题主要考查列代数式和整式的加减,解题的关键是熟练掌握两位数的表示方法.
根据数字的表示方法表示出这个两位数,然后化简即可.
【详解】解:∵一个两位数的个位数字比十位数字小2,如果十位数字用a表示,
∴个位数字为,
∴这个两位数为.
故选:D.
7.A
【分析】本题考查了整式加减的应用,根据实际售价减去成本列式计算即可.
【详解】这这家超市第一天销售这80箱饮料所获利润为(元);
故选:A.
8.B
【分析】本题主要考查了整式加减的应用.根据题意可得与这一边相邻的另一边的长为,再直接利用去括号、合并同类项法则得出答案.
【详解】解:根据题意得:与这一边相邻的另一边的长为
.
故选:B
9.D
【分析】本题考查了列代数式以及整式的加减混合运算:先表示原两位数为,再表示交换位置后的两位数为,再根据“所得数与原数的差”进行列式计算,即可作答.
【详解】解:∵一个两位数,它的十位数字是,个位数字是.
∴原两位数为
∵将这个两位数的十位数字与个位数字交换位置后得到一个新的数,
∴交换位置后的两位数为
则
故选:D
10.B
【分析】本题考查的是整式的加减.将图1拆成两个长方形,计算出长方形的宽为,再求得长方形的长为;根据平移的性质,将转化为,据此计算即可得出答案.
【详解】解:将图1拆成两个长方形,可知,宽为,
则长为,
根据平移的性质知,
的值为.
故选:B.
11.
【分析】此题考查了整式的加减运算,长方形的周长等于两邻边之和的2倍,表示出周长,去括号合并即可得到结果.
【详解】根据题意列得:,
则这个长方形的周长为.
故答案为:.
12.3
【分析】本题考查整式的加减,解答本题的关键是明确题意,列出相应的代数式.求得过5年后他们的年龄,相减即可得出他们的年龄差.
【详解】解:,
故答案为:3.
13./
【分析】本题考查整式加减的应用.根据长方形的周长公式列出相应的代数式计算即可求解.
【详解】解:长方形的宽为,
故答案为:.
14.
【分析】考查了列代数式,整式加减的应用.列代数式的关键是正确理解文字语言中的关键词,比如该题中的“倍”、“和”等,从而明确其中的运算关系,正确地列出代数式.
根据4名工人3月份完成的总工作量比此月人均定额的4倍多12件得到总工作量是件,再把总工作量乘以可得这4名工人此月实际人均工作量.
【详解】解:(件).
答:这4名工人此月实际人均工作量为件.
故答案为:
15./
【分析】本题考查了对整式的加减的连接和掌握,根据题意分别算出原来长方形的面积,所得长方形的面积为,相减即可得;根据题意正确计算初代数式是解题的关键.
【详解】解:原来长方形的面积为:,
所得长方形的面积为:,
则得的长方形面积比原来长方形面积大:,
故答案为:.
16.2
【分析】本题考查了列代数式以及整式的加减混合运算,设小平行四边形的长边为,短边为,由题意得,,分别得出,,计算差值即可求解.解题关键是弄清题意,找出合适的数量关系,列出代数式,在解题时要根据题意结合图形得出答案.
【详解】设小平行四边形的长边为,短边为,由题意得:,,
如图2,
,
如图3,
,
∴.
故答案为:.
17.
【分析】本题考查了列方程,关键是根据等量关系列方程.
根据设牛有只,则羊有,再根据每只牛每天的食草量是羊的4倍,每只羊每天需要4千克草,列方程即可解答.
【详解】解:设牛有只,则羊有只,
∵每只牛每天的食草量是羊的4倍,若每只羊每天需要4千克草,
∴牧民每天需准备:千克草.
故答案为:.
18.
【分析】本题考查了列代数式,根据各数量之间的关系,找出购买乙品牌电子白板的数量是解题的关键.
利用数量=总价÷单价,可找出购买甲品牌电子白板的数量,结合购买甲、乙两种品牌电子白板的总数量,可得出购买乙品牌电子白板的数量,再利用总价=单价×数量,即可得出购买乙品牌电子白板的总费用.
【详解】解:∵甲品牌电子白板的单价为3万元/台,购买甲品牌电子白板费用为万元,
∴购买甲品牌电子白板台,
∵该学校计划购买甲、乙两种品牌的电子白板共20台,
∴购买乙品牌电子白板台,
又∵乙品牌电子白板的单价为2万元/台,
∴购买乙品牌电子白板费用为万元.
故答案为:.
19.
【分析】本题考查整式的加减,先列式表示第二队种的树的数量,再列式表示第三队种的树的棵数,最后求和是解题的关键.
【详解】解:依题意得:第二队树的数量为棵, 第三队种的树的棵树为棵,
所以三队共种树(棵),
故答案为:.
20.
【分析】本题主要考查了求阴影部分面积,以及用代数式表示式,根据阴影部分面积等于两个正方形的面积减去两个白色三角形的面积计算即可.
【详解】解:根据题意:
两个正方形的面积之和为:,
一个小白三角形和一个大白三角形的面积之和为:,
∴阴影部分面积为:.
故答案为:.
21.(1)元
(2)1828元
【分析】此题考查了代数式求值在几何图形问题中的应用,熟练掌握矩形和扇形面积公式,代数式求值,是解题的关键.
(1)四个花台的面积为一个圆的面积,种草部分的面积为长方形的面积减去四个花台的面积,总费用为相应的单价乘以面积,然后求和即可;
(2)将,,代入(1)中所得的代数式,计算即可.
【详解】(1)解:由题意,得花台面积为,
∴其余部分的面积为:,
∴美化这块空地共需费用:
(元).
故美化这块空地共需元;
(2)解:将,,代入(1)中所得的代数式得:(元).
故美化这块空地共需1828元.
22.(1)
(2)72000元
【分析】本题考查列代数式、代数式求值以及整式的加减,解题的关键是明确题意,列出相应的代数式,会求代数式的值.
(1)根据图形列出算式,再进一步化简求解即可;
(2)先根据化简后的代数式求出表演台的面积,再乘以单价即可得出答案.
【详解】(1)解:特色徽剧表演台的面积
.
(2)解:当时,
,
所以修建特色徽剧表演台需要费用(元).
23.(1)
(2)
(3)窗户的面积是,窗户的外框的总长是:
【分析】(1)窗户的面积等于四个小正方形的面积与半圆的面积之和即可得;
(2)大正方形的三条边长加上圆的周长的一半即可得;
(3)把代入(1)(2)中所列代数式求值即可.
本题考查了整式加法的应用及化简求值,熟练掌握正方形与圆的周长和面积公式是解题关键.
【详解】(1)窗户的面积是:;
(2)窗户的外框的总长是:;
(3)当时,窗户的面积是:
窗户的外框的总长是:.
24.(1)()元,()元
(2)乙商店,见解析
【分析】本题考查列代数式解决实际问题.根据题意正确的列出代数式是解题的关键.
(1)根据题意,列出代数式即可;
(2)将时代入两个代数式进行求值,再将时代入两个代数式进行求值,通过比较数值的大小即可得解.
【详解】(1)解:甲商店的付款费用为:(元)
乙商店的付款费用为:(元)
(2)解:当时:
去甲商店的付款费用为:元;
去乙商店的付款费用为:元;
∵,
∴去甲商店购买;
当时:
去甲商店的付款费用为:元;
去乙商店的付款费用为:元;
∵,
∴去乙商店购买;
∴购买15盒乒乓球时,到甲商店购买更便宜;购买25盒乒乓球时,到乙商店购买更便宜.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
整式加减的实际应用
一、单选题
1.已知飞机的无风航速为,风速为,则飞机顺风飞行的行程比逆风行驶的行程多( )
A. B. C. D.
2.如图,一个正方形和两个相同的小长方形按图甲、图乙、图丙三种方式摆放,得到图甲和图乙的周长(实线部分)分别为13与16,则图丙的周长(实线部分)为( )
A.15 B.14.5 C.14 D.13.5
3.如图,一块长为a,宽为b的长方形草坪上,修两条等宽(宽度都为m)的长方形小路,则阴影部分图形的周长与面积分别是( )
A.; B.;
C.; D.;
4.如图,大长方形中有两个完全相同的白色小长方形,则阴影部分的长方形周长为( )
A. B. C. D.
5.学校组织师生参加研学活动.若租用45座的客车辆,则有10人无座位;若租用60座的客车则可少租用1辆,且最后一辆车没坐满,那么乘坐最后一辆60座客车的有( )
A.人 B.人 C.人 D.人
6.一个两位数的个位数字比十位数字小2,如果十位数字用a表示,那么这个两位数是( )
A. B. C. D.
7.某食品超市购进一种新口味饮料,每箱成本元,按每箱加价元后进行标价,然后面向消费者打出“八折”出售的销售方案,第一天销售了80箱,则这家超市第一天销售这80箱饮料所获利润为( )
A.元 B.元
C.元 D.元
8.若一个长方形的周长为,其中一边的长为,则与这一边相邻的另一边的长为( )
A. B. C. D.
9.已知一个两位数,它的十位数字是,个位数字是.将这个两位数的十位数字与个位数字交换位置后得到一个新的数,则所得数与原数的差(用含,的代数式表示)是( )
A. B. C. D.
10.将8张长为,宽为的小长方形纸片,按图1和图2所示的两种方式放在长方形内(相邻的小长方形既无重叠,又不留空隙).图1中两块阴影部分的周长和为,图2中阴影部分的周长为.若长方形的长比宽大,则的值为( )
A. B. C. D.
二、填空题
11.若长方形的一边长是,另一边长为,则这个长方形的周长为 .
12.小王今年a岁,小刘今年岁,再过5年他们相差 岁.
13.长方形的周长为,长为,则宽为 .
14.某4名工人3月份完成的总工作量比此月人均定额的4倍多12件,如果设此月人均定额是x件,那么这4名工人此月实际人均工作量为 件.(用含x的式子表示)
15.长方形的长为,宽为,把长减少,宽增加后,所得的长方形面积比原来长方形面积大 .
16.把2张大小形状完全相同的平行四边形纸片(如图1)按两种不同的方式(如图2、图3)不重叠地放在平行四边形内,未被覆盖的部分用阴影表示,若,,则图3中阴影部分的周长与图2中阴影部分的周长的差值为 .
17.某牧民共有牛羊120只,每只牛每天的食草量是羊的4倍,若每只羊每天需要4千克草,设牛有只,该牧民每天需准备 千克草.
18.某学校计划购买甲、乙两种品牌的电子白板共20台.甲、乙两种品牌电子白板的单价分别为3万元/台和2万元/台.若购买甲品牌电子白板费用为万元,则购买乙品牌电子白板费用为 万元.(用含x的代数式表示)
19.三个小队植树,第一队种棵,第二队种的树比第一队种的树的2倍还多4棵,第三队种的树比第二队种的树的一半少6棵,三队共种树 棵.
20.如图,已知小正方形的边长为a,大正方形的边长为6,则图中阴影部分面积为 .(用含a的式子表示)
三、解答题
21.如图是某居民小区的一块长为米,宽为米的长方形空地,为了美化环境,准备在这个长方形空地的四个顶点处修建一个半径为米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花的费用为每平方米100元,种草的费用为每平方米50元.
(1)求美化这块空地共需多少元?(用含有,,的式子表示)
(2)当,,时,美化这块空地共需多少元?
22.如图,某市计划在一块长方形的市民广场空地上建造一个特色徽剧表演台(阴影部分).
(1)请用代数式表示特色徽剧表演台的面积(化为最简结果).
(2)如果修建表演台的费用为元,且,那么修建特色徽剧表演台需要费用多少元?
23.窗户的形状如图所示(图中长度单位:,其上部为半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长为.计算:
(1)窗户的面积是多少?
(2)窗户的外框的总长是多少?
(3)当时,窗户的面积和外框的总长分别是多少?
24.初一4班将买一些乒乓球和乒乓球拍,现了解情况如下:
甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每幅定价30元,乒乓球每盒定价5元,经洽谈后,甲店买一副球拍送一盒乒乓球,乙店全按定价的9折优惠.该班需球拍5副,乒乓球x盒().(注:打9折即为原价×0.9)
(1)请你用x的代数式分别表示在甲、乙两商店的付款费用;
(2)购买15盒乒乓球时,去哪家商店买更便宜?若购买25盒乒乓球,哪家更便宜?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B C B D A B D B
1.D
【分析】本题考查了列代数式,熟练掌握风速、航速、时间和行程的关系是解题的关键.根据飞机顺风航速无风航速风速,飞机逆风航速无风航速风速,由飞机顺风飞行,逆风行驶,列出代数式计算即可.
【详解】解:∵飞机顺风航速无风航速风速,飞机逆风航速无风航速风速,
∴飞机顺风飞行的行程比逆风行驶的行程多:,
故选:D.
2.B
【分析】本题考查列代数式,整体思想的巧妙运用是解题的关键.分别设正方形的边长为a,小长方形的长为b,宽为c,根据图甲和图乙的周长得出a,b,c之间的关系即可解决问题.
【详解】解:设正方形的边长为,小长方形的长为,宽为,
则图甲的周长可表示为:,
所以①;
图乙的周长可表示为:,
所以②;
图丙的周长可表示为:.
将①②两式相加再除以2得,
,
即,
所以图丙的周长为14.5.
故选:B.
3.B
【分析】本题考查了几何图形的周长、面积问题、列代数式表示式等知识,根据图形结合长方形的周长与面积的公式列出代数式即可得出答案,正确列出代数式并进行简单计算是解题的关键.
【详解】解:阴影部分图形为两个宽都为长方形,一个长方形的长为,另一个长方形的长为,两个长方形重合部分为一个边长为的正方形,
则周长为,
面积为,
故选:.
4.C
【分析】本题考查了列代数式,利用长方形的性质得到阴影部分长方形的长为,宽为,然后计算它的周长.
【详解】解:阴影部分长方形的长为,宽为,
所以阴影部分长方形的周长.
故选:C.
5.B
【分析】本题考查列代数式.用总人数减去前面车上的人数求出最后一辆车上的人数即可.读懂题意,正确的列出代数式,是解题的关键.
【详解】解:租用45座的客车辆,则有10人无座位,
∴总人数为:人,
∴乘坐最后一辆60座客车的有人;
故选B.
6.D
【分析】本题主要考查列代数式和整式的加减,解题的关键是熟练掌握两位数的表示方法.
根据数字的表示方法表示出这个两位数,然后化简即可.
【详解】解:∵一个两位数的个位数字比十位数字小2,如果十位数字用a表示,
∴个位数字为,
∴这个两位数为.
故选:D.
7.A
【分析】本题考查了整式加减的应用,根据实际售价减去成本列式计算即可.
【详解】这这家超市第一天销售这80箱饮料所获利润为(元);
故选:A.
8.B
【分析】本题主要考查了整式加减的应用.根据题意可得与这一边相邻的另一边的长为,再直接利用去括号、合并同类项法则得出答案.
【详解】解:根据题意得:与这一边相邻的另一边的长为
.
故选:B
9.D
【分析】本题考查了列代数式以及整式的加减混合运算:先表示原两位数为,再表示交换位置后的两位数为,再根据“所得数与原数的差”进行列式计算,即可作答.
【详解】解:∵一个两位数,它的十位数字是,个位数字是.
∴原两位数为
∵将这个两位数的十位数字与个位数字交换位置后得到一个新的数,
∴交换位置后的两位数为
则
故选:D
10.B
【分析】本题考查的是整式的加减.将图1拆成两个长方形,计算出长方形的宽为,再求得长方形的长为;根据平移的性质,将转化为,据此计算即可得出答案.
【详解】解:将图1拆成两个长方形,可知,宽为,
则长为,
根据平移的性质知,
的值为.
故选:B.
11.
【分析】此题考查了整式的加减运算,长方形的周长等于两邻边之和的2倍,表示出周长,去括号合并即可得到结果.
【详解】根据题意列得:,
则这个长方形的周长为.
故答案为:.
12.3
【分析】本题考查整式的加减,解答本题的关键是明确题意,列出相应的代数式.求得过5年后他们的年龄,相减即可得出他们的年龄差.
【详解】解:,
故答案为:3.
13./
【分析】本题考查整式加减的应用.根据长方形的周长公式列出相应的代数式计算即可求解.
【详解】解:长方形的宽为,
故答案为:.
14.
【分析】考查了列代数式,整式加减的应用.列代数式的关键是正确理解文字语言中的关键词,比如该题中的“倍”、“和”等,从而明确其中的运算关系,正确地列出代数式.
根据4名工人3月份完成的总工作量比此月人均定额的4倍多12件得到总工作量是件,再把总工作量乘以可得这4名工人此月实际人均工作量.
【详解】解:(件).
答:这4名工人此月实际人均工作量为件.
故答案为:
15./
【分析】本题考查了对整式的加减的连接和掌握,根据题意分别算出原来长方形的面积,所得长方形的面积为,相减即可得;根据题意正确计算初代数式是解题的关键.
【详解】解:原来长方形的面积为:,
所得长方形的面积为:,
则得的长方形面积比原来长方形面积大:,
故答案为:.
16.2
【分析】本题考查了列代数式以及整式的加减混合运算,设小平行四边形的长边为,短边为,由题意得,,分别得出,,计算差值即可求解.解题关键是弄清题意,找出合适的数量关系,列出代数式,在解题时要根据题意结合图形得出答案.
【详解】设小平行四边形的长边为,短边为,由题意得:,,
如图2,
,
如图3,
,
∴.
故答案为:.
17.
【分析】本题考查了列方程,关键是根据等量关系列方程.
根据设牛有只,则羊有,再根据每只牛每天的食草量是羊的4倍,每只羊每天需要4千克草,列方程即可解答.
【详解】解:设牛有只,则羊有只,
∵每只牛每天的食草量是羊的4倍,若每只羊每天需要4千克草,
∴牧民每天需准备:千克草.
故答案为:.
18.
【分析】本题考查了列代数式,根据各数量之间的关系,找出购买乙品牌电子白板的数量是解题的关键.
利用数量=总价÷单价,可找出购买甲品牌电子白板的数量,结合购买甲、乙两种品牌电子白板的总数量,可得出购买乙品牌电子白板的数量,再利用总价=单价×数量,即可得出购买乙品牌电子白板的总费用.
【详解】解:∵甲品牌电子白板的单价为3万元/台,购买甲品牌电子白板费用为万元,
∴购买甲品牌电子白板台,
∵该学校计划购买甲、乙两种品牌的电子白板共20台,
∴购买乙品牌电子白板台,
又∵乙品牌电子白板的单价为2万元/台,
∴购买乙品牌电子白板费用为万元.
故答案为:.
19.
【分析】本题考查整式的加减,先列式表示第二队种的树的数量,再列式表示第三队种的树的棵数,最后求和是解题的关键.
【详解】解:依题意得:第二队树的数量为棵, 第三队种的树的棵树为棵,
所以三队共种树(棵),
故答案为:.
20.
【分析】本题主要考查了求阴影部分面积,以及用代数式表示式,根据阴影部分面积等于两个正方形的面积减去两个白色三角形的面积计算即可.
【详解】解:根据题意:
两个正方形的面积之和为:,
一个小白三角形和一个大白三角形的面积之和为:,
∴阴影部分面积为:.
故答案为:.
21.(1)元
(2)1828元
【分析】此题考查了代数式求值在几何图形问题中的应用,熟练掌握矩形和扇形面积公式,代数式求值,是解题的关键.
(1)四个花台的面积为一个圆的面积,种草部分的面积为长方形的面积减去四个花台的面积,总费用为相应的单价乘以面积,然后求和即可;
(2)将,,代入(1)中所得的代数式,计算即可.
【详解】(1)解:由题意,得花台面积为,
∴其余部分的面积为:,
∴美化这块空地共需费用:
(元).
故美化这块空地共需元;
(2)解:将,,代入(1)中所得的代数式得:(元).
故美化这块空地共需1828元.
22.(1)
(2)72000元
【分析】本题考查列代数式、代数式求值以及整式的加减,解题的关键是明确题意,列出相应的代数式,会求代数式的值.
(1)根据图形列出算式,再进一步化简求解即可;
(2)先根据化简后的代数式求出表演台的面积,再乘以单价即可得出答案.
【详解】(1)解:特色徽剧表演台的面积
.
(2)解:当时,
,
所以修建特色徽剧表演台需要费用(元).
23.(1)
(2)
(3)窗户的面积是,窗户的外框的总长是:
【分析】(1)窗户的面积等于四个小正方形的面积与半圆的面积之和即可得;
(2)大正方形的三条边长加上圆的周长的一半即可得;
(3)把代入(1)(2)中所列代数式求值即可.
本题考查了整式加法的应用及化简求值,熟练掌握正方形与圆的周长和面积公式是解题关键.
【详解】(1)窗户的面积是:;
(2)窗户的外框的总长是:;
(3)当时,窗户的面积是:
窗户的外框的总长是:.
24.(1)()元,()元
(2)乙商店,见解析
【分析】本题考查列代数式解决实际问题.根据题意正确的列出代数式是解题的关键.
(1)根据题意,列出代数式即可;
(2)将时代入两个代数式进行求值,再将时代入两个代数式进行求值,通过比较数值的大小即可得解.
【详解】(1)解:甲商店的付款费用为:(元)
乙商店的付款费用为:(元)
(2)解:当时:
去甲商店的付款费用为:元;
去乙商店的付款费用为:元;
∵,
∴去甲商店购买;
当时:
去甲商店的付款费用为:元;
去乙商店的付款费用为:元;
∵,
∴去乙商店购买;
∴购买15盒乒乓球时,到甲商店购买更便宜;购买25盒乒乓球时,到乙商店购买更便宜.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
