鲁教版七年级上册期末综合测试卷(含答案)
文档属性
| 名称 | 鲁教版七年级上册期末综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 12.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 14:41:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末综合测试卷
时间: 90分钟 满分: 120分
一、选择题(每题4分,共48分)
1.下列各数中,为有理数的是 ( )
A. B.3.232 232 223… C.
2.已知一个三角形两边长分别为2,6,则第三边长可以为 ( )
A. 3 B. 4 C. 7 D. 9
3.下面四种化学仪器的示意图是轴对称图形的是 ( )
4.下列一次函数中,y随x 的增大而减小的函数是 ( )
5.△ABC的三条边长分别为a,b,c,对应的三个内角分别为∠A,∠B,∠C,则满足下列条件的△ABC是直角三角形的是 ( )
6.已知点与点 关于 x轴对称,那么a,b的值为 ( )
7.如图,在△ABC 和△DEF 中, AC = DF,添加下列哪一个条件无法证明△ABC≌△DEF ( )
8.如图,在△ABC中,∠A=90°,BC的垂直平分线 DE 交 BC 于点E,交 AB 于点 D,若 BC=15,AC=9,则△ACD的周长为 ( )
A. 16 B. 21 C. 24 D. 26
第8题图 第9题图
9.如图,在 Rt△ABC中,∠ACB=90°,若AB=15,则正方形 ADEC和正方形 BCFG的面积之和为( )
A. 225 B. 200 C. 150 D.无法计算
10.估算 的值在 ( )
A.1到2 之间 B.2到3之间 C.3到4之间 D.4到5之间
11.利用计算器求 的值,正确的按键顺序为 ( )
12.已知点 点 点C 是关于x的一次函数图象上的三点,的大小关系为 ( )
二、填空题(每题4分,共20分)
13.将一次函数y=x-1的图象沿 y轴向上平移3个单位长度,所得直线对应的函数表达式为_________.
的平方根是____________.
15.如图,直线 与相交于点,则关于x 的方程 的解是_____________.
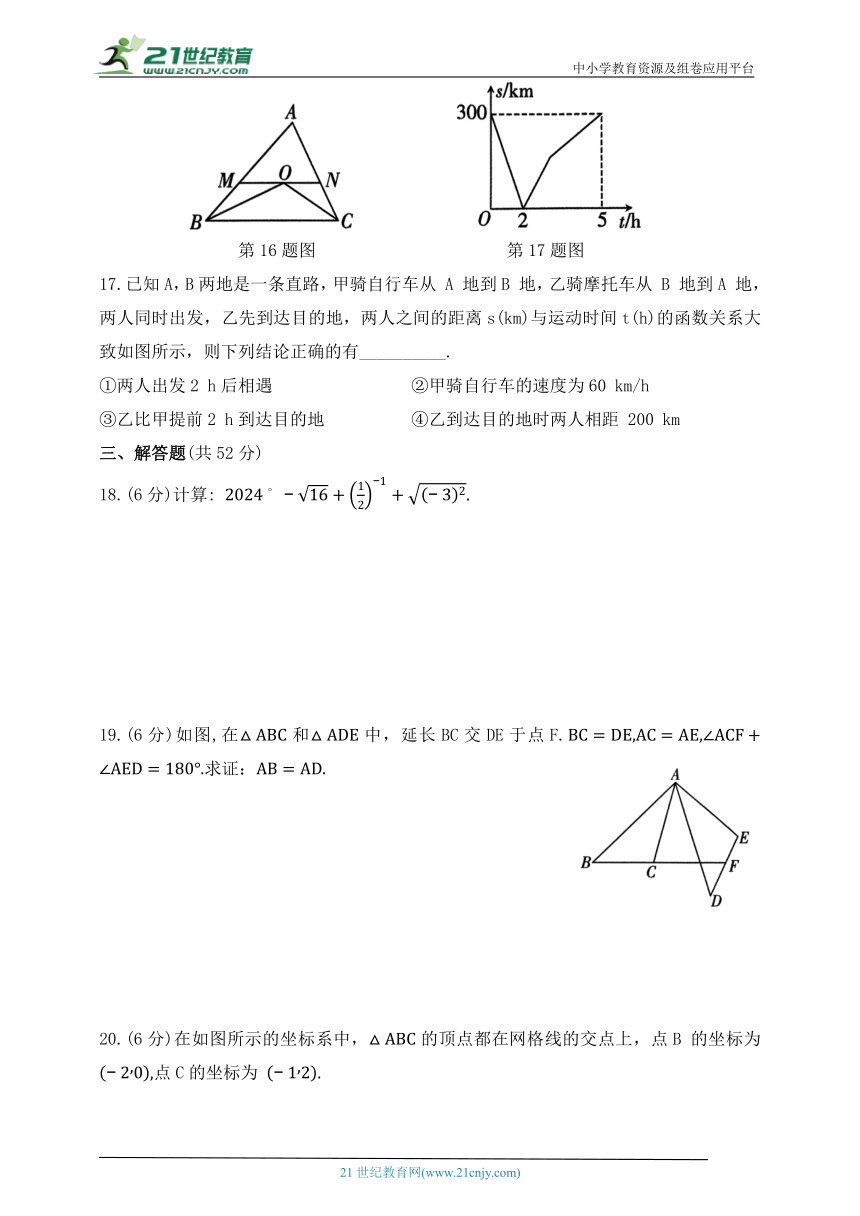
16.如图,在 中,的角平分线交于点 O,MN过点 O,且 ∥分别交 AB,AC于点 M,N.若 则
第16题图 第17题图
17.已知A,B两地是一条直路,甲骑自行车从 A 地到B 地,乙骑摩托车从 B 地到A 地,两人同时出发,乙先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,则下列结论正确的有__________.
①两人出发2 h后相遇 ②甲骑自行车的速度为60 km/h
③乙比甲提前2 h到达目的地 ④乙到达目的地时两人相距 200 km
三、解答题(共52分)
18.(6分)计算:
19.(6分)如图,在和中,延长BC交DE于点F.求证:
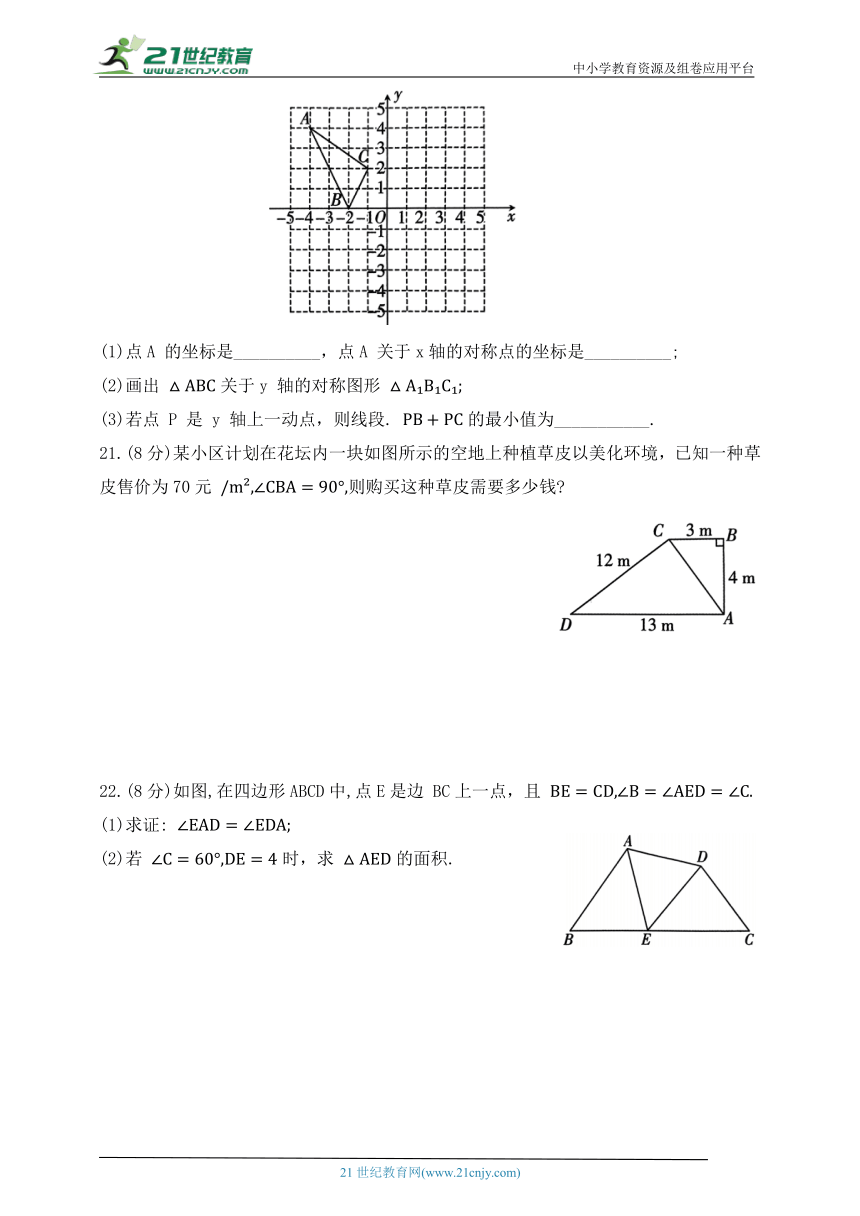
20.(6分)在如图所示的坐标系中,的顶点都在网格线的交点上,点B 的坐标为点C的坐标为
(1)点A 的坐标是__________,点A 关于x轴的对称点的坐标是__________;
(2)画出 关于y 轴的对称图形
(3)若点 P 是 y 轴上一动点,则线段. 的最小值为___________.
21.(8分)某小区计划在花坛内一块如图所示的空地上种植草皮以美化环境,已知一种草皮售价为70元 则购买这种草皮需要多少钱
22.(8分)如图,在四边形ABCD中,点E是边 BC上一点,且
(1)求证:
(2)若 时,求 的面积.
23.(8分)如图所示,过点 A(2,0)的两条直线 分别交 y轴于点B,C,其中点 B 在原点上方,点C 在原点下方,已知
(1)求点 B 的坐标;
(2)若 的面积为4,求 的表达式.
24.(10分)甲、乙两个工程组同时挖掘沈白高铁某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务,甲、乙两组挖掘的长度之和y(m)与甲组挖掘时间x(天)之间的关系如图所示.
(1)甲组比乙组多挖掘了_________天;
(2)求乙组停工后y关于x的函数表达式,并写出自变量x的取值范围;
(3)当甲组挖掘的总长度与乙组挖掘的总长度相等时,直接写出乙组已停工的天数.
参考答案
1. A 2. C 3. C 4. D 5. C 6. B 7. A 8. B 9. A 10. B
11. D 12. A
15. 16.5
17.①②④ 解析:因为横轴表示运动时间,纵轴表示两人之间的距离,所以图上的第一个点(0,300),表示甲、乙两人还未出发时,相距300 km,也就是A,B 两地相距300 km,第二个点(2,0),表示甲、乙两人出发2小时时,两人相距0米,即相遇,故①正确;最后一个点(5,300)表示行驶得慢的甲5 小时行驶完300千米,也到了自己的目的地,此时两人相距300千米,所以甲骑自行车的速度为300÷5=60(km/h),故②正确;因为甲、乙两小时相遇,共走完300 km,所以甲、乙的速度和=300÷2=150(km/h),所以乙的速度=150-60=90(km/h).所以乙走完全程的时间 所以乙比甲提前到达的时间为 故③不正确;乙到达目的地A时,走了 此时甲离开A地的路程为 此时两人相距200(km),故④正确.
18.解:
19.证明:因为∠ACB+∠ACF = ∠ACF+∠AED=180°,所以∠ACB=∠AED,
在△ABC和△ADE中, 所以△ABC≌△ADE(SAS),所以AB=AD.
20.解:(1)由坐标系得点A 的坐标为(-4,4),点 A 关于x轴对称点的坐标为(-4,-4).
故答案为:(-4,4),(-4,-4);
(2)△ABC关于y轴的对称图形 如图所示;
(3)如图,连接交y轴于点 P,连接 CP,此时 最小, 故答案为:
21.解:因为 由勾股定理,得
所以
因为 所以
所以 是直角三角形,且 为直角.
所以
购买这种草皮需要的钱为36×70=2520(元).
答:购买这种草坪需要2 520元.
22.解:(1)证明:因为∠B =∠AED=∠C, ∠AEC=180°-∠AEB = 180°-(180°-∠B-∠BAE)=∠B+∠BAE=∠AED+∠CED,所以∠BAE=∠CED,
在△ABE和△ECD中, 所以△ABE≌△ECD(AAS),所以AE=ED,
所以∠EAD=∠EDA;
(2)因为∠AED=∠C=60°,AE=ED,所以△AED为等边三角形,所以AE=AD=ED=4,
过A点作AF⊥ED于点 F,所以
由勾股定理得 即 所以
所以 (或
23.解:(1)在 Rt△AOB中, 所以 所以OB=3,所以点 B 的坐标是(0,3);
(2)因为 所以 ·2=4,解得 BC=4.所以C(0,-1).
设 把A(2,0)代入,得2k-1=0,解得 所以l 的表达式为
24.解:(1)由图象可知,甲、乙合作共挖掘了30天,甲单独挖掘了60-30=30天,即甲组比乙组多挖掘了30天.故答案为:30;
(2)设乙组停工后 y关于x的函数表达式为y= kx+b,点(30,210)(60,300)在图象上,
则 30k+b=210,60k+b=300,解得 k=3,b=120.
所以函数表达式为 y=3x+120(30≤x≤60);
(3)由(2)表达式可知,甲单独干了30天,挖掘的长度是300-210=90(m),甲的工作效率是3m/天.
前30天是甲、乙合作共挖掘了210m,则乙单独挖掘的长度是210-90=120(m).
当甲挖掘的长度是 120 m 时,工作天数是120÷3=40(天),
乙组已停工的天数是40-30=10(天).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末综合测试卷
时间: 90分钟 满分: 120分
一、选择题(每题4分,共48分)
1.下列各数中,为有理数的是 ( )
A. B.3.232 232 223… C.
2.已知一个三角形两边长分别为2,6,则第三边长可以为 ( )
A. 3 B. 4 C. 7 D. 9
3.下面四种化学仪器的示意图是轴对称图形的是 ( )
4.下列一次函数中,y随x 的增大而减小的函数是 ( )
5.△ABC的三条边长分别为a,b,c,对应的三个内角分别为∠A,∠B,∠C,则满足下列条件的△ABC是直角三角形的是 ( )
6.已知点与点 关于 x轴对称,那么a,b的值为 ( )
7.如图,在△ABC 和△DEF 中, AC = DF,添加下列哪一个条件无法证明△ABC≌△DEF ( )
8.如图,在△ABC中,∠A=90°,BC的垂直平分线 DE 交 BC 于点E,交 AB 于点 D,若 BC=15,AC=9,则△ACD的周长为 ( )
A. 16 B. 21 C. 24 D. 26
第8题图 第9题图
9.如图,在 Rt△ABC中,∠ACB=90°,若AB=15,则正方形 ADEC和正方形 BCFG的面积之和为( )
A. 225 B. 200 C. 150 D.无法计算
10.估算 的值在 ( )
A.1到2 之间 B.2到3之间 C.3到4之间 D.4到5之间
11.利用计算器求 的值,正确的按键顺序为 ( )
12.已知点 点 点C 是关于x的一次函数图象上的三点,的大小关系为 ( )
二、填空题(每题4分,共20分)
13.将一次函数y=x-1的图象沿 y轴向上平移3个单位长度,所得直线对应的函数表达式为_________.
的平方根是____________.
15.如图,直线 与相交于点,则关于x 的方程 的解是_____________.
16.如图,在 中,的角平分线交于点 O,MN过点 O,且 ∥分别交 AB,AC于点 M,N.若 则
第16题图 第17题图
17.已知A,B两地是一条直路,甲骑自行车从 A 地到B 地,乙骑摩托车从 B 地到A 地,两人同时出发,乙先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,则下列结论正确的有__________.
①两人出发2 h后相遇 ②甲骑自行车的速度为60 km/h
③乙比甲提前2 h到达目的地 ④乙到达目的地时两人相距 200 km
三、解答题(共52分)
18.(6分)计算:
19.(6分)如图,在和中,延长BC交DE于点F.求证:
20.(6分)在如图所示的坐标系中,的顶点都在网格线的交点上,点B 的坐标为点C的坐标为
(1)点A 的坐标是__________,点A 关于x轴的对称点的坐标是__________;
(2)画出 关于y 轴的对称图形
(3)若点 P 是 y 轴上一动点,则线段. 的最小值为___________.
21.(8分)某小区计划在花坛内一块如图所示的空地上种植草皮以美化环境,已知一种草皮售价为70元 则购买这种草皮需要多少钱
22.(8分)如图,在四边形ABCD中,点E是边 BC上一点,且
(1)求证:
(2)若 时,求 的面积.
23.(8分)如图所示,过点 A(2,0)的两条直线 分别交 y轴于点B,C,其中点 B 在原点上方,点C 在原点下方,已知
(1)求点 B 的坐标;
(2)若 的面积为4,求 的表达式.
24.(10分)甲、乙两个工程组同时挖掘沈白高铁某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务,甲、乙两组挖掘的长度之和y(m)与甲组挖掘时间x(天)之间的关系如图所示.
(1)甲组比乙组多挖掘了_________天;
(2)求乙组停工后y关于x的函数表达式,并写出自变量x的取值范围;
(3)当甲组挖掘的总长度与乙组挖掘的总长度相等时,直接写出乙组已停工的天数.
参考答案
1. A 2. C 3. C 4. D 5. C 6. B 7. A 8. B 9. A 10. B
11. D 12. A
15. 16.5
17.①②④ 解析:因为横轴表示运动时间,纵轴表示两人之间的距离,所以图上的第一个点(0,300),表示甲、乙两人还未出发时,相距300 km,也就是A,B 两地相距300 km,第二个点(2,0),表示甲、乙两人出发2小时时,两人相距0米,即相遇,故①正确;最后一个点(5,300)表示行驶得慢的甲5 小时行驶完300千米,也到了自己的目的地,此时两人相距300千米,所以甲骑自行车的速度为300÷5=60(km/h),故②正确;因为甲、乙两小时相遇,共走完300 km,所以甲、乙的速度和=300÷2=150(km/h),所以乙的速度=150-60=90(km/h).所以乙走完全程的时间 所以乙比甲提前到达的时间为 故③不正确;乙到达目的地A时,走了 此时甲离开A地的路程为 此时两人相距200(km),故④正确.
18.解:
19.证明:因为∠ACB+∠ACF = ∠ACF+∠AED=180°,所以∠ACB=∠AED,
在△ABC和△ADE中, 所以△ABC≌△ADE(SAS),所以AB=AD.
20.解:(1)由坐标系得点A 的坐标为(-4,4),点 A 关于x轴对称点的坐标为(-4,-4).
故答案为:(-4,4),(-4,-4);
(2)△ABC关于y轴的对称图形 如图所示;
(3)如图,连接交y轴于点 P,连接 CP,此时 最小, 故答案为:
21.解:因为 由勾股定理,得
所以
因为 所以
所以 是直角三角形,且 为直角.
所以
购买这种草皮需要的钱为36×70=2520(元).
答:购买这种草坪需要2 520元.
22.解:(1)证明:因为∠B =∠AED=∠C, ∠AEC=180°-∠AEB = 180°-(180°-∠B-∠BAE)=∠B+∠BAE=∠AED+∠CED,所以∠BAE=∠CED,
在△ABE和△ECD中, 所以△ABE≌△ECD(AAS),所以AE=ED,
所以∠EAD=∠EDA;
(2)因为∠AED=∠C=60°,AE=ED,所以△AED为等边三角形,所以AE=AD=ED=4,
过A点作AF⊥ED于点 F,所以
由勾股定理得 即 所以
所以 (或
23.解:(1)在 Rt△AOB中, 所以 所以OB=3,所以点 B 的坐标是(0,3);
(2)因为 所以 ·2=4,解得 BC=4.所以C(0,-1).
设 把A(2,0)代入,得2k-1=0,解得 所以l 的表达式为
24.解:(1)由图象可知,甲、乙合作共挖掘了30天,甲单独挖掘了60-30=30天,即甲组比乙组多挖掘了30天.故答案为:30;
(2)设乙组停工后 y关于x的函数表达式为y= kx+b,点(30,210)(60,300)在图象上,
则 30k+b=210,60k+b=300,解得 k=3,b=120.
所以函数表达式为 y=3x+120(30≤x≤60);
(3)由(2)表达式可知,甲单独干了30天,挖掘的长度是300-210=90(m),甲的工作效率是3m/天.
前30天是甲、乙合作共挖掘了210m,则乙单独挖掘的长度是210-90=120(m).
当甲挖掘的长度是 120 m 时,工作天数是120÷3=40(天),
乙组已停工的天数是40-30=10(天).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
