第六章 一次函数 3 一次函数的图象 第2课时 一次函数的图象及性质 同步练习(含答案)
文档属性
| 名称 | 第六章 一次函数 3 一次函数的图象 第2课时 一次函数的图象及性质 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
3 一次函数的图象
第2课时 一次函数的图象及性质
1.一次函数 的图象不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.对于某个一次函数 根据两位同学的对话得出的结论,错误的是( )
3.若一次函数的图象如图所示,则下列说法正确的是 ( )
A. k>0 B. b=2 C. y 随x的增大而增大 D. x=3时,y=0
4.在一次函数 中,y的值随x值的增大而增大,且,则点 在 ( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
5.在平面直角坐标系中,将直线 沿 y轴向下平移6个单位长度后,得到一条新的直线,该直线与x轴的交点坐标是 ( )
A.(0,3) B.(-2,0) C.(4,0) D.(6,0)
6.直线 与直线 平行,且与y轴交点的纵坐标是3,那么 ( )
7.在同一平面直角坐标系中,函数和(a为常数,的图象可能是( )
8.在直角坐标系中,已知点 A点 是直线上的两点,则m,n的大小关系是 ( )
9.如图,已知直线 与坐标轴分别交于 A,B两点,那么过原点O且将 △AOB 的面积平分的直线 的表达式为 ( )
10.函数的图象经过点(2,5),则___________.
11.若直线 向上平移3个单位长度后经过点(2,m),则m的值为__________.
12.在一次函数 中,y随x的增大而增大,则k的值可以是_________(任写一个符合条件的数即可).
13.一次函数 的图象经过(a,b)(c,d),则
14.甲、乙两位同学各给出某函数的一个特征,甲:“函数值y随自变量x增大而减小”;乙:“函数图象经过点(0,2)”,请你写出一个同时满足这两个特征的函数,其表达式是______________.
15.如图,与图中直线 关于x 轴对称的直线的函数表达式是____________.
16.函数 的图象与x轴,y轴分别交于A,B两点,点 C在x轴上,若 为等腰三角形,则满足条件的点 C共有_________个.
17.已知一次函数
(1)求出图象与x轴,y轴的交点A,B 的坐标,并画出函数的图象;
(2)求A,B两点之间的距离;
(3)求出 的面积.
18.直线的表达式为 分别交x 轴,y轴于点 A,B.
(1)写出A,B两点的坐标,并画出直线的图象;
(2)将直线向上平移4 个单位长度得到交x轴于点C.作出 的图象,并求 的表达式.
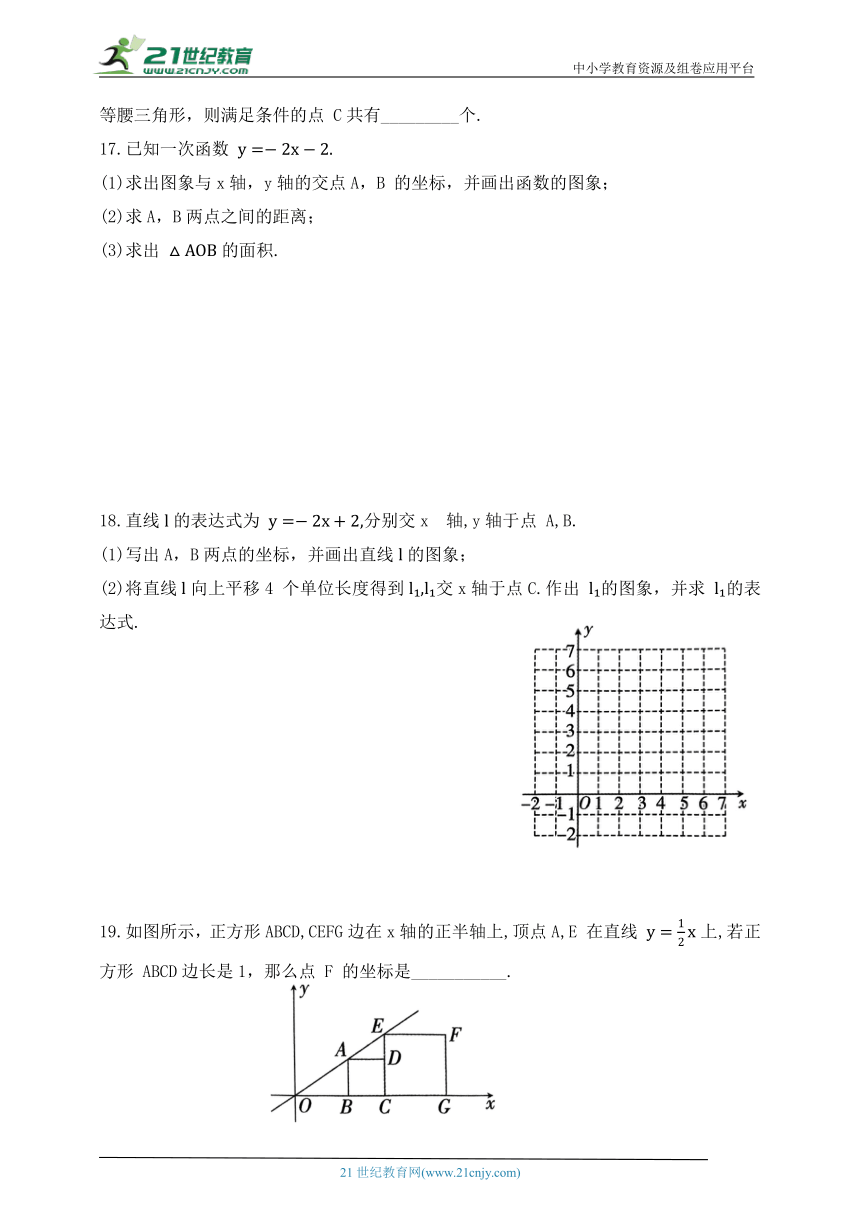
19.如图所示,正方形ABCD,CEFG边在x轴的正半轴上,顶点A,E 在直线 上,若正方形 ABCD边长是1,那么点 F 的坐标是___________.
20.平面直角坐标系中,点在直线 上,点在 x 轴上, ,是等腰直角三角形如果点 那么 的纵坐标是____________.
参考答案
1. D 2. C 3. B 4. B 5. B 6. A 7. D 8. A 9. D
10. 1 11. 5 12. 3(答案不唯一)
13.25 解析:将 P(a,b),Q(c,d)分别代入表达式y=x+5得a+5=b,c+5=d,
整理得a-b=-5,c-d=-5,所以a(c-d)-b(c-d)=-5a+5b=5(b-a)=5×5=25.
14.(示例)y=-2x+2 15. y=x-1 16. 4
17.解:(1)当y=0时,-2x-2=0,解得x=-1,所以点 A 的坐标是(-1,0).
当x=0时,y=-2,所以点 B 的坐标是(0,-2).
画函数图象,如图所示;
(2)因为点 A 的坐标为( 点 B 的坐标为 所以
由勾股定理,得
所以A,B两点之间的距离为
所以 的面积为1.
18.解:(1)当. 时,解得. 即点A(1,0),
当 时, 即点 B(0,2).直线如图所示;
(2)直线 的表达式为 直线 如图所示.
解析: 因 为 正 方 形 ABCD,CEFG边在x轴的正半轴上,
所以 EF=GF,AB,CD,CE, 轴,
因为顶点A,E在直线
令 则 所以点A(2,1),所以点 E 的横坐标为3,
将x=3代入直线 得 所以点 E,F的纵坐标是 即
所以点 F 的横坐标为 即点
解析:如图,过点 作 轴于过点 作 轴于 过点 作轴于
设
因为点 所以
因为 为等腰直角三角形,且所以
同理可得 2m,
所以
所以点 A 的坐标为( 点 的坐标为
因为点 A (1,1)在直线 上,所以 解得
所以该直线的表达式为
因为点 在直线 上,所以 解得
因为点 在直线 上,
所以 整理得4n=6+2m,
将 代入 得 所以点. 的纵坐标为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 一次函数
3 一次函数的图象
第2课时 一次函数的图象及性质
1.一次函数 的图象不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.对于某个一次函数 根据两位同学的对话得出的结论,错误的是( )
3.若一次函数的图象如图所示,则下列说法正确的是 ( )
A. k>0 B. b=2 C. y 随x的增大而增大 D. x=3时,y=0
4.在一次函数 中,y的值随x值的增大而增大,且,则点 在 ( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
5.在平面直角坐标系中,将直线 沿 y轴向下平移6个单位长度后,得到一条新的直线,该直线与x轴的交点坐标是 ( )
A.(0,3) B.(-2,0) C.(4,0) D.(6,0)
6.直线 与直线 平行,且与y轴交点的纵坐标是3,那么 ( )
7.在同一平面直角坐标系中,函数和(a为常数,的图象可能是( )
8.在直角坐标系中,已知点 A点 是直线上的两点,则m,n的大小关系是 ( )
9.如图,已知直线 与坐标轴分别交于 A,B两点,那么过原点O且将 △AOB 的面积平分的直线 的表达式为 ( )
10.函数的图象经过点(2,5),则___________.
11.若直线 向上平移3个单位长度后经过点(2,m),则m的值为__________.
12.在一次函数 中,y随x的增大而增大,则k的值可以是_________(任写一个符合条件的数即可).
13.一次函数 的图象经过(a,b)(c,d),则
14.甲、乙两位同学各给出某函数的一个特征,甲:“函数值y随自变量x增大而减小”;乙:“函数图象经过点(0,2)”,请你写出一个同时满足这两个特征的函数,其表达式是______________.
15.如图,与图中直线 关于x 轴对称的直线的函数表达式是____________.
16.函数 的图象与x轴,y轴分别交于A,B两点,点 C在x轴上,若 为等腰三角形,则满足条件的点 C共有_________个.
17.已知一次函数
(1)求出图象与x轴,y轴的交点A,B 的坐标,并画出函数的图象;
(2)求A,B两点之间的距离;
(3)求出 的面积.
18.直线的表达式为 分别交x 轴,y轴于点 A,B.
(1)写出A,B两点的坐标,并画出直线的图象;
(2)将直线向上平移4 个单位长度得到交x轴于点C.作出 的图象,并求 的表达式.
19.如图所示,正方形ABCD,CEFG边在x轴的正半轴上,顶点A,E 在直线 上,若正方形 ABCD边长是1,那么点 F 的坐标是___________.
20.平面直角坐标系中,点在直线 上,点在 x 轴上, ,是等腰直角三角形如果点 那么 的纵坐标是____________.
参考答案
1. D 2. C 3. B 4. B 5. B 6. A 7. D 8. A 9. D
10. 1 11. 5 12. 3(答案不唯一)
13.25 解析:将 P(a,b),Q(c,d)分别代入表达式y=x+5得a+5=b,c+5=d,
整理得a-b=-5,c-d=-5,所以a(c-d)-b(c-d)=-5a+5b=5(b-a)=5×5=25.
14.(示例)y=-2x+2 15. y=x-1 16. 4
17.解:(1)当y=0时,-2x-2=0,解得x=-1,所以点 A 的坐标是(-1,0).
当x=0时,y=-2,所以点 B 的坐标是(0,-2).
画函数图象,如图所示;
(2)因为点 A 的坐标为( 点 B 的坐标为 所以
由勾股定理,得
所以A,B两点之间的距离为
所以 的面积为1.
18.解:(1)当. 时,解得. 即点A(1,0),
当 时, 即点 B(0,2).直线如图所示;
(2)直线 的表达式为 直线 如图所示.
解析: 因 为 正 方 形 ABCD,CEFG边在x轴的正半轴上,
所以 EF=GF,AB,CD,CE, 轴,
因为顶点A,E在直线
令 则 所以点A(2,1),所以点 E 的横坐标为3,
将x=3代入直线 得 所以点 E,F的纵坐标是 即
所以点 F 的横坐标为 即点
解析:如图,过点 作 轴于过点 作 轴于 过点 作轴于
设
因为点 所以
因为 为等腰直角三角形,且所以
同理可得 2m,
所以
所以点 A 的坐标为( 点 的坐标为
因为点 A (1,1)在直线 上,所以 解得
所以该直线的表达式为
因为点 在直线 上,所以 解得
因为点 在直线 上,
所以 整理得4n=6+2m,
将 代入 得 所以点. 的纵坐标为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
