第六章 一次函数 5 一次函数的应用 第1课时 一次函数的简单应用 同步练习(含答案)
文档属性
| 名称 | 第六章 一次函数 5 一次函数的应用 第1课时 一次函数的简单应用 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 14:38:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
5 一次函数的应用
第1课时 一次函数的简单应用
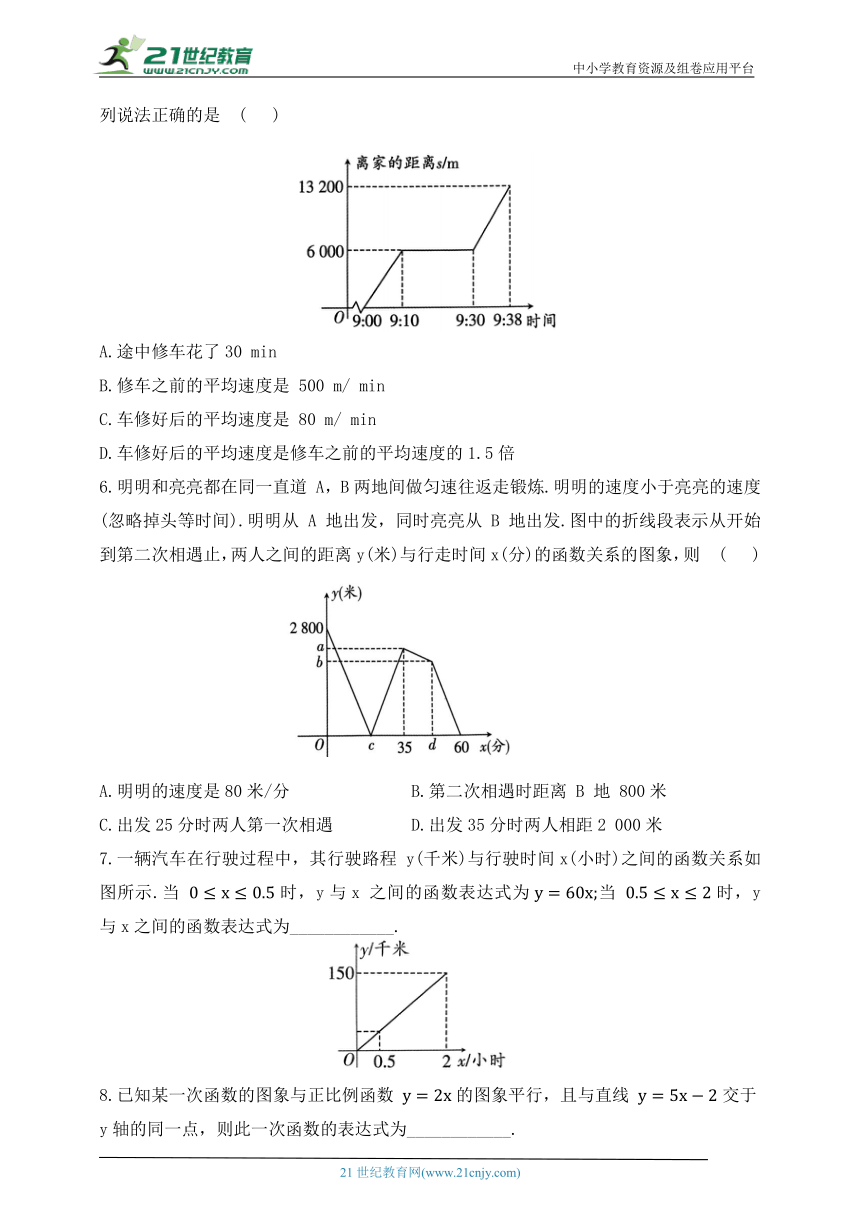
1.如图,直线 过点A(6,0)和点 则方程 的解是 ( )
第1题图 第2题图
2.小明从家出发到商场购物后返回,如图表示的是小明离家的路程s(m)与时间t(min)之间的函数关系,已知小明购物用时30 min,返回速度是去商场的速度的1.2倍,则 a的值为 ( )
A. 46 B. 48 C. 50 D. 52
3.已知方程 kx+b=0的解是x=3,则函数的图象可能是 ( )
4.有一个装有水的容器,如图所示,注水之前容器内有少量水,现向容器内注水,并同时开始计时,在注水过程中,水面高度匀速增加,则容器注满水之前,将容器内的水面高度 y(cm)与时间x(秒)记录于如表,则★的值是 ( )
x/秒 5 10 25 30
y/cm 11 12 15 ★
A. 16 B. 17 C. 18 D. 19
5.第11 届中国(湖南)矿物宝石国际博览会在郴州市举行,小方一家上午9:00开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.以下是他们家出发后离家的距离s与时间的函数图象.分析图中信息,下列说法正确的是 ( )
A.途中修车花了30 min
B.修车之前的平均速度是 500 m/ min
C.车修好后的平均速度是 80 m/ min
D.车修好后的平均速度是修车之前的平均速度的1.5倍
6.明明和亮亮都在同一直道 A,B两地间做匀速往返走锻炼.明明的速度小于亮亮的速度(忽略掉头等时间).明明从 A 地出发,同时亮亮从 B 地出发.图中的折线段表示从开始到第二次相遇止,两人之间的距离y(米)与行走时间x(分)的函数关系的图象,则 ( )
A.明明的速度是80米/分 B.第二次相遇时距离 B 地 800米
C.出发25分时两人第一次相遇 D.出发35分时两人相距2 000米
7.一辆汽车在行驶过程中,其行驶路程 y(千米)与行驶时间x(小时)之间的函数关系如图所示.当 时,y与x 之间的函数表达式为当 时,y与x之间的函数表达式为____________.
8.已知某一次函数的图象与正比例函数 的图象平行,且与直线 交于y轴的同一点,则此一次函数的表达式为____________.
9.一次函数 为常数,且的图象如图所示,根据图象信息可求得关于x的方程的解为____________.
第9题图 第10题图
10.某摩托车的油箱最多可存油5 升,行驶时油箱内的余油量y(L)与行驶路程s(km)成一次函数关系,其图象如图所示,摩托车加满油后最多能行驶__________ km.
11.某次气象探测活动中,在一广场上同时释放两个探测气球,1号探测气球从距离地面5米处出发,以1米/分的速度上升,2号探测气球距离地面的高度 y(单位:米)与上升时间x(单位:分)满足一次函数关系,其图象如图所示.
(1)求y关于x的函数表达式;
(2)探测气球上升多长时间时,两个气球位于同一高度 此时它们距离地面多少米
12.已知:一次函数 ,x与y的对应值如表所示,根据表中数据分析,下列结论正确的是 ( )
x … -1 0 1 2 3 …
y … 5 3 1 -1 -3 …
A. y随x的增大而增大
B.一次函数 的图象经过一、二、三象限
C.关于x的方程 kx+b=0的解是.
D.一次函数. 与x轴的交点坐标是(1.5,0)
13.某农科所对当地小麦从抽穗期到灌浆期连续51 天的累计需水量进行研究,得到当地每公顷小麦在这51天内累计需水量 与天数x之间的关系如图所示,其中,线段OA,AC 分别表示抽穗期、灌浆期的 y与x 之间的函数关系.
(1)求这51天内,y与x之间的函数关系式;
(2)求当地每公顷小麦在整个灌浆期的需水量.
参考答案
1. B 2. D 3. C 4. A 5. D
6. B 解析:因为第一次相遇两人共走了2800米,第二次相遇两人共走了3×2800米,且二者速度不变,所以60÷3=20,
所以出发20分时两人第一次相遇,C选项错误;
亮亮的速度为2 800÷35=80(米/分),两人的速度和为2 800÷20=140(米/分),
明明的速度为140-80=60(米/分),A 选项错误;
第二次相遇时距离 B地距离为60×60-2800=800(米),B选项正确;
出发35 分钟时两人间的距离为60×35=2100(米),D选项错误.
10.165
11.解:(1)由题意,可设y关于x的函数表达式为y= kx+b(k≠0),
由题意,得b=15,30k+b=30,所以
所以y关于x的函数表达式为
(2)由题意,可知1号气球上升x分时高度为(x+5)米,由题意,
得 解得x=20,
当x=20时,
所以上升20分钟时,两个气球位于同一高度,此时它们距离地面25米.
12. D
13.解:(1)由题意,当0≤x≤20时,设y= kx,
所以20k=960,所以k=48,所以y=48x.
当20由题意,得20m+n=960,40m+n=1660,解得m=35,n=260.所以y=35x+260.
综上所述, 所求函数关系式为
(2)由题意,令x=51,所以y=35×51+260=2045.
又当x=20时,y=960,所以每公顷小麦在整个灌浆期的需水量=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 一次函数
5 一次函数的应用
第1课时 一次函数的简单应用
1.如图,直线 过点A(6,0)和点 则方程 的解是 ( )
第1题图 第2题图
2.小明从家出发到商场购物后返回,如图表示的是小明离家的路程s(m)与时间t(min)之间的函数关系,已知小明购物用时30 min,返回速度是去商场的速度的1.2倍,则 a的值为 ( )
A. 46 B. 48 C. 50 D. 52
3.已知方程 kx+b=0的解是x=3,则函数的图象可能是 ( )
4.有一个装有水的容器,如图所示,注水之前容器内有少量水,现向容器内注水,并同时开始计时,在注水过程中,水面高度匀速增加,则容器注满水之前,将容器内的水面高度 y(cm)与时间x(秒)记录于如表,则★的值是 ( )
x/秒 5 10 25 30
y/cm 11 12 15 ★
A. 16 B. 17 C. 18 D. 19
5.第11 届中国(湖南)矿物宝石国际博览会在郴州市举行,小方一家上午9:00开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.以下是他们家出发后离家的距离s与时间的函数图象.分析图中信息,下列说法正确的是 ( )
A.途中修车花了30 min
B.修车之前的平均速度是 500 m/ min
C.车修好后的平均速度是 80 m/ min
D.车修好后的平均速度是修车之前的平均速度的1.5倍
6.明明和亮亮都在同一直道 A,B两地间做匀速往返走锻炼.明明的速度小于亮亮的速度(忽略掉头等时间).明明从 A 地出发,同时亮亮从 B 地出发.图中的折线段表示从开始到第二次相遇止,两人之间的距离y(米)与行走时间x(分)的函数关系的图象,则 ( )
A.明明的速度是80米/分 B.第二次相遇时距离 B 地 800米
C.出发25分时两人第一次相遇 D.出发35分时两人相距2 000米
7.一辆汽车在行驶过程中,其行驶路程 y(千米)与行驶时间x(小时)之间的函数关系如图所示.当 时,y与x 之间的函数表达式为当 时,y与x之间的函数表达式为____________.
8.已知某一次函数的图象与正比例函数 的图象平行,且与直线 交于y轴的同一点,则此一次函数的表达式为____________.
9.一次函数 为常数,且的图象如图所示,根据图象信息可求得关于x的方程的解为____________.
第9题图 第10题图
10.某摩托车的油箱最多可存油5 升,行驶时油箱内的余油量y(L)与行驶路程s(km)成一次函数关系,其图象如图所示,摩托车加满油后最多能行驶__________ km.
11.某次气象探测活动中,在一广场上同时释放两个探测气球,1号探测气球从距离地面5米处出发,以1米/分的速度上升,2号探测气球距离地面的高度 y(单位:米)与上升时间x(单位:分)满足一次函数关系,其图象如图所示.
(1)求y关于x的函数表达式;
(2)探测气球上升多长时间时,两个气球位于同一高度 此时它们距离地面多少米
12.已知:一次函数 ,x与y的对应值如表所示,根据表中数据分析,下列结论正确的是 ( )
x … -1 0 1 2 3 …
y … 5 3 1 -1 -3 …
A. y随x的增大而增大
B.一次函数 的图象经过一、二、三象限
C.关于x的方程 kx+b=0的解是.
D.一次函数. 与x轴的交点坐标是(1.5,0)
13.某农科所对当地小麦从抽穗期到灌浆期连续51 天的累计需水量进行研究,得到当地每公顷小麦在这51天内累计需水量 与天数x之间的关系如图所示,其中,线段OA,AC 分别表示抽穗期、灌浆期的 y与x 之间的函数关系.
(1)求这51天内,y与x之间的函数关系式;
(2)求当地每公顷小麦在整个灌浆期的需水量.
参考答案
1. B 2. D 3. C 4. A 5. D
6. B 解析:因为第一次相遇两人共走了2800米,第二次相遇两人共走了3×2800米,且二者速度不变,所以60÷3=20,
所以出发20分时两人第一次相遇,C选项错误;
亮亮的速度为2 800÷35=80(米/分),两人的速度和为2 800÷20=140(米/分),
明明的速度为140-80=60(米/分),A 选项错误;
第二次相遇时距离 B地距离为60×60-2800=800(米),B选项正确;
出发35 分钟时两人间的距离为60×35=2100(米),D选项错误.
10.165
11.解:(1)由题意,可设y关于x的函数表达式为y= kx+b(k≠0),
由题意,得b=15,30k+b=30,所以
所以y关于x的函数表达式为
(2)由题意,可知1号气球上升x分时高度为(x+5)米,由题意,
得 解得x=20,
当x=20时,
所以上升20分钟时,两个气球位于同一高度,此时它们距离地面25米.
12. D
13.解:(1)由题意,当0≤x≤20时,设y= kx,
所以20k=960,所以k=48,所以y=48x.
当20
综上所述, 所求函数关系式为
(2)由题意,令x=51,所以y=35×51+260=2045.
又当x=20时,y=960,所以每公顷小麦在整个灌浆期的需水量=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
