第六章 一次函数 5 一次函数的应用 第2课时 两个一次函数的综合应用 同步练习(含答案)
文档属性
| 名称 | 第六章 一次函数 5 一次函数的应用 第2课时 两个一次函数的综合应用 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 14:44:18 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
5 一次函数的应用
第2课时 两个一次函数的综合应用
1.A,B 两地相距20千米,甲、乙两人都从 A 地去B 地,图中 和 分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法错误的是 ( )
A.乙晚出发1小时 B.乙出发3小时后追上甲
C.甲的速度是4千米/时 D.乙先到达B地
第1题图 第2题图
2.如图所示, 分别是甲、乙两弹簧的长y(cm)与所挂物体质量x(kg)之间函数关系的图象,设甲弹簧每挂1 kg物体伸长的长度为k 甲 cm,乙弹簧每挂 1 kg 物体伸长的长度为 则 k甲与 的关系是 ( )
D.不能确定
3.数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点 P,根据图象可知,方程的解是 ( )
第3题图 第4题图
4.如图,一次函数的图象相交于点 P,则关于x 的方程 的解是 ( )
5.甲、乙两车沿同一路线从 A城出发前往 B 城,在整个行程中,汽车离开A 城的距离y 与时刻t 的对应关系如图所示,关于下列结论:①A,B两城相距300 km ②甲车的平均速度是60km/h,乙车的平均速度是 100 km/h ③乙车先出发,先到达B 城 ④甲车在9:30追上乙车.正确的有 ( )
A.①② B.①③ C.②④ D.①④
第5题图 第6题图
6.我国古代数学经典著作《九章算术》记载:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之.问几何步及之 ”如图是善行者与不善行者行走路程s(单位:步)关于善行者的行走时间 t的函数图象,则两图象交点 P 的纵坐标是___________.
7.学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,两人各自从家同时同向出发,沿同一条路匀速前进,如图所示, 和 分别表示两人到小亮家的距离s(km)和时间t(h)的关系,则出发________h后两人相遇.
第7题图 第8题图
8.如图,记录了某公司产品的一天的销售收入与销售量的关系用 表示,销售成本与销售量的关系用 表示.求:
(1)l 的函数表达式:______________;
(2)l 的函数表达式:______________;
(3)当销售量等于__________台时,销售收入等于销售成本.
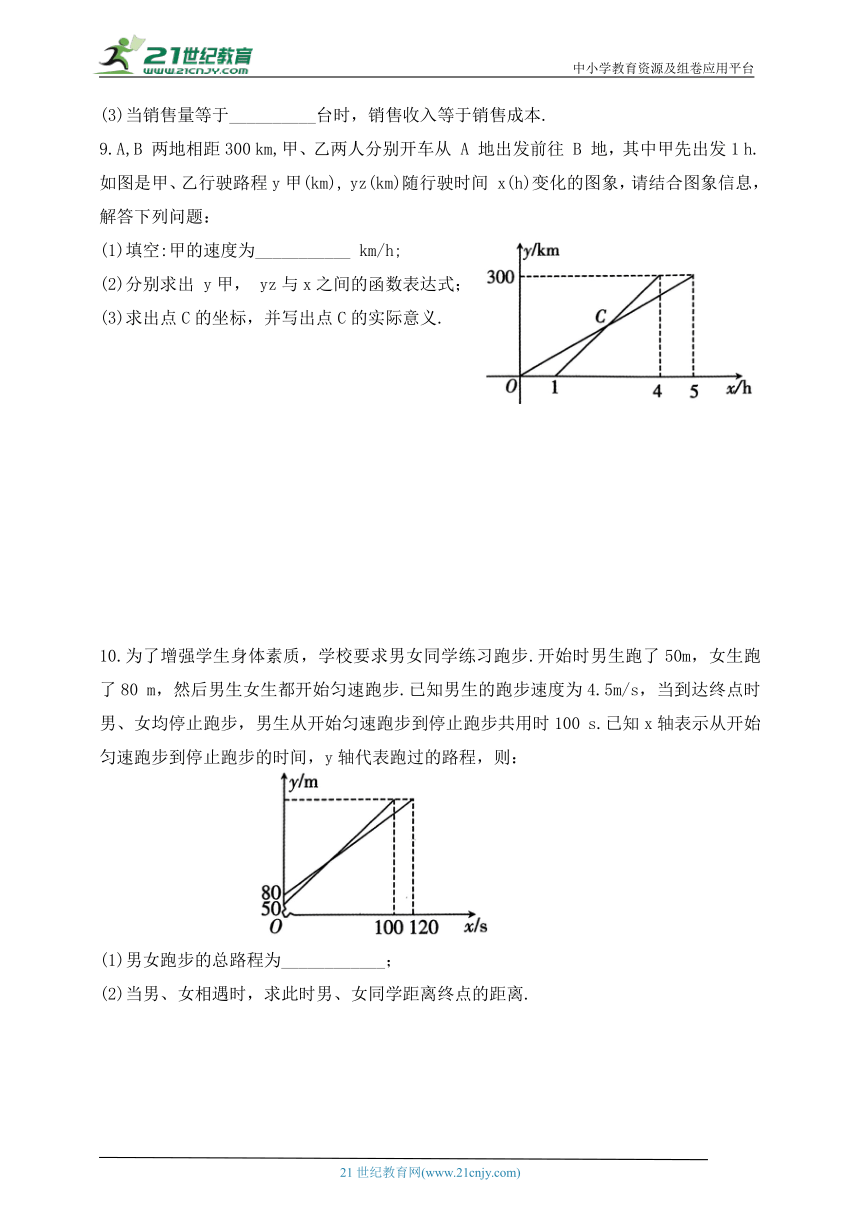
9.A,B 两地相距300 km,甲、乙两人分别开车从 A 地出发前往 B 地,其中甲先出发1 h. 如图是甲、乙行驶路程y甲(km), yz(km)随行驶时间 x(h)变化的图象,请结合图象信息,解答下列问题:
(1)填空:甲的速度为___________ km/h;
(2)分别求出 y甲, yz与x之间的函数表达式;
(3)求出点C的坐标,并写出点C的实际意义.
10.为了增强学生身体素质,学校要求男女同学练习跑步.开始时男生跑了50m,女生跑了80 m,然后男生女生都开始匀速跑步.已知男生的跑步速度为4.5m/s,当到达终点时男、女均停止跑步,男生从开始匀速跑步到停止跑步共用时100 s.已知x轴表示从开始匀速跑步到停止跑步的时间,y轴代表跑过的路程,则:
(1)男女跑步的总路程为____________;
(2)当男、女相遇时,求此时男、女同学距离终点的距离.
11.一条笔直的路上依次有 M,P,N三地,其中 M,N 两地相距 1 000 米.甲、乙两机器人分别从 M,N两地同时出发,去目的地 N,M,匀速而行.图中 OA,BC分别表示甲、乙机器人离 M 地的距离y(米)与行走时间x(分钟)的函数关系图象.
(1)求OA 所在直线的表达式;
(2)出发后甲机器人行走多少时间,与乙机器人相遇
(3)甲机器人到 P 地后,再经过1分钟乙机器人也到 P 地,求P,M两地间的距离.
12.1 号探测气球从海拔 10 m处出发,以 的速度竖直上升.与此同时,2号探测气球从海拔 2 0 m 处出发,以a m/ min的速度竖直上升.两个气球都上升了 1 h.1号、2号气球所在位置的海拔 (单位:m)与上升时间x(单位: min)的函数关系如图所示.请根据图象回答下列问题:
(2)请分别求出 y ,y 与x的函数关系式;
(3)当上升多长时间时,两个气球的海拔竖直高度差为5m
参考答案
1. B 2. A 3. A 4. D 5. D 6. 250 7. 0.35
8.解:(1)设 的函数表达式为
根据题意,得 所以
所以 的函数表达式是 故答案为:
(2)设 的函数表达式为
因为直线过(0,100),(2, 200)两点,所以 解得 k=50,
所以 的函数表达式是 y=50x+100,故答案为:y=50x+100;
(3)从图象上看,当销售量等于2台时,销售收入等于销售成本,故答案为:2.
9.解:(1)甲的速度为300÷5=60(km/h),故答案为:60;
(2)由(1)可知,y甲与x之间的函数表达式为
设 yz与x之间的函数表达式为
根据题意,得k+b=0,4k+b=300,解得 k=100,b=-100.所以 yz=100x-100(1≤x≤4);
(3)根据题意,得60x=100x-100,解得x=2.5,60×2.5=150(km),
所以点C的坐标为(2.5,150),
故点 C的实际意义是甲车出发 2.5h 后被乙车追上,此时两车行驶了 150 km.
10.(1)解:因为开始时男生跑了50m,男生的跑步速度为4.5m/s,从开始匀速跑步到停止跑步共用时100s.
所以男生跑步的路程为50+4.5×100=500 m,所以男女跑步的总路程为500×2=1000 m,
故答案为:1 000 m;
(2)男生从开始匀速跑步到停止跑步的直线表达式为y=50+4.5x,
设女生从开始匀速跑步到停止跑步的直线表达式为y= kx+80,
依题意,女生匀速跑了500-80=420 m,用了120 s,则速度为420÷120=3.5(m/s),
所以y=3.5x+80,
由50+4.5x=3.5x+80,解得x=30,将x=30代入y=50+4.5x,解得y=185,
所以此时男、女同学距离终点的距离为500-185=315 m.
11.解:(1)由图象可知,OA 所在直线为正比例函数,所以设
因为A(5,1 000),所以OA 所在直线的表达式为
(2)由图可知甲机器人速度为 200(米/分钟),
乙机器人速度为: (米/分钟),
两人相遇时: (分钟),
答:出发后甲机器人行走 分钟,与乙机器人相遇;
(3)设甲机器人行走 t分钟时到 P 地,P地与M 地距离为 200t,
则乙机器人( 分钟后到 P 地,P 地与 M地距离
由 解得 所以
答:P,M 两地间的距离为 600米.
12.解:(1)因为1号探测气球从海拔10 m处出发,以1m / min的速度竖直上升.与此同时,2号探测气球从海拔20 m处出发,以 的速度竖直上升.
当 时,两球相遇, 所以
设2号探测气球表达式为
因为 过(20,30),所以 解得 所以
故答案为:0.5,30;
(2)根据题意,得1号探测气球所在位置的海拔:
2号探测气球所在位置的海拔: 0.5x;
(3)分两种情况:
①2号探测气球比1号探测气球海拔高5米,
根据题意,得解得
②1号探测气球比2号探测气球海拔高5米,
根据题意,得解得
综上所述,上升了10 或30 min后这两个气球的海拔竖直高度差为5 m .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 一次函数
5 一次函数的应用
第2课时 两个一次函数的综合应用
1.A,B 两地相距20千米,甲、乙两人都从 A 地去B 地,图中 和 分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法错误的是 ( )
A.乙晚出发1小时 B.乙出发3小时后追上甲
C.甲的速度是4千米/时 D.乙先到达B地
第1题图 第2题图
2.如图所示, 分别是甲、乙两弹簧的长y(cm)与所挂物体质量x(kg)之间函数关系的图象,设甲弹簧每挂1 kg物体伸长的长度为k 甲 cm,乙弹簧每挂 1 kg 物体伸长的长度为 则 k甲与 的关系是 ( )
D.不能确定
3.数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点 P,根据图象可知,方程的解是 ( )
第3题图 第4题图
4.如图,一次函数的图象相交于点 P,则关于x 的方程 的解是 ( )
5.甲、乙两车沿同一路线从 A城出发前往 B 城,在整个行程中,汽车离开A 城的距离y 与时刻t 的对应关系如图所示,关于下列结论:①A,B两城相距300 km ②甲车的平均速度是60km/h,乙车的平均速度是 100 km/h ③乙车先出发,先到达B 城 ④甲车在9:30追上乙车.正确的有 ( )
A.①② B.①③ C.②④ D.①④
第5题图 第6题图
6.我国古代数学经典著作《九章算术》记载:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之.问几何步及之 ”如图是善行者与不善行者行走路程s(单位:步)关于善行者的行走时间 t的函数图象,则两图象交点 P 的纵坐标是___________.
7.学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,两人各自从家同时同向出发,沿同一条路匀速前进,如图所示, 和 分别表示两人到小亮家的距离s(km)和时间t(h)的关系,则出发________h后两人相遇.
第7题图 第8题图
8.如图,记录了某公司产品的一天的销售收入与销售量的关系用 表示,销售成本与销售量的关系用 表示.求:
(1)l 的函数表达式:______________;
(2)l 的函数表达式:______________;
(3)当销售量等于__________台时,销售收入等于销售成本.
9.A,B 两地相距300 km,甲、乙两人分别开车从 A 地出发前往 B 地,其中甲先出发1 h. 如图是甲、乙行驶路程y甲(km), yz(km)随行驶时间 x(h)变化的图象,请结合图象信息,解答下列问题:
(1)填空:甲的速度为___________ km/h;
(2)分别求出 y甲, yz与x之间的函数表达式;
(3)求出点C的坐标,并写出点C的实际意义.
10.为了增强学生身体素质,学校要求男女同学练习跑步.开始时男生跑了50m,女生跑了80 m,然后男生女生都开始匀速跑步.已知男生的跑步速度为4.5m/s,当到达终点时男、女均停止跑步,男生从开始匀速跑步到停止跑步共用时100 s.已知x轴表示从开始匀速跑步到停止跑步的时间,y轴代表跑过的路程,则:
(1)男女跑步的总路程为____________;
(2)当男、女相遇时,求此时男、女同学距离终点的距离.
11.一条笔直的路上依次有 M,P,N三地,其中 M,N 两地相距 1 000 米.甲、乙两机器人分别从 M,N两地同时出发,去目的地 N,M,匀速而行.图中 OA,BC分别表示甲、乙机器人离 M 地的距离y(米)与行走时间x(分钟)的函数关系图象.
(1)求OA 所在直线的表达式;
(2)出发后甲机器人行走多少时间,与乙机器人相遇
(3)甲机器人到 P 地后,再经过1分钟乙机器人也到 P 地,求P,M两地间的距离.
12.1 号探测气球从海拔 10 m处出发,以 的速度竖直上升.与此同时,2号探测气球从海拔 2 0 m 处出发,以a m/ min的速度竖直上升.两个气球都上升了 1 h.1号、2号气球所在位置的海拔 (单位:m)与上升时间x(单位: min)的函数关系如图所示.请根据图象回答下列问题:
(2)请分别求出 y ,y 与x的函数关系式;
(3)当上升多长时间时,两个气球的海拔竖直高度差为5m
参考答案
1. B 2. A 3. A 4. D 5. D 6. 250 7. 0.35
8.解:(1)设 的函数表达式为
根据题意,得 所以
所以 的函数表达式是 故答案为:
(2)设 的函数表达式为
因为直线过(0,100),(2, 200)两点,所以 解得 k=50,
所以 的函数表达式是 y=50x+100,故答案为:y=50x+100;
(3)从图象上看,当销售量等于2台时,销售收入等于销售成本,故答案为:2.
9.解:(1)甲的速度为300÷5=60(km/h),故答案为:60;
(2)由(1)可知,y甲与x之间的函数表达式为
设 yz与x之间的函数表达式为
根据题意,得k+b=0,4k+b=300,解得 k=100,b=-100.所以 yz=100x-100(1≤x≤4);
(3)根据题意,得60x=100x-100,解得x=2.5,60×2.5=150(km),
所以点C的坐标为(2.5,150),
故点 C的实际意义是甲车出发 2.5h 后被乙车追上,此时两车行驶了 150 km.
10.(1)解:因为开始时男生跑了50m,男生的跑步速度为4.5m/s,从开始匀速跑步到停止跑步共用时100s.
所以男生跑步的路程为50+4.5×100=500 m,所以男女跑步的总路程为500×2=1000 m,
故答案为:1 000 m;
(2)男生从开始匀速跑步到停止跑步的直线表达式为y=50+4.5x,
设女生从开始匀速跑步到停止跑步的直线表达式为y= kx+80,
依题意,女生匀速跑了500-80=420 m,用了120 s,则速度为420÷120=3.5(m/s),
所以y=3.5x+80,
由50+4.5x=3.5x+80,解得x=30,将x=30代入y=50+4.5x,解得y=185,
所以此时男、女同学距离终点的距离为500-185=315 m.
11.解:(1)由图象可知,OA 所在直线为正比例函数,所以设
因为A(5,1 000),所以OA 所在直线的表达式为
(2)由图可知甲机器人速度为 200(米/分钟),
乙机器人速度为: (米/分钟),
两人相遇时: (分钟),
答:出发后甲机器人行走 分钟,与乙机器人相遇;
(3)设甲机器人行走 t分钟时到 P 地,P地与M 地距离为 200t,
则乙机器人( 分钟后到 P 地,P 地与 M地距离
由 解得 所以
答:P,M 两地间的距离为 600米.
12.解:(1)因为1号探测气球从海拔10 m处出发,以1m / min的速度竖直上升.与此同时,2号探测气球从海拔20 m处出发,以 的速度竖直上升.
当 时,两球相遇, 所以
设2号探测气球表达式为
因为 过(20,30),所以 解得 所以
故答案为:0.5,30;
(2)根据题意,得1号探测气球所在位置的海拔:
2号探测气球所在位置的海拔: 0.5x;
(3)分两种情况:
①2号探测气球比1号探测气球海拔高5米,
根据题意,得解得
②1号探测气球比2号探测气球海拔高5米,
根据题意,得解得
综上所述,上升了10 或30 min后这两个气球的海拔竖直高度差为5 m .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
