第六章 一次函数 章末复习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
章末复习
类型一 函数的定义
1.如表所示为一个图案中红色和白色瓷砖数量的关系.设r和ω分别为红色和白色瓷砖的数量,下列函数表达式可以表示 w与r之间的关系的是 ( )
红色瓷砖数量(r) 3 4 5 6 7
白色瓷砖数量(w) 6 8 10 12 14
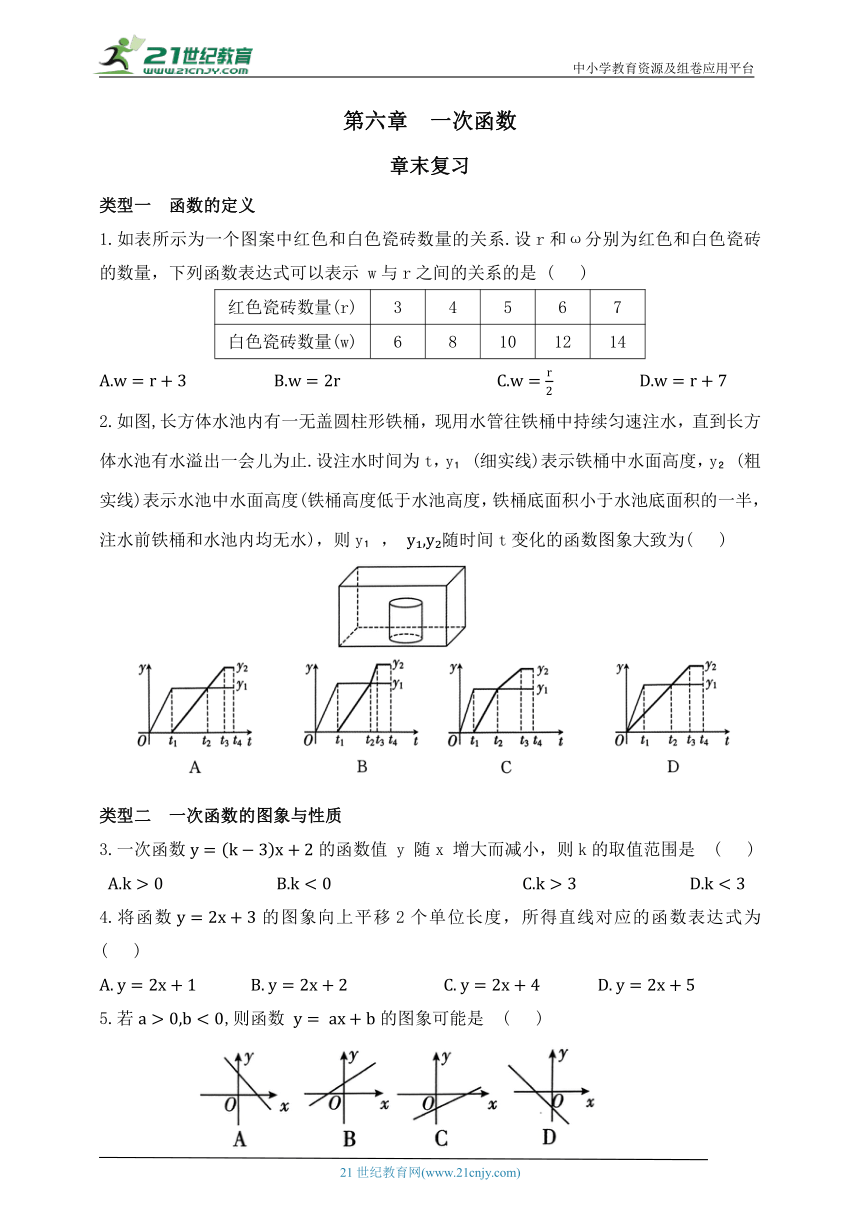
2.如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为t,y (细实线)表示铁桶中水面高度,y (粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则y , 随时间t变化的函数图象大致为( )
类型二 一次函数的图象与性质
3.一次函数的函数值 y 随x 增大而减小,则k的取值范围是 ( )
4.将函数的图象向上平移2个单位长度,所得直线对应的函数表达式为 ( )
5.若,则函数 的图象可能是 ( )
6.一次函数的图象经过点 P,且y的值随x 值的增大而增大,则点 P 的坐标可以为 ( )
A.(-5,3) B.(1,-3) C.(2,2) D.(5,-1)
7.已知一次函数.求:
(1)m,n是什么数时,y随x的增大而增大;
(2)m,n是什么数时,函数图象与 y轴的交点在x轴下方;
(3)m,n是什么数时,函数图象经过原点;
(4)若m=-1,n=2,求此函数图象与两坐标轴的交点坐标.
类型三 次函数与方程
8.如图,已知一次函数 的图象与x轴,y轴分别交于点(2,0),点(0,3),关于x的方程 的解是 ( )
C. x=0 D.不能确定
9.若关于x的方程的解为则直线与x轴的交点坐标为________.
10.如图,直线 与相交于点 P(1,2),则关于x的方程的解是___________.
类型四 确定一次函数的关系式
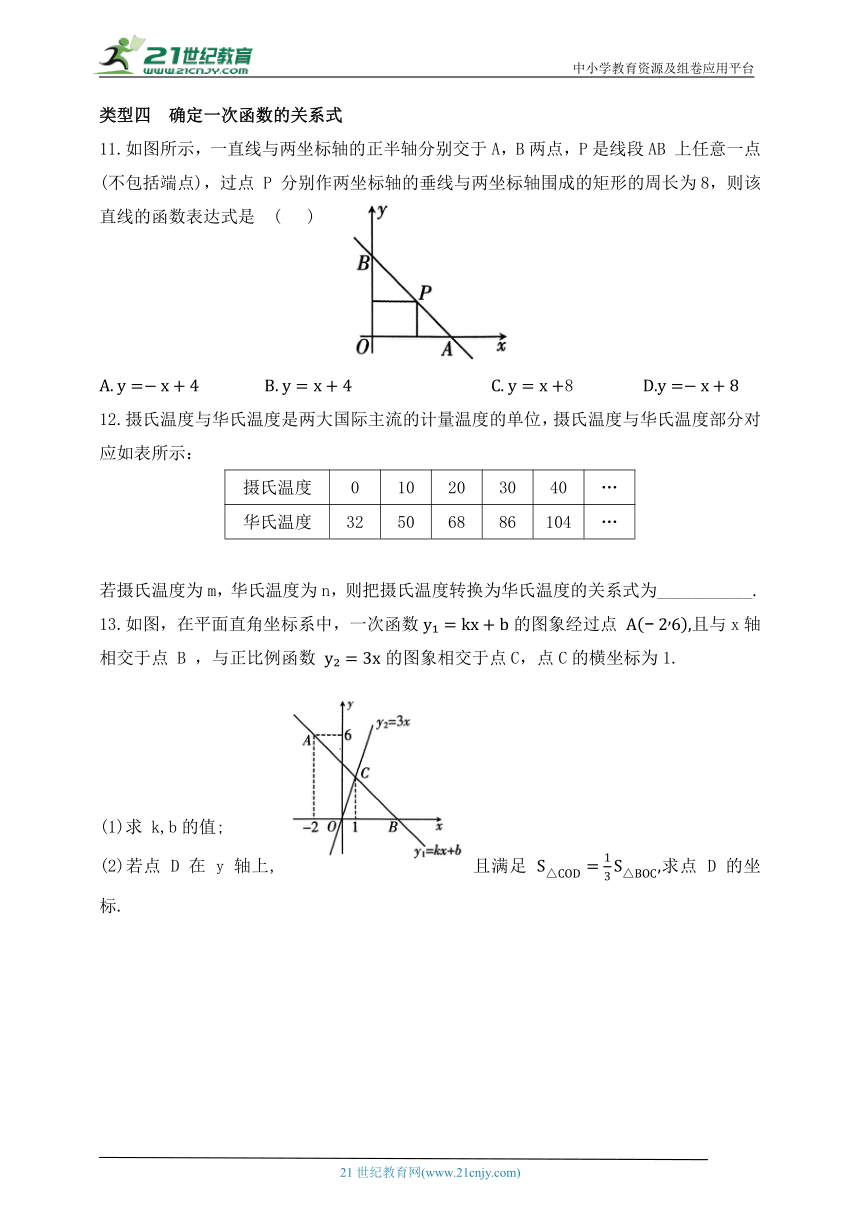
11.如图所示,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB 上任意一点(不包括端点),过点 P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是 ( )
8
12.摄氏温度与华氏温度是两大国际主流的计量温度的单位,摄氏温度与华氏温度部分对应如表所示:
摄氏温度 0 10 20 30 40 …
华氏温度 32 50 68 86 104 …
若摄氏温度为m,华氏温度为n,则把摄氏温度转换为华氏温度的关系式为___________.
13.如图,在平面直角坐标系中,一次函数的图象经过点 且与x轴相交于点 B ,与正比例函数 的图象相交于点C,点C的横坐标为1.
(1)求 k,b的值;
(2)若点 D 在 y 轴上,且满足 求点 D 的坐标.
类型五 一次函数的应用
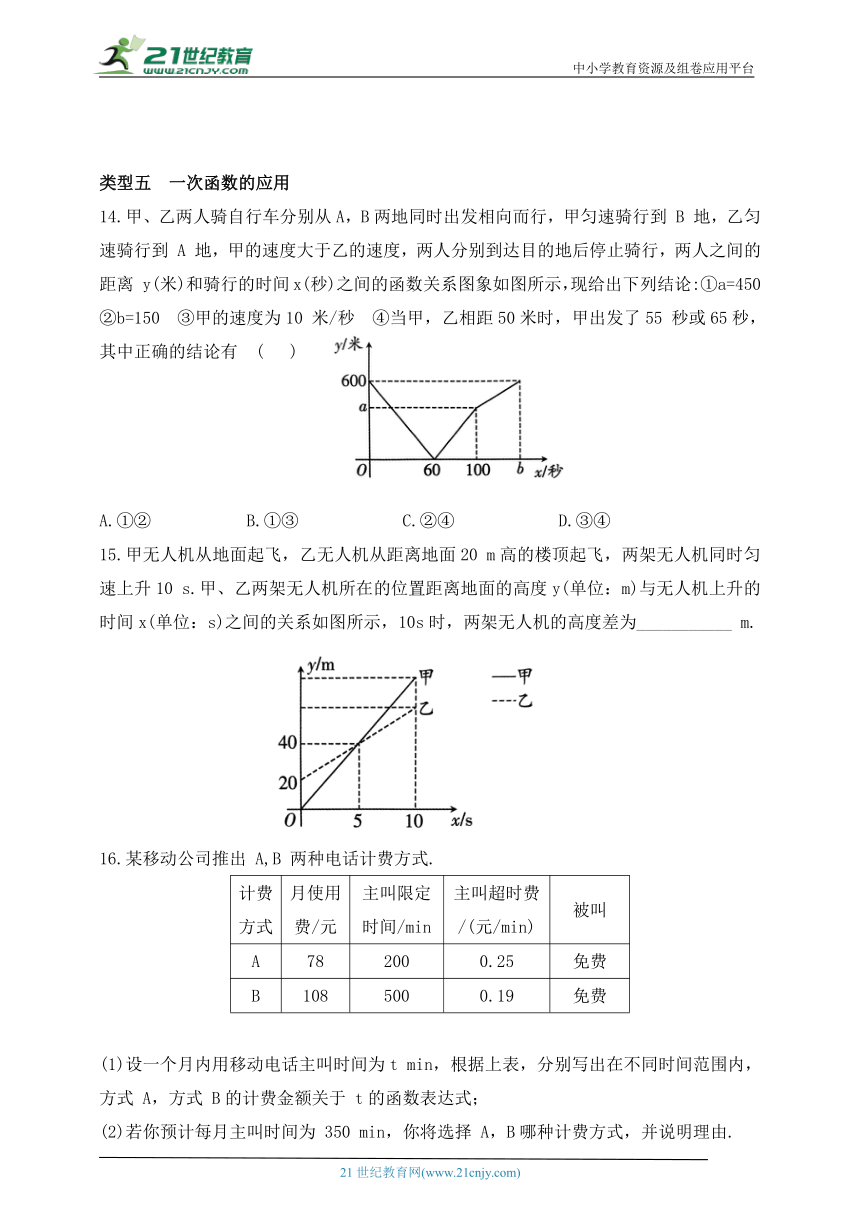
14.甲、乙两人骑自行车分别从A,B两地同时出发相向而行,甲匀速骑行到 B 地,乙匀速骑行到 A 地,甲的速度大于乙的速度,两人分别到达目的地后停止骑行,两人之间的距离 y(米)和骑行的时间x(秒)之间的函数关系图象如图所示,现给出下列结论:①a=450 ②b=150 ③甲的速度为10 米/秒 ④当甲,乙相距50米时,甲出发了55 秒或65秒,其中正确的结论有 ( )
A.①② B.①③ C.②④ D.③④
15.甲无人机从地面起飞,乙无人机从距离地面20 m高的楼顶起飞,两架无人机同时匀速上升10 s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示,10s时,两架无人机的高度差为___________ m.
16.某移动公司推出 A,B 两种电话计费方式.
计费方式 月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
A 78 200 0.25 免费
B 108 500 0.19 免费
(1)设一个月内用移动电话主叫时间为t min,根据上表,分别写出在不同时间范围内,方式 A,方式 B的计费金额关于 t的函数表达式;
(2)若你预计每月主叫时间为 350 min,你将选择 A,B哪种计费方式,并说明理由.
17.甲、乙两人相约登山,他们同时从入口处出发,甲步行登山到山顶,乙先步行15分钟到缆车站,再乘坐缆车直达山顶.甲、乙距山脚的垂直高度 y(米)与甲登山的时间x(分钟)之间的函数图象如图所示:
(1)当15≤x≤40时,求乙距山脚的垂直高度 y与x之间的函数关系式;
(2)求乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度.
参考答案
1. B 2. C 3. D 4. D 5. C 6. C
7.解:(1)由题意得 y随x的增大而增大,则 解得m>-2.
则当 且n为任意实数时,y随x的增大而增大;
(2)由题意得 所以m≠-2,且n>3;
(3)由题意得 所以m≠-2,且n=3;
(4)当m=-1,n=2时,一次函数为
令 即与y轴交于(0,1),
令 即与x轴交于
8. A 9. (2,0) 10. x=1 11. A 12.
13.解:(1)当x=1时, 所以点C的坐标为(1,3).
将A(-2,6),C(1,3)代入. 得6=-2k+b,3=k+b,
所以b=6+2k,b=3-k,所以6+2k=3-k,解得 k=-1,b=4;
(2)当 时,有-x+4=0,解得x=4,所以点 B的坐标为(4,0).
设点 D的坐标为(0,m),
因为 即 解得m=-4或m=4,
所以点 D 的坐标为(0,4)或(
14. C 解析:由图可得,甲的速度为 (米/秒),故③错误,不符合题意;
乙的速度为 (米/秒),,故①错误,不符合题意;
,故②正确,符合题意;
设当甲、乙相距50米时,甲出发了m秒,两人相遇前:解得
两人相遇后:( 解得 ;故④正确,符合题意.
15.20 解析:设甲无人机所在的位置距离地面的高度 y甲与无人机上升的时间x之间的函数关系为
因为当x=5时, 所以 解得 所以
设乙无人机所在的位置距离地面的高度 yz与无人机上升的时间x之间的函数关系为
因为当. 时, 当 时, 40,
所以 解得 所以
当 时,
所以10s时,两架无人机的高度差为20m.
16.解:(1)设方式 A的计费金额. (元),方式B 的计费金额y (元),
根据表格数据可知,当0≤t≤200时, 78;当t>200时,
0.25t+28;
当0≤t≤500时, 当t>500时, 108+0.19(t-500)=0.19t+13;
综上所述,
(2)选择方式 B计费,理由:
当每月主叫时间为 350 min时,
因为115.5>108,所以选择方式B计费.
17.解:(1)设乙距山脚的垂直高度 y与x之间的函数关系式为y= kx+b,
因为直线过(15,0)和(40,300),所以15k+b=0,40k+b=300,解得k=12,b=-180,
所以乙距山脚的垂直高度 y与x之间的函数关系式为y=12x-180;
(2)当 25≤x≤60时,设甲的函数表达式为y= mx+n,
将(25,160)和(60,300)代入,得160=25m+n,300=60m+n,解得m=4,n=60,所以y=4x+60;
因为乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度相等,所以12x-180=4x+60,解得. 所以
所以乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度为180 米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 一次函数
章末复习
类型一 函数的定义
1.如表所示为一个图案中红色和白色瓷砖数量的关系.设r和ω分别为红色和白色瓷砖的数量,下列函数表达式可以表示 w与r之间的关系的是 ( )
红色瓷砖数量(r) 3 4 5 6 7
白色瓷砖数量(w) 6 8 10 12 14
2.如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为t,y (细实线)表示铁桶中水面高度,y (粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则y , 随时间t变化的函数图象大致为( )
类型二 一次函数的图象与性质
3.一次函数的函数值 y 随x 增大而减小,则k的取值范围是 ( )
4.将函数的图象向上平移2个单位长度,所得直线对应的函数表达式为 ( )
5.若,则函数 的图象可能是 ( )
6.一次函数的图象经过点 P,且y的值随x 值的增大而增大,则点 P 的坐标可以为 ( )
A.(-5,3) B.(1,-3) C.(2,2) D.(5,-1)
7.已知一次函数.求:
(1)m,n是什么数时,y随x的增大而增大;
(2)m,n是什么数时,函数图象与 y轴的交点在x轴下方;
(3)m,n是什么数时,函数图象经过原点;
(4)若m=-1,n=2,求此函数图象与两坐标轴的交点坐标.
类型三 次函数与方程
8.如图,已知一次函数 的图象与x轴,y轴分别交于点(2,0),点(0,3),关于x的方程 的解是 ( )
C. x=0 D.不能确定
9.若关于x的方程的解为则直线与x轴的交点坐标为________.
10.如图,直线 与相交于点 P(1,2),则关于x的方程的解是___________.
类型四 确定一次函数的关系式
11.如图所示,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB 上任意一点(不包括端点),过点 P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是 ( )
8
12.摄氏温度与华氏温度是两大国际主流的计量温度的单位,摄氏温度与华氏温度部分对应如表所示:
摄氏温度 0 10 20 30 40 …
华氏温度 32 50 68 86 104 …
若摄氏温度为m,华氏温度为n,则把摄氏温度转换为华氏温度的关系式为___________.
13.如图,在平面直角坐标系中,一次函数的图象经过点 且与x轴相交于点 B ,与正比例函数 的图象相交于点C,点C的横坐标为1.
(1)求 k,b的值;
(2)若点 D 在 y 轴上,且满足 求点 D 的坐标.
类型五 一次函数的应用
14.甲、乙两人骑自行车分别从A,B两地同时出发相向而行,甲匀速骑行到 B 地,乙匀速骑行到 A 地,甲的速度大于乙的速度,两人分别到达目的地后停止骑行,两人之间的距离 y(米)和骑行的时间x(秒)之间的函数关系图象如图所示,现给出下列结论:①a=450 ②b=150 ③甲的速度为10 米/秒 ④当甲,乙相距50米时,甲出发了55 秒或65秒,其中正确的结论有 ( )
A.①② B.①③ C.②④ D.③④
15.甲无人机从地面起飞,乙无人机从距离地面20 m高的楼顶起飞,两架无人机同时匀速上升10 s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示,10s时,两架无人机的高度差为___________ m.
16.某移动公司推出 A,B 两种电话计费方式.
计费方式 月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
A 78 200 0.25 免费
B 108 500 0.19 免费
(1)设一个月内用移动电话主叫时间为t min,根据上表,分别写出在不同时间范围内,方式 A,方式 B的计费金额关于 t的函数表达式;
(2)若你预计每月主叫时间为 350 min,你将选择 A,B哪种计费方式,并说明理由.
17.甲、乙两人相约登山,他们同时从入口处出发,甲步行登山到山顶,乙先步行15分钟到缆车站,再乘坐缆车直达山顶.甲、乙距山脚的垂直高度 y(米)与甲登山的时间x(分钟)之间的函数图象如图所示:
(1)当15≤x≤40时,求乙距山脚的垂直高度 y与x之间的函数关系式;
(2)求乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度.
参考答案
1. B 2. C 3. D 4. D 5. C 6. C
7.解:(1)由题意得 y随x的增大而增大,则 解得m>-2.
则当 且n为任意实数时,y随x的增大而增大;
(2)由题意得 所以m≠-2,且n>3;
(3)由题意得 所以m≠-2,且n=3;
(4)当m=-1,n=2时,一次函数为
令 即与y轴交于(0,1),
令 即与x轴交于
8. A 9. (2,0) 10. x=1 11. A 12.
13.解:(1)当x=1时, 所以点C的坐标为(1,3).
将A(-2,6),C(1,3)代入. 得6=-2k+b,3=k+b,
所以b=6+2k,b=3-k,所以6+2k=3-k,解得 k=-1,b=4;
(2)当 时,有-x+4=0,解得x=4,所以点 B的坐标为(4,0).
设点 D的坐标为(0,m),
因为 即 解得m=-4或m=4,
所以点 D 的坐标为(0,4)或(
14. C 解析:由图可得,甲的速度为 (米/秒),故③错误,不符合题意;
乙的速度为 (米/秒),,故①错误,不符合题意;
,故②正确,符合题意;
设当甲、乙相距50米时,甲出发了m秒,两人相遇前:解得
两人相遇后:( 解得 ;故④正确,符合题意.
15.20 解析:设甲无人机所在的位置距离地面的高度 y甲与无人机上升的时间x之间的函数关系为
因为当x=5时, 所以 解得 所以
设乙无人机所在的位置距离地面的高度 yz与无人机上升的时间x之间的函数关系为
因为当. 时, 当 时, 40,
所以 解得 所以
当 时,
所以10s时,两架无人机的高度差为20m.
16.解:(1)设方式 A的计费金额. (元),方式B 的计费金额y (元),
根据表格数据可知,当0≤t≤200时, 78;当t>200时,
0.25t+28;
当0≤t≤500时, 当t>500时, 108+0.19(t-500)=0.19t+13;
综上所述,
(2)选择方式 B计费,理由:
当每月主叫时间为 350 min时,
因为115.5>108,所以选择方式B计费.
17.解:(1)设乙距山脚的垂直高度 y与x之间的函数关系式为y= kx+b,
因为直线过(15,0)和(40,300),所以15k+b=0,40k+b=300,解得k=12,b=-180,
所以乙距山脚的垂直高度 y与x之间的函数关系式为y=12x-180;
(2)当 25≤x≤60时,设甲的函数表达式为y= mx+n,
将(25,160)和(60,300)代入,得160=25m+n,300=60m+n,解得m=4,n=60,所以y=4x+60;
因为乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度相等,所以12x-180=4x+60,解得. 所以
所以乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度为180 米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
