第六章 一次函数 综合测试卷(含答案)
文档属性
| 名称 | 第六章 一次函数 综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第六章综合测试卷
时间: 45分钟 满分: 100分
一、选择题(每题3分,共30分)
1.如图所示的图象分别给出了x与y的对应关系,其中表示y不是x的函数的是 ( )
2.一次函数的函数值 y随x的增大而减小,当 时,y的值可以是 ( )
A. 2 B. 1 C. -1 D. -2
3.下列函数象中,能反映y的值始终随x值的增大而增大的是 ( )
4.如图,在同一平面直角坐标系中,一次函数 与 的图象分别为直线 和直线 ,下列结论正确的是 ( )
5.已知:将直线y=x-1向上平移2个单位长度后得到直线,则下列关于直线的说法正确的是 ( )
A.经过第一、二、四象限 B.与x轴交于(1,0)
C.与y轴交于(0,1) D. y随x的增大而减小
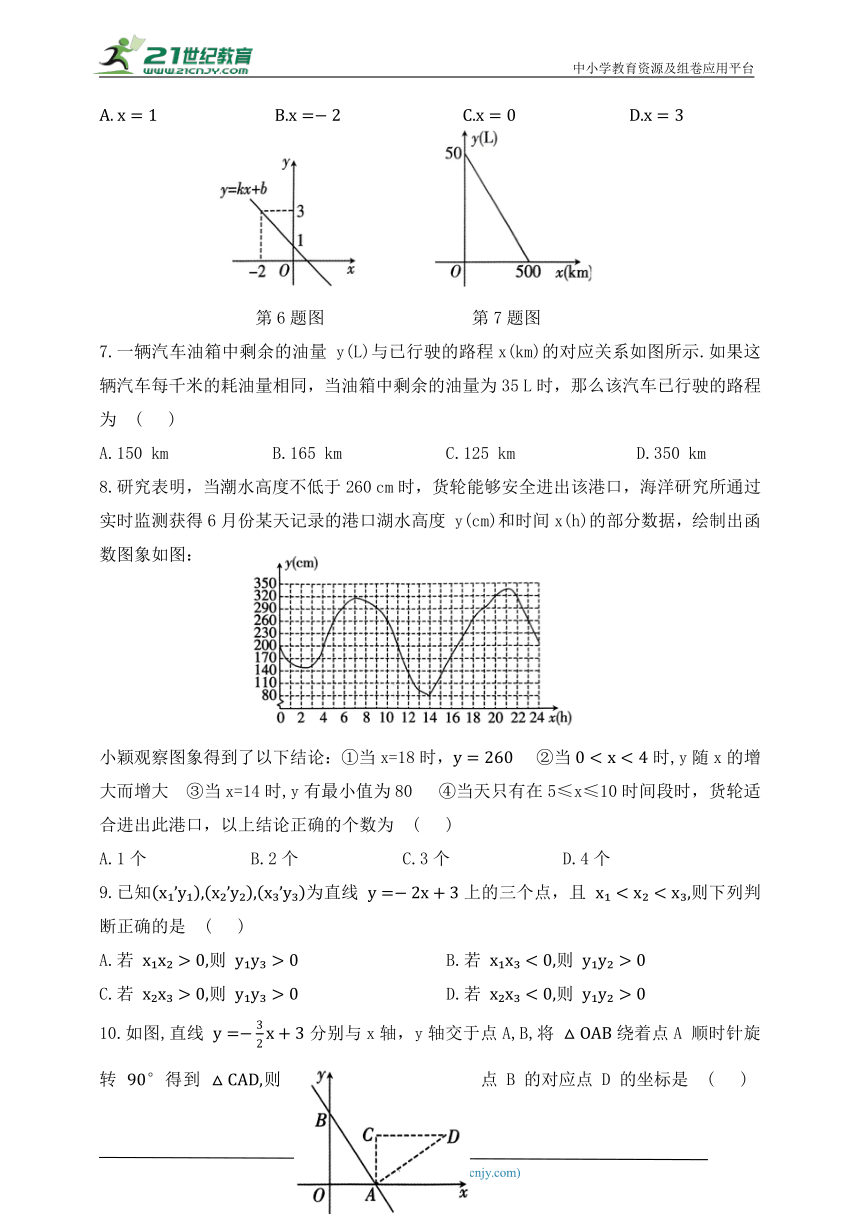
6.函数 的图象如图所示,根据图象信息可求得关于x 的方程 的解为 ( )
第6题图 第7题图
7.一辆汽车油箱中剩余的油量 y(L)与已行驶的路程x(km)的对应关系如图所示.如果这辆汽车每千米的耗油量相同,当油箱中剩余的油量为35 L时,那么该汽车已行驶的路程为 ( )
A.150 km B.165 km C.125 km D.350 km
8.研究表明,当潮水高度不低于260 cm时,货轮能够安全进出该港口,海洋研究所通过实时监测获得6月份某天记录的港口湖水高度 y(cm)和时间x(h)的部分数据,绘制出函数图象如图:
小颖观察图象得到了以下结论:①当x=18时,②当时,y随x的增大而增大 ③当x=14时,y有最小值为80 ④当天只有在5≤x≤10时间段时,货轮适合进出此港口,以上结论正确的个数为 ( )
A.1个 B.2个 C.3个 D.4个
9.已知为直线 上的三个点,且 则下列判断正确的是 ( )
A.若 则 B.若 则
C.若 则 D.若 则
10.如图,直线 分别与x轴,y轴交于点A,B,将 绕着点A 顺时针旋转 得到 则点 B 的对应点 D 的坐标是 ( )
A.(2,5) B.(3,5) C.(5,2)
二、填空题(每题 4分,共24分)
11.当_________ 时,函数 是正比例函数.
12.若一次函数的图象与直线 平行,且过点(0,2),则此一次函数的表达式是______________.
13.如图,已知一次函数 和正 比例函数的图象交于点 P(1,3),则关于
x的一元一次方程的解为____________.
14.若一次函数 的图象经过第一、二、四象限,则实数k的取值范围为_____________.
15.如图1,在 中, 动点P从点A 出发,沿折线A-B-C运动到点C,速度为2cm/s,其中 BP 的长与运动时间t 的关系如图2,则 的面积为____________
16.如图,甲、乙两人以相同的路线前往距离单位 10 km的培训中心参加学习,图中 分别表示甲、乙两人前往目的地所走的路程s(千米)随时间 t(分)变化的函数图象,以下说法中正确的是____________.(填序号)
①乙比甲提前12分钟到达 ②甲平均速度为0.25 千米/分钟
③甲、乙相遇时,乙走了6千米 ④乙出发6分钟后追上甲
三、解答题(共46分)
17.(10分)已知一次函数
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A 的坐标,与y轴的交点B 的坐标;
(3)在(2)条件下,求 的面积.
18.(12 分)如图,直线l的表达式为 它与坐标轴分别交于A,B两点.
(1)求出点 A 的坐标;
(2)动点C从y轴上的点(0,12)出发,以每秒1个单位长度的速度向 y轴负半轴运动,求出点 C运动的时间t,使得 为等腰三角形.
19.(12分)某加油站推出促销活动,一张加油卡的面值是1000元,打九折出售.使用这张加油卡加油,每一升油,油的单价降低0.30元.假设这张加油卡的面值能够一次性全部用完.
(1)他实际花了多少钱购买会员卡
(2)减价后每升油的单价为y元/升,原价为x元/升,求y关于x的函数表达式.
(3)油的原价是7.30元/升,求优惠后油的单价比原价便宜多少元
20.(12分)一辆巡逻车从 A 地出发沿一条笔直的公路匀速驶向 B 地, 小时后,一辆货车从 A 地出发,沿同一路线每小时行驶 80 千米匀速驶向 B 地,货车到达 B 地填装货物耗时15分钟,然后立即按原路匀速返回A 地.巡逻车、货车离A 地的距离y(千米)与货车出发时间x(小时)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A,B两地之间的距离是 _________千米,
(2)求线段 FG所在直线的函数表达式;
(3)货车出发多少小时两车相距15千米 (直接写出答案即可)
参考答案
1. A 2. D 3. C 4. D 5. C 6. A 7. A
8. B 解析:观察图象可知,
①当x=18时,y=260,说法正确;
②当0③当x=14时,y有最小值为80,说法正确;
④当天在5≤x≤10 以及18≤x≤23 时间段时,货轮适合进出此港口,原说法错误,所以结论正确的个数为2个.
9. D
10. C 解析:当x=0时, 则 B 点坐标为(0,3);
当y=0时, 解得x=2,则 A点坐标为(2,0),则OA=2,OB=3,
因为△AOB 绕点 A 顺时针旋转 90°后得到△ACD,
所以∠OAC=90°,∠ACD=∠AOB=90°,AC=AO=2,CD=OB=3,即AC⊥x轴,CD∥x轴,
所以点 D 的坐标为(5,2).
11.-2 13.
15.48 解析:当 时,点P 与点 A 重合,则
当 时,所以
过点A作 于点 D.
则
在 中,
所以
16.①②③④ 解析:①乙在 28分时到达,甲在40分时到达,所以乙比甲提前了12分钟到达,故①正确;②根据甲到达目的地时的路程和时间知甲的平均速度 (千米/分钟),故②正确;④设乙出发x分钟后追上甲,则有 解得 故④正确;③由④知:乙遇到甲时,所走的距离为故③正确.所以正确的结论有四个:①②③④.
17.解:(1)函数的图象如图所示,
(2)当 时, 当 时, 所以A(-2,0),B(0,4);
(3)因为 A(-2,0),B(0,4),所以OA=2,OB=4,所以
18.解:(1)令 y=0,则 解得x=3,则点 A 的坐标为(3,0);
(2)令x=0,则 则点 B 的坐标为(0,4),
①当 时,若点 C在点 B 上方时,如图1所示,
(秒);
若点 C在点 B 下方时,如图2所示,
(秒);
②当 时,如图3所示,
设 则
在 中, 所以
解得 (秒);
③当 时,如图4所示:
因为 AO⊥BC,所以OB=OC=4.t=(12+4)÷1=16(秒).
综上所述,当点 C运动的时间t 是 3 秒或13秒或 秒或 16 秒时,△ABC 为等腰三角形.
19.解:(1)由题意知,1000×0.9=900(元),答:实际花了 900 元购买会员卡;
(2)由题意知,y=0.9(x-0.30),整理得y=0.9x-0.27,
所以y关于x 的函数表达式为 y=0.9x-0.27;
(3)当x=7.30时, y=0.9×7.30-0.27=6.30,
因为7.30-6.30=1.00,所以优惠后油的单价比原价便宜1.00元.
20.解:(1)因为 (千米),所以A,B两地之间的距离是 60千米;
因为货车到达 B 地填装货物耗时15分钟,所以 故答案为:60,1;
(2)设线段 FG所在直线的表达式为 将F(1,60),G(2,0)代入得
解得
所以线段 FG所在直线的函数表达式为
(3)巡逻车速度为 (千米/时),
所以线段 CD 的表达式为
当货车第一次追上巡逻车后,解得
当货车返回与巡逻车未相遇时,解得
当货车返回与巡逻车相遇后, 解得
综上所述,货车出发 小时或 小时或 小时,两车相距15千米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章综合测试卷
时间: 45分钟 满分: 100分
一、选择题(每题3分,共30分)
1.如图所示的图象分别给出了x与y的对应关系,其中表示y不是x的函数的是 ( )
2.一次函数的函数值 y随x的增大而减小,当 时,y的值可以是 ( )
A. 2 B. 1 C. -1 D. -2
3.下列函数象中,能反映y的值始终随x值的增大而增大的是 ( )
4.如图,在同一平面直角坐标系中,一次函数 与 的图象分别为直线 和直线 ,下列结论正确的是 ( )
5.已知:将直线y=x-1向上平移2个单位长度后得到直线,则下列关于直线的说法正确的是 ( )
A.经过第一、二、四象限 B.与x轴交于(1,0)
C.与y轴交于(0,1) D. y随x的增大而减小
6.函数 的图象如图所示,根据图象信息可求得关于x 的方程 的解为 ( )
第6题图 第7题图
7.一辆汽车油箱中剩余的油量 y(L)与已行驶的路程x(km)的对应关系如图所示.如果这辆汽车每千米的耗油量相同,当油箱中剩余的油量为35 L时,那么该汽车已行驶的路程为 ( )
A.150 km B.165 km C.125 km D.350 km
8.研究表明,当潮水高度不低于260 cm时,货轮能够安全进出该港口,海洋研究所通过实时监测获得6月份某天记录的港口湖水高度 y(cm)和时间x(h)的部分数据,绘制出函数图象如图:
小颖观察图象得到了以下结论:①当x=18时,②当时,y随x的增大而增大 ③当x=14时,y有最小值为80 ④当天只有在5≤x≤10时间段时,货轮适合进出此港口,以上结论正确的个数为 ( )
A.1个 B.2个 C.3个 D.4个
9.已知为直线 上的三个点,且 则下列判断正确的是 ( )
A.若 则 B.若 则
C.若 则 D.若 则
10.如图,直线 分别与x轴,y轴交于点A,B,将 绕着点A 顺时针旋转 得到 则点 B 的对应点 D 的坐标是 ( )
A.(2,5) B.(3,5) C.(5,2)
二、填空题(每题 4分,共24分)
11.当_________ 时,函数 是正比例函数.
12.若一次函数的图象与直线 平行,且过点(0,2),则此一次函数的表达式是______________.
13.如图,已知一次函数 和正 比例函数的图象交于点 P(1,3),则关于
x的一元一次方程的解为____________.
14.若一次函数 的图象经过第一、二、四象限,则实数k的取值范围为_____________.
15.如图1,在 中, 动点P从点A 出发,沿折线A-B-C运动到点C,速度为2cm/s,其中 BP 的长与运动时间t 的关系如图2,则 的面积为____________
16.如图,甲、乙两人以相同的路线前往距离单位 10 km的培训中心参加学习,图中 分别表示甲、乙两人前往目的地所走的路程s(千米)随时间 t(分)变化的函数图象,以下说法中正确的是____________.(填序号)
①乙比甲提前12分钟到达 ②甲平均速度为0.25 千米/分钟
③甲、乙相遇时,乙走了6千米 ④乙出发6分钟后追上甲
三、解答题(共46分)
17.(10分)已知一次函数
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A 的坐标,与y轴的交点B 的坐标;
(3)在(2)条件下,求 的面积.
18.(12 分)如图,直线l的表达式为 它与坐标轴分别交于A,B两点.
(1)求出点 A 的坐标;
(2)动点C从y轴上的点(0,12)出发,以每秒1个单位长度的速度向 y轴负半轴运动,求出点 C运动的时间t,使得 为等腰三角形.
19.(12分)某加油站推出促销活动,一张加油卡的面值是1000元,打九折出售.使用这张加油卡加油,每一升油,油的单价降低0.30元.假设这张加油卡的面值能够一次性全部用完.
(1)他实际花了多少钱购买会员卡
(2)减价后每升油的单价为y元/升,原价为x元/升,求y关于x的函数表达式.
(3)油的原价是7.30元/升,求优惠后油的单价比原价便宜多少元
20.(12分)一辆巡逻车从 A 地出发沿一条笔直的公路匀速驶向 B 地, 小时后,一辆货车从 A 地出发,沿同一路线每小时行驶 80 千米匀速驶向 B 地,货车到达 B 地填装货物耗时15分钟,然后立即按原路匀速返回A 地.巡逻车、货车离A 地的距离y(千米)与货车出发时间x(小时)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A,B两地之间的距离是 _________千米,
(2)求线段 FG所在直线的函数表达式;
(3)货车出发多少小时两车相距15千米 (直接写出答案即可)
参考答案
1. A 2. D 3. C 4. D 5. C 6. A 7. A
8. B 解析:观察图象可知,
①当x=18时,y=260,说法正确;
②当0
④当天在5≤x≤10 以及18≤x≤23 时间段时,货轮适合进出此港口,原说法错误,所以结论正确的个数为2个.
9. D
10. C 解析:当x=0时, 则 B 点坐标为(0,3);
当y=0时, 解得x=2,则 A点坐标为(2,0),则OA=2,OB=3,
因为△AOB 绕点 A 顺时针旋转 90°后得到△ACD,
所以∠OAC=90°,∠ACD=∠AOB=90°,AC=AO=2,CD=OB=3,即AC⊥x轴,CD∥x轴,
所以点 D 的坐标为(5,2).
11.-2 13.
15.48 解析:当 时,点P 与点 A 重合,则
当 时,所以
过点A作 于点 D.
则
在 中,
所以
16.①②③④ 解析:①乙在 28分时到达,甲在40分时到达,所以乙比甲提前了12分钟到达,故①正确;②根据甲到达目的地时的路程和时间知甲的平均速度 (千米/分钟),故②正确;④设乙出发x分钟后追上甲,则有 解得 故④正确;③由④知:乙遇到甲时,所走的距离为故③正确.所以正确的结论有四个:①②③④.
17.解:(1)函数的图象如图所示,
(2)当 时, 当 时, 所以A(-2,0),B(0,4);
(3)因为 A(-2,0),B(0,4),所以OA=2,OB=4,所以
18.解:(1)令 y=0,则 解得x=3,则点 A 的坐标为(3,0);
(2)令x=0,则 则点 B 的坐标为(0,4),
①当 时,若点 C在点 B 上方时,如图1所示,
(秒);
若点 C在点 B 下方时,如图2所示,
(秒);
②当 时,如图3所示,
设 则
在 中, 所以
解得 (秒);
③当 时,如图4所示:
因为 AO⊥BC,所以OB=OC=4.t=(12+4)÷1=16(秒).
综上所述,当点 C运动的时间t 是 3 秒或13秒或 秒或 16 秒时,△ABC 为等腰三角形.
19.解:(1)由题意知,1000×0.9=900(元),答:实际花了 900 元购买会员卡;
(2)由题意知,y=0.9(x-0.30),整理得y=0.9x-0.27,
所以y关于x 的函数表达式为 y=0.9x-0.27;
(3)当x=7.30时, y=0.9×7.30-0.27=6.30,
因为7.30-6.30=1.00,所以优惠后油的单价比原价便宜1.00元.
20.解:(1)因为 (千米),所以A,B两地之间的距离是 60千米;
因为货车到达 B 地填装货物耗时15分钟,所以 故答案为:60,1;
(2)设线段 FG所在直线的表达式为 将F(1,60),G(2,0)代入得
解得
所以线段 FG所在直线的函数表达式为
(3)巡逻车速度为 (千米/时),
所以线段 CD 的表达式为
当货车第一次追上巡逻车后,解得
当货车返回与巡逻车未相遇时,解得
当货车返回与巡逻车相遇后, 解得
综上所述,货车出发 小时或 小时或 小时,两车相距15千米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
