2025高考物理二轮复习专题一-力与运动-第1讲 物体的平衡(共36张PPT)
文档属性
| 名称 | 2025高考物理二轮复习专题一-力与运动-第1讲 物体的平衡(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-29 10:55:08 | ||
图片预览










文档简介
(共36张PPT)
第1讲 物体的平衡
题型1 静态平衡问题
题型2 动态平衡问题
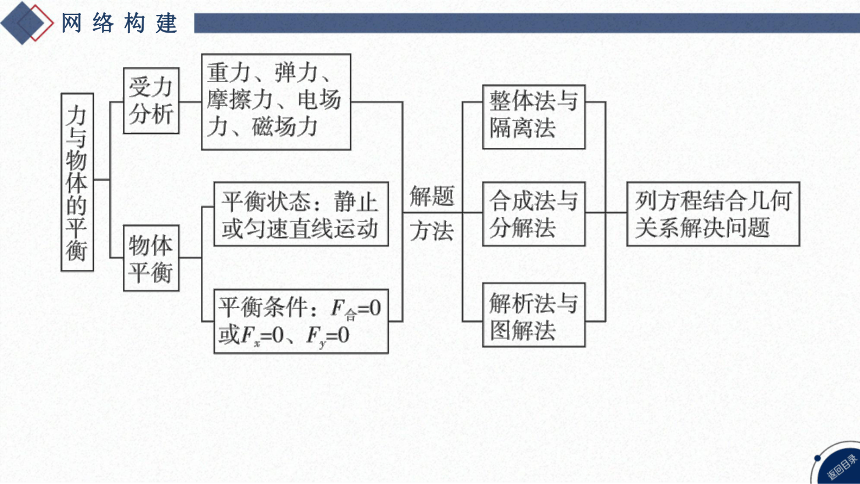
网络构建
备用习题
【关键能力】
理解力和力的运算法则,会正确受力分析,熟练运用力的平衡的各种表达形
式.灵活选取研究对象、会根据实际情况构建平衡模型,同时掌握临界法、
函数法、图像法、整体法、隔离法等解题方法,联系生活实际,培养学生的
物理观念和科学思维.
题型1 静态平衡问题
例1 [2024·浙江1月选考] 如图所示,在同一竖直
平面内,小球、上系有不可伸长的细线 、
、和,其中 的上端悬挂于竖直固定的支架
上,跨过左侧定滑轮、 跨过右侧定滑轮分别与
相同配重、 相连,调节左、右两侧定滑轮高度
达到平衡.已知小球、和配重、 质量均为
A.、 B.、 C.、 D.、
,细线、平行且与水平面成 角 不计摩擦,取 ,
则细线、 的拉力分别为( )
√
[解析] 对A、B整体受力分析,如图甲所示,根据平衡条件可知 ;对B球受力分析,设与水平方向夹角为 ,如图乙所示,根据平衡条件可知 , ,联立解得 , ,选项D正确.
甲
乙
技法点拨
定滑轮只改变力的方向,不改变力的大小,在分析细绳
用整体受力分析;当分析
也可以对
例2 [2020·浙江1月选考] 如图所示,在倾角为
的光滑绝缘斜面上固定一个挡板,在挡板上连接
一根劲度系数为 的绝缘轻质弹簧,弹簧另一端
A. B.弹簧伸长量为
C.球受到的库仑力大小为 D.相邻两小球间距为
与球连接.、、三小球的质量均为,, ,当系
统处于静止状态时,三小球等间距排列.已知静电力常量为 ,重力加速度
为 ,则( )
√
[解析] 假设小球C带负电,相邻两小球间距为 ,
对小球C受力分析如图甲所示,根据库仑定律有
, ,显然小球C无法处于静
止,因此小球C应该带正电,根据平衡条件得
, 则 ,
对B球受力分析如图乙所示,根据平衡条件得
,联立解得 ,
甲
乙
,选项A正确,
D错误.A所受B、C的库仑力的合力为
,方向
沿斜面向下,选项C错误.将三个小球看作整体分
析,受到重力、支持力、
弹簧弹力,根据平衡条件得 ,弹簧
伸长量为 ,
选项B错误.
甲
乙
技法点拨
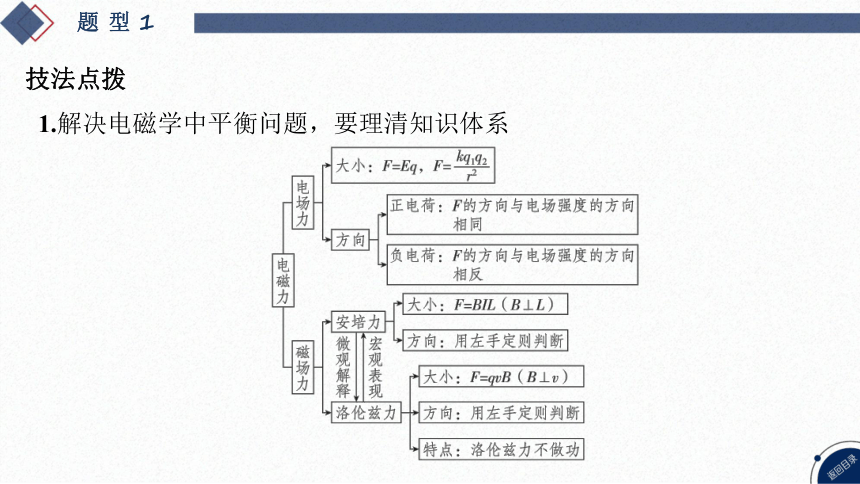
1.解决电磁学中平衡问题,要理清知识体系
2.本例在分析球时,采用假设法结合平衡知识进行讨论,也可以先求 处
电场方向,电场力又必须沿斜面向上,从而求得 球电性.与电场力相关的
平衡问题可以直接用电场力分析,也可以通过电场强度进行分析.
【迁移拓展】
1.[2022·浙江1月选考] 如图所示,学校门口水平地面上有一质量为 的石
墩,石墩与水平地面间的动摩擦因数为 ,工作人员用轻绳按图示方式匀
速移动石墩时,两平行轻绳与水平面间的夹角均为 ,重力加速度为 ,
则下列说法正确的是( )
A.轻绳的合拉力大小为
B.轻绳的合拉力大小为
C.减小夹角 ,轻绳的合拉力一定减小
D.轻绳的合拉力最小时,地面对石墩的摩擦力也最小
√
[解析] 对石墩受力分析,如图所示,设
两根轻绳的拉力均为 ,根据平衡条件,
有, ,
且, ,联立解得
,选项A错误,B正确;
,其中
,,即 是一个常数,
根据三角函数知识知,减小夹角 ,
可能减小,轻绳的合拉力
可能增大,选项C错误;根据 的表达式
可知,当 时,合拉力最小,而
摩擦力
,当
时,摩擦力最小,即合拉力最小和
摩擦力最小对应的 取值不同,所以合
拉力最小时,摩擦力不是最小,选项D
错误.
2.[2024·温州模拟] 如图所示,质量为、半径为 的圆环状光滑绝缘细杆
用三根交于 点的等长细线悬挂于水平面内,每根细线与竖直方向均成
角,杆上套有三个可视为质点的带正电小球,每个小球的质量均为 、
电荷量均为,小球间的距离相等,球和杆均静止.重力加速度大小为 ,
静电力常量为 ,则( )
A.每根细线对杆的拉力大小为
B.每根细线对杆的拉力大小为
C.每个小球受到的库仑力大小为
D.每个小球对杆的弹力大小为
√
[解析] 对杆和小球整体受力分析,竖直方向上有
,
解得每根细线对杆的拉力大小为 ,
故A、B错误;根据
题意可得,两个小球间的距离为 ,所
以每个小球受到的库
仑力大小为 ,故C错误;
每个小球对杆的弹力大
小为 ,故D正确.
题型2 动态平衡问题
1.动态平衡:通过控制某些物理量,使物体的状态发生缓慢的变化,而在这个
过程中物体又始终处于一系列的平衡状态,在问题的描述中常用“缓慢”等语
言叙述.
2.做题流程
例3 如图所示,在竖直放置的穹形支架上,一根长度不
变且不可伸长的轻绳通过轻质光滑滑轮悬挂一重物 .现
将轻绳的一端固定于支架上的点,另一端从 点沿支
架缓慢地向点靠近点与点等高 ,则在此过程中绳
中拉力大小( )
A.先变大后不变 B.先变大后变小 C.先变小后不变 D.先变小后变大
√
[解析] 对滑轮受力分析如图甲所示,由于跨过滑轮的绳子两端拉力大小一定相等,即 ,由几何关系可知绳子两端拉力方向与竖直方向的夹角相等,设为 ,可知,如图乙所示,设绳长为 ,由几何关系可知,其中 为绳子两端点间的水平距离,轻绳另一端由B点向C点移动过程中, 先变大后不变,因此 先变大后不变,可知绳中拉力先变大后不变,故A正确.
技法点拨
破解动态平衡问题
例4 [2024·衢州模拟] 如图所示,用轻质网兜将一质量均匀的足球悬挂在竖直木板的点,轻绳与木板之间的夹角为 .将木板以底端为轴顺时针缓慢转动直至木板水平,转动过程中绳与木板之间的夹角保持不变.忽略一切摩擦,球的重力为 .设木板对球的支持力为,绳上的拉力为 ,在木板转动过程中,下列说法正确的是( )
A.的最小值为
B.的最大值为
C.当木板转动 时,是 大小的三倍
D.当木板转动 时,与 大小相等
√
[解析] 在木板转动过程中,足球的受力如图所示,
根据正弦定理可得 ,其中
保持不变, 由 逐渐减小到0,
从锐角逐渐增大到钝角,则 保持不
变, 逐渐减小, 先增大后减小,可知
悬绳对足球的拉力 逐渐减小,木板对足球的支
持力先增大后减小.初始状态时 最小,为
,A错误;当木板转动
时, , ,此时 最大,为
,此时,则
是大小的2倍,B、C错误;当木板转动
时, , ,、、 三力构成
的矢量三角形为等边三角形,与 大小相等,
D正确.
【迁移拓展】
1.如图所示,用、 两根轻绳将花盆悬于两竖直墙之间.
开始时绳水平,现保持点位置不变,改变 绳长,使
绳右端由点缓慢上移至点,此时与 之间的夹角
.设此过程中、绳的拉力分别为、 ,则
下列说法正确的是( )
A.一直减小 B. 先减小后增大
C.一直增大 D. 一直减小
√
[解析] 根据题意,以花盆为研究对象,分析受力,受重力、绳 的拉
力和绳的拉力 ,根据平衡条件知,两根绳子的拉力的合力与重
力大小相等、方向相反,作出轻绳 在不同位置时力的合成图,如图所
示,由图可看出,逐渐减小,先减小后增大,当 时,
最小,故A正确,B、C、D错误.
2.如图所示,光滑绝缘圆环轨道竖直固定,两个质量均为 、带等量同种
电荷的小环、套在圆环轨道上.小环固定在轨道最低点,初始时 处于
静止状态,、之间距离为小于轨道直径的长度.小环 缓慢漏电,自
图示位置开始缓慢下滑,则( )
A.小环 对轨道的压力可能先指向圆心,后背离圆心
B.小环 对轨道的压力大小始终不变
C.两小环之间的库仑力先增大后减小
D.当小环的电荷量减为初始电荷量的一半时,、
之间的距离也减半
√
[解析] 对小环 进行受力分析,如图所示,将轨道
对小环的支持力和两小环之间的库仑力 平移构
成矢量三角形,设圆环轨道的半径为 ,两环之间
的距离为 ,根据相似三角形的特点可得
,解得,,当小环 缓
慢漏电时,从图示位置开始缓慢下滑,则减小,
减小, 大小不变,即库仑力不断减小,轨道对小
环 的支持力大小不变,方向始终指向圆心,由牛
顿第三定律可知,小环 对轨道的压力大小始终不
变,且方向始终背离圆心,故A、C错误,B正确;
设、的初始带电荷量大小均为 ,在最初的位置
时,根据库仑定律可得,当小环 的电荷量
减为初始电荷量的一半时,假设、 之间的距离也
减半,则此时的库仑力大小为 ,这与整个过程中库仑力
在不断减小相矛盾,说明假设错误,故D错误.
1. 冰雪运动爱好者利用无人机牵引,在光滑水平冰面上匀速滑行,如图所示.牵引绳与竖直方向成θ角,人所受的空气阻力恒定.下列说法正确的是 ( )
A.θ越大,则绳子对人的拉力越大
B.θ越大,则冰面对人的支持力越大
C.空气对无人机的作用力可能沿着绳子方向
D.无人机对绳的拉力与绳对人的拉力是一对相互作用力
√
[解析] 以人为研究对象,受力分析如图所示,根据平衡条件,可得水平方向上有F阻=FTsin θ,竖直方向上有FTcos θ+FN=mg,可得FN=mg-FTcos θ,FT=,人所受的空气阻力F阻恒定,θ越大,则绳子对人的拉力FT越小,冰面对人的支持力FN越大,故B正确,A错误;
以无人机为研究对象,无人机受到空气的作用力、绳子拉力和重力,由平衡条件可知,空气对无人机的作用力与无人机的重力和绳子拉力的合力等大反向,不可能沿着绳子方向,故C错误;
一对相互作用力只涉及两个物体,无人机对绳的拉力与绳
对人的拉力这对力涉及三个物体,一定不是一对相互作用力,故D错误.
2. 如图所示,用两根等长的细绳将一匀质圆柱体悬挂在竖直木板的P点,将木板以底边MN为轴向后方缓慢转动直至水平,绳与木板之间的夹角保持不变,忽略圆柱体与木板之间的摩擦,在转动过程中 ( )
A.圆柱体对木板的压力逐渐增大
B.圆柱体对木板的压力先增大后减小
C.两根细绳上的拉力均先增大后减小
D.两根细绳对圆柱体拉力的合力保持不变
√
[解析] 在转动过程中,绳与木板之间的夹角保持不变,则两绳对圆柱体的拉力的合力与木板对圆柱体的支持力的夹角不变.设绳子拉力为FT,两绳子之间的夹角为2θ,两绳子对圆柱体的拉力的合力为F,则2FTcos θ=F,可得FT=.对圆柱体受力分析,画出力的矢量三角形,如图所示,G为圆柱体的重力,FN为圆柱体所受的支持力.因为G的大小和方向不变,F和FN的夹角保持不变,所以任意时刻对应的矢量三角形都处于同一个外接圆中.在将木板以底边MN为轴向后方缓慢转动直至水平过程中,由图可判断出FN先增大后减小,F逐渐减小,进而推出FT不断减小,由牛顿第三定律可知,圆柱体对木板的
压力先增大后减小,B正确,A、C、D错误.
第1讲 物体的平衡
题型1 静态平衡问题
题型2 动态平衡问题
网络构建
备用习题
【关键能力】
理解力和力的运算法则,会正确受力分析,熟练运用力的平衡的各种表达形
式.灵活选取研究对象、会根据实际情况构建平衡模型,同时掌握临界法、
函数法、图像法、整体法、隔离法等解题方法,联系生活实际,培养学生的
物理观念和科学思维.
题型1 静态平衡问题
例1 [2024·浙江1月选考] 如图所示,在同一竖直
平面内,小球、上系有不可伸长的细线 、
、和,其中 的上端悬挂于竖直固定的支架
上,跨过左侧定滑轮、 跨过右侧定滑轮分别与
相同配重、 相连,调节左、右两侧定滑轮高度
达到平衡.已知小球、和配重、 质量均为
A.、 B.、 C.、 D.、
,细线、平行且与水平面成 角 不计摩擦,取 ,
则细线、 的拉力分别为( )
√
[解析] 对A、B整体受力分析,如图甲所示,根据平衡条件可知 ;对B球受力分析,设与水平方向夹角为 ,如图乙所示,根据平衡条件可知 , ,联立解得 , ,选项D正确.
甲
乙
技法点拨
定滑轮只改变力的方向,不改变力的大小,在分析细绳
用整体受力分析;当分析
也可以对
例2 [2020·浙江1月选考] 如图所示,在倾角为
的光滑绝缘斜面上固定一个挡板,在挡板上连接
一根劲度系数为 的绝缘轻质弹簧,弹簧另一端
A. B.弹簧伸长量为
C.球受到的库仑力大小为 D.相邻两小球间距为
与球连接.、、三小球的质量均为,, ,当系
统处于静止状态时,三小球等间距排列.已知静电力常量为 ,重力加速度
为 ,则( )
√
[解析] 假设小球C带负电,相邻两小球间距为 ,
对小球C受力分析如图甲所示,根据库仑定律有
, ,显然小球C无法处于静
止,因此小球C应该带正电,根据平衡条件得
, 则 ,
对B球受力分析如图乙所示,根据平衡条件得
,联立解得 ,
甲
乙
,选项A正确,
D错误.A所受B、C的库仑力的合力为
,方向
沿斜面向下,选项C错误.将三个小球看作整体分
析,受到重力、支持力、
弹簧弹力,根据平衡条件得 ,弹簧
伸长量为 ,
选项B错误.
甲
乙
技法点拨
1.解决电磁学中平衡问题,要理清知识体系
2.本例在分析球时,采用假设法结合平衡知识进行讨论,也可以先求 处
电场方向,电场力又必须沿斜面向上,从而求得 球电性.与电场力相关的
平衡问题可以直接用电场力分析,也可以通过电场强度进行分析.
【迁移拓展】
1.[2022·浙江1月选考] 如图所示,学校门口水平地面上有一质量为 的石
墩,石墩与水平地面间的动摩擦因数为 ,工作人员用轻绳按图示方式匀
速移动石墩时,两平行轻绳与水平面间的夹角均为 ,重力加速度为 ,
则下列说法正确的是( )
A.轻绳的合拉力大小为
B.轻绳的合拉力大小为
C.减小夹角 ,轻绳的合拉力一定减小
D.轻绳的合拉力最小时,地面对石墩的摩擦力也最小
√
[解析] 对石墩受力分析,如图所示,设
两根轻绳的拉力均为 ,根据平衡条件,
有, ,
且, ,联立解得
,选项A错误,B正确;
,其中
,,即 是一个常数,
根据三角函数知识知,减小夹角 ,
可能减小,轻绳的合拉力
可能增大,选项C错误;根据 的表达式
可知,当 时,合拉力最小,而
摩擦力
,当
时,摩擦力最小,即合拉力最小和
摩擦力最小对应的 取值不同,所以合
拉力最小时,摩擦力不是最小,选项D
错误.
2.[2024·温州模拟] 如图所示,质量为、半径为 的圆环状光滑绝缘细杆
用三根交于 点的等长细线悬挂于水平面内,每根细线与竖直方向均成
角,杆上套有三个可视为质点的带正电小球,每个小球的质量均为 、
电荷量均为,小球间的距离相等,球和杆均静止.重力加速度大小为 ,
静电力常量为 ,则( )
A.每根细线对杆的拉力大小为
B.每根细线对杆的拉力大小为
C.每个小球受到的库仑力大小为
D.每个小球对杆的弹力大小为
√
[解析] 对杆和小球整体受力分析,竖直方向上有
,
解得每根细线对杆的拉力大小为 ,
故A、B错误;根据
题意可得,两个小球间的距离为 ,所
以每个小球受到的库
仑力大小为 ,故C错误;
每个小球对杆的弹力大
小为 ,故D正确.
题型2 动态平衡问题
1.动态平衡:通过控制某些物理量,使物体的状态发生缓慢的变化,而在这个
过程中物体又始终处于一系列的平衡状态,在问题的描述中常用“缓慢”等语
言叙述.
2.做题流程
例3 如图所示,在竖直放置的穹形支架上,一根长度不
变且不可伸长的轻绳通过轻质光滑滑轮悬挂一重物 .现
将轻绳的一端固定于支架上的点,另一端从 点沿支
架缓慢地向点靠近点与点等高 ,则在此过程中绳
中拉力大小( )
A.先变大后不变 B.先变大后变小 C.先变小后不变 D.先变小后变大
√
[解析] 对滑轮受力分析如图甲所示,由于跨过滑轮的绳子两端拉力大小一定相等,即 ,由几何关系可知绳子两端拉力方向与竖直方向的夹角相等,设为 ,可知,如图乙所示,设绳长为 ,由几何关系可知,其中 为绳子两端点间的水平距离,轻绳另一端由B点向C点移动过程中, 先变大后不变,因此 先变大后不变,可知绳中拉力先变大后不变,故A正确.
技法点拨
破解动态平衡问题
例4 [2024·衢州模拟] 如图所示,用轻质网兜将一质量均匀的足球悬挂在竖直木板的点,轻绳与木板之间的夹角为 .将木板以底端为轴顺时针缓慢转动直至木板水平,转动过程中绳与木板之间的夹角保持不变.忽略一切摩擦,球的重力为 .设木板对球的支持力为,绳上的拉力为 ,在木板转动过程中,下列说法正确的是( )
A.的最小值为
B.的最大值为
C.当木板转动 时,是 大小的三倍
D.当木板转动 时,与 大小相等
√
[解析] 在木板转动过程中,足球的受力如图所示,
根据正弦定理可得 ,其中
保持不变, 由 逐渐减小到0,
从锐角逐渐增大到钝角,则 保持不
变, 逐渐减小, 先增大后减小,可知
悬绳对足球的拉力 逐渐减小,木板对足球的支
持力先增大后减小.初始状态时 最小,为
,A错误;当木板转动
时, , ,此时 最大,为
,此时,则
是大小的2倍,B、C错误;当木板转动
时, , ,、、 三力构成
的矢量三角形为等边三角形,与 大小相等,
D正确.
【迁移拓展】
1.如图所示,用、 两根轻绳将花盆悬于两竖直墙之间.
开始时绳水平,现保持点位置不变,改变 绳长,使
绳右端由点缓慢上移至点,此时与 之间的夹角
.设此过程中、绳的拉力分别为、 ,则
下列说法正确的是( )
A.一直减小 B. 先减小后增大
C.一直增大 D. 一直减小
√
[解析] 根据题意,以花盆为研究对象,分析受力,受重力、绳 的拉
力和绳的拉力 ,根据平衡条件知,两根绳子的拉力的合力与重
力大小相等、方向相反,作出轻绳 在不同位置时力的合成图,如图所
示,由图可看出,逐渐减小,先减小后增大,当 时,
最小,故A正确,B、C、D错误.
2.如图所示,光滑绝缘圆环轨道竖直固定,两个质量均为 、带等量同种
电荷的小环、套在圆环轨道上.小环固定在轨道最低点,初始时 处于
静止状态,、之间距离为小于轨道直径的长度.小环 缓慢漏电,自
图示位置开始缓慢下滑,则( )
A.小环 对轨道的压力可能先指向圆心,后背离圆心
B.小环 对轨道的压力大小始终不变
C.两小环之间的库仑力先增大后减小
D.当小环的电荷量减为初始电荷量的一半时,、
之间的距离也减半
√
[解析] 对小环 进行受力分析,如图所示,将轨道
对小环的支持力和两小环之间的库仑力 平移构
成矢量三角形,设圆环轨道的半径为 ,两环之间
的距离为 ,根据相似三角形的特点可得
,解得,,当小环 缓
慢漏电时,从图示位置开始缓慢下滑,则减小,
减小, 大小不变,即库仑力不断减小,轨道对小
环 的支持力大小不变,方向始终指向圆心,由牛
顿第三定律可知,小环 对轨道的压力大小始终不
变,且方向始终背离圆心,故A、C错误,B正确;
设、的初始带电荷量大小均为 ,在最初的位置
时,根据库仑定律可得,当小环 的电荷量
减为初始电荷量的一半时,假设、 之间的距离也
减半,则此时的库仑力大小为 ,这与整个过程中库仑力
在不断减小相矛盾,说明假设错误,故D错误.
1. 冰雪运动爱好者利用无人机牵引,在光滑水平冰面上匀速滑行,如图所示.牵引绳与竖直方向成θ角,人所受的空气阻力恒定.下列说法正确的是 ( )
A.θ越大,则绳子对人的拉力越大
B.θ越大,则冰面对人的支持力越大
C.空气对无人机的作用力可能沿着绳子方向
D.无人机对绳的拉力与绳对人的拉力是一对相互作用力
√
[解析] 以人为研究对象,受力分析如图所示,根据平衡条件,可得水平方向上有F阻=FTsin θ,竖直方向上有FTcos θ+FN=mg,可得FN=mg-FTcos θ,FT=,人所受的空气阻力F阻恒定,θ越大,则绳子对人的拉力FT越小,冰面对人的支持力FN越大,故B正确,A错误;
以无人机为研究对象,无人机受到空气的作用力、绳子拉力和重力,由平衡条件可知,空气对无人机的作用力与无人机的重力和绳子拉力的合力等大反向,不可能沿着绳子方向,故C错误;
一对相互作用力只涉及两个物体,无人机对绳的拉力与绳
对人的拉力这对力涉及三个物体,一定不是一对相互作用力,故D错误.
2. 如图所示,用两根等长的细绳将一匀质圆柱体悬挂在竖直木板的P点,将木板以底边MN为轴向后方缓慢转动直至水平,绳与木板之间的夹角保持不变,忽略圆柱体与木板之间的摩擦,在转动过程中 ( )
A.圆柱体对木板的压力逐渐增大
B.圆柱体对木板的压力先增大后减小
C.两根细绳上的拉力均先增大后减小
D.两根细绳对圆柱体拉力的合力保持不变
√
[解析] 在转动过程中,绳与木板之间的夹角保持不变,则两绳对圆柱体的拉力的合力与木板对圆柱体的支持力的夹角不变.设绳子拉力为FT,两绳子之间的夹角为2θ,两绳子对圆柱体的拉力的合力为F,则2FTcos θ=F,可得FT=.对圆柱体受力分析,画出力的矢量三角形,如图所示,G为圆柱体的重力,FN为圆柱体所受的支持力.因为G的大小和方向不变,F和FN的夹角保持不变,所以任意时刻对应的矢量三角形都处于同一个外接圆中.在将木板以底边MN为轴向后方缓慢转动直至水平过程中,由图可判断出FN先增大后减小,F逐渐减小,进而推出FT不断减小,由牛顿第三定律可知,圆柱体对木板的
压力先增大后减小,B正确,A、C、D错误.
同课章节目录
