11.3.1单项式乘以多项式课件(18张PPT)
文档属性
| 名称 | 11.3.1单项式乘以多项式课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 797.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-11 00:00:00 | ||
图片预览






文档简介
课件18张PPT。第二课时
单项式乘以多项式
§11.3.2 单项式的乘法例1 先找出下列多项式中的同类项,然后合并同类项:(1)4x2-8x+5-3x2+6x-2; 原式=4x2-8x+5-3x2+6x-2====== ====== ~~~~ ~~~~=(4x2-3x2)+(-8x+6x)+(5-2)= x2-2x+3;解:(标出同类项)(结合同类项)(合并同类项)知识回顾一:单项式的乘法法则包括以下三部分:
(1)积的系数等于各因式系数的积;
(2)相同字母相乘;
(3)只在一个单项式里含有的字母,
要连同它的指数写在积里.(注意 不要把这个因式丢掉)有理数的乘法(同底数幂的乘法)
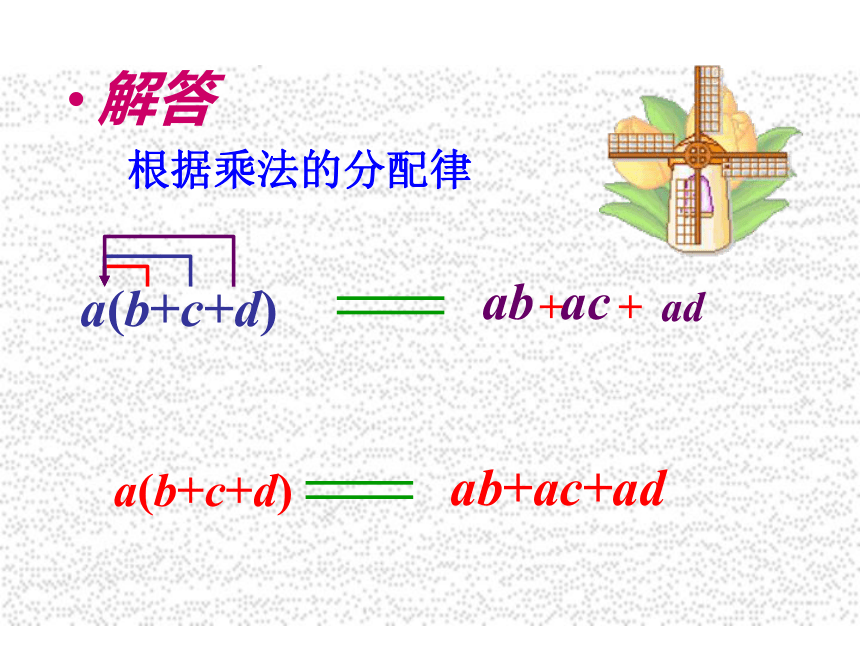
单项式与单项式相乘,把它们的系数、相同字母的 幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式. 单项式的乘法法则知识回顾21.根据单项式乘单项式的法则填空: 青云学府有一块如图所示的绿化区,分别种植了不同的植物,你知道绿化区的总面积吗?情景导航ab+ac+ada(b+c+d)=a(b+c+d)ac+adab+根据乘法的分配律解答 单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加.单项式乘多项式的运算法则结论~~~~ ~~~~例1 计算:(1) 单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加. 1.计算:
(1) (-3x2)·(4x-3)
(2) (4) 学以致用 (3)2:如图:一块长方形地用来建造住宅、广场、商厦,求这块地的面积.学以致用 3.填空(1)( )
(2)
(3)
(4)已知a2(2ax-3ay)=2a6-3a3,则x= ,y= .学以致用 4.化简:
其中y=-3,n=2.学以致用 解:去括号,得合并同类项,得系数化为1,得跟踪练习2:作业精编第44页的第15题(写纸上)1.已知:xy2=-2,求-xy(x3y7-3x2y5-y)2.思考: 若的结果中不含 知识延伸4.已知M,N分别表示不同的单项式,且3x(M-5x)=6x2y3+N,求M、N的值. 3.已知A=-3xy2,B=2xy(x-y),求A·B 知识延伸这节课你学会了什么? 1.单项式与多项式相乘的依据是乘法对加法的分配律.
2.单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数相同,注意不要漏乘项.
3.积的每一项的符号由原多项式各项符号和单项式的符号来决定,注意运用去括号法则.小结:学 海 无 涯驶向成功的彼岸长风破浪会有时直挂云帆济沧海 再 见
单项式乘以多项式
§11.3.2 单项式的乘法例1 先找出下列多项式中的同类项,然后合并同类项:(1)4x2-8x+5-3x2+6x-2; 原式=4x2-8x+5-3x2+6x-2====== ====== ~~~~ ~~~~=(4x2-3x2)+(-8x+6x)+(5-2)= x2-2x+3;解:(标出同类项)(结合同类项)(合并同类项)知识回顾一:单项式的乘法法则包括以下三部分:
(1)积的系数等于各因式系数的积;
(2)相同字母相乘;
(3)只在一个单项式里含有的字母,
要连同它的指数写在积里.(注意 不要把这个因式丢掉)有理数的乘法(同底数幂的乘法)
单项式与单项式相乘,把它们的系数、相同字母的 幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式. 单项式的乘法法则知识回顾21.根据单项式乘单项式的法则填空: 青云学府有一块如图所示的绿化区,分别种植了不同的植物,你知道绿化区的总面积吗?情景导航ab+ac+ada(b+c+d)=a(b+c+d)ac+adab+根据乘法的分配律解答 单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加.单项式乘多项式的运算法则结论~~~~ ~~~~例1 计算:(1) 单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加. 1.计算:
(1) (-3x2)·(4x-3)
(2) (4) 学以致用 (3)2:如图:一块长方形地用来建造住宅、广场、商厦,求这块地的面积.学以致用 3.填空(1)( )
(2)
(3)
(4)已知a2(2ax-3ay)=2a6-3a3,则x= ,y= .学以致用 4.化简:
其中y=-3,n=2.学以致用 解:去括号,得合并同类项,得系数化为1,得跟踪练习2:作业精编第44页的第15题(写纸上)1.已知:xy2=-2,求-xy(x3y7-3x2y5-y)2.思考: 若的结果中不含 知识延伸4.已知M,N分别表示不同的单项式,且3x(M-5x)=6x2y3+N,求M、N的值. 3.已知A=-3xy2,B=2xy(x-y),求A·B 知识延伸这节课你学会了什么? 1.单项式与多项式相乘的依据是乘法对加法的分配律.
2.单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数相同,注意不要漏乘项.
3.积的每一项的符号由原多项式各项符号和单项式的符号来决定,注意运用去括号法则.小结:学 海 无 涯驶向成功的彼岸长风破浪会有时直挂云帆济沧海 再 见
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
