1.1.2直角三角形的性质和判定 课件(共23张PPT)
文档属性
| 名称 | 1.1.2直角三角形的性质和判定 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
第一章 直角三角形
1.1.2直角三角形的性质和判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
掌握直角掌握直角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半”三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜掌握直角三角形的性掌握直角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直掌握直角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它
掌握直角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半”角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半”果一个锐角等于30度,那么它所对的直角边等于斜边的一半”边的一半”
01
02
03
体会从“一般到特殊”的思维方法和“逆向思维”方法,培养逆向思维能力.
掌握直角三角形的性质“直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30度”.
02
新知导入
思考:一个三角形应满足什么条件才能是直角三角形
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和是90°的三角形是直角三角形;
(3)一边上的中线等于这条边的一半的三角形是直角三角形。
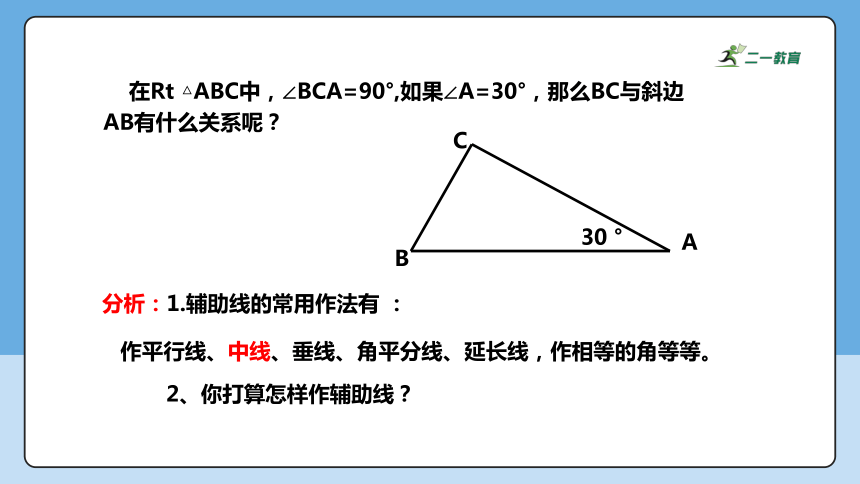
在Rt △ABC中,∠BCA=90°,如果∠A=30°,那么BC与斜边AB有什么关系呢?
分析:1.辅助线的常用作法有 :
30 °
B
C
A
作平行线、中线、垂线、角平分线、延长线,作相等的角等等。
2、你打算怎样作辅助线?
03
新知探究
D
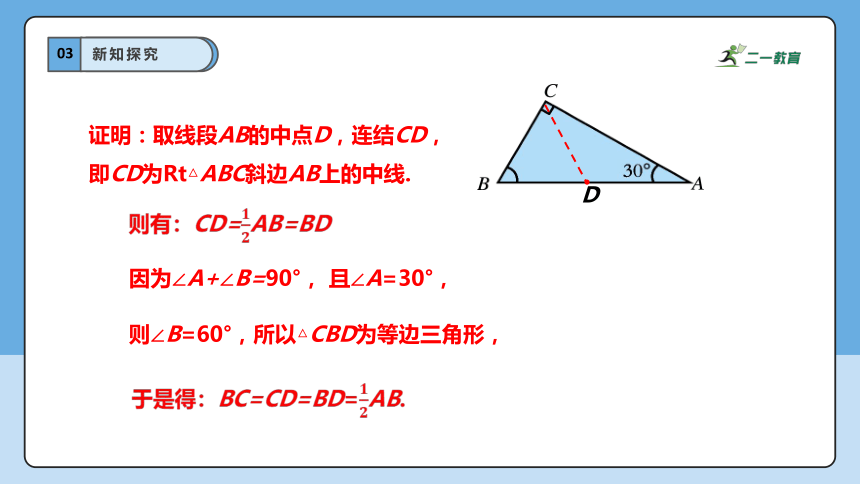
证明:取线段AB的中点D,连结CD,
即CD为Rt△ABC斜边AB上的中线.
则有:CD=AB=BD
因为∠A+∠B=90°, 且∠A=30°,
则∠B=60°,所以△CBD为等边三角形,
于是得:BC=CD=BD=AB.
新课探究
结论
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
直角三角形性质定理:
C
B
A
30°
图形语言:
已知△ABC中, ∠ACB=90°,
∠B=30°(∠A=60°),
那么:AC= AB
03
新知探究
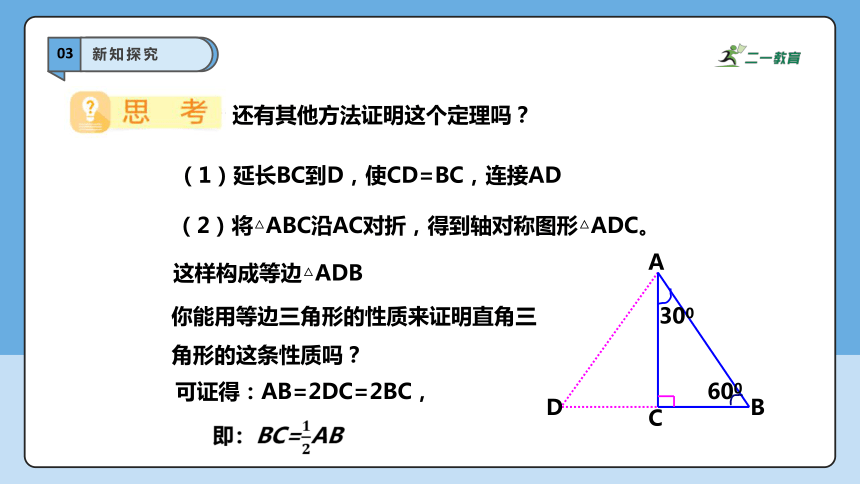
还有其他方法证明这个定理吗?
D
A
C
B
300
600
你能用等边三角形的性质来证明直角三角形的这条性质吗?
(1)延长BC到D,使CD=BC,连接AD
(2)将△ABC沿AC对折,得到轴对称图形△ADC。
这样构成等边△ADB
可证得:AB=2DC=2BC,
即:BC=AB
03
新知探究
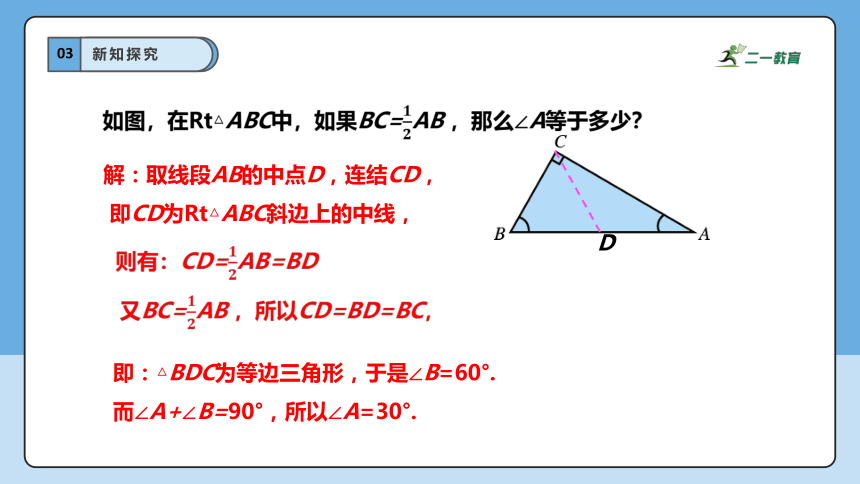
解:取线段AB的中点D,连结CD,
即CD为Rt△ABC斜边上的中线,
D
如图,在Rt△ABC中,如果BC=AB ,那么∠A等于多少?
则有:CD=AB=BD
又BC=AB ,所以CD=BD=BC,
即:△BDC为等边三角形,于是∠B=60°.
而∠A+∠B=90°,所以∠A=30°.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
逆定理
结论
03
新知讲解
例1
在A岛周围20海里(1海里=1852m)水域内有暗 礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°的方向,且与轮船相距海里,如图.该船如果保持航向不变,有触暗礁的危险吗?
03
新知讲解
分析:轮船在航行过程中,如果与A岛的距离始终大于20海里,则轮船就不会触暗礁.
解:过A点作AD⊥OB,垂足为D.
在Rt△AOD中,AO=30海里,∠AOD=30°.
所以轮船不会触礁.
于是:AD= AO=×30≈25.98(海里)>20海里
04
课堂练习
【知识技能类作业】必做题:
1.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2 cm,则AB的长度是( )
A.2 cm B.4 cm C.8 cm D.16 cm
2.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD 是∠B的平分线,AC=18,则BD的值为 ( )
A、4.9 B、9 C、12 D、15
C
C
04
课堂练习
【知识技能类作业】选做题:
3.如图是某超市一层到二层滚梯示意图.其中 AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为 米.
6
04
课堂练习
【综合拓展类作业】
4、如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:AD=BE;
(2)求AD的长.
04
课堂练习
【综合拓展类作业】
(1)证明:∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=AC.
又∵AE=CD,
∴△ABE≌△CAD(SAS).
∴∠ABE=∠CAD,BE=AD
(2)∵∠BPQ=∠BAP+∠ABE
=∠BAP+∠PAE=∠BAC=60°,
又∵BQ⊥PQ,
∴∠PBQ=30°.
∴PB=2PQ=6.
∴BE=PB+PE=7.
∴AD=BE=7.2
05
课堂小结
直角三角形的性质与判定
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
逆定理:
直角三角形的性质定理:
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
06
作业布置
【知识技能类作业】必做题:
1、如图所示,一个人从山下A点沿30°的坡路登上山顶,他走了500米后到达山顶的点B,则这座山的高度是 米
250
06
作业布置
【知识技能类作业】选做题:
2.如图,在△ABC中,若∠BAC=120°,A B=AC,AD⊥AC于点A,BD=3,则BC=______.
9
06
作业布置
【综合拓展类作业】
3.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
06
作业布置
【综合拓展类作业】
解:(1)∵△ABC是等边三角形
∴∠B=60°.
∵DE∥AB,
∴∠EDC=∠B=60°.
∵EF⊥DE,
∴∠DEF=90°.
∴∠F=90°-∠EDC=30°
(2)∵∠ACB=60°,∠EDC=60°
∴△EDC是等边三角形.
∴ED=DC=2.
又∵∠DEF=90°,∠F=30°,
∴DF=2DE=4.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
1.1.2直角三角形的性质和判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
掌握直角掌握直角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半”三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜掌握直角三角形的性掌握直角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直掌握直角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它
掌握直角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半”角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半”果一个锐角等于30度,那么它所对的直角边等于斜边的一半”边的一半”
01
02
03
体会从“一般到特殊”的思维方法和“逆向思维”方法,培养逆向思维能力.
掌握直角三角形的性质“直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30度”.
02
新知导入
思考:一个三角形应满足什么条件才能是直角三角形
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和是90°的三角形是直角三角形;
(3)一边上的中线等于这条边的一半的三角形是直角三角形。
在Rt △ABC中,∠BCA=90°,如果∠A=30°,那么BC与斜边AB有什么关系呢?
分析:1.辅助线的常用作法有 :
30 °
B
C
A
作平行线、中线、垂线、角平分线、延长线,作相等的角等等。
2、你打算怎样作辅助线?
03
新知探究
D
证明:取线段AB的中点D,连结CD,
即CD为Rt△ABC斜边AB上的中线.
则有:CD=AB=BD
因为∠A+∠B=90°, 且∠A=30°,
则∠B=60°,所以△CBD为等边三角形,
于是得:BC=CD=BD=AB.
新课探究
结论
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
直角三角形性质定理:
C
B
A
30°
图形语言:
已知△ABC中, ∠ACB=90°,
∠B=30°(∠A=60°),
那么:AC= AB
03
新知探究
还有其他方法证明这个定理吗?
D
A
C
B
300
600
你能用等边三角形的性质来证明直角三角形的这条性质吗?
(1)延长BC到D,使CD=BC,连接AD
(2)将△ABC沿AC对折,得到轴对称图形△ADC。
这样构成等边△ADB
可证得:AB=2DC=2BC,
即:BC=AB
03
新知探究
解:取线段AB的中点D,连结CD,
即CD为Rt△ABC斜边上的中线,
D
如图,在Rt△ABC中,如果BC=AB ,那么∠A等于多少?
则有:CD=AB=BD
又BC=AB ,所以CD=BD=BC,
即:△BDC为等边三角形,于是∠B=60°.
而∠A+∠B=90°,所以∠A=30°.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
逆定理
结论
03
新知讲解
例1
在A岛周围20海里(1海里=1852m)水域内有暗 礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°的方向,且与轮船相距海里,如图.该船如果保持航向不变,有触暗礁的危险吗?
03
新知讲解
分析:轮船在航行过程中,如果与A岛的距离始终大于20海里,则轮船就不会触暗礁.
解:过A点作AD⊥OB,垂足为D.
在Rt△AOD中,AO=30海里,∠AOD=30°.
所以轮船不会触礁.
于是:AD= AO=×30≈25.98(海里)>20海里
04
课堂练习
【知识技能类作业】必做题:
1.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2 cm,则AB的长度是( )
A.2 cm B.4 cm C.8 cm D.16 cm
2.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD 是∠B的平分线,AC=18,则BD的值为 ( )
A、4.9 B、9 C、12 D、15
C
C
04
课堂练习
【知识技能类作业】选做题:
3.如图是某超市一层到二层滚梯示意图.其中 AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为 米.
6
04
课堂练习
【综合拓展类作业】
4、如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:AD=BE;
(2)求AD的长.
04
课堂练习
【综合拓展类作业】
(1)证明:∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=AC.
又∵AE=CD,
∴△ABE≌△CAD(SAS).
∴∠ABE=∠CAD,BE=AD
(2)∵∠BPQ=∠BAP+∠ABE
=∠BAP+∠PAE=∠BAC=60°,
又∵BQ⊥PQ,
∴∠PBQ=30°.
∴PB=2PQ=6.
∴BE=PB+PE=7.
∴AD=BE=7.2
05
课堂小结
直角三角形的性质与判定
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
逆定理:
直角三角形的性质定理:
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
06
作业布置
【知识技能类作业】必做题:
1、如图所示,一个人从山下A点沿30°的坡路登上山顶,他走了500米后到达山顶的点B,则这座山的高度是 米
250
06
作业布置
【知识技能类作业】选做题:
2.如图,在△ABC中,若∠BAC=120°,A B=AC,AD⊥AC于点A,BD=3,则BC=______.
9
06
作业布置
【综合拓展类作业】
3.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
06
作业布置
【综合拓展类作业】
解:(1)∵△ABC是等边三角形
∴∠B=60°.
∵DE∥AB,
∴∠EDC=∠B=60°.
∵EF⊥DE,
∴∠DEF=90°.
∴∠F=90°-∠EDC=30°
(2)∵∠ACB=60°,∠EDC=60°
∴△EDC是等边三角形.
∴ED=DC=2.
又∵∠DEF=90°,∠F=30°,
∴DF=2DE=4.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
