1.1.2直角三角形的性质和判定 学案
文档属性
| 名称 | 1.1.2直角三角形的性质和判定 学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 297.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
学习任务单
课程基本信息
学科 数学 年级 九年级 学期 秋季
课题 1.1.2直角三角形的性质与判定
教科书 书 名:义务教育教科书数学八年级下册 出版社:湖南教育出版社
学生信息
姓名 学校 班级 学号
学习目标
1.掌握直角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半” . 2.掌握直角三角形的性质“直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30度”.
课前学习任务
复习引入 复习引入 1、直角三角形有哪些性质?结合图形,用图形语言叙述。 Rt ABC中,∠C=90°,D是AB的中点 ∠A+ ∠B=90° CD=AD=BD=AB 2、一个三角形应满足什么条件才能是直角三角形 (1)有一个角是直角的三角形是直角三角形; (2)有两个角的和是90°的三角形是直角三角形; (3)一边上的中线等于这条边的一半的三角形是直角三角形。
课上学习任务
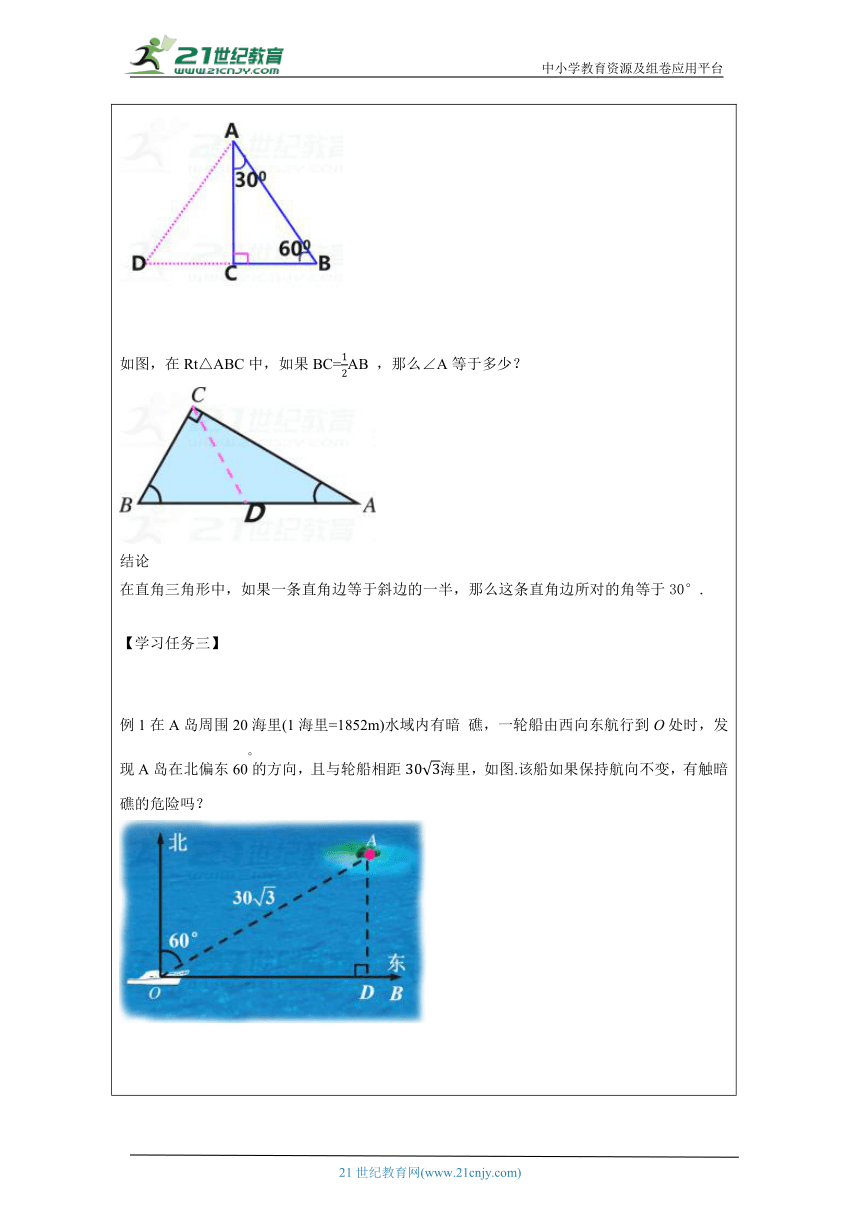
【学习任务一】 在Rt △ABC中,∠BCA=90°,如果∠A=30°,那么BC与斜边AB有什么关系呢? 分析:1.辅助线的常用作法有 : 作平行线、中线、垂线、角平分线、延长线,作相等的角等等。 2、你打算怎样作辅助线? 结论:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半. 图形语言: 已知△ABC中, ∠ACB=90°,∠B=30°(∠A=60°), 那么:AC= AB 【学习任务二】 探究 想一想:还有其他方法证明这个定理吗? 延长BC到D,使CD=BC,连接AD 将△ABC沿AC对折,得到轴对称图形△ADC。 这样构成等边△ADB 你能用等边三角形的性质来证明直角三角形的这条性质吗? 可证得:AB=2DC=2BC, 即:BC=AB 如图,在Rt△ABC中,如果BC=AB ,那么∠A等于多少? 结论 在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°. 【学习任务三】 例1在A岛周围20海里(1海里=1852m)水域内有暗 礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°的方向,且与轮船相距海里,如图.该船如果保持航向不变,有触暗礁的危险吗? 【学习任务四】课堂练习 必做题: 1.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2 cm,则AB的长度是( ) A.2 cm B.4 cm C.8 cm D.16 cm 答案:C 2.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD 是∠B的平分线,AC=18,则BD的值为 ( ) A、4.9 B、9 C、12 D、15 选做题: 3.如图是某超市一层到二层滚梯示意图.其中 AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为 米. 【综合拓展类作业】 4、如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1. (1)求证:AD=BE; (2)求AD的长. 【知识技能类作业】 必做题: 1、如图所示,一个人从山下A点沿30°的坡路登上山顶,他走了500米后到达山顶的点B,则这座山的高度是 米 选做题: 2.如图,在△ABC中,若∠BAC=120°,A B=AC,AD⊥AC于点A,BD=3,则BC=______. 【综合拓展类作业】 3.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F. (1)求∠F的度数; (2)若CD=2,求DF的长.
21世纪教育网(www.21cnjy.com)
学习任务单
课程基本信息
学科 数学 年级 九年级 学期 秋季
课题 1.1.2直角三角形的性质与判定
教科书 书 名:义务教育教科书数学八年级下册 出版社:湖南教育出版社
学生信息
姓名 学校 班级 学号
学习目标
1.掌握直角三角形的性质“直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半” . 2.掌握直角三角形的性质“直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30度”.
课前学习任务
复习引入 复习引入 1、直角三角形有哪些性质?结合图形,用图形语言叙述。 Rt ABC中,∠C=90°,D是AB的中点 ∠A+ ∠B=90° CD=AD=BD=AB 2、一个三角形应满足什么条件才能是直角三角形 (1)有一个角是直角的三角形是直角三角形; (2)有两个角的和是90°的三角形是直角三角形; (3)一边上的中线等于这条边的一半的三角形是直角三角形。
课上学习任务
【学习任务一】 在Rt △ABC中,∠BCA=90°,如果∠A=30°,那么BC与斜边AB有什么关系呢? 分析:1.辅助线的常用作法有 : 作平行线、中线、垂线、角平分线、延长线,作相等的角等等。 2、你打算怎样作辅助线? 结论:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半. 图形语言: 已知△ABC中, ∠ACB=90°,∠B=30°(∠A=60°), 那么:AC= AB 【学习任务二】 探究 想一想:还有其他方法证明这个定理吗? 延长BC到D,使CD=BC,连接AD 将△ABC沿AC对折,得到轴对称图形△ADC。 这样构成等边△ADB 你能用等边三角形的性质来证明直角三角形的这条性质吗? 可证得:AB=2DC=2BC, 即:BC=AB 如图,在Rt△ABC中,如果BC=AB ,那么∠A等于多少? 结论 在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°. 【学习任务三】 例1在A岛周围20海里(1海里=1852m)水域内有暗 礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°的方向,且与轮船相距海里,如图.该船如果保持航向不变,有触暗礁的危险吗? 【学习任务四】课堂练习 必做题: 1.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2 cm,则AB的长度是( ) A.2 cm B.4 cm C.8 cm D.16 cm 答案:C 2.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD 是∠B的平分线,AC=18,则BD的值为 ( ) A、4.9 B、9 C、12 D、15 选做题: 3.如图是某超市一层到二层滚梯示意图.其中 AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为 米. 【综合拓展类作业】 4、如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1. (1)求证:AD=BE; (2)求AD的长. 【知识技能类作业】 必做题: 1、如图所示,一个人从山下A点沿30°的坡路登上山顶,他走了500米后到达山顶的点B,则这座山的高度是 米 选做题: 2.如图,在△ABC中,若∠BAC=120°,A B=AC,AD⊥AC于点A,BD=3,则BC=______. 【综合拓展类作业】 3.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F. (1)求∠F的度数; (2)若CD=2,求DF的长.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
