浙教版2024年九年级上数学期末模拟卷1(含答案)
文档属性
| 名称 | 浙教版2024年九年级上数学期末模拟卷1(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-28 22:42:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版2024年九年级(上)期末模拟卷(1)(含答案)
数学
一、选择题(本题有10小题,每小题3分,共30分)
1.二次函数图象的顶点坐标是( )
A.(-1,-2) B.(1,-2) C.(-1,2) D.(1,2)
2.下列各组中的四条线段成比列的是( )
A. 1cm、2cm、20cm、30cm B. 1cm、2cm、3cm、4cm
C. 4cm、2cm、1cm、3cm D. 5cm、10cm、10cm、20cm
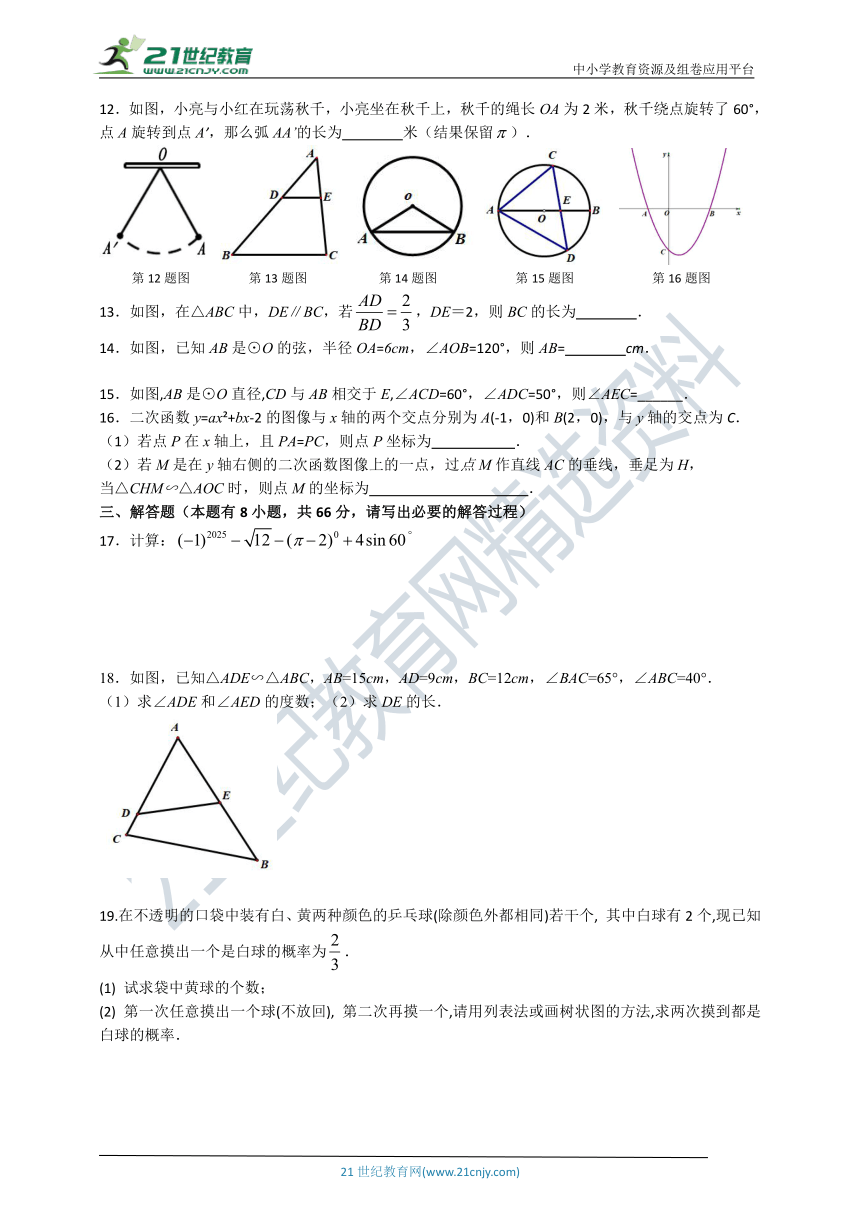
3.如图,点A、B、C在⊙O上,若,则的度数为( )
A.20° B.30° C.40° D.70°
第3题图 第6题图 第7题图 第10题图
4.若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
A. 1:2 B. 1:4 C. 1:5 D. 1:16
5.在Rt△ABC中,∠C=90°,AC=8,BC=6,则△ABC外接圆的半径为( )
A. 10 B. 5 C. 6 D. 4
6.如图,AB与⊙O相切于点B,AO=6cm,AB=4cm.则⊙O的半径为( )
A.cm B.cm C.cm D.cm
7.如图,河堤横断面迎水坡AB的坡比是,堤高BC=5m,则坡面AB的长度是( )
A.10m B.m C.m D.m
8.抛物线y=-x2经过平移得到,平移方法是( )
A.先向右平移1个单位,再向下平移2个单位 B.先向右平移1个单位,再向上平移2个单位
C.先向左平移1个单位,再向下平移2个单位 D.先向左平移1个单位,再向上平移2个单位
9.下列图中的每个矩形都是由五个相同的小正方形拼合组成,其中ΔABC和ΔCDE的顶点都在小正方形的顶点上,则ΔABC与ΔCDE一定相似的图形是( )
A. B.
C. D.
10.如图,一张半径为1的圆形纸片在边长为(≥4)的正三角形内任意移动.则在该正三角形内,这张圆形纸片“不能接触到的部分”的面积是( )
A. B. C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.若,则=________.
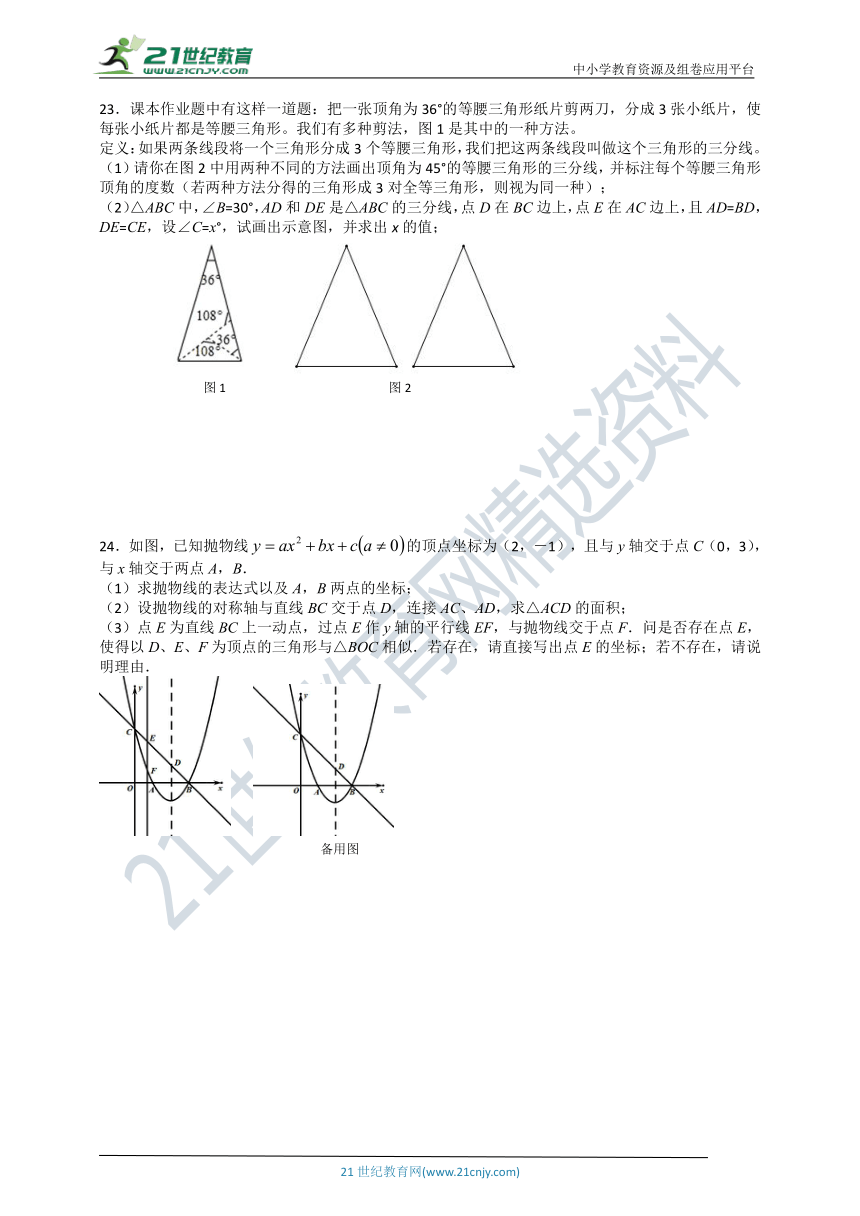
12.如图,小亮与小红在玩荡秋千,小亮坐在秋千上,秋千的绳长OA为2米,秋千绕点旋转了60°,点A旋转到点A’,那么弧AA’的长为 米(结果保留).
第12题图 第13题图 第14题图 第15题图 第16题图
13.如图,在△ABC中,DE∥BC,若,DE=2,则BC的长为 .
14.如图,已知AB是⊙O的弦,半径OA=6cm,∠AOB=120°,则AB= cm.
15.如图,AB是⊙O直径,CD与AB相交于E,∠ACD=60°,∠ADC=50°,则∠AEC=______.
16.二次函数y=ax +bx-2的图像与x轴的两个交点分别为A(-1,0)和B(2,0),与y轴的交点为C.
(1)若点P在x轴上,且PA=PC,则点P坐标为 .
(2)若M是在y轴右侧的二次函数图像上的一点,过点M作直线AC的垂线,垂足为H,
当△CHM∽△AOC时,则点M的坐标为 .
三、解答题(本题有8小题,共66分,请写出必要的解答过程)
17.计算:
18.如图,已知△ADE∽△ABC,AB=15cm,AD=9cm,BC=12cm,∠BAC=65°,∠ABC=40°.
(1)求∠ADE和∠AED的度数;(2)求DE的长.
19.在不透明的口袋中装有白、黄两种颜色的乒乓球(除颜色外都相同)若干个, 其中白球有2个,现已知从中任意摸出一个是白球的概率为.
(1) 试求袋中黄球的个数;
(2) 第一次任意摸出一个球(不放回), 第二次再摸一个,请用列表法或画树状图的方法,求两次摸到都是白球的概率.
20.如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG30,在E处测得∠AFG60,CE8米,仪器高度CD1.5米,求这棵树AB的高度(结果精确到0.1米,≈1.73).
(
A
G
B
F
E
C
D
30
60
)
某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
当每个房间每天的定价为280元的时候,求宾馆客房部每天的利润;
(2)设每个房间每天的定价增加x元,宾馆客房部每天的利润为w元,当每个房间的定价为每天多少元时,每天的利润有最大值?最大值是多少?
22.如图,点A为⊙O 直径CB延长线上一点,过点A作⊙O的切线AD, 切点为D,过点D作DE⊥AC,垂足为,连结BE、CD、CE,已知∠BED=30°.
(1)求sinA的值.
(2)若AB=2,试求⊙O的半径长.
(3)在(2)的条件下,求图中阴影部分的面积.
23.课本作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形。我们有多种剪法,图1是其中的一种方法。
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线。
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x的值;
图1 图2
24.如图,已知抛物线的顶点坐标为(2,-1),且与y轴交于点C(0,3),与x轴交于两点A,B.
(1)求抛物线的表达式以及A,B两点的坐标;
(2)设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BOC相似.若存在,请直接写出点E的坐标;若不存在,请说明理由.
备用图
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1-5 BDCAB 6-10 CDBBA
二.填空题(共6小题,满分18分,每小题4分)
11.2:7 12. 13.5
15.80 16.(1)(1.5,0) (2)(1,-2)或者
三.解答题(共8小题,满分66分)
17.解:原式=-2
18.解:(1)∠ADE=40°,∠AED=75°
(2)DE=5.4
19.解:(1)黄球1个
(2)两次白球概率是;
20.解:(1)根据题意得:四边形DCEF、DCBG是矩形,
则GB=EF=CD=1.5米,DF=CE=8米,
设AG=x米,GF=y米,在Rt△AFG中,tan∠AFG=tan60°,
在Rt△ADG中,tan∠ADG=tan30°,
∴x=4,y=4,∴AG=4米,FG=4米,
∴AB=AG+GB=41.5≈8.4(米).
∴这棵树AB的高度为8.4米.
21.解:(1)由题意得:13520
(2)w=(200+x)(60)﹣20×(60)42x+10800
(x﹣210)2+15210
当x=210时,w有最大值.
此时,x+200=410,就是说,当每个房间的定价为每天410元时,w有最大值,且最大值是15210元.
22.解:解:(1)连接OD,
∵DA为⊙O的切线,切点为D,
∴OD⊥AD,∠ADO=90°,
又∵∠BED=30°,
∴∠BOD=60°,
∴∠A=30°,
∴tanA.
(2)过点O作OG⊥EC于点G
∴,
得R=2,
∴OC=2,
∵DE⊥AC,BC为直径,
∴弧BE=弧BD,
∴∠ECB=∠BED=30°,
∴CE=2CG=2 OCcos30°.
(3)∵由(1)∠BOD=60°得∠ODF=30°,
∴OFODOB,即OF=FB,
由DE⊥AC,BC为直径,
得EF=FD,∠OFD=∠BFE=90°,
∴△BEF≌△ODF,
∴阴影部分面积等于扇形BOD的面积.
23.解:(1)如图2作图,
(2)如图3 ①、②作△ABC.
①当AD=AE时,
∵2x+x=30+30,
∴x=20.
②当AD=DE时,
∵30+30+2x+x=180,
∴x=40.
所以∠C的度数是20°或40°.
24.解:(1)∵抛物线的顶点为(2,﹣1),
∴可设该函数解析式为:y=a(x﹣2)2﹣1(a≠0),
又∵抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),
∴3=a(0﹣2)2﹣1,
解得a=1,
∴该抛物线的解析式是y=(x﹣2)2﹣1(或y=x2﹣4x+3);
(2)在y=x2﹣4x+3中,令y=0,则x2﹣4x+3=0,解得:x1=1,x2=3,
∴A(1,0),B(3,0),
∴直线BC的解析式为y=﹣x+3,
∵抛物线y=(x﹣2)2﹣1的对称轴x=2,D点是抛物线的对称轴与直线BC的交点,
∴当x=2时,y=1,
∴D(2,1),
∴S△ACD=S△ABC﹣S△ABD2;
假设存在点E,使得以D、E、F为顶点的三角形与△BCO相似.
由(1)知,该抛物线的解析式是y=x2﹣4x+3,即y=(x﹣1)(x﹣3),
∴该抛物线与x轴的交点坐标分别是A(1,0),B(3,0).
∵C(0,3),
∴易求直线BC的解析式为:y=﹣x+3.
∴∠OBC=∠OCB=45°.
又∵点D是对称轴上的一点,
∴D(2,1).
如图,连接DF.
∵EF∥y轴,
∴只有∠EFD=∠COB=90°.
∵以D、E、F为顶点的三角形与△BCO相似,
∴∠DEF=∠FDE=45°,
∴只有△EFD∽△COB.
设E(x,﹣x+3),则F(x,1),
∴1=x2﹣4x+3,
解得x=2±,
∠EDF=90°;易知,直线AD:y=x﹣1,联立抛物线的解析式有:
x2﹣4x+3=x﹣1,解得 x1=1、x2=4;
当x=1时,y=﹣x+3=2;
当x=4时,y=﹣x+3=﹣1;
∴E3(1,2)、E4(4,﹣1).
∴E(2,1)或E′(2,1)或(1,2)或(4,﹣1).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙教版2024年九年级(上)期末模拟卷(1)(含答案)
数学
一、选择题(本题有10小题,每小题3分,共30分)
1.二次函数图象的顶点坐标是( )
A.(-1,-2) B.(1,-2) C.(-1,2) D.(1,2)
2.下列各组中的四条线段成比列的是( )
A. 1cm、2cm、20cm、30cm B. 1cm、2cm、3cm、4cm
C. 4cm、2cm、1cm、3cm D. 5cm、10cm、10cm、20cm
3.如图,点A、B、C在⊙O上,若,则的度数为( )
A.20° B.30° C.40° D.70°
第3题图 第6题图 第7题图 第10题图
4.若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
A. 1:2 B. 1:4 C. 1:5 D. 1:16
5.在Rt△ABC中,∠C=90°,AC=8,BC=6,则△ABC外接圆的半径为( )
A. 10 B. 5 C. 6 D. 4
6.如图,AB与⊙O相切于点B,AO=6cm,AB=4cm.则⊙O的半径为( )
A.cm B.cm C.cm D.cm
7.如图,河堤横断面迎水坡AB的坡比是,堤高BC=5m,则坡面AB的长度是( )
A.10m B.m C.m D.m
8.抛物线y=-x2经过平移得到,平移方法是( )
A.先向右平移1个单位,再向下平移2个单位 B.先向右平移1个单位,再向上平移2个单位
C.先向左平移1个单位,再向下平移2个单位 D.先向左平移1个单位,再向上平移2个单位
9.下列图中的每个矩形都是由五个相同的小正方形拼合组成,其中ΔABC和ΔCDE的顶点都在小正方形的顶点上,则ΔABC与ΔCDE一定相似的图形是( )
A. B.
C. D.
10.如图,一张半径为1的圆形纸片在边长为(≥4)的正三角形内任意移动.则在该正三角形内,这张圆形纸片“不能接触到的部分”的面积是( )
A. B. C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.若,则=________.
12.如图,小亮与小红在玩荡秋千,小亮坐在秋千上,秋千的绳长OA为2米,秋千绕点旋转了60°,点A旋转到点A’,那么弧AA’的长为 米(结果保留).
第12题图 第13题图 第14题图 第15题图 第16题图
13.如图,在△ABC中,DE∥BC,若,DE=2,则BC的长为 .
14.如图,已知AB是⊙O的弦,半径OA=6cm,∠AOB=120°,则AB= cm.
15.如图,AB是⊙O直径,CD与AB相交于E,∠ACD=60°,∠ADC=50°,则∠AEC=______.
16.二次函数y=ax +bx-2的图像与x轴的两个交点分别为A(-1,0)和B(2,0),与y轴的交点为C.
(1)若点P在x轴上,且PA=PC,则点P坐标为 .
(2)若M是在y轴右侧的二次函数图像上的一点,过点M作直线AC的垂线,垂足为H,
当△CHM∽△AOC时,则点M的坐标为 .
三、解答题(本题有8小题,共66分,请写出必要的解答过程)
17.计算:
18.如图,已知△ADE∽△ABC,AB=15cm,AD=9cm,BC=12cm,∠BAC=65°,∠ABC=40°.
(1)求∠ADE和∠AED的度数;(2)求DE的长.
19.在不透明的口袋中装有白、黄两种颜色的乒乓球(除颜色外都相同)若干个, 其中白球有2个,现已知从中任意摸出一个是白球的概率为.
(1) 试求袋中黄球的个数;
(2) 第一次任意摸出一个球(不放回), 第二次再摸一个,请用列表法或画树状图的方法,求两次摸到都是白球的概率.
20.如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG30,在E处测得∠AFG60,CE8米,仪器高度CD1.5米,求这棵树AB的高度(结果精确到0.1米,≈1.73).
(
A
G
B
F
E
C
D
30
60
)
某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
当每个房间每天的定价为280元的时候,求宾馆客房部每天的利润;
(2)设每个房间每天的定价增加x元,宾馆客房部每天的利润为w元,当每个房间的定价为每天多少元时,每天的利润有最大值?最大值是多少?
22.如图,点A为⊙O 直径CB延长线上一点,过点A作⊙O的切线AD, 切点为D,过点D作DE⊥AC,垂足为,连结BE、CD、CE,已知∠BED=30°.
(1)求sinA的值.
(2)若AB=2,试求⊙O的半径长.
(3)在(2)的条件下,求图中阴影部分的面积.
23.课本作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形。我们有多种剪法,图1是其中的一种方法。
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线。
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x的值;
图1 图2
24.如图,已知抛物线的顶点坐标为(2,-1),且与y轴交于点C(0,3),与x轴交于两点A,B.
(1)求抛物线的表达式以及A,B两点的坐标;
(2)设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BOC相似.若存在,请直接写出点E的坐标;若不存在,请说明理由.
备用图
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1-5 BDCAB 6-10 CDBBA
二.填空题(共6小题,满分18分,每小题4分)
11.2:7 12. 13.5
15.80 16.(1)(1.5,0) (2)(1,-2)或者
三.解答题(共8小题,满分66分)
17.解:原式=-2
18.解:(1)∠ADE=40°,∠AED=75°
(2)DE=5.4
19.解:(1)黄球1个
(2)两次白球概率是;
20.解:(1)根据题意得:四边形DCEF、DCBG是矩形,
则GB=EF=CD=1.5米,DF=CE=8米,
设AG=x米,GF=y米,在Rt△AFG中,tan∠AFG=tan60°,
在Rt△ADG中,tan∠ADG=tan30°,
∴x=4,y=4,∴AG=4米,FG=4米,
∴AB=AG+GB=41.5≈8.4(米).
∴这棵树AB的高度为8.4米.
21.解:(1)由题意得:13520
(2)w=(200+x)(60)﹣20×(60)42x+10800
(x﹣210)2+15210
当x=210时,w有最大值.
此时,x+200=410,就是说,当每个房间的定价为每天410元时,w有最大值,且最大值是15210元.
22.解:解:(1)连接OD,
∵DA为⊙O的切线,切点为D,
∴OD⊥AD,∠ADO=90°,
又∵∠BED=30°,
∴∠BOD=60°,
∴∠A=30°,
∴tanA.
(2)过点O作OG⊥EC于点G
∴,
得R=2,
∴OC=2,
∵DE⊥AC,BC为直径,
∴弧BE=弧BD,
∴∠ECB=∠BED=30°,
∴CE=2CG=2 OCcos30°.
(3)∵由(1)∠BOD=60°得∠ODF=30°,
∴OFODOB,即OF=FB,
由DE⊥AC,BC为直径,
得EF=FD,∠OFD=∠BFE=90°,
∴△BEF≌△ODF,
∴阴影部分面积等于扇形BOD的面积.
23.解:(1)如图2作图,
(2)如图3 ①、②作△ABC.
①当AD=AE时,
∵2x+x=30+30,
∴x=20.
②当AD=DE时,
∵30+30+2x+x=180,
∴x=40.
所以∠C的度数是20°或40°.
24.解:(1)∵抛物线的顶点为(2,﹣1),
∴可设该函数解析式为:y=a(x﹣2)2﹣1(a≠0),
又∵抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),
∴3=a(0﹣2)2﹣1,
解得a=1,
∴该抛物线的解析式是y=(x﹣2)2﹣1(或y=x2﹣4x+3);
(2)在y=x2﹣4x+3中,令y=0,则x2﹣4x+3=0,解得:x1=1,x2=3,
∴A(1,0),B(3,0),
∴直线BC的解析式为y=﹣x+3,
∵抛物线y=(x﹣2)2﹣1的对称轴x=2,D点是抛物线的对称轴与直线BC的交点,
∴当x=2时,y=1,
∴D(2,1),
∴S△ACD=S△ABC﹣S△ABD2;
假设存在点E,使得以D、E、F为顶点的三角形与△BCO相似.
由(1)知,该抛物线的解析式是y=x2﹣4x+3,即y=(x﹣1)(x﹣3),
∴该抛物线与x轴的交点坐标分别是A(1,0),B(3,0).
∵C(0,3),
∴易求直线BC的解析式为:y=﹣x+3.
∴∠OBC=∠OCB=45°.
又∵点D是对称轴上的一点,
∴D(2,1).
如图,连接DF.
∵EF∥y轴,
∴只有∠EFD=∠COB=90°.
∵以D、E、F为顶点的三角形与△BCO相似,
∴∠DEF=∠FDE=45°,
∴只有△EFD∽△COB.
设E(x,﹣x+3),则F(x,1),
∴1=x2﹣4x+3,
解得x=2±,
∠EDF=90°;易知,直线AD:y=x﹣1,联立抛物线的解析式有:
x2﹣4x+3=x﹣1,解得 x1=1、x2=4;
当x=1时,y=﹣x+3=2;
当x=4时,y=﹣x+3=﹣1;
∴E3(1,2)、E4(4,﹣1).
∴E(2,1)或E′(2,1)或(1,2)或(4,﹣1).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
