2025年中考数学二轮专题复习第一章几何最值专题讲练 第5节 瓜豆原理(含解析)
文档属性
| 名称 | 2025年中考数学二轮专题复习第一章几何最值专题讲练 第5节 瓜豆原理(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 340.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览




文档简介
第5节 瓜豆原理
前言:“瓜豆原理”是近来中考最值中的热点话题之一,“瓜豆”是寓意,由一个动点轨迹探究另一动点轨迹,正所谓:种瓜得瓜,种豆得豆. 用数学语言解释即旋转、放缩,本节介绍模型及解题思路.
中小学教育资源及组卷应用平台
知识导航
1 轨迹圆
探究1:如图,P是圆O上一个动点,A为定点,连接AP,Q为AP中点. 当点P在圆O上运动时,探究Q点轨迹.
分析:线段AQ可以理解为由AP放缩得来,
则 P 点轨迹放缩即可得Q 点轨迹,
连接AO, 取AO中点 M,
则M点即为Q 点轨迹圆圆心,半径
任意时刻, 均有△AMQ∽△AOP,
探究2:如图,P是圆O上一个动点,A为定点,连接AP,作AQ⊥AP且AQ=AP. 当点 P在圆O上运动时, 探究Q点轨迹.
分析:AQ可以理解为由AP绕点A逆时针旋转90°得来,则P点轨迹绕点A 逆时针旋转90°即可得Q 点轨迹,∴点Q轨迹也是圆.
点Q轨迹圆圆心M满足AM=AO且AM⊥AO,在任意时刻均有△APO≌△AQM.
探究3:如图,△APQ是直角三角形,∠PAQ=90°且AP=2AQ,当P在圆O运动时,探究Q 点轨迹.
分析: 由AP⊥AQ, 可得Q点轨迹圆圆心M满足AM⊥AO;由 Q点轨迹圆圆心M满足
即可确定圆M位置,
任意时刻均有△APO∽△AQM, 且相似比为2: 1.
模型总结
由 P 点轨迹推Q点轨迹.
通常称点P为“主动点”,点Q为“从动点”.
瓜豆问题的必要条件:两个定量
(1)主动点、从动点与定点连线的夹角是定量(∠PAQ是定值);
(2)主动点、从动点到定点的距离之比是定量(AP:AQ是定值).
模型结论:
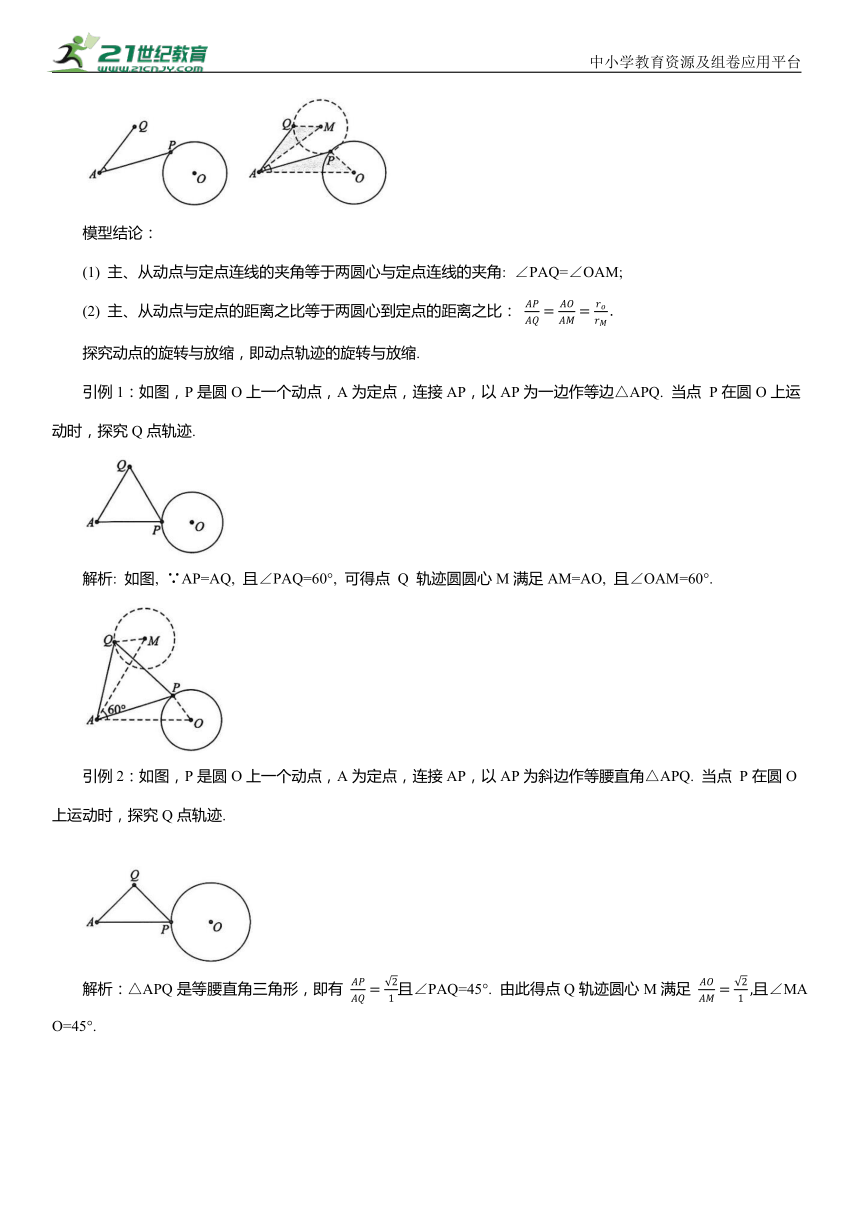
(1) 主、从动点与定点连线的夹角等于两圆心与定点连线的夹角: ∠PAQ=∠OAM;
(2) 主、从动点与定点的距离之比等于两圆心到定点的距离之比:
探究动点的旋转与放缩,即动点轨迹的旋转与放缩.
引例1:如图,P是圆O上一个动点,A为定点,连接AP,以AP为一边作等边△APQ. 当点 P在圆O上运动时,探究Q点轨迹.
解析: 如图, ∵AP=AQ, 且∠PAQ=60°, 可得点 Q 轨迹圆圆心M满足AM=AO, 且∠OAM=60°.
引例2:如图,P是圆O上一个动点,A为定点,连接AP,以AP为斜边作等腰直角△APQ. 当点 P在圆O上运动时,探究Q点轨迹.
解析:△APQ是等腰直角三角形,即有 且∠PAQ=45°. 由此得点Q轨迹圆心M满足 且∠MAO=45°.
2 轨迹直线
探究4: 如图, P 是线段 BC上一动点, 连接AP, 取AP中点Q,当点 P在BC上运动时,探究Q点轨迹.
分析:当P 点轨迹是线段时,Q点轨迹也是一条线段.
分别过A、Q向BC作垂线,垂足分别为M、N,
在运动过程中,
∴Q点到BC的距离是定值,∴Q点轨迹是一条线段,即下图中的线段EF.
探究 5: 如图, △APQ 是等腰直角三角形, ∠PAQ=90°且AP=AQ, 当点 P在线段BC上运动时, 探究Q 点轨迹.
分析:当 AP 与AQ 夹角固定且AP:AQ为定值的话,所以Q 点轨迹也是线段. 分别确定 P 在起点和终点时,点Q 的位置,即可得Q点轨迹.
模型总结
必要条件:两个定量
(1)主动点、从动点与定点连线的夹角是定量(∠PAQ是定值);
(2)主动点、从动点到定点的距离之比是定量(AP:AQ是定值).
模型结论:
(1) P、Q 两点轨迹所在直线的夹角等于∠PAQ.
(当∠PAQ≤90°时, ∠PAQ等于 MN与BC夹角)
(2) P、Q两点轨迹长度之比等于 AP: AQ
(由△ABC∽△AMN, 可得
所谓“种圆得圆”、“种线得线”,谓之“瓜豆原理”.
引例3: 如图, 在等边△ABC中, AB=10, BD=4, BE=2,点P从点 E 出发沿EA方向运动,连结PD,以PD为边,在PD 的右侧按如图所示的方式作等边△DPF,当点 P 从点 E运动到点A时,点F运动的路径长是 .
解析:根据△DPF是等边三角形,∴可知F点运动路径长与P点相同,P从E点运动到A 点路径长为8,
∴F点运动的路径长是8.
3 其它图形
所谓“瓜豆原理”,就是主动与从动点的轨迹的旋转放缩,只需主、从动点满足①夹角定角; ②比例定值,当主动点轨迹是任意图形时,从动点轨迹必然也是与其相似的图形.
引例4:如图,在反比例函数 的图像上有一个动点 A,连接AO 并延长交图像的另一支于点 B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数 的图像上运动,若tan∠CAB=2,k=( )
A. 2 B. 4 C. 6 D. 8
解析: ∠AOC=90°且AO: OC=1: 2, 显然点 C的轨迹也是一条双曲线,分别作AM、CN垂直x轴,垂足分别为M、N,连接OC, 则△AMO∽△ONC, ∴CN=2OM, ON=2AM,∴ON·CN=4AM·OM , ∴k=4×2=8, 故选 D.
引例5: 如图, A(-1, 1), B(-1, 4), C(-5, 4), 点P是△ABC边上一动点, 连接OP, 以OP 为斜边在 OP 的右上方作等腰直角△OPQ,当点 P 在△ABC 边上运动一周时,点Q的轨迹形成的封闭图形面积为 .
解析:根据△OPQ是等腰直角三角形可得:Q点运动轨迹与P 点轨迹形状相同,根据 可得 P 点轨迹图形与Q 点轨迹图形相似比为 :1, ∴面积比为2: 1,△ABC面积为
∴Q 点轨迹形成的封闭图形面积为3.
真题演练
1.如图,在等腰Rt△ABC中, 点P在以斜边AB为直径的半圆上,M为PC的中点,当半圆从点A 运动至点B时,点M运动的路径长为 .
2. 如图, 正方形ABCD中, O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF, 连接AE、CF. 线段OF长的最小值是 .
3. 如图, 点A、B的坐标分别为A(2,0)、B(0,2), 点C为坐标平面内一点, BC=1, 点 M为线段AC的中点,连接OM,则OM的最大值为( )
4.如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线 与x轴、y轴分别交于点D、E, 则△CDE面积的最小值为 .
5. △ABC中, AB=4, AC=2, 以BC为边, 在△ABC外作正方形 BCDE, BD、CE 交于点 O, 则线段 AO 的最大值为
6. 如图所示, AB=4, AC=2, 以BC为底边向上构造等腰直角△BCD, 连接AD并延长至点P, 使AD=PD, 则PB 的取值范围为 .
7. 如图, 在平面内, 线段AB=6, P为线段AB 上的动点,三角形纸片 CDE 的边 CD 所在的直线与线段AB 垂直相较于点 P,且满足PC=PA,若点 P 沿AB 方向从点A运动到点 B,则点 E运动的路径长为 .
8. 如图,已知点 A 是第一象限内横坐标为 2的一个定点, AC⊥x轴于点 M, 交直线y=-x于点N,若点 P 是线段 ON上的一个动点, ∠APB=30°, BA⊥PA, 则点 P 在线段 ON上运动时,A点不变,B点随之运动. 求当点P从点O运动到点N时,点B运动的路径长是 .
9. 如图, 在平面直角坐标系中, A (-3, 0), 点B是y轴正半轴上一动点,点C、D在x正半轴上,以AB为边在AB的下方作等边△ABP,点B在y轴上运动时,OP的最小值是
10. 如图, 在平面直角坐标系中, Q是直线 上的一个动点,将Q绕点P(1,0)顺时针旋转90°, 得到点Q', 连接OQ', 则OQ'的最小值为( )
B.
11. 如图, 正方形ABCD 的边长为4, E为BC上一点, 且BE=1, F为AB边上的一个动点, 连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .
第5讲 瓜豆原理
π.
解析:考虑C、M、P共线及M是CP中点,可确定 M点轨迹: 取AB中点O, 连接CO取CO中点D, 以D为圆心,DM为半径作圆D分别交AC、BC于 E、F两点, 则弧EF即为M点轨迹. ∴M点路径长为
解析:E是主动点,F是从动点,D是定点,E点满足EO=2,故E点轨迹是以O为圆心,2为半径的圆.考虑 DE⊥DF且DE=DF, 故作 DM⊥DO且DM=DO, F点轨迹是以点M为圆心,2为半径的圆.直接连接OM,与圆M交点即为F点,此时 OF 最小. ∴OF的最小值为
,
解析:连接AB,取AB中点N,M点轨迹是以点N为圆心, 为半径的圆,如图当点O、N、M共线时,OM最大,最大值为 故选 B.
解析: 由题意可知点E坐标为(0, -3),点D坐标为 (4,0), 取OA中点M(1, 0), 则点C轨迹是以点M为圆心, 1为半径的圆, 连接 MC 并延长交 DE于点 H, 当CH⊥DE时,CH最小,此时三角形面积最小,CH的最小值为 三角形 CDE 面积的最小值为 即△CDE面积的最小值为2.
解析:固定 AB,将AC 看成动线段,求得线段 AO 的最大值. 根据AC=2,可得C点轨迹是以点A为圆心,2为半径的圆. 观察△BOC 是等腰直角三角形,锐角顶点 C 的轨迹是以点A为圆心,2为半径的圆,所以O点轨迹也是圆,以AB为斜边构造等腰直角三角形,直角顶点 M即为点O轨迹圆圆心. 连接AM并延长与圆 M交点即为所求的点O,此时AO最大,最大值为
固定AB不变,AC=2,则C点轨迹是以A为圆心,2为半径的圆,以BC为斜边作等腰直角三角形BCD,则D点轨迹是以点 M为圆心、 为半径的圆考虑到AP=2AD,故P 点轨迹是以N为圆心,2 为半径的圆,可得PB的取值范围是
解析: 连接CA, 则 可得点C轨迹长为 ∴点E运动的路径长为(
根据∠PAB=90°, ∠APB=30°可得:AP:AB= :1,故B 点轨迹也是线段,且P 点轨迹路径长与 B 点轨迹路径长之比也为 :1,P点轨迹长ON为2 ,故B 点轨迹长为2
解析:求OP 最小值需先作出P 点轨迹,根据△ABP是等边三角形且B 点在直线上运动,故可知 P 点轨迹也是直线. 取两特殊时刻:(1)当点B与点O重合时,作出P 点位置P ;(2) 当点B在x轴上方且AB与x轴夹角为60°时, 作出 P点位置P .连接P P ,即为P点轨迹.根据∠ABP=60°可知:P P 与y轴夹角为60°, 作OP⊥P P , 所得OP长度即为最小值, 所以
. B.
解析:将Q 点轨迹绕点 P顺时针旋转90°即可得点Q'轨迹: 直线y=2x-5, 与x轴交点坐标为( ). 点O到直线y=2x-5的距离为 ,故OQ'的最小值为 , 选B.
解析:将F 点看成是由点B向点A 运动,由此作出 G 点轨迹:考虑到F点轨迹是线段,故G点轨迹也是线段,取起点和终点即可确定线段位置,初始时刻 G 点在G 位置,最终G点在G 位置(G 不一定在CD边), G G 即为G点运动轨迹. CG最小值即当CG⊥G G 的时候取到,作CH⊥G G 于点H,CH 即为所求的最小值. 根据模型可知:G G 与AB夹角为60°, 故( 过点E作EF⊥CH于点F,则 所以 因此CG的最小值为
前言:“瓜豆原理”是近来中考最值中的热点话题之一,“瓜豆”是寓意,由一个动点轨迹探究另一动点轨迹,正所谓:种瓜得瓜,种豆得豆. 用数学语言解释即旋转、放缩,本节介绍模型及解题思路.
中小学教育资源及组卷应用平台
知识导航
1 轨迹圆
探究1:如图,P是圆O上一个动点,A为定点,连接AP,Q为AP中点. 当点P在圆O上运动时,探究Q点轨迹.
分析:线段AQ可以理解为由AP放缩得来,
则 P 点轨迹放缩即可得Q 点轨迹,
连接AO, 取AO中点 M,
则M点即为Q 点轨迹圆圆心,半径
任意时刻, 均有△AMQ∽△AOP,
探究2:如图,P是圆O上一个动点,A为定点,连接AP,作AQ⊥AP且AQ=AP. 当点 P在圆O上运动时, 探究Q点轨迹.
分析:AQ可以理解为由AP绕点A逆时针旋转90°得来,则P点轨迹绕点A 逆时针旋转90°即可得Q 点轨迹,∴点Q轨迹也是圆.
点Q轨迹圆圆心M满足AM=AO且AM⊥AO,在任意时刻均有△APO≌△AQM.
探究3:如图,△APQ是直角三角形,∠PAQ=90°且AP=2AQ,当P在圆O运动时,探究Q 点轨迹.
分析: 由AP⊥AQ, 可得Q点轨迹圆圆心M满足AM⊥AO;由 Q点轨迹圆圆心M满足
即可确定圆M位置,
任意时刻均有△APO∽△AQM, 且相似比为2: 1.
模型总结
由 P 点轨迹推Q点轨迹.
通常称点P为“主动点”,点Q为“从动点”.
瓜豆问题的必要条件:两个定量
(1)主动点、从动点与定点连线的夹角是定量(∠PAQ是定值);
(2)主动点、从动点到定点的距离之比是定量(AP:AQ是定值).
模型结论:
(1) 主、从动点与定点连线的夹角等于两圆心与定点连线的夹角: ∠PAQ=∠OAM;
(2) 主、从动点与定点的距离之比等于两圆心到定点的距离之比:
探究动点的旋转与放缩,即动点轨迹的旋转与放缩.
引例1:如图,P是圆O上一个动点,A为定点,连接AP,以AP为一边作等边△APQ. 当点 P在圆O上运动时,探究Q点轨迹.
解析: 如图, ∵AP=AQ, 且∠PAQ=60°, 可得点 Q 轨迹圆圆心M满足AM=AO, 且∠OAM=60°.
引例2:如图,P是圆O上一个动点,A为定点,连接AP,以AP为斜边作等腰直角△APQ. 当点 P在圆O上运动时,探究Q点轨迹.
解析:△APQ是等腰直角三角形,即有 且∠PAQ=45°. 由此得点Q轨迹圆心M满足 且∠MAO=45°.
2 轨迹直线
探究4: 如图, P 是线段 BC上一动点, 连接AP, 取AP中点Q,当点 P在BC上运动时,探究Q点轨迹.
分析:当P 点轨迹是线段时,Q点轨迹也是一条线段.
分别过A、Q向BC作垂线,垂足分别为M、N,
在运动过程中,
∴Q点到BC的距离是定值,∴Q点轨迹是一条线段,即下图中的线段EF.
探究 5: 如图, △APQ 是等腰直角三角形, ∠PAQ=90°且AP=AQ, 当点 P在线段BC上运动时, 探究Q 点轨迹.
分析:当 AP 与AQ 夹角固定且AP:AQ为定值的话,所以Q 点轨迹也是线段. 分别确定 P 在起点和终点时,点Q 的位置,即可得Q点轨迹.
模型总结
必要条件:两个定量
(1)主动点、从动点与定点连线的夹角是定量(∠PAQ是定值);
(2)主动点、从动点到定点的距离之比是定量(AP:AQ是定值).
模型结论:
(1) P、Q 两点轨迹所在直线的夹角等于∠PAQ.
(当∠PAQ≤90°时, ∠PAQ等于 MN与BC夹角)
(2) P、Q两点轨迹长度之比等于 AP: AQ
(由△ABC∽△AMN, 可得
所谓“种圆得圆”、“种线得线”,谓之“瓜豆原理”.
引例3: 如图, 在等边△ABC中, AB=10, BD=4, BE=2,点P从点 E 出发沿EA方向运动,连结PD,以PD为边,在PD 的右侧按如图所示的方式作等边△DPF,当点 P 从点 E运动到点A时,点F运动的路径长是 .
解析:根据△DPF是等边三角形,∴可知F点运动路径长与P点相同,P从E点运动到A 点路径长为8,
∴F点运动的路径长是8.
3 其它图形
所谓“瓜豆原理”,就是主动与从动点的轨迹的旋转放缩,只需主、从动点满足①夹角定角; ②比例定值,当主动点轨迹是任意图形时,从动点轨迹必然也是与其相似的图形.
引例4:如图,在反比例函数 的图像上有一个动点 A,连接AO 并延长交图像的另一支于点 B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数 的图像上运动,若tan∠CAB=2,k=( )
A. 2 B. 4 C. 6 D. 8
解析: ∠AOC=90°且AO: OC=1: 2, 显然点 C的轨迹也是一条双曲线,分别作AM、CN垂直x轴,垂足分别为M、N,连接OC, 则△AMO∽△ONC, ∴CN=2OM, ON=2AM,∴ON·CN=4AM·OM , ∴k=4×2=8, 故选 D.
引例5: 如图, A(-1, 1), B(-1, 4), C(-5, 4), 点P是△ABC边上一动点, 连接OP, 以OP 为斜边在 OP 的右上方作等腰直角△OPQ,当点 P 在△ABC 边上运动一周时,点Q的轨迹形成的封闭图形面积为 .
解析:根据△OPQ是等腰直角三角形可得:Q点运动轨迹与P 点轨迹形状相同,根据 可得 P 点轨迹图形与Q 点轨迹图形相似比为 :1, ∴面积比为2: 1,△ABC面积为
∴Q 点轨迹形成的封闭图形面积为3.
真题演练
1.如图,在等腰Rt△ABC中, 点P在以斜边AB为直径的半圆上,M为PC的中点,当半圆从点A 运动至点B时,点M运动的路径长为 .
2. 如图, 正方形ABCD中, O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF, 连接AE、CF. 线段OF长的最小值是 .
3. 如图, 点A、B的坐标分别为A(2,0)、B(0,2), 点C为坐标平面内一点, BC=1, 点 M为线段AC的中点,连接OM,则OM的最大值为( )
4.如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线 与x轴、y轴分别交于点D、E, 则△CDE面积的最小值为 .
5. △ABC中, AB=4, AC=2, 以BC为边, 在△ABC外作正方形 BCDE, BD、CE 交于点 O, 则线段 AO 的最大值为
6. 如图所示, AB=4, AC=2, 以BC为底边向上构造等腰直角△BCD, 连接AD并延长至点P, 使AD=PD, 则PB 的取值范围为 .
7. 如图, 在平面内, 线段AB=6, P为线段AB 上的动点,三角形纸片 CDE 的边 CD 所在的直线与线段AB 垂直相较于点 P,且满足PC=PA,若点 P 沿AB 方向从点A运动到点 B,则点 E运动的路径长为 .
8. 如图,已知点 A 是第一象限内横坐标为 2的一个定点, AC⊥x轴于点 M, 交直线y=-x于点N,若点 P 是线段 ON上的一个动点, ∠APB=30°, BA⊥PA, 则点 P 在线段 ON上运动时,A点不变,B点随之运动. 求当点P从点O运动到点N时,点B运动的路径长是 .
9. 如图, 在平面直角坐标系中, A (-3, 0), 点B是y轴正半轴上一动点,点C、D在x正半轴上,以AB为边在AB的下方作等边△ABP,点B在y轴上运动时,OP的最小值是
10. 如图, 在平面直角坐标系中, Q是直线 上的一个动点,将Q绕点P(1,0)顺时针旋转90°, 得到点Q', 连接OQ', 则OQ'的最小值为( )
B.
11. 如图, 正方形ABCD 的边长为4, E为BC上一点, 且BE=1, F为AB边上的一个动点, 连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .
第5讲 瓜豆原理
π.
解析:考虑C、M、P共线及M是CP中点,可确定 M点轨迹: 取AB中点O, 连接CO取CO中点D, 以D为圆心,DM为半径作圆D分别交AC、BC于 E、F两点, 则弧EF即为M点轨迹. ∴M点路径长为
解析:E是主动点,F是从动点,D是定点,E点满足EO=2,故E点轨迹是以O为圆心,2为半径的圆.考虑 DE⊥DF且DE=DF, 故作 DM⊥DO且DM=DO, F点轨迹是以点M为圆心,2为半径的圆.直接连接OM,与圆M交点即为F点,此时 OF 最小. ∴OF的最小值为
,
解析:连接AB,取AB中点N,M点轨迹是以点N为圆心, 为半径的圆,如图当点O、N、M共线时,OM最大,最大值为 故选 B.
解析: 由题意可知点E坐标为(0, -3),点D坐标为 (4,0), 取OA中点M(1, 0), 则点C轨迹是以点M为圆心, 1为半径的圆, 连接 MC 并延长交 DE于点 H, 当CH⊥DE时,CH最小,此时三角形面积最小,CH的最小值为 三角形 CDE 面积的最小值为 即△CDE面积的最小值为2.
解析:固定 AB,将AC 看成动线段,求得线段 AO 的最大值. 根据AC=2,可得C点轨迹是以点A为圆心,2为半径的圆. 观察△BOC 是等腰直角三角形,锐角顶点 C 的轨迹是以点A为圆心,2为半径的圆,所以O点轨迹也是圆,以AB为斜边构造等腰直角三角形,直角顶点 M即为点O轨迹圆圆心. 连接AM并延长与圆 M交点即为所求的点O,此时AO最大,最大值为
固定AB不变,AC=2,则C点轨迹是以A为圆心,2为半径的圆,以BC为斜边作等腰直角三角形BCD,则D点轨迹是以点 M为圆心、 为半径的圆考虑到AP=2AD,故P 点轨迹是以N为圆心,2 为半径的圆,可得PB的取值范围是
解析: 连接CA, 则 可得点C轨迹长为 ∴点E运动的路径长为(
根据∠PAB=90°, ∠APB=30°可得:AP:AB= :1,故B 点轨迹也是线段,且P 点轨迹路径长与 B 点轨迹路径长之比也为 :1,P点轨迹长ON为2 ,故B 点轨迹长为2
解析:求OP 最小值需先作出P 点轨迹,根据△ABP是等边三角形且B 点在直线上运动,故可知 P 点轨迹也是直线. 取两特殊时刻:(1)当点B与点O重合时,作出P 点位置P ;(2) 当点B在x轴上方且AB与x轴夹角为60°时, 作出 P点位置P .连接P P ,即为P点轨迹.根据∠ABP=60°可知:P P 与y轴夹角为60°, 作OP⊥P P , 所得OP长度即为最小值, 所以
. B.
解析:将Q 点轨迹绕点 P顺时针旋转90°即可得点Q'轨迹: 直线y=2x-5, 与x轴交点坐标为( ). 点O到直线y=2x-5的距离为 ,故OQ'的最小值为 , 选B.
解析:将F 点看成是由点B向点A 运动,由此作出 G 点轨迹:考虑到F点轨迹是线段,故G点轨迹也是线段,取起点和终点即可确定线段位置,初始时刻 G 点在G 位置,最终G点在G 位置(G 不一定在CD边), G G 即为G点运动轨迹. CG最小值即当CG⊥G G 的时候取到,作CH⊥G G 于点H,CH 即为所求的最小值. 根据模型可知:G G 与AB夹角为60°, 故( 过点E作EF⊥CH于点F,则 所以 因此CG的最小值为
同课章节目录
