2025年中考数学二轮专题复习 第2章 对称与旋转压轴题讲练第10节 从全等到相似 (含解析)
文档属性
| 名称 | 2025年中考数学二轮专题复习 第2章 对称与旋转压轴题讲练第10节 从全等到相似 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 511.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 07:09:58 | ||
图片预览




文档简介
第10节 从全等到相似
前言:旋转问题的探究题是近来中考题中的热点题型之一,此类问题一般从旋转的性质出发,探究旋转型全等与相似.
知 识 导 航
从全等到相似
在手拉手模型中,我们可以看成是两个相似的等腰三角形作共点旋转,由等腰条件可得一组全等三角形.
若△ABC与△ADE非等腰,则可得到旋转型相似.
以直角三角形为例:
如图, Rt△ABC∽Rt△ADE, 连接BD、CE.
可得:△ADB∽△AEC,且旋转的性质,旋转角都相等依然成立, 如下右图, ∠BAD=∠EAC=∠EFB.
引例1:如图,在Rt△ABC中,∠ACB=90°, BC=6,AC=8,点 D、E 分别是边AB、BC的中点, 连接DE, 将△BDE绕点 B 按顺时针方向旋转一定角度(小于 90°) 后,点D 的对应点D'和点 E 的对应点E'以及点 A 三个点在一直线上,连接CE', 则CE'= .
解析: ∵BE'=BE=3, AB=10,
又
由题意得: △BE'C∽△BD'A,
引例2:(1) 问题发现
如图1, 在△OAB和△OCD中, OA=OB, OC=OD,∠AOB=∠COD=40°, 连接AC, BD交于点 M. 填空: 的值为 ; ②∠AMB的度数为 .
(2) 类比探究
如图2, 在△OAB和△OCD中, ∠AOB=∠COD=90°,∠OAB=∠OCD=30°, 连接AC交BD的延长线于点 M.请判断 的值及∠AMB的度数,并说明理由;
(3) 拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC、BD所在直线交于点 M,若OD=1, OB= 请直接写出当点C与点 M重合时AC的长.
中小学教育资源及组卷应用平台
解析: (1) 由题意可证△AOC≌△BOD,
∴①∠CBD=1, ②∠AMB=∠AOB=40°.(旋转角都相等)
(2)∵∠AOB=∠COD=90°, ∠OAB=∠OCD=30°,
又∠AOC=90°+∠AOD=∠BOD, ∴△AOC∽△BOD,
∵∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=90°.
的值为 , ∠AMB的度数为90°.
(3) 如下左图, 可证△OCA∽△ODB, 设BD=x,则AC= x, ∵OD=1, ∴CD=2,
勾股定理: 解得: x=2,
如上右图, 由题意得: △OAC∽△OBD, 设BC=x,则 又. 解得: x=1, ∴AC=3 综上所述,AC的长为2 或3
真题演练
1.如图,两个大小不同的三角板放在同一平面内,直角顶点重合于点 C,点D在AB上,
∠BAC=∠DEC=30°, AC与DE交于点 F, 连接AE, 若BD=1, AD=5, 则
2. 如图,正方形ABCD的边长为5 ,点E是正方形ABCD内一点,将△BCE绕着点 C顺时针旋转90°,点E的对应点 F 和点 B、E在一条直线上,BF 与对角线 AC 相较于点G, 若DF=6, 则GF的长为 .
3. 如图, 在 Rt△ABC中, ∠ACB=90°,∠B=60°, D为AB边的中点, 连接DC过D作DE⊥DC交AC于点E.
(1) 求∠EDA的度数;
(2) 如图2, F为BC边上一点, 连接DF, 过D 作 DG⊥DF交AC于点G,请判断线段CF与EG的数量关系,并说明理由.
4.在菱形ABCD中, ∠ABC=60°, 点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点 P的位置变化而变化.
(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是 ,CE与AD的位置关系是 ;
(2) 当点 E在菱形ABCD外部时,(1)中的结论是否还成立 若成立,请予以证明; 若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);
(3) 如图4, 当点 P 在线段 BD 的延长线上时, 连接BE,若 求四边形ADPE的面积.
5.在数学兴趣小组活动中,小亮进行数学探究活动. △ABC是边长为2 的等边三角形,E是AC上一点,小亮以 BE为边向 BE 的右侧作等边三角形 BEF,连接CF.
(1)如图1,当点E在线段AC上时, EF、BC相交于点 D,小亮发现有两个三角形全等,请你找出来,并证明.
(2) 当点 E 在线段AC 上运动时,点F 也随着运动,若四边形ABFC的面积为 求AE的长.
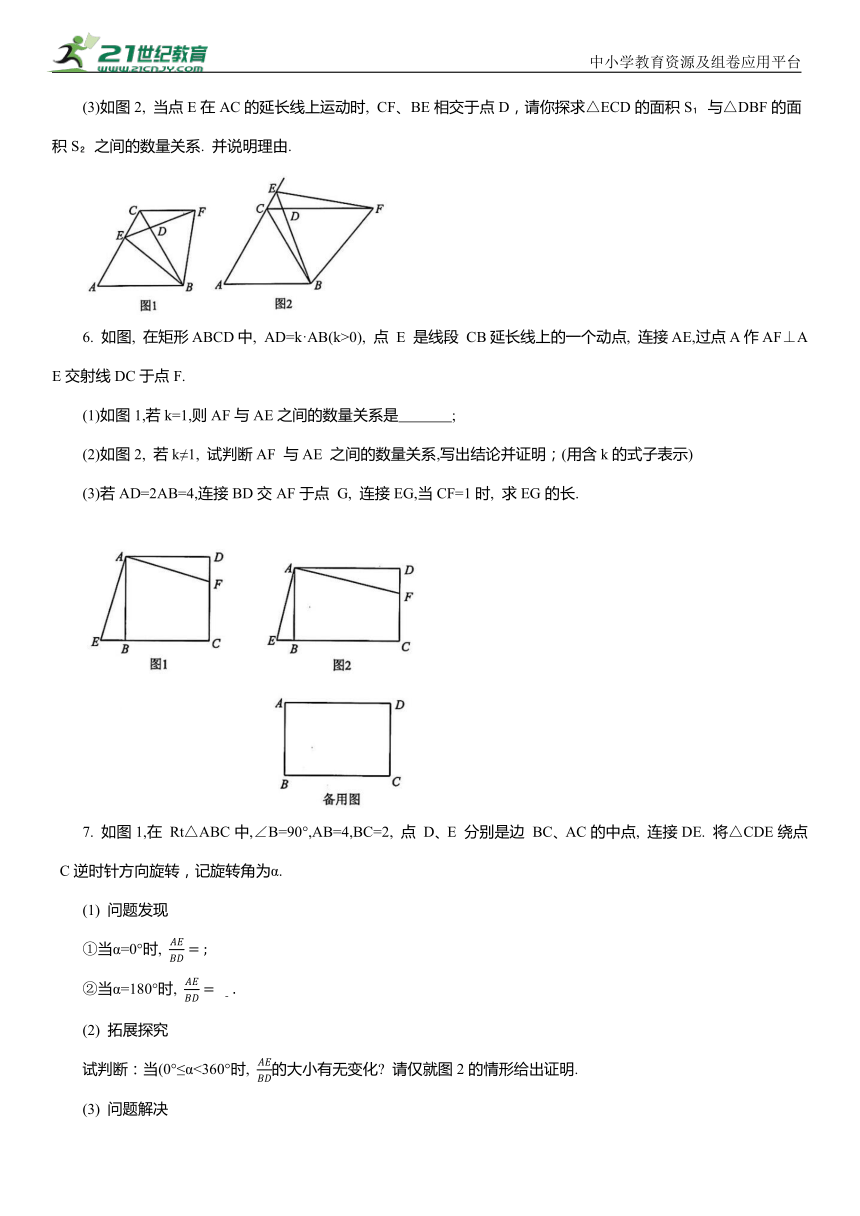
(3)如图2, 当点E在AC的延长线上运动时, CF、BE相交于点D,请你探求△ECD的面积S 与△DBF的面积S 之间的数量关系. 并说明理由.
6. 如图, 在矩形ABCD中, AD=k·AB(k>0), 点 E 是线段 CB延长线上的一个动点, 连接AE,过点A作AF⊥AE交射线DC于点F.
(1)如图1,若k=1,则AF与AE之间的数量关系是 ;
(2)如图2, 若k≠1, 试判断AF 与AE 之间的数量关系,写出结论并证明;(用含k的式子表示)
(3)若AD=2AB=4,连接BD交AF于点 G, 连接EG,当CF=1时, 求EG的长.
7. 如图1,在 Rt△ABC中,∠B=90°,AB=4,BC=2, 点 D、E 分别是边 BC、AC的中点, 连接DE. 将△CDE绕点 C逆时针方向旋转,记旋转角为α.
(1) 问题发现
①当α=0°时,
②当α=180°时,
(2) 拓展探究
试判断:当(0°≤α<360°时, 的大小有无变化 请仅就图2的情形给出证明.
(3) 问题解决
△CDE绕点 C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
8. 如图1,在钝角△ABC中,∠ABC=30°,AC=4, 点D为边AB中点, 点E为边BC中点, 将△BDE绕点B逆时针方向旋转α度 (0<α<180).
(1) 如图2, 当0<α<180时, 连接AD、CE.
求证: △BDA∽△BEC;
(2) 如图3, 直线CE、AD交于点 G. 在旋转过程中,∠AGC 的大小是否发生变化 如变化,请说明理由;如不变,请求出这个角的度数;
(3) 将△BDE从图1位置绕点 B 逆时针方向旋转180°,求点G的运动路程.
9.在△ABC中, CA=CB, ∠ACB=α. 点P是平面内不与点A、C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP, 连接AD、BD、CP.
(1) 观察猜想
如图1, 当α=60°时, 的值是 ,直线 BD 与直线CP相交所成的较小角的度数是 .
(2) 类比探究
如图2, α=90°时, 请写出: 的值及直线 BD 与直线 CP相交所成的较小角的度数,并就图2的情形说明理由.
(3) 解决问题
α=90°时, 若点E、F分别是CA、CB的中点, 点 P在直线EF 上,请直接写出点 C、P、D在同一直线上时 的值.
10.【问题背景】如图(1),已知△ABC∽△ADE, 求证: △ABD∽△ACE;
【尝试应用】如图(2), 在△ABC和△ADE中,∠BAC=∠DAE=90°, ∠ABC=∠ADE=30°, AC与DE相交于点 F, 点D在BC边上, 求 的值;
【拓展创新】如图(3),D是△ABC内一点,∠BAD=∠CBD=30°, ∠BDC=90°, AB=4, AC=2 , 直接写出 AD 的长.
11.在△ABC中, AB=AC, ∠BAC=α, 点P为线段CA 延长线上一动点,连接 PB,将线段 PB绕点 P逆时针旋转, 旋转角为α, 得到线段 PD, 连接DB、DC.
(1) 如图, 当α=60°时,
①求证: PA=DC;
②求∠DCP的度数;
(2)如图2, 当α=120°时, 直接写出 PA 和 DC 的数量关系.
(3)当α=120°时,若 请直接写出点D到 CP的距离为 .
12. 在△ABC中,∠ACB=90°,CD是中线,AC=BC, 一个以点 D 为顶点的45°角绕点 D 旋转, 使角的两边分别与 AC、BC 的延长线相交,交点分别为点 E、F,DF与AC交于点 M, DE与BC交于点N.
(1) 如图1, 若CE=CF, 求证: DE=DF;
(2) 如图 2, 在∠EDF 绕点 D 旋转的过程中, 试证明 CF 恒成立;
(3)若( 求DN的长.
13.在△ABC 中, AB=AC, ∠BAC=120°,以 CA 为边在∠ACB的另一侧作∠ACM=∠ACB, 点 D 为射线 BC上任意一点, 在射线 CM 上截取 CE=BD, 连接 AD、DE、AE.
(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;
(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立 如果成立,请给出证明; 如果不成立,请说明理由;
(3) 在 (2) 的条件下, 若AB=6, 求CF的最大值.
14.在Rt△ABC中, ∠ACB=90°, D是△ABC内一点, 连接AD、BD. 在BD左侧作Rt△BDE, 使∠BDE=90°, 以AD和DE为邻边作平行四边形ADEF, 连接CD、DF.
(1) 若AC=BC, BD=DE.
①如图1, 当B、D、F三点共线时, CD与DF之间的数量关系为 .
②如图2,当 B、D、F 三点不共线时,①中的结论是否仍然成立 请说明理由.
(2) 若BC=2AC, BD=2DE, CD= 且E、C、F三点共线,求 的值.
15. 将正方形ABCD的边AB绕点A 逆时针旋转至AB', 记旋转角为α, 连接BB', 过点D作DE 垂直于直线BB', 垂足为点E, 连接DB'、CE .
(1)如图1, 当α=60°时, △DEB'的形状为 , 连接BD, 可求出 '的值为 ;
(2) 当 且α≠90°时,
①(1) 中的两个结论是否仍然成立 如果成立,请仅就图2的情形进行证明; 如果不成立,请说明理由;②当以点B'、E、C、D为顶点的四边形是平行四边形时,请直接写出 的值.
1.
由题意可得: △CBD∽△CAE, 且
∴AE= , ∠CAE=∠CBD,
∴∠BAE=∠BAC+∠CAE=∠BAC+∠CBD=90°,
又∠CAF=∠CBD=∠CDE=60°,
∴△CFD∽△EFA,
的值为
2.
解析: 由题意得: △CEB≌△CFD, ∴BE=DF=6,连接BD, 则BD=10, ∴BF=8, ∴∠BFD=90°,∴△BOG∽△BFD,可得
3. 解析: (1) ∵点D是AB中点,
∴∠ACD=∠A=30°, ∴∠BDC=60°, ∴∠EDA=30°;
(2)∵∠CDE=∠FDG=90°,
∴∠FDG-∠CDG=∠CDE-∠CDG, 即∠CDF=∠EDG,
又∠CED=60°=∠DCF, ∴△CDF∽△EDG,
即
解析: (1) 相等, 垂直;
(2)成立, 如图2,连接AC, ∵BA=BC, 且∠ABC=60°, ∴
△ABC是等边三角形, ∴AB=AC, ∠BAC=60°,
∴∠BAC+∠CAP=∠PAE+∠CAP, 即∠BAP=∠CAE,在△APB和△AEC中,
∴△APB≌△AEC(SAS), ∴BP=CE, ∠ABP=∠ACE,又∠ABP=30°, ∴∠ACE=30°, ∴∠BCE=90°, ∴CE⊥BC,∴CE⊥AD.
(3) 连接CE交AD于点H, 则H是AD中点, CE⊥BC, 过点A作AO⊥BD交BD于点O,
则AO= , ∴OP=5, DP=2, ∴S△ADP= ×2× = ∴四边形ADPE的面积为8
解析: (1) △BEA≌△BFC.
∵∠ABC=60°=∠EBF, ∴∠ABC-∠EBC=∠EBF-∠EBC ,即∠ABE=∠CBF,在△BEA和△BFC中,
∴△BEA≌△BFC (SAS).
(2) ∵△BEA≌△BFC, ∴∠BAE=∠BCF, ∴∠BCF=60°,
∴CF∥AB,过点C作CH⊥AB交AB于点 H,∵AB=AC=2,
即 将 代入得: ∵△BEA≌△BFC, ∴AE=CF=
(3) 当点 E在AC延长线上时, △BEA≌△BFC 依然成立,
解析: (1) 相等.
(2)可证△ .
(3) 如图, 当点F在线段 CD上时, ∵AD=4, DF=1,
由题意可证得△AGB∽△FGD,
勾股定理得:
当点F在DC延长线上时,同理可求 综上,EG的长为 或
解析: (1) ,
不变, 可证得
(3) 当点E在线段AB上时,如下图所示:
由题意可证得△CDB∽△CEA, ∵CE= , BC=2, ∴BE=1,, ∴AE=3,
当点E在AB 延长线上时,
可得四边形 BCDE是矩形,
综上所述,BD的长为 或
8.解析:(1)∵D、E分别是BA、BC中点, 将△BDE旋转α可得∠DBA=∠EBC=α,∴△BDA∽△BEC.
(2) 不变. 由(1) 得△BDA∽△BEC, ∴∠BAD=∠BCE,由“8字”模型可得: ∠G=∠ABC=30°.
(3)∠G所对的边AC为定边,定边对定角,∴G点轨迹是个圆弧.以AC为边构造等边△AOC,点O即为圆心,AC=4,∴圆O半径为4. 通过起点和终点来确定轨迹,如图:
G点从B点出发, 当BD⊥BC时, 弧BG最长, 当旋转180°时,G点返回B点,∴点G的轨迹是弧BG长的2倍.
可得弧BG所对圆心角为 ∴G点轨迹长为
9解析: (1) △APC≌△ADB, ∴BD=CP, ∴BD=1.∠Q=∠CAB=60°.
(2) 由题意可得△ADB∽△APC, ∴DD=AD= BD 与CP所成的较小角是45°,如图所示,可用“8字”模型证明.
(3) 如下图, P、D、C共线, △APC是直角三角形,求 的值,但AD与 CP 并无位置关系,故可转化比例,考虑到 ,∴可转化为求 的值.
情况一: 过点P作MN⊥AB交BA 延长线于点N, 过点 C作CM⊥MN交MN于点 M.
不妨设AN=x,PN=y,△PNA∽△CMP,AMP=PN,代入得: 化简得: 解得: 考虑到点 P是MN中点, 则△ANP∽△APC,
情况二:如下图所示,同上可求,
综上所述, 的值为 或
10. 解析: (1) ∵△ABC∽△ADE, ∴AB=ACAE,
∠BAC-∠DAC=∠DAE-∠DAC, 即∠BAD=∠CAE,∴△ABD∽△ACE.
(2) 由题意可得△BAC∽△DAE, 连接CE,则△ADB∽△AEC, ∴∠ACE=∠ABC=30°, 可证△ADF∽△ 即 的值为3.
(3)过点D作DE⊥AD且. 可证△ADE∽△CDB, △ADC∽△EDB
又AB=4, ∴AE=2 , ∴AD= . ∴AD的长为
11. 解析: (1)①当α=60°时, △PBD、△BAC均是等边三角形, 可证△BAP≌△BCD, ∴PA=DC;
②∠BCD=∠BAP=120°, 又∠BCA=60°, ∴∠DCP=60°.
(2) 当α=120°时,
可证△BAC∽△BPD, 得△BPA∽△BDC,
(3)过点B作BH⊥CP交CP于点H,则 又BP= ,∴PH=2,∵△BPA∽△BDC,∴∠BPA=∠BDC,∴∠DCH=∠PBD=30°, 由 (2) 得
∵PA=5 或1, ∴ 或
∴点D到CP的距离为 或
解析:(1)由题意得△DCE≌△DCF(SAS),∴DE=DF.
(2)∵∠F+∠CDF=45°,∠CDE+∠CDF=45°,∴∠F=∠CDE,又∠DCF=∠DCE=135°,∴△FCD∽△DCE,∴CD=CD,∴ CD =CE·CF . ∴在∠EDF 绕点 D 旋转的过程中, CF恒成立.
(3)若CF= ,CD=2,则(CE=2 ,∴CE=CB,连接BE,则△BCE是等腰直角三角形, ∴BE=4, DE=2 易证 ∴DN的长为
解析: (1) 易证△ABD≌△ACE, ∴∠BAD=∠CAE,AD=AE, ∴∠BAD-∠CAD=∠CAE-∠CAD, 即∠BAC=∠DAE, ∴△ABC∽△ADE, ∴∠ADE=∠ABC=30°.
(2) 成立.
易证△ABD≌△ACE, 易证△ABC∽△ADE,∴∠ADE=∠ABC=30°.
(3) 求CF最大值,等价于求AF最小值.
∵∠ADF=∠ACD, ∴△AFD∽△ADC,
即AD =AF·AC, ∵AC=AB=6,
显然当AD⊥BC时, AD 取到最小值3, 此时 ∴CF的最大值为
解析:
由“8字”模型易证: ∠CBD=∠CAF,
连接CF, 易证△CDB≌△CFA, ∴CD=CF,且∠DCF=∠BCA=90°, ∴DF= CD.
②成立,类似还是证明△CDB≌△CFA,而其中关键性条件∠CBD=∠CAF与B、D、F共线与否比并无关系. BD与DE是垂直关系, 又AF∥DE, ∴BD⊥AF.
如下图, 延长BD与AF交于点 P, 则∠P=90°, 由“8字”模型可证: ∠CBD=∠CAF.
易证△CDB≌△CFA, ∴DF= CD.
(2) 延长BD与AF交于点P, 则BD⊥AF,
由“8 字”模型可得: ∠CBD=∠CAF, 又 BC=2AC,BD=2DE=2AF, ∴△CDB∽△CFA, ∴CD=2CF.
不妨设CD=4k, 则AC=5k,
,
解析:(1) 等腰直角三角形;
(2)①成立. 设∠ABB'=α, 则. ∠BAB'=180°-2α, ∴∠DAB'=90°-2α,
∴∠AB'D=45°+α, ∴∠EB'D=45°, 又∠B'ED=90 ,
∴△DEB'是等腰直角三角形.
连接BD,易证△EDC∽△B'DE, ∴BE=BD= ②如图,比值为1或3.
前言:旋转问题的探究题是近来中考题中的热点题型之一,此类问题一般从旋转的性质出发,探究旋转型全等与相似.
知 识 导 航
从全等到相似
在手拉手模型中,我们可以看成是两个相似的等腰三角形作共点旋转,由等腰条件可得一组全等三角形.
若△ABC与△ADE非等腰,则可得到旋转型相似.
以直角三角形为例:
如图, Rt△ABC∽Rt△ADE, 连接BD、CE.
可得:△ADB∽△AEC,且旋转的性质,旋转角都相等依然成立, 如下右图, ∠BAD=∠EAC=∠EFB.
引例1:如图,在Rt△ABC中,∠ACB=90°, BC=6,AC=8,点 D、E 分别是边AB、BC的中点, 连接DE, 将△BDE绕点 B 按顺时针方向旋转一定角度(小于 90°) 后,点D 的对应点D'和点 E 的对应点E'以及点 A 三个点在一直线上,连接CE', 则CE'= .
解析: ∵BE'=BE=3, AB=10,
又
由题意得: △BE'C∽△BD'A,
引例2:(1) 问题发现
如图1, 在△OAB和△OCD中, OA=OB, OC=OD,∠AOB=∠COD=40°, 连接AC, BD交于点 M. 填空: 的值为 ; ②∠AMB的度数为 .
(2) 类比探究
如图2, 在△OAB和△OCD中, ∠AOB=∠COD=90°,∠OAB=∠OCD=30°, 连接AC交BD的延长线于点 M.请判断 的值及∠AMB的度数,并说明理由;
(3) 拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC、BD所在直线交于点 M,若OD=1, OB= 请直接写出当点C与点 M重合时AC的长.
中小学教育资源及组卷应用平台
解析: (1) 由题意可证△AOC≌△BOD,
∴①∠CBD=1, ②∠AMB=∠AOB=40°.(旋转角都相等)
(2)∵∠AOB=∠COD=90°, ∠OAB=∠OCD=30°,
又∠AOC=90°+∠AOD=∠BOD, ∴△AOC∽△BOD,
∵∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=90°.
的值为 , ∠AMB的度数为90°.
(3) 如下左图, 可证△OCA∽△ODB, 设BD=x,则AC= x, ∵OD=1, ∴CD=2,
勾股定理: 解得: x=2,
如上右图, 由题意得: △OAC∽△OBD, 设BC=x,则 又. 解得: x=1, ∴AC=3 综上所述,AC的长为2 或3
真题演练
1.如图,两个大小不同的三角板放在同一平面内,直角顶点重合于点 C,点D在AB上,
∠BAC=∠DEC=30°, AC与DE交于点 F, 连接AE, 若BD=1, AD=5, 则
2. 如图,正方形ABCD的边长为5 ,点E是正方形ABCD内一点,将△BCE绕着点 C顺时针旋转90°,点E的对应点 F 和点 B、E在一条直线上,BF 与对角线 AC 相较于点G, 若DF=6, 则GF的长为 .
3. 如图, 在 Rt△ABC中, ∠ACB=90°,∠B=60°, D为AB边的中点, 连接DC过D作DE⊥DC交AC于点E.
(1) 求∠EDA的度数;
(2) 如图2, F为BC边上一点, 连接DF, 过D 作 DG⊥DF交AC于点G,请判断线段CF与EG的数量关系,并说明理由.
4.在菱形ABCD中, ∠ABC=60°, 点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点 P的位置变化而变化.
(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是 ,CE与AD的位置关系是 ;
(2) 当点 E在菱形ABCD外部时,(1)中的结论是否还成立 若成立,请予以证明; 若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);
(3) 如图4, 当点 P 在线段 BD 的延长线上时, 连接BE,若 求四边形ADPE的面积.
5.在数学兴趣小组活动中,小亮进行数学探究活动. △ABC是边长为2 的等边三角形,E是AC上一点,小亮以 BE为边向 BE 的右侧作等边三角形 BEF,连接CF.
(1)如图1,当点E在线段AC上时, EF、BC相交于点 D,小亮发现有两个三角形全等,请你找出来,并证明.
(2) 当点 E 在线段AC 上运动时,点F 也随着运动,若四边形ABFC的面积为 求AE的长.
(3)如图2, 当点E在AC的延长线上运动时, CF、BE相交于点D,请你探求△ECD的面积S 与△DBF的面积S 之间的数量关系. 并说明理由.
6. 如图, 在矩形ABCD中, AD=k·AB(k>0), 点 E 是线段 CB延长线上的一个动点, 连接AE,过点A作AF⊥AE交射线DC于点F.
(1)如图1,若k=1,则AF与AE之间的数量关系是 ;
(2)如图2, 若k≠1, 试判断AF 与AE 之间的数量关系,写出结论并证明;(用含k的式子表示)
(3)若AD=2AB=4,连接BD交AF于点 G, 连接EG,当CF=1时, 求EG的长.
7. 如图1,在 Rt△ABC中,∠B=90°,AB=4,BC=2, 点 D、E 分别是边 BC、AC的中点, 连接DE. 将△CDE绕点 C逆时针方向旋转,记旋转角为α.
(1) 问题发现
①当α=0°时,
②当α=180°时,
(2) 拓展探究
试判断:当(0°≤α<360°时, 的大小有无变化 请仅就图2的情形给出证明.
(3) 问题解决
△CDE绕点 C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
8. 如图1,在钝角△ABC中,∠ABC=30°,AC=4, 点D为边AB中点, 点E为边BC中点, 将△BDE绕点B逆时针方向旋转α度 (0<α<180).
(1) 如图2, 当0<α<180时, 连接AD、CE.
求证: △BDA∽△BEC;
(2) 如图3, 直线CE、AD交于点 G. 在旋转过程中,∠AGC 的大小是否发生变化 如变化,请说明理由;如不变,请求出这个角的度数;
(3) 将△BDE从图1位置绕点 B 逆时针方向旋转180°,求点G的运动路程.
9.在△ABC中, CA=CB, ∠ACB=α. 点P是平面内不与点A、C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP, 连接AD、BD、CP.
(1) 观察猜想
如图1, 当α=60°时, 的值是 ,直线 BD 与直线CP相交所成的较小角的度数是 .
(2) 类比探究
如图2, α=90°时, 请写出: 的值及直线 BD 与直线 CP相交所成的较小角的度数,并就图2的情形说明理由.
(3) 解决问题
α=90°时, 若点E、F分别是CA、CB的中点, 点 P在直线EF 上,请直接写出点 C、P、D在同一直线上时 的值.
10.【问题背景】如图(1),已知△ABC∽△ADE, 求证: △ABD∽△ACE;
【尝试应用】如图(2), 在△ABC和△ADE中,∠BAC=∠DAE=90°, ∠ABC=∠ADE=30°, AC与DE相交于点 F, 点D在BC边上, 求 的值;
【拓展创新】如图(3),D是△ABC内一点,∠BAD=∠CBD=30°, ∠BDC=90°, AB=4, AC=2 , 直接写出 AD 的长.
11.在△ABC中, AB=AC, ∠BAC=α, 点P为线段CA 延长线上一动点,连接 PB,将线段 PB绕点 P逆时针旋转, 旋转角为α, 得到线段 PD, 连接DB、DC.
(1) 如图, 当α=60°时,
①求证: PA=DC;
②求∠DCP的度数;
(2)如图2, 当α=120°时, 直接写出 PA 和 DC 的数量关系.
(3)当α=120°时,若 请直接写出点D到 CP的距离为 .
12. 在△ABC中,∠ACB=90°,CD是中线,AC=BC, 一个以点 D 为顶点的45°角绕点 D 旋转, 使角的两边分别与 AC、BC 的延长线相交,交点分别为点 E、F,DF与AC交于点 M, DE与BC交于点N.
(1) 如图1, 若CE=CF, 求证: DE=DF;
(2) 如图 2, 在∠EDF 绕点 D 旋转的过程中, 试证明 CF 恒成立;
(3)若( 求DN的长.
13.在△ABC 中, AB=AC, ∠BAC=120°,以 CA 为边在∠ACB的另一侧作∠ACM=∠ACB, 点 D 为射线 BC上任意一点, 在射线 CM 上截取 CE=BD, 连接 AD、DE、AE.
(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;
(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立 如果成立,请给出证明; 如果不成立,请说明理由;
(3) 在 (2) 的条件下, 若AB=6, 求CF的最大值.
14.在Rt△ABC中, ∠ACB=90°, D是△ABC内一点, 连接AD、BD. 在BD左侧作Rt△BDE, 使∠BDE=90°, 以AD和DE为邻边作平行四边形ADEF, 连接CD、DF.
(1) 若AC=BC, BD=DE.
①如图1, 当B、D、F三点共线时, CD与DF之间的数量关系为 .
②如图2,当 B、D、F 三点不共线时,①中的结论是否仍然成立 请说明理由.
(2) 若BC=2AC, BD=2DE, CD= 且E、C、F三点共线,求 的值.
15. 将正方形ABCD的边AB绕点A 逆时针旋转至AB', 记旋转角为α, 连接BB', 过点D作DE 垂直于直线BB', 垂足为点E, 连接DB'、CE .
(1)如图1, 当α=60°时, △DEB'的形状为 , 连接BD, 可求出 '的值为 ;
(2) 当 且α≠90°时,
①(1) 中的两个结论是否仍然成立 如果成立,请仅就图2的情形进行证明; 如果不成立,请说明理由;②当以点B'、E、C、D为顶点的四边形是平行四边形时,请直接写出 的值.
1.
由题意可得: △CBD∽△CAE, 且
∴AE= , ∠CAE=∠CBD,
∴∠BAE=∠BAC+∠CAE=∠BAC+∠CBD=90°,
又∠CAF=∠CBD=∠CDE=60°,
∴△CFD∽△EFA,
的值为
2.
解析: 由题意得: △CEB≌△CFD, ∴BE=DF=6,连接BD, 则BD=10, ∴BF=8, ∴∠BFD=90°,∴△BOG∽△BFD,可得
3. 解析: (1) ∵点D是AB中点,
∴∠ACD=∠A=30°, ∴∠BDC=60°, ∴∠EDA=30°;
(2)∵∠CDE=∠FDG=90°,
∴∠FDG-∠CDG=∠CDE-∠CDG, 即∠CDF=∠EDG,
又∠CED=60°=∠DCF, ∴△CDF∽△EDG,
即
解析: (1) 相等, 垂直;
(2)成立, 如图2,连接AC, ∵BA=BC, 且∠ABC=60°, ∴
△ABC是等边三角形, ∴AB=AC, ∠BAC=60°,
∴∠BAC+∠CAP=∠PAE+∠CAP, 即∠BAP=∠CAE,在△APB和△AEC中,
∴△APB≌△AEC(SAS), ∴BP=CE, ∠ABP=∠ACE,又∠ABP=30°, ∴∠ACE=30°, ∴∠BCE=90°, ∴CE⊥BC,∴CE⊥AD.
(3) 连接CE交AD于点H, 则H是AD中点, CE⊥BC, 过点A作AO⊥BD交BD于点O,
则AO= , ∴OP=5, DP=2, ∴S△ADP= ×2× = ∴四边形ADPE的面积为8
解析: (1) △BEA≌△BFC.
∵∠ABC=60°=∠EBF, ∴∠ABC-∠EBC=∠EBF-∠EBC ,即∠ABE=∠CBF,在△BEA和△BFC中,
∴△BEA≌△BFC (SAS).
(2) ∵△BEA≌△BFC, ∴∠BAE=∠BCF, ∴∠BCF=60°,
∴CF∥AB,过点C作CH⊥AB交AB于点 H,∵AB=AC=2,
即 将 代入得: ∵△BEA≌△BFC, ∴AE=CF=
(3) 当点 E在AC延长线上时, △BEA≌△BFC 依然成立,
解析: (1) 相等.
(2)可证△ .
(3) 如图, 当点F在线段 CD上时, ∵AD=4, DF=1,
由题意可证得△AGB∽△FGD,
勾股定理得:
当点F在DC延长线上时,同理可求 综上,EG的长为 或
解析: (1) ,
不变, 可证得
(3) 当点E在线段AB上时,如下图所示:
由题意可证得△CDB∽△CEA, ∵CE= , BC=2, ∴BE=1,, ∴AE=3,
当点E在AB 延长线上时,
可得四边形 BCDE是矩形,
综上所述,BD的长为 或
8.解析:(1)∵D、E分别是BA、BC中点, 将△BDE旋转α可得∠DBA=∠EBC=α,∴△BDA∽△BEC.
(2) 不变. 由(1) 得△BDA∽△BEC, ∴∠BAD=∠BCE,由“8字”模型可得: ∠G=∠ABC=30°.
(3)∠G所对的边AC为定边,定边对定角,∴G点轨迹是个圆弧.以AC为边构造等边△AOC,点O即为圆心,AC=4,∴圆O半径为4. 通过起点和终点来确定轨迹,如图:
G点从B点出发, 当BD⊥BC时, 弧BG最长, 当旋转180°时,G点返回B点,∴点G的轨迹是弧BG长的2倍.
可得弧BG所对圆心角为 ∴G点轨迹长为
9解析: (1) △APC≌△ADB, ∴BD=CP, ∴BD=1.∠Q=∠CAB=60°.
(2) 由题意可得△ADB∽△APC, ∴DD=AD= BD 与CP所成的较小角是45°,如图所示,可用“8字”模型证明.
(3) 如下图, P、D、C共线, △APC是直角三角形,求 的值,但AD与 CP 并无位置关系,故可转化比例,考虑到 ,∴可转化为求 的值.
情况一: 过点P作MN⊥AB交BA 延长线于点N, 过点 C作CM⊥MN交MN于点 M.
不妨设AN=x,PN=y,△PNA∽△CMP,AMP=PN,代入得: 化简得: 解得: 考虑到点 P是MN中点, 则△ANP∽△APC,
情况二:如下图所示,同上可求,
综上所述, 的值为 或
10. 解析: (1) ∵△ABC∽△ADE, ∴AB=ACAE,
∠BAC-∠DAC=∠DAE-∠DAC, 即∠BAD=∠CAE,∴△ABD∽△ACE.
(2) 由题意可得△BAC∽△DAE, 连接CE,则△ADB∽△AEC, ∴∠ACE=∠ABC=30°, 可证△ADF∽△ 即 的值为3.
(3)过点D作DE⊥AD且. 可证△ADE∽△CDB, △ADC∽△EDB
又AB=4, ∴AE=2 , ∴AD= . ∴AD的长为
11. 解析: (1)①当α=60°时, △PBD、△BAC均是等边三角形, 可证△BAP≌△BCD, ∴PA=DC;
②∠BCD=∠BAP=120°, 又∠BCA=60°, ∴∠DCP=60°.
(2) 当α=120°时,
可证△BAC∽△BPD, 得△BPA∽△BDC,
(3)过点B作BH⊥CP交CP于点H,则 又BP= ,∴PH=2,∵△BPA∽△BDC,∴∠BPA=∠BDC,∴∠DCH=∠PBD=30°, 由 (2) 得
∵PA=5 或1, ∴ 或
∴点D到CP的距离为 或
解析:(1)由题意得△DCE≌△DCF(SAS),∴DE=DF.
(2)∵∠F+∠CDF=45°,∠CDE+∠CDF=45°,∴∠F=∠CDE,又∠DCF=∠DCE=135°,∴△FCD∽△DCE,∴CD=CD,∴ CD =CE·CF . ∴在∠EDF 绕点 D 旋转的过程中, CF恒成立.
(3)若CF= ,CD=2,则(CE=2 ,∴CE=CB,连接BE,则△BCE是等腰直角三角形, ∴BE=4, DE=2 易证 ∴DN的长为
解析: (1) 易证△ABD≌△ACE, ∴∠BAD=∠CAE,AD=AE, ∴∠BAD-∠CAD=∠CAE-∠CAD, 即∠BAC=∠DAE, ∴△ABC∽△ADE, ∴∠ADE=∠ABC=30°.
(2) 成立.
易证△ABD≌△ACE, 易证△ABC∽△ADE,∴∠ADE=∠ABC=30°.
(3) 求CF最大值,等价于求AF最小值.
∵∠ADF=∠ACD, ∴△AFD∽△ADC,
即AD =AF·AC, ∵AC=AB=6,
显然当AD⊥BC时, AD 取到最小值3, 此时 ∴CF的最大值为
解析:
由“8字”模型易证: ∠CBD=∠CAF,
连接CF, 易证△CDB≌△CFA, ∴CD=CF,且∠DCF=∠BCA=90°, ∴DF= CD.
②成立,类似还是证明△CDB≌△CFA,而其中关键性条件∠CBD=∠CAF与B、D、F共线与否比并无关系. BD与DE是垂直关系, 又AF∥DE, ∴BD⊥AF.
如下图, 延长BD与AF交于点 P, 则∠P=90°, 由“8字”模型可证: ∠CBD=∠CAF.
易证△CDB≌△CFA, ∴DF= CD.
(2) 延长BD与AF交于点P, 则BD⊥AF,
由“8 字”模型可得: ∠CBD=∠CAF, 又 BC=2AC,BD=2DE=2AF, ∴△CDB∽△CFA, ∴CD=2CF.
不妨设CD=4k, 则AC=5k,
,
解析:(1) 等腰直角三角形;
(2)①成立. 设∠ABB'=α, 则. ∠BAB'=180°-2α, ∴∠DAB'=90°-2α,
∴∠AB'D=45°+α, ∴∠EB'D=45°, 又∠B'ED=90 ,
∴△DEB'是等腰直角三角形.
连接BD,易证△EDC∽△B'DE, ∴BE=BD= ②如图,比值为1或3.
同课章节目录
