2025年中考数学二轮专题复习 第2章 对称与旋转压轴题讲练第7节 手连心模型与对补四边形 (含解析)
文档属性
| 名称 | 2025年中考数学二轮专题复习 第2章 对称与旋转压轴题讲练第7节 手连心模型与对补四边形 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 330.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览




文档简介
第7节 手连心模型与对补四边形
前言:旋转本身或许并不难,难的是构造旋转,确定旋转的一个必要前提:邻边相等,再加入其它的料,会有不用的结果.
中小学教育资源及组卷应用平台
知识导航
1 手连心模型
(1)手连心模型:如图,正方形ABCD的对角线AC、BD交于点 E,以点 E为一顶点作正方形 EFGH, 其中 EF交AB边于点 M, EH交BC边于点N.
结论: EM=EN.
思路1: 可证△EMN≌△ENC(ASA), ∴EM=EN;
思路2: 可证△EMA≌△ENB (ASA), ∴EM=EN;
思路3: 过点E作EP⊥AB交AB于点 P, 作EQ⊥BC交BC于点 Q, 可证△EPM≌△EQN (ASA), ∴EM=EN.
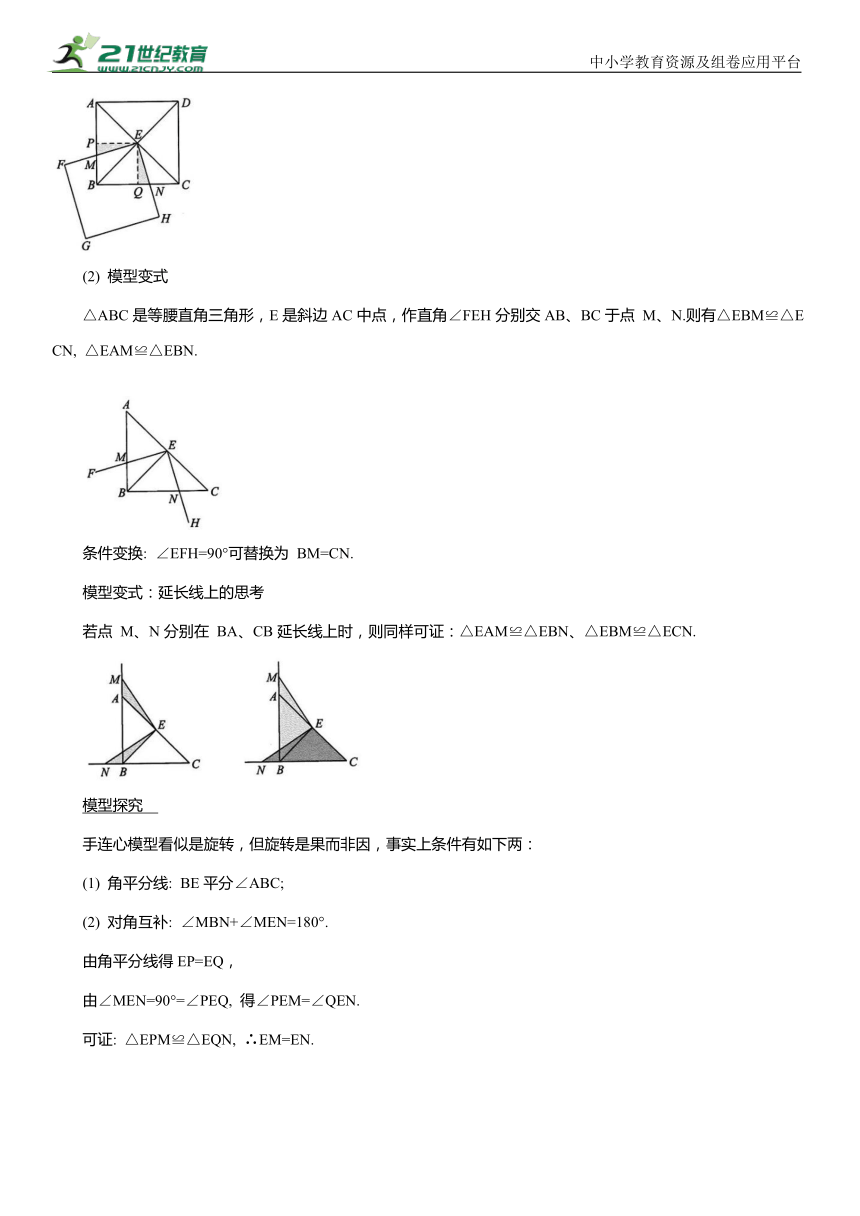
(2) 模型变式
△ABC是等腰直角三角形,E是斜边AC中点,作直角∠FEH分别交AB、BC于点 M、N.则有△EBM≌△ECN, △EAM≌△EBN.
条件变换: ∠EFH=90°可替换为 BM=CN.
模型变式:延长线上的思考
若点 M、N分别在 BA、CB延长线上时,则同样可证:△EAM≌△EBN、△EBM≌△ECN.
模型探究
手连心模型看似是旋转,但旋转是果而非因,事实上条件有如下两:
(1) 角平分线: BE平分∠ABC;
(2) 对角互补: ∠MBN+∠MEN=180°.
由角平分线得EP=EQ,
由∠MEN=90°=∠PEQ, 得∠PEM=∠QEN.
可证: △EPM≌△EQN, ∴EM=EN.
条件等价于:在四边形 EMBN中,
(1) 邻边相等: EM=EN,
(2) 对角互补: ∠MBN+∠MEN=180°.
即可构造旋转型全等: △EMB≌△ENB'.
引例1:如图,△ABC是⊙O的内接正三角形,点O是圆心, 点 D, E分别在边 AC, AB 上, 若DA=EB,则∠DOE的度数是 度.
解析: 连接OA、OB, 易证△OAD≌△OBE,∴∠DOE=∠AOB=120°, 即∠DOE的度数是120度.
对角互补四边形
如图, 在四边形 ABCD 中, AB=AD, ∠BAD+∠BCD=180°,则可将△ABC 绕点 A 旋转得△ADE, 其中 C、D、E 共线,且△ACE是等腰三角形.
AB=AD可得旋转后的重叠关系;
对角互补可得旋转后的共线关系.
特别地,
若∠BAD=90°, 则△ACE是等腰直角三角形,有
若∠BAD=60°, 则△ACE是等边三角形,有 CB+CD=CA.
一般地,若AB: AD: BD=a: a: b, 则可得a·(CB+CD)=b·CA
如若再去掉“邻边相等”,只有“对角互补”,这就是托勒密定理讨论的内容了
引例2: 已知, 在Rt△ABC中, ∠ABC=90°, AB=5, 以斜边AB 为边向外作正方形 ACDE, 连接AD、CE交于点 M, 连接BM, 若 则BC= .
解析:延长BC至点N使得CN=AB,易证△MAB≌△MCN,△BMN是等腰直角三角形,. 又CN=AB=5, ∴BC=7.
引例3:如图,是具有公共边AB 的两个直角三角形, 其中AC=BC, ∠ACB=∠ADB=90°.
(1)如图1,若延长DA到点E,使AE=BD,连接CD、CE.
①求证: CD=CE, CD⊥CE;
②求证:
(2) 若△ABC与△ABD位置如图2所示,请直接写出线段AD、BD、CD的数量关系.
解析: (1) 在△CBD和△CAE中,
∴△CDB≌△CAE(SAS),
∴CD=CE, ∠BCD=∠ACE,
∴∠DCE=∠ACD+∠ACE=∠ACD+∠BCD=∠ACB=90°.
∴CD=CE, CD⊥CE.
(2) 过点C作CE⊥CD交AD于点E,
∵∠ACB=∠DCE=90°, ∴∠BCD=∠ACE,
∵∠CBD+90°=∠CAE+90°,
∴∠CBD=∠CAE,
在△CDB和△CEA中,
∴△CDB≌△CEA(ASA)
∴BD+DE=AD,
又
∴AD、BD、CD的数量关系是:
其他结论
如图, 连接MN, 则.
真题演练
1.如图, 等边三角形 ABC 的边长为4, 点O是△ABC的中心, ∠FOG=120°, 绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论: ①OD=OE; ②S△ODE=S△BDE;③四边形 ODBE 的面积始终等于 ④△BDE 周长的最小值为6.上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
2. 如图, 在四边形ABCD中, AB=AD,∠BAD=∠BCD=90°, 连接AC, 若AC=6, 则四边形ABCD的面积为 .
3. 已知, 在△ABC中, ∠A=90°,AB=AC, 点D为BC的中点.
(1) 如图1, 若点E、F分别为AB、AC上的点,且DE⊥DF, 求证: BE=AF;
(2) 若点E、F分别为AB、CA延长线上的点, 且DE⊥DF, 那么BE=AF吗 请利用图2说明理由.
4. 定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.
根据以上定义,解决下列问题:
(1)如图1, 正方形ABCD中, E是CD上的点, 将△BCE绕B点旋转,使BC与BA重合,此时点E的对应点 F在 DA 的延长线上,则四边形 BEDF 为“直等补”四边形,为什么
(2) 如图2,已知四边形ABCD是“直等补”四边形,AB=BC=5, CD=1, AD>AB , 点 B 到直线 AD 的距离为BE. 求BE的长.
5. 在四边形ABCD中, ∠B+∠D=180°, 对角线AC平分∠BAD.
(1)如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB 与对角线AC的数量关系并说明理由.
(2) 如图2, 若将(1) 中的条件“∠B=90°”去掉,(1)中的结论是否成立 请说明理由.
(3)如图3, 若∠DAB=90°, 探究边AD、AB 与对角线AC的数量关系并说明理由.
6. (1)【探究发现】
如图1,∠EOF的顶点 O在正方形ABCD两条对角线的交点处, ∠EOF=90°, 将∠EOF绕点O旋转, 旋转过程中, ∠EOF 的两边分别与正方形ABCD的边 BC和CD交于点E和点F (点F与点 C, D 不重合). 则 CE、CF、BC之间满足的数量关系是 .
(2)【类比应用】
如图2,若将(1)中的“正方形ABCD”改为“∠BCD=120°的菱形ABCD”, 其他条件不变, 当∠EOF=60°时, 上述结论是否仍然成立 若成立,请给出证明; 若不成立,请猜想结论并说明理由.
(3)【拓展延伸】
如图3, OA平分∠BOD, 且OB>2OA,点C是OB上一点,∠CAD=60°,求OC的长.
7. 在△ABC中,∠C=90°, AC>BC, D是AB的中点. E为直线AC上一动点,连接DE. 过点D作DF⊥DE, 交直线BC于点F, 连接EF.
(1) 如图1, 当 E是线段 AC的中点时, 设AE=a, BF=b,求EF 的长(用含a,b的式子表示);
(2)当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE、EF、BF之间的数量关系,并证明.
8.感知: 如图1, AD平分∠BAC.
∠B+∠C=180°, ∠B=90°, 易知: DB=DC.
探究: 如图 2, AD 平分∠BAC, ∠ABD+∠ACD=180°,∠ABD<90°, 求证: DB=DC.
应用: 如图3,四边形ABCD中,∠B=45°,∠C=135°, DB=DC=a,则AB-AC= .(用含a的代数式表示)
9. 如图,已知∠MON=90°, OT是∠MON的平分线, A 是射线 OM 上一点, OA=8cm. 动点 P 从点 A 出发,以1cm/s的速度沿AO水平向左作匀速运动,与此同时,动点Q从点O出发,也以1cm/s的速度沿ON竖直向上作匀速运动. 连接PQ, 交OT于点B. 经过O、P、Q三点作圆,交 OT 于点 C, 连接 PC、QC. 设运动时间为 t(s), 其中0(1) 求OP+OQ的值;
(2) 是否存在实数t,使得线段 OB 的长度最大 若存在,求出t的值; 若不存在,说明理由.
(3) 求四边形OPCQ的面积.
从手连心模型到对补四边形
1.C.
连接OB、OC, 由题意得: △OBD≌△OCE,∴OD=OE, 结论①正确;
考虑∠FOG是可以旋转的,△ODE面积和△BDE面积并非始终相等,故结论②错误;
∵△OBD≌△OCE, ∴四边形ODBE的面积等于△OBC的面积, 故结论③正确;
考虑 BD=CE, ∴BD+BE=CE+BE=4, 只要DE最小,△BDE周长就最小,△ODE是顶角为120°的等腰三角形,故OD 最小, DE便最小, 当OD⊥AB时, OD取到最小值 此时 ∴周长最小值为6,故结论
④正确. 综上, 正确的有①③④, 选 C.
2.18.
解析: 延长 CB 至点 E 使得 BE=DC, 则△ADC≌△ABE, 即四边形ABCD的面积为18.
3. 解析: (1) 连接DA, 则DA⊥DB, ∵DE⊥DF,
∴∠BDE=∠ADF, 又∠B=∠DAF=45°, DB=DA,
∴△DEB≌△DFA, ∴BE=AF.
(2) 成立, ∵DB⊥DA, DE⊥DF, ∴∠BDE=∠ADF,又DB=DA, ∠DBE=135°=∠DAF, ∴△DBE≌△DAF,∴BE=AF.
解析:(1)由题意得:△BCE≌△BAF,∴∠CBE=∠ABF,BF=BF,又∠D=90°,∴四边形 BEDF为“直等补”四边形.
(2)延长DA至点F使得AF=CD,∵∠BAD+∠BCD=180°,∴∠BAF=∠BCD,又BA=BC, ∴△BAF≌△BCD(SAS), ∴BF=BD, ∠ABF=∠CBD,
∴∠ABF+∠ABD=∠CBD+∠ABD=90°,即△BDF是等腰直角三角形,连接AC,
∵BA=BC=5, ∴AC=5 , 又CD=1, ∴AD=7,
∴DF=AD+AF=AD+CD=8,
即BE的长为4.
解析: (1) AC=AB+AD.
由题意得:
延长AB至点E使得∠E=∠CAE,则∠CAD=∠E,CA=CE,∵∠D+∠ABC=180°,∴∠D=∠CBE,
∴∠ACD=∠ECB, ∵∠DAB=120°, ∴∠BCD=60°,
∴∠ACE=60°, ∴△ACE是等边三角形,
∴AC=AE=AB+BE=AB+AD, 即 AC=AB+AD.
(3) 同理可证△CDA≌△CBE, ∵∠DAB=90°,
∴∠DCB=90°, ∴∠ACE=∠DCB=90°,
即△ACE是等腰直角三角形,
即
解析: (1) BC=CE+CF.
(2)不成立,结论为
取BC中点G,连接OG,则(OG= BC=CG,∵∠BCD=120°,
∴∠BCO=60°, ∴△OGC是等边三角形,
∴OG=OC, ∠OGC=60°=∠OCF, ∵∠COG=∠EOF=60°,
∴∠EOG=∠COF, 在△OEG和△OFC中,
∴△OEG≌△OFC (ASA),
∴GE=CF, ∴CE+CF=CE+EG=CG= BC,即
(3) 过点A作AH⊥OB交OB于点 H,
设OH=x, 则.AH= x, BH=4-x,
在 Rt△AHB中, .
代入得:
解得: (舍), ∴OA=1,
过点A作AP⊥OD交OD于点 P, 则△AOH≌△AOP,
可证△AHC≌△APD,
7. 解析: (1) 由题意得CE=AE=a, BF=CF=b,
(2)作BG⊥BF交ED延长线于点G,可得△DAE≌△DBG,
∴AE=BG, ∵DF垂直平分EG, ∴EF=GF,
解析: (1) 过点 D 分别作 AB、AC 的垂线, 垂足分别记为M、N, 则由题意得DM=DN, ∵∠AMD=∠AND=90°, ∴∠MAN+∠MDN=180°, 又∠MAN+∠BDC=180°,
∴∠MDN=∠BDC, ∴∠BDM=∠CDN,
在△DMB 和△DNC中,
∴△DMB≌△DNC (ASA), ∴DB=DC.
连接 AD, 则 AD 平分∠BAC, 在 AB 上取点 E 使得AE=AC, 则△ACD≌△AED,
∴∠AED=∠ACD=135°,
∴∠BED=45°, △BED是等腰直角三角形,
解析: (1) 连接 CA, 易证△CQO≌△CPA, ∴OQ=AP,∴OP+OQ=OP+AP=OA=8cm, ∴OP+OQ的值为8cm.
(2)过点B作BH⊥OA交OA于点H,设BH=x,则OH=x, 可得 化简得: 当x=4时, x取到最大值2, 此时 OB 最大,OB的最大值是2 cm.
∴四边形OPCQ的面积为16.
前言:旋转本身或许并不难,难的是构造旋转,确定旋转的一个必要前提:邻边相等,再加入其它的料,会有不用的结果.
中小学教育资源及组卷应用平台
知识导航
1 手连心模型
(1)手连心模型:如图,正方形ABCD的对角线AC、BD交于点 E,以点 E为一顶点作正方形 EFGH, 其中 EF交AB边于点 M, EH交BC边于点N.
结论: EM=EN.
思路1: 可证△EMN≌△ENC(ASA), ∴EM=EN;
思路2: 可证△EMA≌△ENB (ASA), ∴EM=EN;
思路3: 过点E作EP⊥AB交AB于点 P, 作EQ⊥BC交BC于点 Q, 可证△EPM≌△EQN (ASA), ∴EM=EN.
(2) 模型变式
△ABC是等腰直角三角形,E是斜边AC中点,作直角∠FEH分别交AB、BC于点 M、N.则有△EBM≌△ECN, △EAM≌△EBN.
条件变换: ∠EFH=90°可替换为 BM=CN.
模型变式:延长线上的思考
若点 M、N分别在 BA、CB延长线上时,则同样可证:△EAM≌△EBN、△EBM≌△ECN.
模型探究
手连心模型看似是旋转,但旋转是果而非因,事实上条件有如下两:
(1) 角平分线: BE平分∠ABC;
(2) 对角互补: ∠MBN+∠MEN=180°.
由角平分线得EP=EQ,
由∠MEN=90°=∠PEQ, 得∠PEM=∠QEN.
可证: △EPM≌△EQN, ∴EM=EN.
条件等价于:在四边形 EMBN中,
(1) 邻边相等: EM=EN,
(2) 对角互补: ∠MBN+∠MEN=180°.
即可构造旋转型全等: △EMB≌△ENB'.
引例1:如图,△ABC是⊙O的内接正三角形,点O是圆心, 点 D, E分别在边 AC, AB 上, 若DA=EB,则∠DOE的度数是 度.
解析: 连接OA、OB, 易证△OAD≌△OBE,∴∠DOE=∠AOB=120°, 即∠DOE的度数是120度.
对角互补四边形
如图, 在四边形 ABCD 中, AB=AD, ∠BAD+∠BCD=180°,则可将△ABC 绕点 A 旋转得△ADE, 其中 C、D、E 共线,且△ACE是等腰三角形.
AB=AD可得旋转后的重叠关系;
对角互补可得旋转后的共线关系.
特别地,
若∠BAD=90°, 则△ACE是等腰直角三角形,有
若∠BAD=60°, 则△ACE是等边三角形,有 CB+CD=CA.
一般地,若AB: AD: BD=a: a: b, 则可得a·(CB+CD)=b·CA
如若再去掉“邻边相等”,只有“对角互补”,这就是托勒密定理讨论的内容了
引例2: 已知, 在Rt△ABC中, ∠ABC=90°, AB=5, 以斜边AB 为边向外作正方形 ACDE, 连接AD、CE交于点 M, 连接BM, 若 则BC= .
解析:延长BC至点N使得CN=AB,易证△MAB≌△MCN,△BMN是等腰直角三角形,. 又CN=AB=5, ∴BC=7.
引例3:如图,是具有公共边AB 的两个直角三角形, 其中AC=BC, ∠ACB=∠ADB=90°.
(1)如图1,若延长DA到点E,使AE=BD,连接CD、CE.
①求证: CD=CE, CD⊥CE;
②求证:
(2) 若△ABC与△ABD位置如图2所示,请直接写出线段AD、BD、CD的数量关系.
解析: (1) 在△CBD和△CAE中,
∴△CDB≌△CAE(SAS),
∴CD=CE, ∠BCD=∠ACE,
∴∠DCE=∠ACD+∠ACE=∠ACD+∠BCD=∠ACB=90°.
∴CD=CE, CD⊥CE.
(2) 过点C作CE⊥CD交AD于点E,
∵∠ACB=∠DCE=90°, ∴∠BCD=∠ACE,
∵∠CBD+90°=∠CAE+90°,
∴∠CBD=∠CAE,
在△CDB和△CEA中,
∴△CDB≌△CEA(ASA)
∴BD+DE=AD,
又
∴AD、BD、CD的数量关系是:
其他结论
如图, 连接MN, 则.
真题演练
1.如图, 等边三角形 ABC 的边长为4, 点O是△ABC的中心, ∠FOG=120°, 绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论: ①OD=OE; ②S△ODE=S△BDE;③四边形 ODBE 的面积始终等于 ④△BDE 周长的最小值为6.上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
2. 如图, 在四边形ABCD中, AB=AD,∠BAD=∠BCD=90°, 连接AC, 若AC=6, 则四边形ABCD的面积为 .
3. 已知, 在△ABC中, ∠A=90°,AB=AC, 点D为BC的中点.
(1) 如图1, 若点E、F分别为AB、AC上的点,且DE⊥DF, 求证: BE=AF;
(2) 若点E、F分别为AB、CA延长线上的点, 且DE⊥DF, 那么BE=AF吗 请利用图2说明理由.
4. 定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.
根据以上定义,解决下列问题:
(1)如图1, 正方形ABCD中, E是CD上的点, 将△BCE绕B点旋转,使BC与BA重合,此时点E的对应点 F在 DA 的延长线上,则四边形 BEDF 为“直等补”四边形,为什么
(2) 如图2,已知四边形ABCD是“直等补”四边形,AB=BC=5, CD=1, AD>AB , 点 B 到直线 AD 的距离为BE. 求BE的长.
5. 在四边形ABCD中, ∠B+∠D=180°, 对角线AC平分∠BAD.
(1)如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB 与对角线AC的数量关系并说明理由.
(2) 如图2, 若将(1) 中的条件“∠B=90°”去掉,(1)中的结论是否成立 请说明理由.
(3)如图3, 若∠DAB=90°, 探究边AD、AB 与对角线AC的数量关系并说明理由.
6. (1)【探究发现】
如图1,∠EOF的顶点 O在正方形ABCD两条对角线的交点处, ∠EOF=90°, 将∠EOF绕点O旋转, 旋转过程中, ∠EOF 的两边分别与正方形ABCD的边 BC和CD交于点E和点F (点F与点 C, D 不重合). 则 CE、CF、BC之间满足的数量关系是 .
(2)【类比应用】
如图2,若将(1)中的“正方形ABCD”改为“∠BCD=120°的菱形ABCD”, 其他条件不变, 当∠EOF=60°时, 上述结论是否仍然成立 若成立,请给出证明; 若不成立,请猜想结论并说明理由.
(3)【拓展延伸】
如图3, OA平分∠BOD, 且OB>2OA,点C是OB上一点,∠CAD=60°,求OC的长.
7. 在△ABC中,∠C=90°, AC>BC, D是AB的中点. E为直线AC上一动点,连接DE. 过点D作DF⊥DE, 交直线BC于点F, 连接EF.
(1) 如图1, 当 E是线段 AC的中点时, 设AE=a, BF=b,求EF 的长(用含a,b的式子表示);
(2)当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE、EF、BF之间的数量关系,并证明.
8.感知: 如图1, AD平分∠BAC.
∠B+∠C=180°, ∠B=90°, 易知: DB=DC.
探究: 如图 2, AD 平分∠BAC, ∠ABD+∠ACD=180°,∠ABD<90°, 求证: DB=DC.
应用: 如图3,四边形ABCD中,∠B=45°,∠C=135°, DB=DC=a,则AB-AC= .(用含a的代数式表示)
9. 如图,已知∠MON=90°, OT是∠MON的平分线, A 是射线 OM 上一点, OA=8cm. 动点 P 从点 A 出发,以1cm/s的速度沿AO水平向左作匀速运动,与此同时,动点Q从点O出发,也以1cm/s的速度沿ON竖直向上作匀速运动. 连接PQ, 交OT于点B. 经过O、P、Q三点作圆,交 OT 于点 C, 连接 PC、QC. 设运动时间为 t(s), 其中0
(2) 是否存在实数t,使得线段 OB 的长度最大 若存在,求出t的值; 若不存在,说明理由.
(3) 求四边形OPCQ的面积.
从手连心模型到对补四边形
1.C.
连接OB、OC, 由题意得: △OBD≌△OCE,∴OD=OE, 结论①正确;
考虑∠FOG是可以旋转的,△ODE面积和△BDE面积并非始终相等,故结论②错误;
∵△OBD≌△OCE, ∴四边形ODBE的面积等于△OBC的面积, 故结论③正确;
考虑 BD=CE, ∴BD+BE=CE+BE=4, 只要DE最小,△BDE周长就最小,△ODE是顶角为120°的等腰三角形,故OD 最小, DE便最小, 当OD⊥AB时, OD取到最小值 此时 ∴周长最小值为6,故结论
④正确. 综上, 正确的有①③④, 选 C.
2.18.
解析: 延长 CB 至点 E 使得 BE=DC, 则△ADC≌△ABE, 即四边形ABCD的面积为18.
3. 解析: (1) 连接DA, 则DA⊥DB, ∵DE⊥DF,
∴∠BDE=∠ADF, 又∠B=∠DAF=45°, DB=DA,
∴△DEB≌△DFA, ∴BE=AF.
(2) 成立, ∵DB⊥DA, DE⊥DF, ∴∠BDE=∠ADF,又DB=DA, ∠DBE=135°=∠DAF, ∴△DBE≌△DAF,∴BE=AF.
解析:(1)由题意得:△BCE≌△BAF,∴∠CBE=∠ABF,BF=BF,又∠D=90°,∴四边形 BEDF为“直等补”四边形.
(2)延长DA至点F使得AF=CD,∵∠BAD+∠BCD=180°,∴∠BAF=∠BCD,又BA=BC, ∴△BAF≌△BCD(SAS), ∴BF=BD, ∠ABF=∠CBD,
∴∠ABF+∠ABD=∠CBD+∠ABD=90°,即△BDF是等腰直角三角形,连接AC,
∵BA=BC=5, ∴AC=5 , 又CD=1, ∴AD=7,
∴DF=AD+AF=AD+CD=8,
即BE的长为4.
解析: (1) AC=AB+AD.
由题意得:
延长AB至点E使得∠E=∠CAE,则∠CAD=∠E,CA=CE,∵∠D+∠ABC=180°,∴∠D=∠CBE,
∴∠ACD=∠ECB, ∵∠DAB=120°, ∴∠BCD=60°,
∴∠ACE=60°, ∴△ACE是等边三角形,
∴AC=AE=AB+BE=AB+AD, 即 AC=AB+AD.
(3) 同理可证△CDA≌△CBE, ∵∠DAB=90°,
∴∠DCB=90°, ∴∠ACE=∠DCB=90°,
即△ACE是等腰直角三角形,
即
解析: (1) BC=CE+CF.
(2)不成立,结论为
取BC中点G,连接OG,则(OG= BC=CG,∵∠BCD=120°,
∴∠BCO=60°, ∴△OGC是等边三角形,
∴OG=OC, ∠OGC=60°=∠OCF, ∵∠COG=∠EOF=60°,
∴∠EOG=∠COF, 在△OEG和△OFC中,
∴△OEG≌△OFC (ASA),
∴GE=CF, ∴CE+CF=CE+EG=CG= BC,即
(3) 过点A作AH⊥OB交OB于点 H,
设OH=x, 则.AH= x, BH=4-x,
在 Rt△AHB中, .
代入得:
解得: (舍), ∴OA=1,
过点A作AP⊥OD交OD于点 P, 则△AOH≌△AOP,
可证△AHC≌△APD,
7. 解析: (1) 由题意得CE=AE=a, BF=CF=b,
(2)作BG⊥BF交ED延长线于点G,可得△DAE≌△DBG,
∴AE=BG, ∵DF垂直平分EG, ∴EF=GF,
解析: (1) 过点 D 分别作 AB、AC 的垂线, 垂足分别记为M、N, 则由题意得DM=DN, ∵∠AMD=∠AND=90°, ∴∠MAN+∠MDN=180°, 又∠MAN+∠BDC=180°,
∴∠MDN=∠BDC, ∴∠BDM=∠CDN,
在△DMB 和△DNC中,
∴△DMB≌△DNC (ASA), ∴DB=DC.
连接 AD, 则 AD 平分∠BAC, 在 AB 上取点 E 使得AE=AC, 则△ACD≌△AED,
∴∠AED=∠ACD=135°,
∴∠BED=45°, △BED是等腰直角三角形,
解析: (1) 连接 CA, 易证△CQO≌△CPA, ∴OQ=AP,∴OP+OQ=OP+AP=OA=8cm, ∴OP+OQ的值为8cm.
(2)过点B作BH⊥OA交OA于点H,设BH=x,则OH=x, 可得 化简得: 当x=4时, x取到最大值2, 此时 OB 最大,OB的最大值是2 cm.
∴四边形OPCQ的面积为16.
同课章节目录
