2025年中考数学二轮专题复习 第4章 圆 压轴题讲练第3节 动圆相切 (二) (含解析)
文档属性
| 名称 | 2025年中考数学二轮专题复习 第4章 圆 压轴题讲练第3节 动圆相切 (二) (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 369.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览




文档简介
第3节 动圆相切 (二)
前言:本节讨论关于动圆相切的另类问题:(1) 直线与圆交点个数的分析;(2) 动圆相切构造最值. 动圆相切不仅仅是类题型,也可以是某些最值问题的方法.
知 识 导 航
交点个数的分析
圆与线段或图形交点个数问题,考虑交点个数变化的位置,当:①圆与线段相切、②圆过线段端点时,交点个数会发生改变.确定整个运动过程中的所有特殊位置是解题关键.
引例1:如图,在坐标系中,点A坐标为(1,0),点B坐标为(0,3), 以点P(m,0)(m<0)为圆心, 4为半径作圆,若⊙P与线段AB只有1个交点,求m的取值范围.
解析: 考虑⊙P与AB 相切: 过点 P作 PH⊥AB,
当PH=4时, ⊙P与AB相切,
由题意得:△PHA∽△BOA, ∴PA=4
即
当⊙P过点A时, m=-3;
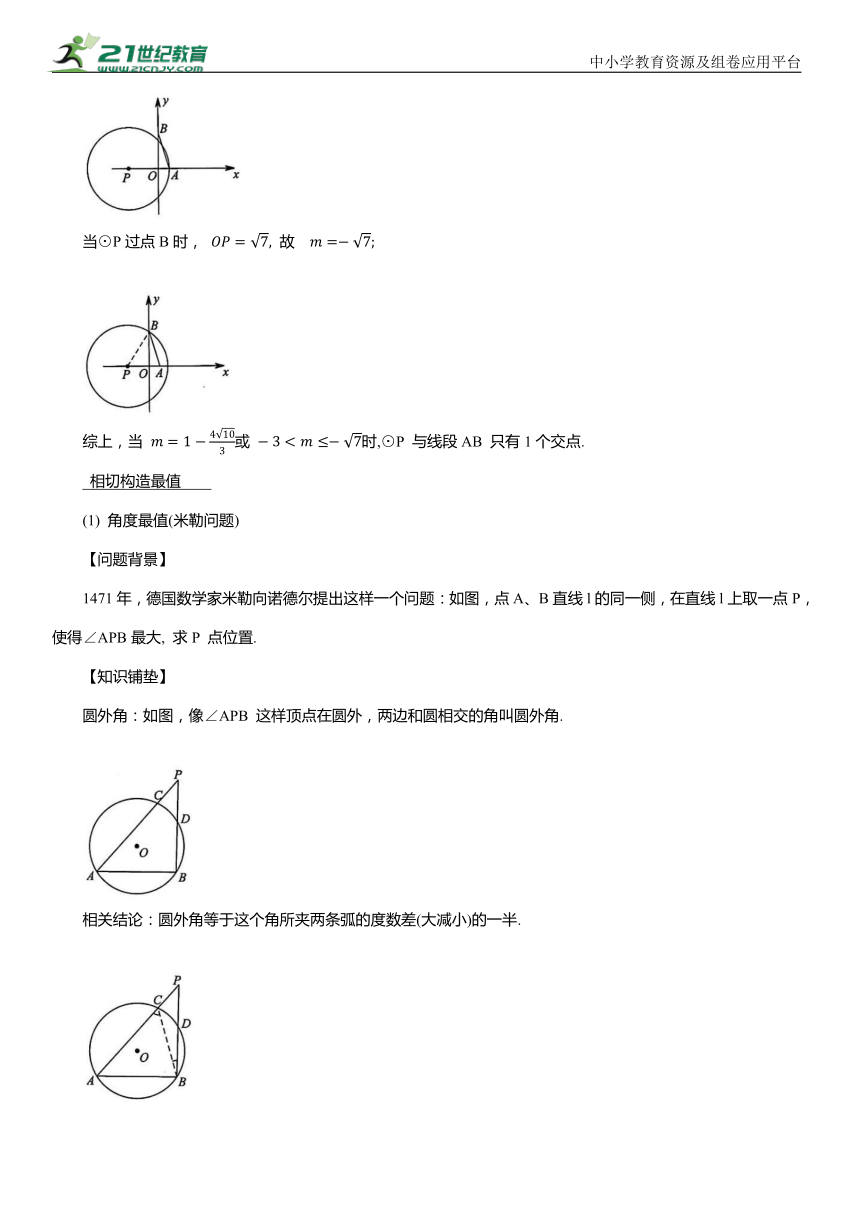
当⊙P过点B时, 故
综上,当 或 时,⊙P 与线段AB 只有1个交点.
相切构造最值
(1) 角度最值(米勒问题)
【问题背景】
1471年,德国数学家米勒向诺德尔提出这样一个问题:如图,点A、B直线l的同一侧,在直线l上取一点P,使得∠APB最大, 求P 点位置.
中小学教育资源及组卷应用平台
【知识铺垫】
圆外角:如图,像∠APB 这样顶点在圆外,两边和圆相交的角叫圆外角.
相关结论:圆外角等于这个角所夹两条弧的度数差(大减小)的一半.
如图,
换句话说,对同一个圆而言,同弧所对的圆周角>圆外角.
问题结论
结论: 当点 P 不与A、B 共线时, 作△PAB 的外接圆, 当圆与直线l相切时,∠APB 最大.
证明:在直线l上任取一点 M (不与点 P重合),连接AM、BM, ∠AMB 即为⊙O的圆外角,
∴∠APB>∠AMB, ∠APB 最大.
∴当圆与直线l相切时,∠APB 最大.
特别地,若点A、B与P分别在一个角的两边,如下图,则有 (切割线定理)
证明: ∵∠POA=∠BOP, ∠OPA=∠OBP (弦切角定理) 即可通过OA、OB线段长确定 OP 长,便知P 点位置.
引例2: 如图, 在平面直角坐标系中, A(1, 0)、B(5,0)直线l经过点 C(-1,2),点P是直线l上的动点,若∠APB的最大值为45°,求直线l的解析式.
解析:考虑到直线l 未知但∠APB 的最大值已知为 45°,可构造圆. 记△ABP 外接圆圆心为 M 点,
则∠AMB=2∠APB=90°, ∴可确定 M点位置.
根据A(1, 0)、B(5, 0), 可得M点坐标为(3, 2),连接MC、MP, ∵⊙M与直线CP 相切,
∴MP⊥CP, △CPM是直角三角形.
∵MC=4, MP=MA=2
即△CPM是等腰直角三角形,
可得P 点坐标为(1, 4),
又C点坐标为(-1, 2),
∴直线l的解析式为y=x+3.
(2) 线段最值
引例3:如图, 在 Rt△ABC中, ∠ABC 是直角, AB=3, BC=4, P是 BC边上的动点, 设BP=x, 若能在AC 边上找到一点 Q, 使∠BQP=90°, 则 x 的取值范围是
解析: 点Q满足∠BQP=90°,则以BP为直径作圆,与AC边交点即为点Q,存在这样的点Q即圆与AC有交点. 求x的取值范围即分别确定BP 的最大值和最小值.
当圆与AC相切时,BP 最小,
圆心记为点 O, 连接OQ, 则OQ=OB,
由 得
当点P与点 C重合时,BP最大,最大值为4,故x的取值范围是3≤x≤4.
真 题 演 练
1. 如图, 在矩形 ABCD 中, AB=6,BC=8,动点Q从点A出发,沿着AB方向以1个单位长度/秒的速度匀速运动,同时动点 P从点 B 出发,沿着对角线BD方向也以1 个单位长度/秒的速度匀速运动,设运动时间为t秒(0(1) 填空: FB= (用t的代数式表示);
(2) 当t为何值时,点Q与点F相遇
(3) 当线段 QE 与⊙P 有两个公共点时,求t 的取值范围.
2. 如图,在平面直角坐标系中,O为坐标原点, 点A、B的坐标分别为(8, 0)、(0, 6). 动点Q从点O、动点 P从点A 同时出发,分别沿着OA方向、AB 方向均以 1 个单位长度/秒的速度匀速运动,运动时间为 t(秒)(0(1) 求当t为何值时,点Q与点D 重合
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC 只有一个交点,请直接写出t的取值范围.
3. 如图1 和 2, 在平行四边形 ABCD 中, 点 P 为AB 延长线上一点,过点A作⊙O切CP于点 P, 设BP=x.
(1)如图1, x为何值时, 圆心O落在 AP上 若此时⊙O交AD于点E,直接指出 PE与BC的位置关系;
(2)当x=4时, 如图2, ⊙O与AC交于点Q, 求∠CAP的度数,并通过计算比较弦 AP 与劣弧PQ长度的大小;
(3)当⊙O与线段AD只有一个公共点时,直接写出x的取值范围.
4. 如图, 菱形ABCD的边长为2cm,∠DAB=60°. 点 P 从 A 点出发, 以 的速度, 沿 AC向C作匀速运动; 与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB 作匀速运动. 当P 运动到 C 点时,P、Q都停止运动. 设点 P 运动的时间为 ts.
(1) 当P异于A、C时, 请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P 与边 BC分别有1个公共点和2个公共点
5. 如图1,平行四边形ABCD中,AB⊥AC,AB=6, AD=10, 点 P 在边 AD 上运动, 以 P 为圆心, PA为半径的⊙P与对角线AC交于A、E两点.
(1) 如图2, 当⊙P 与边 CD相切于点F时, 求AP的长;
(2)不难发现,当⊙P 与边CD相切时,⊙P 与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P 与平行四边形 ABCD 的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .
6. 如图, 在 Rt△ABC中, ∠ACB=90°, ∠B=30°, AB=4, D是BC上一动点, CE⊥AD于E, EF⊥AB 交BC于点 F, 则CF 的最大值是 .
7. 如图 1, 在等腰直角△ADC 中, ∠ADC=90°, AD=4. 点E是AD的中点, 以DE为边作正方形DEFG, 连接AG、CE. 将正方形DEFG绕点D顺时针旋转,旋转角为( 延长CE交直线AG于点P,在旋转过程中,线段 PC长的最大值是 .
8.如图, 抛物线 与x轴交于A(-1, 0)、B两点, 与y轴交于点C, 过点 C作CD⊥y轴交抛物线于另一点 D,作DE⊥x轴,垂足为点E,双曲线 经过点 D, 连接BD.
(1) 求抛物线的表达式;
(2)动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大 (请直接写出结果)
9. 如图,在直角坐标系中,四边形OABC是平行四边形, 经过 A (-2, 0)、B、C三点的抛物线 与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点 E.
(1) 求这条抛物线对应的函数表达式;
(2) 已知 P 是抛物线对称轴上的点,满足在直线 MD 上存在唯一的点 Q, 使得∠PQE=45°, 求点 P的坐标.
第3节 动圆相切(二)
1.解析:
(2)AQ=t,若点Q与点F相遇,则AQ+BF=6,
即 解得:
故t为 时,点Q与点F相遇.
(3)考虑何时QE与圆P相切,即当QE⊥BD时,
又BQ=6-t, BE=2t, 代入得: 解得: 从相切开始,至点Q与点F重合,有2个交点,故t的取值范围是
2解析: 若点Q与点D重合,则(OQ+AQ=8,即 解得:
(2)当 时,
当 时,
则
综上,
当t=5时, S的最大值为15.
(3)1个交点:在CQ与圆P相切及之前,在 Q、D相遇之后, 解得:
当 或 时, 圆 P 与线段 QC 只有 1 个交点.
3. 解析:( ∴PC=12, PB=9, ∴x的值为9时, 点O落在AP 上.此时PE⊥BC, ∵PE⊥AD, AD∥BC, ∴可得PE⊥BC.
(2) 过点C作CH⊥AP交AP于点 H, 设PH=x,
则
∴AH=3+12=15, ∴AH=CH, ∴∠CAP=45°.
过点O作ON⊥AP交AP于点N, 则 易证△PNO∽△CHP, 又PH=5, CH=12, ∴CP=13, 代入得: 解得:
∴弦AP长度大于弧PQ长度.
(3) x≥18.
当 BP=18时, 圆O与DA 相切, 当BP>18时, 圆O与AD边只有一个交点A.
4解析: (1) 由题意得:
∴△APQ∽△ACB, ∴∠APQ=∠ACB, ∴PQ∥BC.
(2) 当圆P与BC相切时,有1个公共点,
当圆P过点B时,圆P与BC边有2个交点,此时△PBQ是等边三角形,点P为AC中点,
当圆P过点C时, 解得: 则
当点P与点C重合时,圆P与BC边有1个交点,此时t=2;
综上所述,当 或 或 t=2 时, 圆 P 与BC边有1个交点;
当 时,圆P与BC有2个交点.
5解析: (1) 连接PF, 则PF⊥CD, 且PA=PF,
设 PA=x, 则
解得: ∴AP的长为409.
(2) 从圆P与CD边相切开始,有4个交点,直到圆 P与BC边相切于点 M,
此时PM⊥BC, 易求
之后交点个数大于4,直到如下图,圆P过点D,则过点C,且与BC边有1交点,
此时
综上所述,公共点个数为4时, 或.AP=5.
6解析: ∠AEC=90°且 AC为定值, 故 E 点轨迹是以AC 为直径的圆弧. 考虑 EF⊥AB, 且E 点在圆上, 故当 EF与圆相切的时候,CF取到最大值.连接OF,易证△OCF≌△OEF,
7解析:
由题意可得∠APC=90°,∵AC为定值,∴当∠ACP最小时,CP长最大,由旋转可知E点轨迹是以点D为圆心的圆,当CP 与圆 D 相切时∠PCD 最大, 即∠PCA 最小, ∵DE=2,DC=4, ∴CE=2 又 EP=ED=2, ∴PC 长的最大值为
8.解析:(1) 考虑到点D纵坐标与点C相同,为3,代入反比例解析式,可得D点坐标为(2,3),根据A、D坐标可得抛物线解析式:
(2) 求t即求P 点位置.
思路1:作外接圆.
作过点B、D的圆且与y轴相切时,切点即为所求P点,考虑到本题只要直接写出结果即可,所以做法只要做对就可.由抛物线解析式可得 B 点坐标为(3, 0),结合 D (2, 3),则BD中点N坐标为
作BD的垂直平分线,即过N点作BD的垂线,
利用 可求得垂直平分线解析式为
三角形 PBD 圆心记为Q, 点Q 在 BD 垂直平分线上, 设Q点坐标为
根据QP=QB, 可得:
解得: (舍)
故Q点坐标为 P点坐标为 所以t的值为
思路2:切割线定理
延长BD交y轴于 M点,当 ·MB 时, ∠BPD 最大.
考虑到B(3,0)、D(2,3),可得直线BD解析式: y=-3x+9,故直线BD与y轴交点 M点坐标为(0, 9),
∴P点坐标为
故t的值为
9解析:(1)由题意得BC=AO=2, BC∥AO, ∴C点坐标为(2, ),设解析式为. 将点 A 坐标代入,解得: ∴抛物线的表达式为
(2)由题意得顶点M坐标为(1,3),令 解得: ∴D点坐标是 (4, 0).
①当点 P线段 EM上时,以PE为斜边在对称轴右侧作等腰直角△PNE,以N为圆心、PN为半径作圆,与MD 相切时,切点即唯一的点Q, 满足∠PQE=45°. ∵△MED是等腰直角三角形,∴点Q为MD中点,∴点Q坐标为( , ),对应P点坐标为(1, ).
②当点 P在M点处时, 过点 E作 EN⊥PD, 则△PEN是等腰直角三角形,以点N为圆心,PN 为半径作圆,过点 D,此时∠PDE=45°, 点 D 即满足条件的点Q, 对应P 点坐标为(1, 3)
③当点P在x轴下方抛物线上时,可得点P坐标为(1,-3).
综上, P 点坐标为(1, ) 或(1, 3) 或(1, - 3).
前言:本节讨论关于动圆相切的另类问题:(1) 直线与圆交点个数的分析;(2) 动圆相切构造最值. 动圆相切不仅仅是类题型,也可以是某些最值问题的方法.
知 识 导 航
交点个数的分析
圆与线段或图形交点个数问题,考虑交点个数变化的位置,当:①圆与线段相切、②圆过线段端点时,交点个数会发生改变.确定整个运动过程中的所有特殊位置是解题关键.
引例1:如图,在坐标系中,点A坐标为(1,0),点B坐标为(0,3), 以点P(m,0)(m<0)为圆心, 4为半径作圆,若⊙P与线段AB只有1个交点,求m的取值范围.
解析: 考虑⊙P与AB 相切: 过点 P作 PH⊥AB,
当PH=4时, ⊙P与AB相切,
由题意得:△PHA∽△BOA, ∴PA=4
即
当⊙P过点A时, m=-3;
当⊙P过点B时, 故
综上,当 或 时,⊙P 与线段AB 只有1个交点.
相切构造最值
(1) 角度最值(米勒问题)
【问题背景】
1471年,德国数学家米勒向诺德尔提出这样一个问题:如图,点A、B直线l的同一侧,在直线l上取一点P,使得∠APB最大, 求P 点位置.
中小学教育资源及组卷应用平台
【知识铺垫】
圆外角:如图,像∠APB 这样顶点在圆外,两边和圆相交的角叫圆外角.
相关结论:圆外角等于这个角所夹两条弧的度数差(大减小)的一半.
如图,
换句话说,对同一个圆而言,同弧所对的圆周角>圆外角.
问题结论
结论: 当点 P 不与A、B 共线时, 作△PAB 的外接圆, 当圆与直线l相切时,∠APB 最大.
证明:在直线l上任取一点 M (不与点 P重合),连接AM、BM, ∠AMB 即为⊙O的圆外角,
∴∠APB>∠AMB, ∠APB 最大.
∴当圆与直线l相切时,∠APB 最大.
特别地,若点A、B与P分别在一个角的两边,如下图,则有 (切割线定理)
证明: ∵∠POA=∠BOP, ∠OPA=∠OBP (弦切角定理) 即可通过OA、OB线段长确定 OP 长,便知P 点位置.
引例2: 如图, 在平面直角坐标系中, A(1, 0)、B(5,0)直线l经过点 C(-1,2),点P是直线l上的动点,若∠APB的最大值为45°,求直线l的解析式.
解析:考虑到直线l 未知但∠APB 的最大值已知为 45°,可构造圆. 记△ABP 外接圆圆心为 M 点,
则∠AMB=2∠APB=90°, ∴可确定 M点位置.
根据A(1, 0)、B(5, 0), 可得M点坐标为(3, 2),连接MC、MP, ∵⊙M与直线CP 相切,
∴MP⊥CP, △CPM是直角三角形.
∵MC=4, MP=MA=2
即△CPM是等腰直角三角形,
可得P 点坐标为(1, 4),
又C点坐标为(-1, 2),
∴直线l的解析式为y=x+3.
(2) 线段最值
引例3:如图, 在 Rt△ABC中, ∠ABC 是直角, AB=3, BC=4, P是 BC边上的动点, 设BP=x, 若能在AC 边上找到一点 Q, 使∠BQP=90°, 则 x 的取值范围是
解析: 点Q满足∠BQP=90°,则以BP为直径作圆,与AC边交点即为点Q,存在这样的点Q即圆与AC有交点. 求x的取值范围即分别确定BP 的最大值和最小值.
当圆与AC相切时,BP 最小,
圆心记为点 O, 连接OQ, 则OQ=OB,
由 得
当点P与点 C重合时,BP最大,最大值为4,故x的取值范围是3≤x≤4.
真 题 演 练
1. 如图, 在矩形 ABCD 中, AB=6,BC=8,动点Q从点A出发,沿着AB方向以1个单位长度/秒的速度匀速运动,同时动点 P从点 B 出发,沿着对角线BD方向也以1 个单位长度/秒的速度匀速运动,设运动时间为t秒(0
(2) 当t为何值时,点Q与点F相遇
(3) 当线段 QE 与⊙P 有两个公共点时,求t 的取值范围.
2. 如图,在平面直角坐标系中,O为坐标原点, 点A、B的坐标分别为(8, 0)、(0, 6). 动点Q从点O、动点 P从点A 同时出发,分别沿着OA方向、AB 方向均以 1 个单位长度/秒的速度匀速运动,运动时间为 t(秒)(0
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC 只有一个交点,请直接写出t的取值范围.
3. 如图1 和 2, 在平行四边形 ABCD 中, 点 P 为AB 延长线上一点,过点A作⊙O切CP于点 P, 设BP=x.
(1)如图1, x为何值时, 圆心O落在 AP上 若此时⊙O交AD于点E,直接指出 PE与BC的位置关系;
(2)当x=4时, 如图2, ⊙O与AC交于点Q, 求∠CAP的度数,并通过计算比较弦 AP 与劣弧PQ长度的大小;
(3)当⊙O与线段AD只有一个公共点时,直接写出x的取值范围.
4. 如图, 菱形ABCD的边长为2cm,∠DAB=60°. 点 P 从 A 点出发, 以 的速度, 沿 AC向C作匀速运动; 与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB 作匀速运动. 当P 运动到 C 点时,P、Q都停止运动. 设点 P 运动的时间为 ts.
(1) 当P异于A、C时, 请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P 与边 BC分别有1个公共点和2个公共点
5. 如图1,平行四边形ABCD中,AB⊥AC,AB=6, AD=10, 点 P 在边 AD 上运动, 以 P 为圆心, PA为半径的⊙P与对角线AC交于A、E两点.
(1) 如图2, 当⊙P 与边 CD相切于点F时, 求AP的长;
(2)不难发现,当⊙P 与边CD相切时,⊙P 与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P 与平行四边形 ABCD 的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .
6. 如图, 在 Rt△ABC中, ∠ACB=90°, ∠B=30°, AB=4, D是BC上一动点, CE⊥AD于E, EF⊥AB 交BC于点 F, 则CF 的最大值是 .
7. 如图 1, 在等腰直角△ADC 中, ∠ADC=90°, AD=4. 点E是AD的中点, 以DE为边作正方形DEFG, 连接AG、CE. 将正方形DEFG绕点D顺时针旋转,旋转角为( 延长CE交直线AG于点P,在旋转过程中,线段 PC长的最大值是 .
8.如图, 抛物线 与x轴交于A(-1, 0)、B两点, 与y轴交于点C, 过点 C作CD⊥y轴交抛物线于另一点 D,作DE⊥x轴,垂足为点E,双曲线 经过点 D, 连接BD.
(1) 求抛物线的表达式;
(2)动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大 (请直接写出结果)
9. 如图,在直角坐标系中,四边形OABC是平行四边形, 经过 A (-2, 0)、B、C三点的抛物线 与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点 E.
(1) 求这条抛物线对应的函数表达式;
(2) 已知 P 是抛物线对称轴上的点,满足在直线 MD 上存在唯一的点 Q, 使得∠PQE=45°, 求点 P的坐标.
第3节 动圆相切(二)
1.解析:
(2)AQ=t,若点Q与点F相遇,则AQ+BF=6,
即 解得:
故t为 时,点Q与点F相遇.
(3)考虑何时QE与圆P相切,即当QE⊥BD时,
又BQ=6-t, BE=2t, 代入得: 解得: 从相切开始,至点Q与点F重合,有2个交点,故t的取值范围是
2解析: 若点Q与点D重合,则(OQ+AQ=8,即 解得:
(2)当 时,
当 时,
则
综上,
当t=5时, S的最大值为15.
(3)1个交点:在CQ与圆P相切及之前,在 Q、D相遇之后, 解得:
当 或 时, 圆 P 与线段 QC 只有 1 个交点.
3. 解析:( ∴PC=12, PB=9, ∴x的值为9时, 点O落在AP 上.此时PE⊥BC, ∵PE⊥AD, AD∥BC, ∴可得PE⊥BC.
(2) 过点C作CH⊥AP交AP于点 H, 设PH=x,
则
∴AH=3+12=15, ∴AH=CH, ∴∠CAP=45°.
过点O作ON⊥AP交AP于点N, 则 易证△PNO∽△CHP, 又PH=5, CH=12, ∴CP=13, 代入得: 解得:
∴弦AP长度大于弧PQ长度.
(3) x≥18.
当 BP=18时, 圆O与DA 相切, 当BP>18时, 圆O与AD边只有一个交点A.
4解析: (1) 由题意得:
∴△APQ∽△ACB, ∴∠APQ=∠ACB, ∴PQ∥BC.
(2) 当圆P与BC相切时,有1个公共点,
当圆P过点B时,圆P与BC边有2个交点,此时△PBQ是等边三角形,点P为AC中点,
当圆P过点C时, 解得: 则
当点P与点C重合时,圆P与BC边有1个交点,此时t=2;
综上所述,当 或 或 t=2 时, 圆 P 与BC边有1个交点;
当 时,圆P与BC有2个交点.
5解析: (1) 连接PF, 则PF⊥CD, 且PA=PF,
设 PA=x, 则
解得: ∴AP的长为409.
(2) 从圆P与CD边相切开始,有4个交点,直到圆 P与BC边相切于点 M,
此时PM⊥BC, 易求
之后交点个数大于4,直到如下图,圆P过点D,则过点C,且与BC边有1交点,
此时
综上所述,公共点个数为4时, 或.AP=5.
6解析: ∠AEC=90°且 AC为定值, 故 E 点轨迹是以AC 为直径的圆弧. 考虑 EF⊥AB, 且E 点在圆上, 故当 EF与圆相切的时候,CF取到最大值.连接OF,易证△OCF≌△OEF,
7解析:
由题意可得∠APC=90°,∵AC为定值,∴当∠ACP最小时,CP长最大,由旋转可知E点轨迹是以点D为圆心的圆,当CP 与圆 D 相切时∠PCD 最大, 即∠PCA 最小, ∵DE=2,DC=4, ∴CE=2 又 EP=ED=2, ∴PC 长的最大值为
8.解析:(1) 考虑到点D纵坐标与点C相同,为3,代入反比例解析式,可得D点坐标为(2,3),根据A、D坐标可得抛物线解析式:
(2) 求t即求P 点位置.
思路1:作外接圆.
作过点B、D的圆且与y轴相切时,切点即为所求P点,考虑到本题只要直接写出结果即可,所以做法只要做对就可.由抛物线解析式可得 B 点坐标为(3, 0),结合 D (2, 3),则BD中点N坐标为
作BD的垂直平分线,即过N点作BD的垂线,
利用 可求得垂直平分线解析式为
三角形 PBD 圆心记为Q, 点Q 在 BD 垂直平分线上, 设Q点坐标为
根据QP=QB, 可得:
解得: (舍)
故Q点坐标为 P点坐标为 所以t的值为
思路2:切割线定理
延长BD交y轴于 M点,当 ·MB 时, ∠BPD 最大.
考虑到B(3,0)、D(2,3),可得直线BD解析式: y=-3x+9,故直线BD与y轴交点 M点坐标为(0, 9),
∴P点坐标为
故t的值为
9解析:(1)由题意得BC=AO=2, BC∥AO, ∴C点坐标为(2, ),设解析式为. 将点 A 坐标代入,解得: ∴抛物线的表达式为
(2)由题意得顶点M坐标为(1,3),令 解得: ∴D点坐标是 (4, 0).
①当点 P线段 EM上时,以PE为斜边在对称轴右侧作等腰直角△PNE,以N为圆心、PN为半径作圆,与MD 相切时,切点即唯一的点Q, 满足∠PQE=45°. ∵△MED是等腰直角三角形,∴点Q为MD中点,∴点Q坐标为( , ),对应P点坐标为(1, ).
②当点 P在M点处时, 过点 E作 EN⊥PD, 则△PEN是等腰直角三角形,以点N为圆心,PN 为半径作圆,过点 D,此时∠PDE=45°, 点 D 即满足条件的点Q, 对应P 点坐标为(1, 3)
③当点P在x轴下方抛物线上时,可得点P坐标为(1,-3).
综上, P 点坐标为(1, ) 或(1, 3) 或(1, - 3).
同课章节目录
