2025年中考数学二轮专题复习 第3章 正方形压轴题讲练 第1节 常见构图 (含解析)
文档属性
| 名称 | 2025年中考数学二轮专题复习 第3章 正方形压轴题讲练 第1节 常见构图 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 230.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 07:30:14 | ||
图片预览




文档简介
第3章 正方形
第1节 常见构图
前言:正方形是最特殊的四边形,边、角、对角线均具有特殊性质,同时,由其自身的轴对称性及中心对称性,使得正方形有更多的考法.
中小学教育资源及组卷应用平台
知识导航
基本性质
四边相等: AB=BC=CD=DA;
四角都是直角: ∠ABC=∠BCD=∠CDA=∠DAB=90°;
对角线: OA=OB=OC=OD, AC⊥BD.
引例1:如图, 点 P 是正方形 ABCD内位于对角线 AC 下方的一点, ∠1=∠2, 则∠BPC 的度数为 °.
解析: ∵∠2+∠BCP=45°, ∠1=∠2,
∴∠1+∠BCP=45°,
∴∠BPC=135°.
引例2:如图,边长为 的正方形ABCD的对角线AC与BD 交于点 O, 将正方形 ABCD沿直线 DF折叠,点 C落在对角线 BD上的点 E处,折痕DF交AC于点M, 则OM=( )
A.
解析: ∵AD=DC= , ∴AC=BD=2, OD= BD=1,
∴选D.
引例3:如图,在正方形纸片ABCD中, E是CD 的中点,将正方形纸片折叠,点B 落在线段 AE 上的点G处, 折痕为AF. 若AD=4, 则 CF的长为 .
解析:∵E点是 CD中点, 由折叠可知AG=AB=4, ∴EG=2 -4,设CF=x,则BF=4-x, FG=4-x,
在Rt△EFG中,
在Rt△CEF中,
解得:
∴CF的长为
双正方形
(1) 与模型相关
手拉手模型: △ABG≌△CBE.
三垂直模型: △FGM≌△MCD.
“8”字型: △AMD∽△EMF.
(2)与对角线相关
若连接BF、BD, 则BF⊥BD.
若连接EG、BD, 则EG∥BD, SAEDG=S△EBG·
引例4:如图, 点C在线段AB上,且AC=2BC, 分别以AC、BC为边在线段AB 的同侧作正方形ACDE、BCFG,连接EC、EG,则tan∠CEG= .
解析:连接CG,则CE⊥CG,∵AC=2BC,∴tan∠CEG=
真 题 演 练
1. 如图, 在正方形ABCD中, E是边AD的中点. 将△ABE 沿直线 BE 翻折, 点 A 落在点 F 处, 连接DF, 那么∠EDF的正切值是 .
2. 如图,在边长为2 的正方形ABCD中,点E、F分别是边AB、BC的中点, 连接EC、FD, 点G、H分别是EC、FD的中点,连接GH,则GH的长度为 .
3. 如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE, 点F是AE的中点, 连接OF交AD于点 G. 若DE=2, OF=3, 则点A到DF的距离为 .
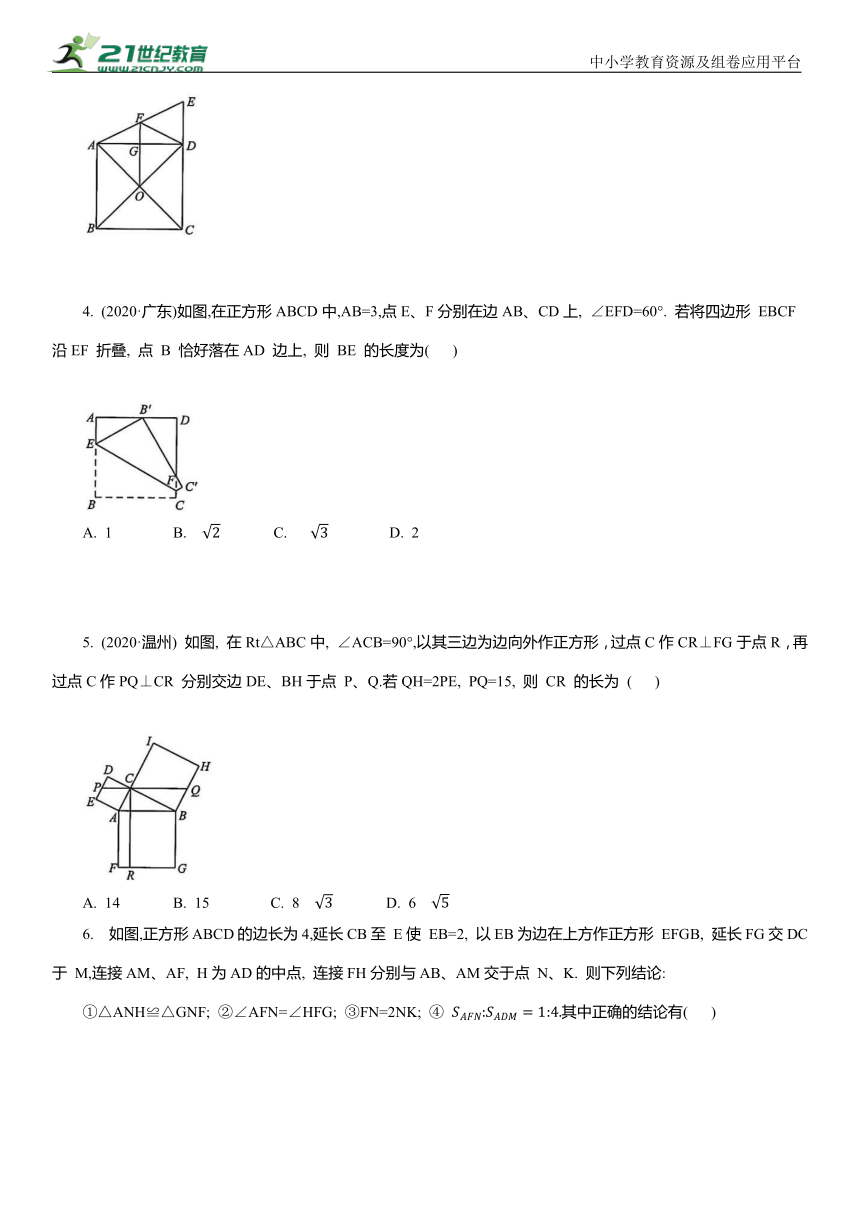
4. (2020·广东)如图,在正方形ABCD中,AB=3,点E、F分别在边AB、CD上, ∠EFD=60°. 若将四边形 EBCF沿EF 折叠, 点 B 恰好落在AD 边上, 则 BE 的长度为( )
A. 1 B. C. D. 2
5. (2020·温州) 如图, 在Rt△ABC中, ∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR 分别交边DE、BH于点 P、Q.若QH=2PE, PQ=15, 则 CR 的长为 ( )
A. 14 B. 15 C. 8 D. 6
6. 如图,正方形ABCD的边长为4,延长CB至 E使 EB=2, 以EB为边在上方作正方形 EFGB, 延长FG交DC于 M,连接AM、AF, H为AD的中点, 连接FH分别与AB、AM交于点 N、K. 则下列结论:
①△ANH≌△GNF; ②∠AFN=∠HFG; ③FN=2NK; ④ 其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
7. 如图, 正方形ABCD和正方形 CGFE的顶点 C、D、E在同一条直线上,顶点B、C、G在同一条直线上. O是EG的中点, ∠EGC的平分线GH过点D, 交BE于点H,连接FH交EG于点M,连接OH. 以下四个结论:①GH⊥BE; ②△EHM∽△FHG; ④ 其中正确的结论是 ( )
A. ①②③ B. ①②④
C. ①③④ D. ②③④
8.如图, 正方形ABCD 的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H. 连接HF、AF, 其中AF交EC于点 M.
(1) 求证: △AHF为等腰直角三角形.
(2) 若AB=3, EC=5, 求EM的长.
9. 如图1,正方形ABDE和BCFG的边AB、BC 在同一条直线上, 且AB=2BC, 取 EF 的中点 M, 连接MD, MG, MB.
(1) 试证明DM⊥MG, 并求 的值.
(2) 如图 2, 将图 1 中的正方形变为菱形, 设∠EAB=2α(0<α<90°), 其它条件不变, 问(1)中 的值有变化吗 若有变化,求出该值(用含α的式子表示);若无变化,说明理由.
1.解析: 如图, 点F如图所示, 连接BF、DF、EF、AF, 记AF与BE交点为H,
由对称可知AF⊥BE,点H是AF中点,又点E是AD中点,∴EH是△DF边所对的中位线, ∴EH∥DF,∴∠EDF=∠AEB, ∴tan∠EDF=tan∠AEB=2.
2解析:勾股定理可得GH=1.
解析:∵DE=2,∴FG=1,∴OG=2,CD=4,∴AD=4,AE=2 由等积法可得点 A 到 DF的距离为 距离为
4. D.
解析: ∵∠EFD=60°, ∴∠B'EF =∠BEF=60°,∴∠AEB'=60°, ∴BE=B'E=2AE, ∴BE=2. 故选 D.A.
5.解析: 连接CE、CH, 易证△CPE∽△CQH, ∴
∴CD=2 , CM=4, AB=10, MR=10, ∴CR=14,∴选A.
6.C.
解析: ∵H是AD中点, 易证△ANH≌△GNF, 故结论①正确;
∵∠HFG=∠AHF, ∠AFN≠∠AHF, ∴∠AFN≠∠HFG, 故结论②错误;
易证点K是HN中点, ∴FN=NH=2NK, 故结论③正确;
考虑到
故结论④正确.
综上, 选C.
7. A.
解析: 易证△BCE≌△DCG, ∴∠BEC=∠DGC,又∠BEC+∠EHD=∠DGC+∠DCG,
∴∠EHD=∠DCG=90°, ∴GH⊥BE. 故结论①正确;
∵∠EHG=∠EFG=90°, ∴E、F、G、H四点共圆,
∴∠HEM=∠GFM, 又EF=GF, ∴∠EHF=∠GHF,
∴△EHM∽△FHG, 故结论②正确;
∵GH平分∠EGB, 且GH⊥BE, ∴△BGE是等腰三角形,
故结论③正确;
易证
故结论④错误.
综上, 选A.
8解析:(1)∵AH∥DG,易证△ABH≌△DCG,∴BH=CG,
∴BC=HG, ∴AB=HG, 易证△ABH≌△HGF, ∴AH=HF,
∵△AHB≌△HFG, ∴∠AHB=∠HFG,
∵∠HFG+∠FHG=90°, ∴∠AHB+∠FHG=90°,
∴∠AHF=90°, ∴△AHF为等腰直角三角形.
(2) 易证△AMD≌△FME, ∴MDE=HD=
∴又
∴EM的长为
解析: (1) 延长GM与DE交于点N,易证△MGF≌△MNE
不妨设正方形 ABDE 边长为2a, 正方形 BCFG的边长为 a,则NE=GF=a, ∴DN=2a-a=a, ∴DN=DG, ∴△DNG为等腰直角三角形, 又M为NG中点, ∴DM⊥MG.
过点 M 作 MH⊥BD 交 BD 于点 H, 则
(2) 连接BF, 易证 BF∥DM, 延长MG与BF交于点 Q,则MQ⊥BF,
易证△MGD≌△QGB, 设MG=m,则
第1节 常见构图
前言:正方形是最特殊的四边形,边、角、对角线均具有特殊性质,同时,由其自身的轴对称性及中心对称性,使得正方形有更多的考法.
中小学教育资源及组卷应用平台
知识导航
基本性质
四边相等: AB=BC=CD=DA;
四角都是直角: ∠ABC=∠BCD=∠CDA=∠DAB=90°;
对角线: OA=OB=OC=OD, AC⊥BD.
引例1:如图, 点 P 是正方形 ABCD内位于对角线 AC 下方的一点, ∠1=∠2, 则∠BPC 的度数为 °.
解析: ∵∠2+∠BCP=45°, ∠1=∠2,
∴∠1+∠BCP=45°,
∴∠BPC=135°.
引例2:如图,边长为 的正方形ABCD的对角线AC与BD 交于点 O, 将正方形 ABCD沿直线 DF折叠,点 C落在对角线 BD上的点 E处,折痕DF交AC于点M, 则OM=( )
A.
解析: ∵AD=DC= , ∴AC=BD=2, OD= BD=1,
∴选D.
引例3:如图,在正方形纸片ABCD中, E是CD 的中点,将正方形纸片折叠,点B 落在线段 AE 上的点G处, 折痕为AF. 若AD=4, 则 CF的长为 .
解析:∵E点是 CD中点, 由折叠可知AG=AB=4, ∴EG=2 -4,设CF=x,则BF=4-x, FG=4-x,
在Rt△EFG中,
在Rt△CEF中,
解得:
∴CF的长为
双正方形
(1) 与模型相关
手拉手模型: △ABG≌△CBE.
三垂直模型: △FGM≌△MCD.
“8”字型: △AMD∽△EMF.
(2)与对角线相关
若连接BF、BD, 则BF⊥BD.
若连接EG、BD, 则EG∥BD, SAEDG=S△EBG·
引例4:如图, 点C在线段AB上,且AC=2BC, 分别以AC、BC为边在线段AB 的同侧作正方形ACDE、BCFG,连接EC、EG,则tan∠CEG= .
解析:连接CG,则CE⊥CG,∵AC=2BC,∴tan∠CEG=
真 题 演 练
1. 如图, 在正方形ABCD中, E是边AD的中点. 将△ABE 沿直线 BE 翻折, 点 A 落在点 F 处, 连接DF, 那么∠EDF的正切值是 .
2. 如图,在边长为2 的正方形ABCD中,点E、F分别是边AB、BC的中点, 连接EC、FD, 点G、H分别是EC、FD的中点,连接GH,则GH的长度为 .
3. 如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE, 点F是AE的中点, 连接OF交AD于点 G. 若DE=2, OF=3, 则点A到DF的距离为 .
4. (2020·广东)如图,在正方形ABCD中,AB=3,点E、F分别在边AB、CD上, ∠EFD=60°. 若将四边形 EBCF沿EF 折叠, 点 B 恰好落在AD 边上, 则 BE 的长度为( )
A. 1 B. C. D. 2
5. (2020·温州) 如图, 在Rt△ABC中, ∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR 分别交边DE、BH于点 P、Q.若QH=2PE, PQ=15, 则 CR 的长为 ( )
A. 14 B. 15 C. 8 D. 6
6. 如图,正方形ABCD的边长为4,延长CB至 E使 EB=2, 以EB为边在上方作正方形 EFGB, 延长FG交DC于 M,连接AM、AF, H为AD的中点, 连接FH分别与AB、AM交于点 N、K. 则下列结论:
①△ANH≌△GNF; ②∠AFN=∠HFG; ③FN=2NK; ④ 其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
7. 如图, 正方形ABCD和正方形 CGFE的顶点 C、D、E在同一条直线上,顶点B、C、G在同一条直线上. O是EG的中点, ∠EGC的平分线GH过点D, 交BE于点H,连接FH交EG于点M,连接OH. 以下四个结论:①GH⊥BE; ②△EHM∽△FHG; ④ 其中正确的结论是 ( )
A. ①②③ B. ①②④
C. ①③④ D. ②③④
8.如图, 正方形ABCD 的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H. 连接HF、AF, 其中AF交EC于点 M.
(1) 求证: △AHF为等腰直角三角形.
(2) 若AB=3, EC=5, 求EM的长.
9. 如图1,正方形ABDE和BCFG的边AB、BC 在同一条直线上, 且AB=2BC, 取 EF 的中点 M, 连接MD, MG, MB.
(1) 试证明DM⊥MG, 并求 的值.
(2) 如图 2, 将图 1 中的正方形变为菱形, 设∠EAB=2α(0<α<90°), 其它条件不变, 问(1)中 的值有变化吗 若有变化,求出该值(用含α的式子表示);若无变化,说明理由.
1.解析: 如图, 点F如图所示, 连接BF、DF、EF、AF, 记AF与BE交点为H,
由对称可知AF⊥BE,点H是AF中点,又点E是AD中点,∴EH是△DF边所对的中位线, ∴EH∥DF,∴∠EDF=∠AEB, ∴tan∠EDF=tan∠AEB=2.
2解析:勾股定理可得GH=1.
解析:∵DE=2,∴FG=1,∴OG=2,CD=4,∴AD=4,AE=2 由等积法可得点 A 到 DF的距离为 距离为
4. D.
解析: ∵∠EFD=60°, ∴∠B'EF =∠BEF=60°,∴∠AEB'=60°, ∴BE=B'E=2AE, ∴BE=2. 故选 D.A.
5.解析: 连接CE、CH, 易证△CPE∽△CQH, ∴
∴CD=2 , CM=4, AB=10, MR=10, ∴CR=14,∴选A.
6.C.
解析: ∵H是AD中点, 易证△ANH≌△GNF, 故结论①正确;
∵∠HFG=∠AHF, ∠AFN≠∠AHF, ∴∠AFN≠∠HFG, 故结论②错误;
易证点K是HN中点, ∴FN=NH=2NK, 故结论③正确;
考虑到
故结论④正确.
综上, 选C.
7. A.
解析: 易证△BCE≌△DCG, ∴∠BEC=∠DGC,又∠BEC+∠EHD=∠DGC+∠DCG,
∴∠EHD=∠DCG=90°, ∴GH⊥BE. 故结论①正确;
∵∠EHG=∠EFG=90°, ∴E、F、G、H四点共圆,
∴∠HEM=∠GFM, 又EF=GF, ∴∠EHF=∠GHF,
∴△EHM∽△FHG, 故结论②正确;
∵GH平分∠EGB, 且GH⊥BE, ∴△BGE是等腰三角形,
故结论③正确;
易证
故结论④错误.
综上, 选A.
8解析:(1)∵AH∥DG,易证△ABH≌△DCG,∴BH=CG,
∴BC=HG, ∴AB=HG, 易证△ABH≌△HGF, ∴AH=HF,
∵△AHB≌△HFG, ∴∠AHB=∠HFG,
∵∠HFG+∠FHG=90°, ∴∠AHB+∠FHG=90°,
∴∠AHF=90°, ∴△AHF为等腰直角三角形.
(2) 易证△AMD≌△FME, ∴MDE=HD=
∴又
∴EM的长为
解析: (1) 延长GM与DE交于点N,易证△MGF≌△MNE
不妨设正方形 ABDE 边长为2a, 正方形 BCFG的边长为 a,则NE=GF=a, ∴DN=2a-a=a, ∴DN=DG, ∴△DNG为等腰直角三角形, 又M为NG中点, ∴DM⊥MG.
过点 M 作 MH⊥BD 交 BD 于点 H, 则
(2) 连接BF, 易证 BF∥DM, 延长MG与BF交于点 Q,则MQ⊥BF,
易证△MGD≌△QGB, 设MG=m,则
同课章节目录
