2025年中考数学二轮专题复习 第4章 圆 压轴题讲练第1节 切线的判定 (含解析)
文档属性
| 名称 | 2025年中考数学二轮专题复习 第4章 圆 压轴题讲练第1节 切线的判定 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 264.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 07:29:53 | ||
图片预览



文档简介
第4章 圆
第1节 切线的判定
前言:“切线的判定”是圆综合题常见问题之一,从性质出发,探讨出判定的方法,对大量中考题解法的提炼总结,可发现常见的证明切线的构图及方法.
知 识 导 航
1 性质与判定
(1)性质:切线垂直于过切点的半径.(连半径,得垂直)
引例1:如图, 在△ABC中, ∠C=90°,AC=3, BC=4, 则△ABC的内切圆半径r= .
解析: ∴内切圆半径r=1.
(2) 切线的判定:
判定1(定义法):和圆只有一个交点的直线是圆的切线;判定 2 (距离法):到圆心距离等于半径的直线是圆的切线;(常用于已知数据的计算,比如动圆相切问题.)
判定3(判定定理):经过半径外端且垂直于这条半径的直线是圆的切线.
有交点:连半径,证垂直
即.无交点:作垂直,证半径 多用于几何证明.
多数情况为有交点,重点考虑如何证垂直:
① 证明和已知垂线平行; ②证明夹角为直角.
引例2:如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径作圆,与BC相切于点 C,过点A作AD⊥BO交BO的延长线于点 D, 且∠AOD=∠BAD.
(1) 求证: AB为⊙O的切线;
(2) 若BC=6, tan∠ABC= 求AD的长.
解析: (1) ∵∠AOD+∠DAO=90°, ∠ABD+∠BAD=90°,且∠AOD=∠BAD,
∴∠DAO=∠ABD, 又∠DAO=∠OBC,
∴∠ABD=∠OBC,
过点O作OH⊥AB交AB于H点, 则OH=OC,
∴△BOH≌△BOC,
∴OH=OC,
中小学教育资源及组卷应用平台
∴AB 是⊙O的切线.
BH=BC=6, AH=4, OH=3, OA=5,
∴AD的长为2
常见相切图
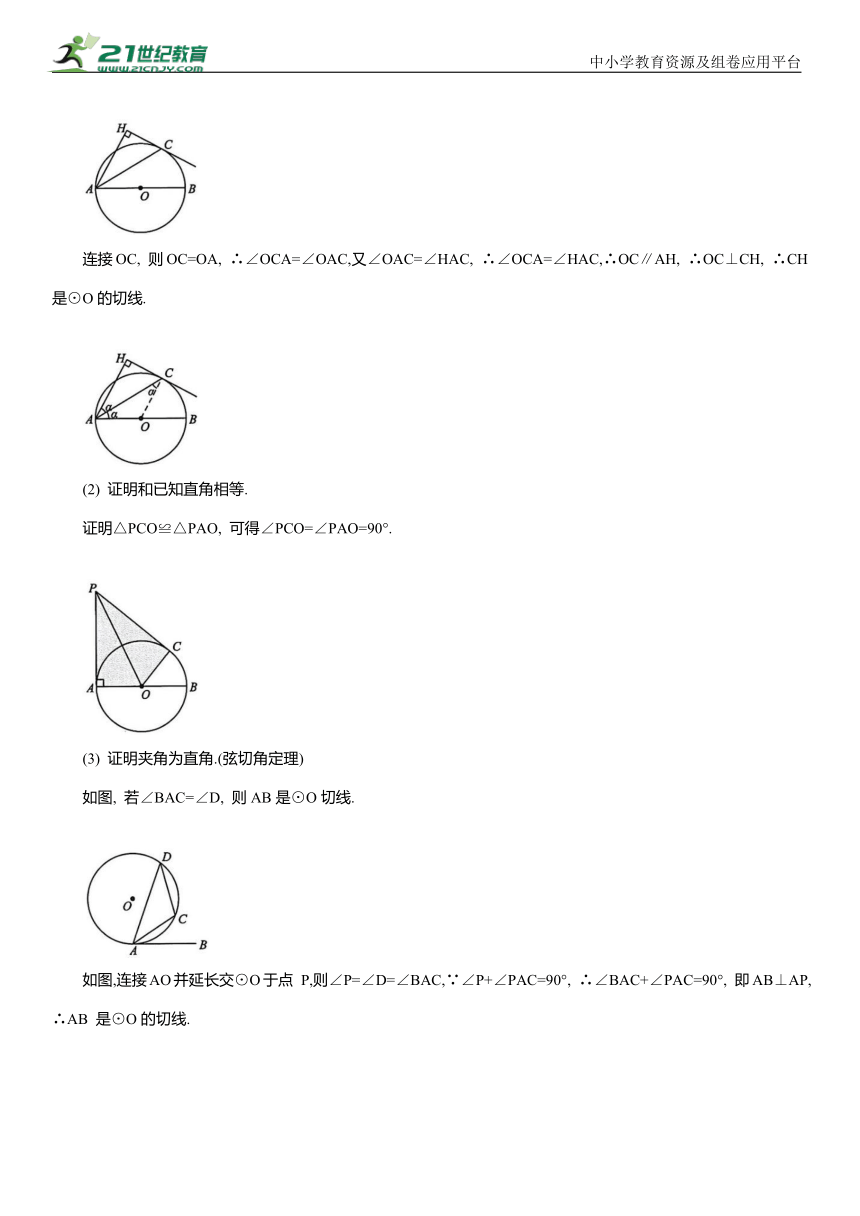
(1) 角分+等腰得平行:
点C在以AB为直径的⊙O上, AH⊥CH, 且AC平分∠HAB.
连接OC, 则OC=OA, ∴∠OCA=∠OAC,又∠OAC=∠HAC, ∴∠OCA=∠HAC,∴OC∥AH, ∴OC⊥CH, ∴CH是⊙O的切线.
(2) 证明和已知直角相等.
证明△PCO≌△PAO, 可得∠PCO=∠PAO=90°.
(3) 证明夹角为直角.(弦切角定理)
如图, 若∠BAC=∠D, 则AB是⊙O切线.
如图,连接AO并延长交⊙O于点 P,则∠P=∠D=∠BAC,∵∠P+∠PAC=90°, ∴∠BAC+∠PAC=90°, 即AB⊥AP,∴AB 是⊙O的切线.
真题演练
1. 如图, AB为⊙O的直径, C为⊙O上一点, ∠ABC的平分线交⊙O于点D, DE⊥BC于点E.
(1) 试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F, 若BE=3 , DF=3,求图中阴影部分的面积.
2. 如图,AB为⊙O的直径,点C在⊙O上,AD⊥CD于点D, 且AC平分∠DAB,
求证:(1) 直线DC是⊙O的切线;
3. 如图, 在△ABC中, ∠C=90°, AE平分∠BAC交BC于点E, O是AB上一点, 经过A、E两点的⊙O交AB于点D, 连接DE, 作∠DEA的平分线EF交⊙O于点F, 连接AF.
(1) 求证: BC是⊙O的切线.
(2)若 求线段AC的长.
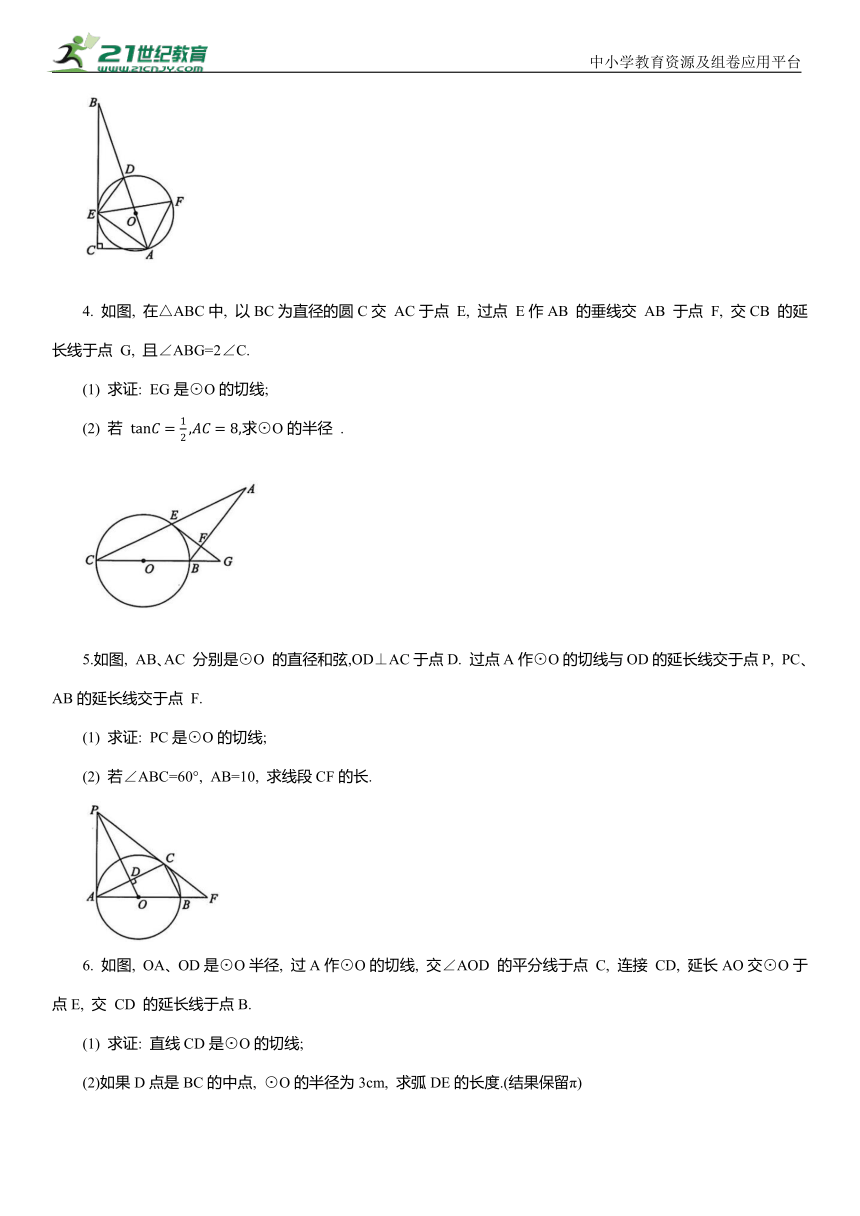
4. 如图, 在△ABC中, 以BC为直径的圆C交 AC于点 E, 过点 E作AB 的垂线交 AB 于点 F, 交CB 的延长线于点 G, 且∠ABG=2∠C.
(1) 求证: EG是⊙O的切线;
(2) 若 求⊙O的半径 .
5.如图, AB、AC 分别是⊙O 的直径和弦,OD⊥AC于点D. 过点A作⊙O的切线与OD的延长线交于点P, PC、AB的延长线交于点 F.
(1) 求证: PC是⊙O的切线;
(2) 若∠ABC=60°, AB=10, 求线段CF的长.
6. 如图, OA、OD是⊙O半径, 过A作⊙O的切线, 交∠AOD 的平分线于点 C, 连接 CD, 延长AO交⊙O于点E, 交 CD 的延长线于点B.
(1) 求证: 直线CD是⊙O的切线;
(2)如果D点是BC的中点, ⊙O的半径为3cm, 求弧DE的长度.(结果保留π)
7. 如图,直线AD经过⊙O上的点A,△ABC为⊙O的内接三角形, 并且∠CAD=∠B.
(1) 判断直线AD与⊙O的位置关系,并说明理由;
(2) 若∠CAD=30°, ⊙O 的半径为1, 求图中阴影部分的面积.(结果保留π)
8.如图, 在Rt△ABC中, ∠ACB=90°,CD是斜边B上的中线,以CD为直径的⊙O分别交AC、BC于点 M、N, 过点N作 NE⊥AB, 垂足为E.
(1) 若⊙O的半径为 , AC=6, 求BN的长;
(2) 求证: NE与⊙O相切.
9. 如图,在 Rt△ABC中, ∠C=90°, 点O、D分别为AB、BC的中点,连接OD,作⊙O与AC相切于点E, 在AC边上取一点F, 使DF=DO, 连接DF.
(1) 判断直线DF与⊙O的位置关系,并说明理由;
(2)当. 时,求⊙O的半径.
10. 如图,⊙O是△ABC的外接圆,AC是直径, 弦BD=BA, EB⊥DC, 交 DC的延长线于点 E.
(1) 求证: BE是⊙O的切线;
(2)当 时, 求AD的长.
第1节 切线的判定
解析: (1) 相切.
连接OD, ∵BD平分∠ABE, ∴∠ABD=∠EBD,
∵OB=OD, ∴∠OBD=∠ODB,
∴∠EBD=∠ODB, ∴OD∥BE,
∵DE⊥BE, ∴OD⊥DE,
∴DE与圆O相切.
(2) 易证△BED≌△BFD, ∴BF=BE=3 , 又DF=3,∴∠ABD=30°, 连接 OD, 则∠AOD=60°, 易证(
故阴影部分面积为
2.解析: (1) 连接OC, ∵OA=OC, ∴∠OAC=∠OCA,又AC平分∠DAB, ∴∠DAC=∠OAC,
∴∠OCA=∠DAC, ∴AD∥OC,
∵AD⊥CD, ∴OC⊥CD,
∴DC是圆O的切线.
(2) 连接BC, 过点 C作 CH⊥AN交AB于H点,则AC =AH·AB, ∵AH=AD, AB=2AO,
3. 解析: (1) 连接EO, 则OA=OE, ∴∠OAE=∠OEA,又AE平分∠BAC, ∴∠OAE=∠CAE, ∴∠OEA=∠CAE,∴OE∥AC, ∵AC⊥BC, ∴OE⊥BC,
∴BC是圆O的切线.
(2) EF平分∠AED, 则点F是半圆AD中点, 连接OF,则△AOF 是等腰直角三角形,. ∵AE平分∠BAC,∴cos∠CAE=cos∠EAD= 即 故AC的长为
解析: (1) 连接OE, 则OE=OC, ∴∠OEC=∠OCE,∴∠EOG=2∠C, 又∠ABG=2∠C, ∴∠EOG=∠ABG,∴OE∥AB, ∵EG⊥AB, ∴EG⊥OE,
∴EG是圆O的切线.
(2)连接BE,则BE⊥AC,∵OE∥AB, ∴△ABC是等腰三角形, ∴E是AC中点, 故圆O的半径为
解析:(1) 连接OC, ∵OP⊥AC, ∴OP平分AC,∴OP 是AC的垂直平分线, ∴PA=PC,
易证△POA≌△POC, ∴∠PCO=∠PAO=90°, ∴OC⊥PC,∴PC是圆O的切线.
(2)若∠ABC=60°则△OBC是等边三角形,∴∠BOC=60°,OC=OB=5, 在Rt△OCF中, 故CF的长为5
6. 解析: (1) 由题意可证△COA≌△COD,∴∠ODC=∠OAC=90°, 即OD⊥CD,∴CD 是圆O的切线.
(2) 若点D是BC的中点, 则△BOC是等腰三角形,∴∠OBC=∠OCB, 又∠OCB=∠OCA,
∴设∠OBC=∠OCB=∠OCA=α,
∴3α=90°, α=30°, ∴∠BOD=60°,
∴弧
故弧DE 的长度是πcm.
解析: (1) 相切.
连接AO并延长交圆O于点 P, 连接CP, 则∠P=∠B,又∵∠B=∠CAD, ∴∠P=∠CAD,
∵∠P+∠PAC=90°, ∴∠CAD+∠PAC=90°,
∴PA⊥AD, ∴AD是圆O的切线.
(2) 连接OC, 则∠AOC=2∠APC=2∠CAD=60°, 故阴影部分的面积为
8. 解析:(1) ∵r= , ∴CD=5, ∴AB=10, ∴BC=8,连接DN, 则DN⊥BC, ∴DN∥AC, ∴点N是BC中点,
故BN的长为4.
(2) 连接NO,
∵N、O分别是BC、CD中点, ∴NO∥BD,
∵NE⊥BD, ∴NE⊥NO,
∴NE 与圆O相切.
解析: (1) 相切.
连接OE, 则OE⊥AC, ∴点E是AC边中点,连接OF, 过点O作OH⊥DF交DF于H点,
∵DO∥AC, ∴∠DOF=∠OFA,
又DO=DF, ∴∠DOF=∠DFO, ∴∠OFA=∠OFD,易证△OFE≌△OFH, ∴OH=OE,
∴DF是圆O的切线.
(2) 设半径为r, 则CD=r, DF=DO= r, ∴CF= r,又CF= , ∴r=1,
10. 解析:(1)连接BO并延长, 分别交AD、圆O于点 H、Q, 易证△BDQ≌△BAQ, ∴DQ=AQ, 又AB=DB,
∴BQ是AD的垂直平分线, ∴BQ⊥AD,
∵AC是直径, ∴∠ADC=90°, 又∠E=90°, ∴AD∥BE,
∴BQ⊥BE, ∴BE是圆O的切线.
(2) ∵∠BAC=∠CBE, ∴∠ACB=∠BCE,
故AD的长为
第1节 切线的判定
前言:“切线的判定”是圆综合题常见问题之一,从性质出发,探讨出判定的方法,对大量中考题解法的提炼总结,可发现常见的证明切线的构图及方法.
知 识 导 航
1 性质与判定
(1)性质:切线垂直于过切点的半径.(连半径,得垂直)
引例1:如图, 在△ABC中, ∠C=90°,AC=3, BC=4, 则△ABC的内切圆半径r= .
解析: ∴内切圆半径r=1.
(2) 切线的判定:
判定1(定义法):和圆只有一个交点的直线是圆的切线;判定 2 (距离法):到圆心距离等于半径的直线是圆的切线;(常用于已知数据的计算,比如动圆相切问题.)
判定3(判定定理):经过半径外端且垂直于这条半径的直线是圆的切线.
有交点:连半径,证垂直
即.无交点:作垂直,证半径 多用于几何证明.
多数情况为有交点,重点考虑如何证垂直:
① 证明和已知垂线平行; ②证明夹角为直角.
引例2:如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径作圆,与BC相切于点 C,过点A作AD⊥BO交BO的延长线于点 D, 且∠AOD=∠BAD.
(1) 求证: AB为⊙O的切线;
(2) 若BC=6, tan∠ABC= 求AD的长.
解析: (1) ∵∠AOD+∠DAO=90°, ∠ABD+∠BAD=90°,且∠AOD=∠BAD,
∴∠DAO=∠ABD, 又∠DAO=∠OBC,
∴∠ABD=∠OBC,
过点O作OH⊥AB交AB于H点, 则OH=OC,
∴△BOH≌△BOC,
∴OH=OC,
中小学教育资源及组卷应用平台
∴AB 是⊙O的切线.
BH=BC=6, AH=4, OH=3, OA=5,
∴AD的长为2
常见相切图
(1) 角分+等腰得平行:
点C在以AB为直径的⊙O上, AH⊥CH, 且AC平分∠HAB.
连接OC, 则OC=OA, ∴∠OCA=∠OAC,又∠OAC=∠HAC, ∴∠OCA=∠HAC,∴OC∥AH, ∴OC⊥CH, ∴CH是⊙O的切线.
(2) 证明和已知直角相等.
证明△PCO≌△PAO, 可得∠PCO=∠PAO=90°.
(3) 证明夹角为直角.(弦切角定理)
如图, 若∠BAC=∠D, 则AB是⊙O切线.
如图,连接AO并延长交⊙O于点 P,则∠P=∠D=∠BAC,∵∠P+∠PAC=90°, ∴∠BAC+∠PAC=90°, 即AB⊥AP,∴AB 是⊙O的切线.
真题演练
1. 如图, AB为⊙O的直径, C为⊙O上一点, ∠ABC的平分线交⊙O于点D, DE⊥BC于点E.
(1) 试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F, 若BE=3 , DF=3,求图中阴影部分的面积.
2. 如图,AB为⊙O的直径,点C在⊙O上,AD⊥CD于点D, 且AC平分∠DAB,
求证:(1) 直线DC是⊙O的切线;
3. 如图, 在△ABC中, ∠C=90°, AE平分∠BAC交BC于点E, O是AB上一点, 经过A、E两点的⊙O交AB于点D, 连接DE, 作∠DEA的平分线EF交⊙O于点F, 连接AF.
(1) 求证: BC是⊙O的切线.
(2)若 求线段AC的长.
4. 如图, 在△ABC中, 以BC为直径的圆C交 AC于点 E, 过点 E作AB 的垂线交 AB 于点 F, 交CB 的延长线于点 G, 且∠ABG=2∠C.
(1) 求证: EG是⊙O的切线;
(2) 若 求⊙O的半径 .
5.如图, AB、AC 分别是⊙O 的直径和弦,OD⊥AC于点D. 过点A作⊙O的切线与OD的延长线交于点P, PC、AB的延长线交于点 F.
(1) 求证: PC是⊙O的切线;
(2) 若∠ABC=60°, AB=10, 求线段CF的长.
6. 如图, OA、OD是⊙O半径, 过A作⊙O的切线, 交∠AOD 的平分线于点 C, 连接 CD, 延长AO交⊙O于点E, 交 CD 的延长线于点B.
(1) 求证: 直线CD是⊙O的切线;
(2)如果D点是BC的中点, ⊙O的半径为3cm, 求弧DE的长度.(结果保留π)
7. 如图,直线AD经过⊙O上的点A,△ABC为⊙O的内接三角形, 并且∠CAD=∠B.
(1) 判断直线AD与⊙O的位置关系,并说明理由;
(2) 若∠CAD=30°, ⊙O 的半径为1, 求图中阴影部分的面积.(结果保留π)
8.如图, 在Rt△ABC中, ∠ACB=90°,CD是斜边B上的中线,以CD为直径的⊙O分别交AC、BC于点 M、N, 过点N作 NE⊥AB, 垂足为E.
(1) 若⊙O的半径为 , AC=6, 求BN的长;
(2) 求证: NE与⊙O相切.
9. 如图,在 Rt△ABC中, ∠C=90°, 点O、D分别为AB、BC的中点,连接OD,作⊙O与AC相切于点E, 在AC边上取一点F, 使DF=DO, 连接DF.
(1) 判断直线DF与⊙O的位置关系,并说明理由;
(2)当. 时,求⊙O的半径.
10. 如图,⊙O是△ABC的外接圆,AC是直径, 弦BD=BA, EB⊥DC, 交 DC的延长线于点 E.
(1) 求证: BE是⊙O的切线;
(2)当 时, 求AD的长.
第1节 切线的判定
解析: (1) 相切.
连接OD, ∵BD平分∠ABE, ∴∠ABD=∠EBD,
∵OB=OD, ∴∠OBD=∠ODB,
∴∠EBD=∠ODB, ∴OD∥BE,
∵DE⊥BE, ∴OD⊥DE,
∴DE与圆O相切.
(2) 易证△BED≌△BFD, ∴BF=BE=3 , 又DF=3,∴∠ABD=30°, 连接 OD, 则∠AOD=60°, 易证(
故阴影部分面积为
2.解析: (1) 连接OC, ∵OA=OC, ∴∠OAC=∠OCA,又AC平分∠DAB, ∴∠DAC=∠OAC,
∴∠OCA=∠DAC, ∴AD∥OC,
∵AD⊥CD, ∴OC⊥CD,
∴DC是圆O的切线.
(2) 连接BC, 过点 C作 CH⊥AN交AB于H点,则AC =AH·AB, ∵AH=AD, AB=2AO,
3. 解析: (1) 连接EO, 则OA=OE, ∴∠OAE=∠OEA,又AE平分∠BAC, ∴∠OAE=∠CAE, ∴∠OEA=∠CAE,∴OE∥AC, ∵AC⊥BC, ∴OE⊥BC,
∴BC是圆O的切线.
(2) EF平分∠AED, 则点F是半圆AD中点, 连接OF,则△AOF 是等腰直角三角形,. ∵AE平分∠BAC,∴cos∠CAE=cos∠EAD= 即 故AC的长为
解析: (1) 连接OE, 则OE=OC, ∴∠OEC=∠OCE,∴∠EOG=2∠C, 又∠ABG=2∠C, ∴∠EOG=∠ABG,∴OE∥AB, ∵EG⊥AB, ∴EG⊥OE,
∴EG是圆O的切线.
(2)连接BE,则BE⊥AC,∵OE∥AB, ∴△ABC是等腰三角形, ∴E是AC中点, 故圆O的半径为
解析:(1) 连接OC, ∵OP⊥AC, ∴OP平分AC,∴OP 是AC的垂直平分线, ∴PA=PC,
易证△POA≌△POC, ∴∠PCO=∠PAO=90°, ∴OC⊥PC,∴PC是圆O的切线.
(2)若∠ABC=60°则△OBC是等边三角形,∴∠BOC=60°,OC=OB=5, 在Rt△OCF中, 故CF的长为5
6. 解析: (1) 由题意可证△COA≌△COD,∴∠ODC=∠OAC=90°, 即OD⊥CD,∴CD 是圆O的切线.
(2) 若点D是BC的中点, 则△BOC是等腰三角形,∴∠OBC=∠OCB, 又∠OCB=∠OCA,
∴设∠OBC=∠OCB=∠OCA=α,
∴3α=90°, α=30°, ∴∠BOD=60°,
∴弧
故弧DE 的长度是πcm.
解析: (1) 相切.
连接AO并延长交圆O于点 P, 连接CP, 则∠P=∠B,又∵∠B=∠CAD, ∴∠P=∠CAD,
∵∠P+∠PAC=90°, ∴∠CAD+∠PAC=90°,
∴PA⊥AD, ∴AD是圆O的切线.
(2) 连接OC, 则∠AOC=2∠APC=2∠CAD=60°, 故阴影部分的面积为
8. 解析:(1) ∵r= , ∴CD=5, ∴AB=10, ∴BC=8,连接DN, 则DN⊥BC, ∴DN∥AC, ∴点N是BC中点,
故BN的长为4.
(2) 连接NO,
∵N、O分别是BC、CD中点, ∴NO∥BD,
∵NE⊥BD, ∴NE⊥NO,
∴NE 与圆O相切.
解析: (1) 相切.
连接OE, 则OE⊥AC, ∴点E是AC边中点,连接OF, 过点O作OH⊥DF交DF于H点,
∵DO∥AC, ∴∠DOF=∠OFA,
又DO=DF, ∴∠DOF=∠DFO, ∴∠OFA=∠OFD,易证△OFE≌△OFH, ∴OH=OE,
∴DF是圆O的切线.
(2) 设半径为r, 则CD=r, DF=DO= r, ∴CF= r,又CF= , ∴r=1,
10. 解析:(1)连接BO并延长, 分别交AD、圆O于点 H、Q, 易证△BDQ≌△BAQ, ∴DQ=AQ, 又AB=DB,
∴BQ是AD的垂直平分线, ∴BQ⊥AD,
∵AC是直径, ∴∠ADC=90°, 又∠E=90°, ∴AD∥BE,
∴BQ⊥BE, ∴BE是圆O的切线.
(2) ∵∠BAC=∠CBE, ∴∠ACB=∠BCE,
故AD的长为
同课章节目录
