2025年中考数学二轮专题复习 第3章 正方形压轴题讲练第3节 当半角遇上三垂直 (含解析)
文档属性
| 名称 | 2025年中考数学二轮专题复习 第3章 正方形压轴题讲练第3节 当半角遇上三垂直 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 207.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 07:29:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第3节 当半角遇上三垂直
前言:在第2章中的半角模型和三垂直模型都有正方形的身影,把这两个模型结合起来,问题将变得更有趣.
知 识 导 航
1 模型回顾
(1) 三垂直模型
(2) 半角模型
引例1:如图,四边形ACDF 是正方形,∠CEA和∠ABF都是直角且点 E、A、B三点共线, AB=4, 则阴影部分的面积是 .
解析: 由题意得△CEA≌△ABF, ∴CE=AB=4,
当半角遇上三垂直
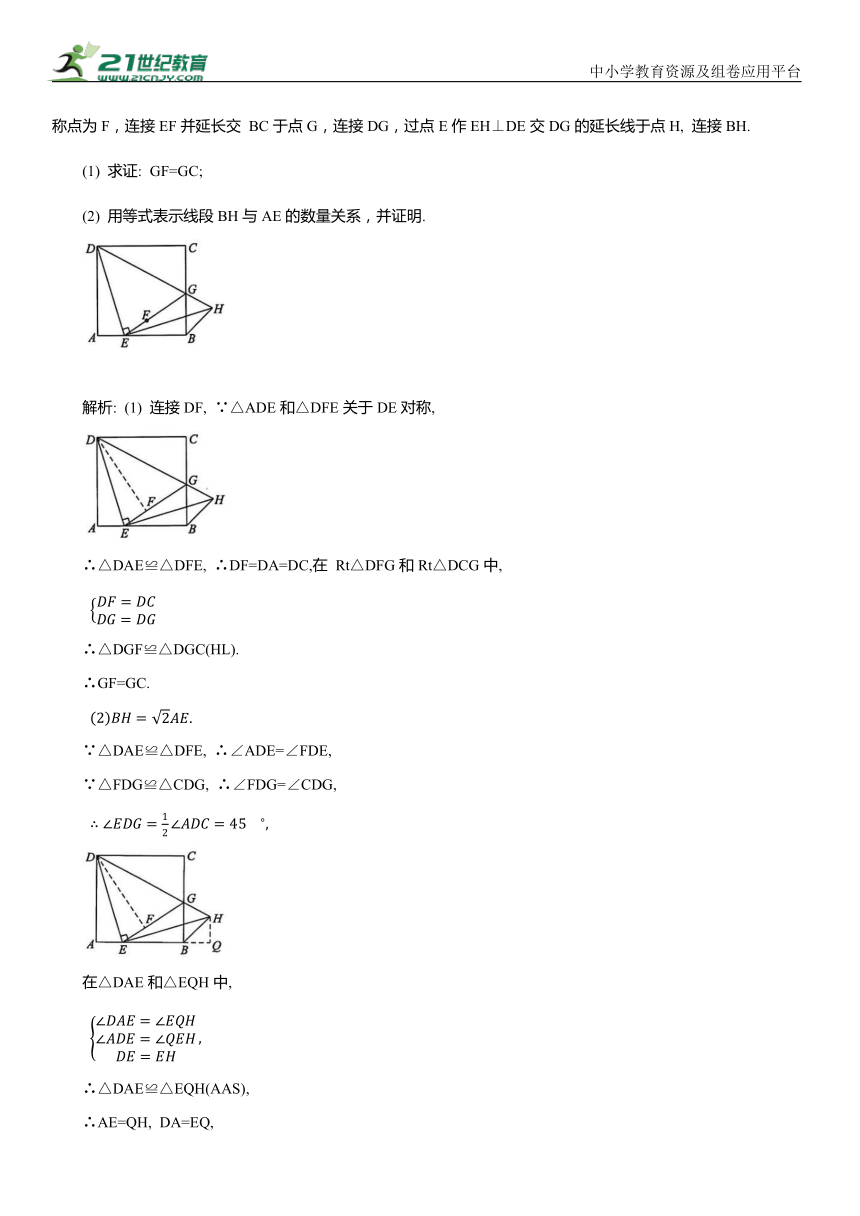
引例2:如图,在正方形ABCD中, E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交 BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H, 连接BH.
(1) 求证: GF=GC;
(2) 用等式表示线段BH与AE的数量关系,并证明.
解析: (1) 连接DF, ∵△ADE和△DFE关于DE对称,
∴△DAE≌△DFE, ∴DF=DA=DC,在 Rt△DFG和Rt△DCG中,
∴△DGF≌△DGC(HL).
∴GF=GC.
∵△DAE≌△DFE, ∴∠ADE=∠FDE,
∵△FDG≌△CDG, ∴∠FDG=∠CDG,
在△DAE和△EQH中,
∴△DAE≌△EQH(AAS),
∴AE=QH, DA=EQ,
又∵AB=DA=EQ, ∴AE=BQ,
∴BQ=HQ, ∴△BQH是等腰直角三角形,
模型总结
本题巧妙地将半角与三垂直结合在一张图中,条件与结论的巧妙组合,还可以有更多变形.
在引例2的图中,除了正方形条件外,其实还存在另外三个条件与结论:
(1)∠DEH=90°;(2)∠EDH=45°;(3)∠CBH=45°.
其中任意两个组合均可得到第三个,引例2是由(1)、(2) 结合得到(3).
变式1: 由 (1)、(3) → (2)
如图,在正方形ABCD中,E是AB边上一点,过点E作EH⊥DE, 连接BH, ∠CBH=45°, 求证: ∠EDH=45°.
解析:可以采用构造三垂直思路,但是对于△DAE和△EQH,并没有已知的相等线段,此路不通.
不同的条件下方法会不同,恰当地利用题目的已知条件,是解题的关键. 比如∠CBH=45°如何运用
证明: 在AD边上取点F使得AF=AE, 连接EF,
∴∠DFE=135°=∠EBH,
由题意可得: ∠FDE=∠BEH, DF=EB,
∴△DFE≌△EBH, ∴DE=DH,
∴△DEH是等腰直角三角形, ∴∠DEH=45°.
变式2: 由(2)、(3)→ (1)
如图,在正方形ABCD中,E是AB边上一点,∠EDH=∠CBH=45°, 求证: DE⊥EH.
证明: ∵∠EDH=45°, ∠EBH=90°+45°=135°,∴∠EDH+∠EBH=180°, ∴B、E、D、H四点共圆,连接BD, ∴∠DEH=∠DBH=90°,∴DE⊥EH.
引例3:如图, 在正方形ABCD中, E是DC边上一点,(与D、C不重合), 连接AE, 将△ADE沿AE所在的直线折叠得到△AFE, 延长EF交BC于 G, 连接AG,作 GH⊥AG, 与AE的延长线交于点 H, 连接CH. 显然 AE是∠DAF的平分线, EA是∠DEF的平分线. 仔细观察, 请逐一找出图中其他的角平分线(仅限于小于 180°的角平分线),并说明理由.
解析: (1) AG平分∠BAF;
(2) AG平分∠BGF;
(3) GH平分∠EGM;
(4) CH平分∠DCM.
以下证明:
(1) 由题意得: △AFG≌△ABG, ∴AG平分∠BAF;
(2) 同理, AG平分∠BGF;
(3)过点H作HN⊥BM,易证:△ABG≌△GNH,∴HN=BG,GN=AB, ∴BG=CN, ∴CN=HN, ∴△CNH是等腰直角三角形, ∴∠HCN=45°, ∴CH平分∠DCN;
(4) ∵∠AGH=90°, AG平分∠BGE,∴可证GH平分∠EGM.
真 题 演 练
1. 如图,在矩形ABCD中, AD=4, 点E在边 AD 上, 连接 CE, 以CE为边向右上方作正方形 CEFG,作FH⊥AD, 垂足为H, 连接AF.
(1) 求证: FH=ED;
(2) 当AE为何值时, △AEF的面积最大
2. 如图, 线段AB=8, 射线 BG⊥AB, P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F (点F与点A、B不重合).
(1) 求证: △AEP≌△CEP;
(2) 判断CF与AB 的位置关系,并说明理由;
(3) 求△AEF的周长.
3. 如图,在正方形ABCD中, 点E是AB边上一点, 以DE为边作正方形 DEFG, DF与BC交于点 M,延长EM交GF于点H, EF与CB交于点N, 连接CG.
(1) 求证: CD⊥CG;
(2) 若 求 的值;
(3) 已知正方形 ABCD 的边长为1, 点 E 在运动过程中,EM的长能否为 请说明理由.
4. 如图, 已知边长为10 的正方形ABCD,E是BC边上一动点(与B、C不重合), 连结AE, G是BC延长线上的点,过点 E作AE的垂线交. 的角平分线于点F, 若
(1)求证:
(2)若 求 的面积;
(3) 请直接写出EC为何值时, 的面积最大.
5. 如图, 正方形ABCD的边长为4, 点E在边AB上, BE=1, ∠DAM=45°, 点F在射线AM上,且 过点 F 作 AD 的平行线交 BA 的延长线于点 H,CF与AD 相交于点 G, 连接EC、EG、EF. 下列结论:
①△ECF的面积为
②△AEG的周长为8;
其中正确的是( )
A. ①②③ B. ①③
C. ①② D. ②③
6. 如图, 正方形ABCD的边长为a, 点E在边 AB 上运动(不与点A、B 重合), ∠DAM=45°, 点F在射线AM 上, 且 CF与AD 相交于点 G, 连接EC、EF、EG, 则下列结论:
①∠ECF=45°;
②△AEG的周长为
④△EAF的面积的最大值
其中正确的结论是 .(填写所有正确结论的序号)
第3节 当半角遇上三垂直
1. 解析: (1) 易证△EHF≌△CDE, ∴FH=ED.
(2) 设AE=x, 则DE=4-x, FH=DE=4-x,
当x=2时, S. AEF 取到最大值2,故当AE=2时, △AEF的面积最大.
2. 解析: (1) 在△AEP和△CEP中,
∴△APE≌△CEP (SAS).
(2) ∵△PAE≌△PCE, ∴∠PAE=∠PCE,又∠EAP=∠BAP, ∴∠PCE=∠BAP,
∵∠PCE+∠CPA=∠BAP+∠AFC, ∴∠AFC=∠CPA=90°,
∴CH⊥AB.
(3) CAAEF=AE+AF+EF=CE+EF+AF=CF+AF,过点C作CH⊥BG交BG于点H, 过点P作 PN⊥CF交CF.于点 N,
易证△ABP≌△PHC, ∴PH=AB=8, ∴CN=PH=8,又NF=PB=CH=BF, ∴AF+FN=AF+FB=AB=8,∴C△AEP=CF+AF=CN+NF=PH+AB=16,∴△AEF的周长为16.
3. 解析:(1)易证△DAE≌△DCG,∴∠DCG=∠DAE=90°,∴CD⊥CG.
(2) 易证∠MEN=∠MGF=∠CDG=∠ADE,易证△FME≌△FMG, ∴ME=MG, ∠FEM=∠FGM,
∴△EMN≌△GMH, ∴MN=MH.
的值为
(3)不可能.
∵∠EDF=45°, 易证EM=AE+CN, 若 则
又在△BEM中, 又EM>BE+BM , ∴不可能.
4. 解析: (1) ∵∠B=90°, ∴∠BAE+∠AEB=90°,∵∠AEF=90°, ∴∠AEB+∠FEG=90°, ∴∠BAEE=∠FEG,又∠B=90°=∠EGF, ∴△ABE∽△EGF.
(2) 设CG=x, 则FG=x, 设BE=y, 则CE=10-y,∵△ABE∽△EGF, ∴FGBE=EGA,代入得: 整理的:(x-y)(y+10)=0,解得:x=y,即△ABE≌△EGF,若EC=2, 则B 即△CEF的面积为8.
(3) 设EC=m, 则BE=10-m, FG=10-m,
∴当EC=5时, △CEF的面积最大.
5.C.
解析: 易证△CBE≌△EHF, ∴△CEF是等腰直角三角
形, 故结论①正确;
∵∠ECG=45°, 由半角模型可得EG=BE+DG, ∴△AEG的周长为2AD=8, 故结论②正确;
由半角模型可得EG=DG+BE, 但. 故结论③错误.
综上, 选C.
①④
6.解析: 过点 F作FH⊥BA交BA延长线于点 H,
∵∠HAF=45°且∠H=90°,
∴△AHF 是等腰直角三角形, 又AF= BE, ∴HF=BE, EH=EA+AH=EA+BE=AB=CB,
∴△EHF≌△CBE, ∴EC=EF, 且易证∠CEF=90°,
∴△CEF 是等腰直角三角形, ∴∠ECF=45°,故结论①正确;
由半角模型可得, 当∠ECG=45°时, EG=BE+DG,∴C△AEG=AE+AG+EG=AE+AG+BE+DG=2a,故结论②错误;由半角模型得: 故结论③错误;
设BE= ma, 则AH=FH= ma,
当 时,可得△AEF面积的最大值为 故结论④正确.
综上,正确的结论有①④.
第3节 当半角遇上三垂直
前言:在第2章中的半角模型和三垂直模型都有正方形的身影,把这两个模型结合起来,问题将变得更有趣.
知 识 导 航
1 模型回顾
(1) 三垂直模型
(2) 半角模型
引例1:如图,四边形ACDF 是正方形,∠CEA和∠ABF都是直角且点 E、A、B三点共线, AB=4, 则阴影部分的面积是 .
解析: 由题意得△CEA≌△ABF, ∴CE=AB=4,
当半角遇上三垂直
引例2:如图,在正方形ABCD中, E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交 BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H, 连接BH.
(1) 求证: GF=GC;
(2) 用等式表示线段BH与AE的数量关系,并证明.
解析: (1) 连接DF, ∵△ADE和△DFE关于DE对称,
∴△DAE≌△DFE, ∴DF=DA=DC,在 Rt△DFG和Rt△DCG中,
∴△DGF≌△DGC(HL).
∴GF=GC.
∵△DAE≌△DFE, ∴∠ADE=∠FDE,
∵△FDG≌△CDG, ∴∠FDG=∠CDG,
在△DAE和△EQH中,
∴△DAE≌△EQH(AAS),
∴AE=QH, DA=EQ,
又∵AB=DA=EQ, ∴AE=BQ,
∴BQ=HQ, ∴△BQH是等腰直角三角形,
模型总结
本题巧妙地将半角与三垂直结合在一张图中,条件与结论的巧妙组合,还可以有更多变形.
在引例2的图中,除了正方形条件外,其实还存在另外三个条件与结论:
(1)∠DEH=90°;(2)∠EDH=45°;(3)∠CBH=45°.
其中任意两个组合均可得到第三个,引例2是由(1)、(2) 结合得到(3).
变式1: 由 (1)、(3) → (2)
如图,在正方形ABCD中,E是AB边上一点,过点E作EH⊥DE, 连接BH, ∠CBH=45°, 求证: ∠EDH=45°.
解析:可以采用构造三垂直思路,但是对于△DAE和△EQH,并没有已知的相等线段,此路不通.
不同的条件下方法会不同,恰当地利用题目的已知条件,是解题的关键. 比如∠CBH=45°如何运用
证明: 在AD边上取点F使得AF=AE, 连接EF,
∴∠DFE=135°=∠EBH,
由题意可得: ∠FDE=∠BEH, DF=EB,
∴△DFE≌△EBH, ∴DE=DH,
∴△DEH是等腰直角三角形, ∴∠DEH=45°.
变式2: 由(2)、(3)→ (1)
如图,在正方形ABCD中,E是AB边上一点,∠EDH=∠CBH=45°, 求证: DE⊥EH.
证明: ∵∠EDH=45°, ∠EBH=90°+45°=135°,∴∠EDH+∠EBH=180°, ∴B、E、D、H四点共圆,连接BD, ∴∠DEH=∠DBH=90°,∴DE⊥EH.
引例3:如图, 在正方形ABCD中, E是DC边上一点,(与D、C不重合), 连接AE, 将△ADE沿AE所在的直线折叠得到△AFE, 延长EF交BC于 G, 连接AG,作 GH⊥AG, 与AE的延长线交于点 H, 连接CH. 显然 AE是∠DAF的平分线, EA是∠DEF的平分线. 仔细观察, 请逐一找出图中其他的角平分线(仅限于小于 180°的角平分线),并说明理由.
解析: (1) AG平分∠BAF;
(2) AG平分∠BGF;
(3) GH平分∠EGM;
(4) CH平分∠DCM.
以下证明:
(1) 由题意得: △AFG≌△ABG, ∴AG平分∠BAF;
(2) 同理, AG平分∠BGF;
(3)过点H作HN⊥BM,易证:△ABG≌△GNH,∴HN=BG,GN=AB, ∴BG=CN, ∴CN=HN, ∴△CNH是等腰直角三角形, ∴∠HCN=45°, ∴CH平分∠DCN;
(4) ∵∠AGH=90°, AG平分∠BGE,∴可证GH平分∠EGM.
真 题 演 练
1. 如图,在矩形ABCD中, AD=4, 点E在边 AD 上, 连接 CE, 以CE为边向右上方作正方形 CEFG,作FH⊥AD, 垂足为H, 连接AF.
(1) 求证: FH=ED;
(2) 当AE为何值时, △AEF的面积最大
2. 如图, 线段AB=8, 射线 BG⊥AB, P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F (点F与点A、B不重合).
(1) 求证: △AEP≌△CEP;
(2) 判断CF与AB 的位置关系,并说明理由;
(3) 求△AEF的周长.
3. 如图,在正方形ABCD中, 点E是AB边上一点, 以DE为边作正方形 DEFG, DF与BC交于点 M,延长EM交GF于点H, EF与CB交于点N, 连接CG.
(1) 求证: CD⊥CG;
(2) 若 求 的值;
(3) 已知正方形 ABCD 的边长为1, 点 E 在运动过程中,EM的长能否为 请说明理由.
4. 如图, 已知边长为10 的正方形ABCD,E是BC边上一动点(与B、C不重合), 连结AE, G是BC延长线上的点,过点 E作AE的垂线交. 的角平分线于点F, 若
(1)求证:
(2)若 求 的面积;
(3) 请直接写出EC为何值时, 的面积最大.
5. 如图, 正方形ABCD的边长为4, 点E在边AB上, BE=1, ∠DAM=45°, 点F在射线AM上,且 过点 F 作 AD 的平行线交 BA 的延长线于点 H,CF与AD 相交于点 G, 连接EC、EG、EF. 下列结论:
①△ECF的面积为
②△AEG的周长为8;
其中正确的是( )
A. ①②③ B. ①③
C. ①② D. ②③
6. 如图, 正方形ABCD的边长为a, 点E在边 AB 上运动(不与点A、B 重合), ∠DAM=45°, 点F在射线AM 上, 且 CF与AD 相交于点 G, 连接EC、EF、EG, 则下列结论:
①∠ECF=45°;
②△AEG的周长为
④△EAF的面积的最大值
其中正确的结论是 .(填写所有正确结论的序号)
第3节 当半角遇上三垂直
1. 解析: (1) 易证△EHF≌△CDE, ∴FH=ED.
(2) 设AE=x, 则DE=4-x, FH=DE=4-x,
当x=2时, S. AEF 取到最大值2,故当AE=2时, △AEF的面积最大.
2. 解析: (1) 在△AEP和△CEP中,
∴△APE≌△CEP (SAS).
(2) ∵△PAE≌△PCE, ∴∠PAE=∠PCE,又∠EAP=∠BAP, ∴∠PCE=∠BAP,
∵∠PCE+∠CPA=∠BAP+∠AFC, ∴∠AFC=∠CPA=90°,
∴CH⊥AB.
(3) CAAEF=AE+AF+EF=CE+EF+AF=CF+AF,过点C作CH⊥BG交BG于点H, 过点P作 PN⊥CF交CF.于点 N,
易证△ABP≌△PHC, ∴PH=AB=8, ∴CN=PH=8,又NF=PB=CH=BF, ∴AF+FN=AF+FB=AB=8,∴C△AEP=CF+AF=CN+NF=PH+AB=16,∴△AEF的周长为16.
3. 解析:(1)易证△DAE≌△DCG,∴∠DCG=∠DAE=90°,∴CD⊥CG.
(2) 易证∠MEN=∠MGF=∠CDG=∠ADE,易证△FME≌△FMG, ∴ME=MG, ∠FEM=∠FGM,
∴△EMN≌△GMH, ∴MN=MH.
的值为
(3)不可能.
∵∠EDF=45°, 易证EM=AE+CN, 若 则
又在△BEM中, 又EM>BE+BM , ∴不可能.
4. 解析: (1) ∵∠B=90°, ∴∠BAE+∠AEB=90°,∵∠AEF=90°, ∴∠AEB+∠FEG=90°, ∴∠BAEE=∠FEG,又∠B=90°=∠EGF, ∴△ABE∽△EGF.
(2) 设CG=x, 则FG=x, 设BE=y, 则CE=10-y,∵△ABE∽△EGF, ∴FGBE=EGA,代入得: 整理的:(x-y)(y+10)=0,解得:x=y,即△ABE≌△EGF,若EC=2, 则B 即△CEF的面积为8.
(3) 设EC=m, 则BE=10-m, FG=10-m,
∴当EC=5时, △CEF的面积最大.
5.C.
解析: 易证△CBE≌△EHF, ∴△CEF是等腰直角三角
形, 故结论①正确;
∵∠ECG=45°, 由半角模型可得EG=BE+DG, ∴△AEG的周长为2AD=8, 故结论②正确;
由半角模型可得EG=DG+BE, 但. 故结论③错误.
综上, 选C.
①④
6.解析: 过点 F作FH⊥BA交BA延长线于点 H,
∵∠HAF=45°且∠H=90°,
∴△AHF 是等腰直角三角形, 又AF= BE, ∴HF=BE, EH=EA+AH=EA+BE=AB=CB,
∴△EHF≌△CBE, ∴EC=EF, 且易证∠CEF=90°,
∴△CEF 是等腰直角三角形, ∴∠ECF=45°,故结论①正确;
由半角模型可得, 当∠ECG=45°时, EG=BE+DG,∴C△AEG=AE+AG+EG=AE+AG+BE+DG=2a,故结论②错误;由半角模型得: 故结论③错误;
设BE= ma, 则AH=FH= ma,
当 时,可得△AEF面积的最大值为 故结论④正确.
综上,正确的结论有①④.
同课章节目录
