2025年中考数学二轮专题复习 第3章 正方形压轴题讲练第4节 正方形综合 (含解析)
文档属性
| 名称 | 2025年中考数学二轮专题复习 第3章 正方形压轴题讲练第4节 正方形综合 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 163.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 07:29:32 | ||
图片预览


文档简介
第4节 正方形综合
前言:正方形综合题是几何压轴题的一种常见题型,在于正方形本身可以跟全等、相似、对称、旋转、勾股等等知识相结合,考点广、综合性强,需要扎实的知识基础以及恰当的方法选择.
真题演练
1. 如图, 点 P是正方形ABCD 的对角线BD延长线上的一点, 连接 PA, 过点 P作 PE⊥PA 交 BC的延长线于点E,过点E作EF⊥BP于点F,则下列结论中:
①PA=PE;
正确的是 .(填写所有正确结论的序号)
2. 如图, 在正方形ABCD中, 点E是边BC的中点, 连接AE、DE, 分别交BD、AC于点P、Q, 过点P作PF⊥AE交 CB 的延长线于F, 下列结论:
①∠AED+∠EAC+∠EDB=90°;
②AP=FP;
③
④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36;
⑤CE·EF=EQ·DE.
其中正确的结论有( )
中小学教育资源及组卷应用平台
A. 5个 B. 4个 C. 3个 D. 2个
3. 如图, 正方形ABCD的边长为2, 点E是BC的中点, AE与BD交于点 P, F是CD上一点, 连接AF分别交 BD, DE于点 M, N, 且AF⊥DE, 连接PN, 则以下结论中:
①
②
④△PMN∽△DPE.
正确的是( )
A. ①②③ B. ①②④
C. ①③④ D. ②③④
4. 如图, 正方形 ABCD, 点 F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M, 且交AD于点E,AC与DF交于点N,延长CB至 G,使 连接GM.有如下结论:
①DE=AF ;
②
③∠ADF=∠GMF;
上述结论中,所有正确结论的序号是( )
A. ①② B. ①③
C. ①②③ D. ②③④
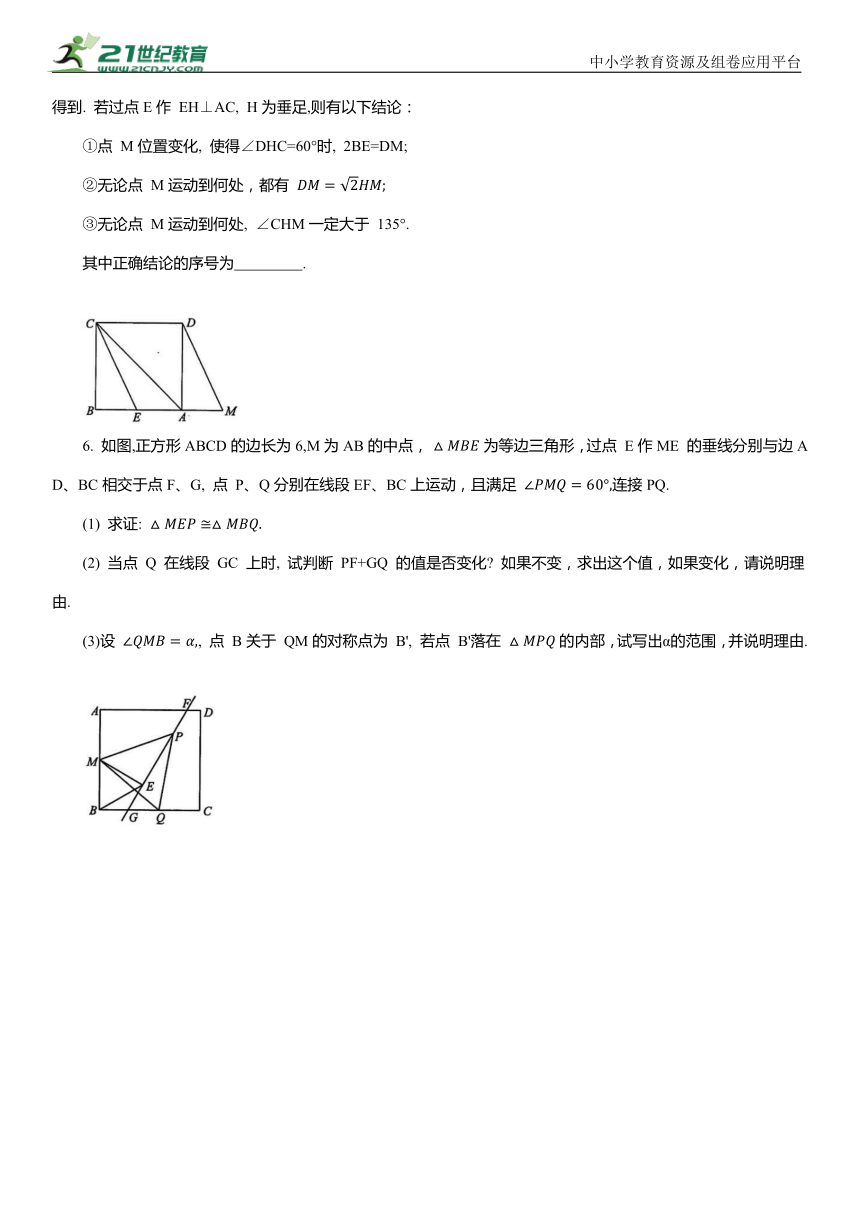
5. 如图, 已知正方形ABCD, 点M是边BA延长线上的动点(不与点A 重合),且AM①点 M位置变化, 使得∠DHC=60°时, 2BE=DM;
②无论点 M运动到何处,都有
③无论点 M运动到何处, ∠CHM一定大于 135°.
其中正确结论的序号为 .
6. 如图,正方形ABCD的边长为6,M为AB的中点, 为等边三角形,过点 E作ME 的垂线分别与边AD、BC相交于点F、G, 点 P、Q分别在线段EF、BC上运动,且满足 连接PQ.
(1) 求证:
(2) 当点 Q 在线段 GC 上时, 试判断 PF+GQ 的值是否变化 如果不变,求出这个值,如果变化,请说明理由.
(3)设 , 点 B关于 QM的对称点为 B', 若点 B'落在 的内部,试写出α的范围,并说明理由.
第4节 正方形综合
1.①②③.
解析: (1)过点P分别作 PM⊥BA、PN⊥BE, 交BA延长线于点 M, 交BE边于点N, 易证△PMA≌△PNE,∴PA=PE. 故结论①正确.
(2) 过点 P作 PG⊥BP交AD 延长线于点 G, 易证△PDG是等腰直角三角形,PD=PG,连接GE,易证△PDA≌△PGE,∴∠PGE=∠PDA=135°, ∴∠DGE=90°, ∴四边形 CDGE是矩形, 故结论②正确.
(3) 考虑到BF与PD无法直接相减,可转化线段.
故结论③正确.
(4) 易证△PDA≌△PGE, 显然 故结论④错误.
综上所述,正确的结论有①②③.
2. B.
解析: ∠AED+∠EAC+∠EDB=∠AOD=90°, ∴结论①正确;
连接PC, 则∠PCF=∠PAB=∠PFC, ∴PC=PF, 又PC=PA, ∴AP=FP, 故结论②正确;
设AO=m, 则 故结论③正确;
连接OE, 则 ∴正方形ABCD 面积为48, 故结论④错误;易证△EPF∽△ECD, 即
CE·EF=PE·ED, 又PE=QE,∴CE·EF=EQ·DE, 故结论⑤正确.
综上, 选B.
A.
3.解析:易证 即 故结论①正确;
考虑到 可得: 故结论③正确;
过点P作PH⊥AF交AF于点H, 由△APD∽△EPB, 可得:
又
故结论②正确;
∵PN≠DN, ∴∠PDN=∠DPN, ∴△PMN与△DPE不相似,故结论④错误.
综上, 选A.
4.C.
解析: 易证△CDE≌△DAF, ∴DE=AF, 故结论①正确;易证 结论②正确;
延长MF与CG延长线交于点Q,
则BQ=2AD, ∴CQ=3AD=3CB, 又
∴点G是CQ中点,
∴∠GCM=∠GMC, ∵∠ADF+∠GCM=90°,∠GMF+∠GMC=90°, ∴∠ADF=∠GMF, 故结论③正确;易证 则 故结论④错误.
综上, 选C.
5.①②③.
解析: 过点D作DO⊥AC交AC于点O, 设OH=a,若∠DHC=60°,则.
∴2BE=DM, 故结论①正确;
∵AM=BE, ∴EM=BA=AD, 又HE=HA, ∠HEM=∠HAD,
∴△HEM≌△HAD, ∴HM=HD, ∠EHM=∠AHD,
∴∠DHM=∠DHA-∠AHM=∠EHM-∠AHM=∠EHA=90°,
∴△DHM是等腰直角三角形, 故结论②正确;
∵∠DMH=∠DAH, ∴D、H、A、M四点共圆,
∴∠AHM=∠ADM,
∵∠ADM=∠BCE<45°, ∴∠AHM<45°,
∴∠CHM>135°,
故结论③正确;
综上,结论正确的有①②③.
6.解析: (1) ∵∠PMQ=∠BME=60°, ∴∠PME=∠BMQ,又∠MEP=90°=∠MBQ,ME=MB,∴△MEP≌△MBQ(ASA)
(2)设PE=m,则
(3)当点Q与点G重合时,点B 的对称点B'正好落在PQ边上, ∴α>30°,
当α>60°时,点B对称点落在三角形外,综上, 30°<α<60°时, 点B'落在△MPQ的内部.
前言:正方形综合题是几何压轴题的一种常见题型,在于正方形本身可以跟全等、相似、对称、旋转、勾股等等知识相结合,考点广、综合性强,需要扎实的知识基础以及恰当的方法选择.
真题演练
1. 如图, 点 P是正方形ABCD 的对角线BD延长线上的一点, 连接 PA, 过点 P作 PE⊥PA 交 BC的延长线于点E,过点E作EF⊥BP于点F,则下列结论中:
①PA=PE;
正确的是 .(填写所有正确结论的序号)
2. 如图, 在正方形ABCD中, 点E是边BC的中点, 连接AE、DE, 分别交BD、AC于点P、Q, 过点P作PF⊥AE交 CB 的延长线于F, 下列结论:
①∠AED+∠EAC+∠EDB=90°;
②AP=FP;
③
④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36;
⑤CE·EF=EQ·DE.
其中正确的结论有( )
中小学教育资源及组卷应用平台
A. 5个 B. 4个 C. 3个 D. 2个
3. 如图, 正方形ABCD的边长为2, 点E是BC的中点, AE与BD交于点 P, F是CD上一点, 连接AF分别交 BD, DE于点 M, N, 且AF⊥DE, 连接PN, 则以下结论中:
①
②
④△PMN∽△DPE.
正确的是( )
A. ①②③ B. ①②④
C. ①③④ D. ②③④
4. 如图, 正方形 ABCD, 点 F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M, 且交AD于点E,AC与DF交于点N,延长CB至 G,使 连接GM.有如下结论:
①DE=AF ;
②
③∠ADF=∠GMF;
上述结论中,所有正确结论的序号是( )
A. ①② B. ①③
C. ①②③ D. ②③④
5. 如图, 已知正方形ABCD, 点M是边BA延长线上的动点(不与点A 重合),且AM
②无论点 M运动到何处,都有
③无论点 M运动到何处, ∠CHM一定大于 135°.
其中正确结论的序号为 .
6. 如图,正方形ABCD的边长为6,M为AB的中点, 为等边三角形,过点 E作ME 的垂线分别与边AD、BC相交于点F、G, 点 P、Q分别在线段EF、BC上运动,且满足 连接PQ.
(1) 求证:
(2) 当点 Q 在线段 GC 上时, 试判断 PF+GQ 的值是否变化 如果不变,求出这个值,如果变化,请说明理由.
(3)设 , 点 B关于 QM的对称点为 B', 若点 B'落在 的内部,试写出α的范围,并说明理由.
第4节 正方形综合
1.①②③.
解析: (1)过点P分别作 PM⊥BA、PN⊥BE, 交BA延长线于点 M, 交BE边于点N, 易证△PMA≌△PNE,∴PA=PE. 故结论①正确.
(2) 过点 P作 PG⊥BP交AD 延长线于点 G, 易证△PDG是等腰直角三角形,PD=PG,连接GE,易证△PDA≌△PGE,∴∠PGE=∠PDA=135°, ∴∠DGE=90°, ∴四边形 CDGE是矩形, 故结论②正确.
(3) 考虑到BF与PD无法直接相减,可转化线段.
故结论③正确.
(4) 易证△PDA≌△PGE, 显然 故结论④错误.
综上所述,正确的结论有①②③.
2. B.
解析: ∠AED+∠EAC+∠EDB=∠AOD=90°, ∴结论①正确;
连接PC, 则∠PCF=∠PAB=∠PFC, ∴PC=PF, 又PC=PA, ∴AP=FP, 故结论②正确;
设AO=m, 则 故结论③正确;
连接OE, 则 ∴正方形ABCD 面积为48, 故结论④错误;易证△EPF∽△ECD, 即
CE·EF=PE·ED, 又PE=QE,∴CE·EF=EQ·DE, 故结论⑤正确.
综上, 选B.
A.
3.解析:易证 即 故结论①正确;
考虑到 可得: 故结论③正确;
过点P作PH⊥AF交AF于点H, 由△APD∽△EPB, 可得:
又
故结论②正确;
∵PN≠DN, ∴∠PDN=∠DPN, ∴△PMN与△DPE不相似,故结论④错误.
综上, 选A.
4.C.
解析: 易证△CDE≌△DAF, ∴DE=AF, 故结论①正确;易证 结论②正确;
延长MF与CG延长线交于点Q,
则BQ=2AD, ∴CQ=3AD=3CB, 又
∴点G是CQ中点,
∴∠GCM=∠GMC, ∵∠ADF+∠GCM=90°,∠GMF+∠GMC=90°, ∴∠ADF=∠GMF, 故结论③正确;易证 则 故结论④错误.
综上, 选C.
5.①②③.
解析: 过点D作DO⊥AC交AC于点O, 设OH=a,若∠DHC=60°,则.
∴2BE=DM, 故结论①正确;
∵AM=BE, ∴EM=BA=AD, 又HE=HA, ∠HEM=∠HAD,
∴△HEM≌△HAD, ∴HM=HD, ∠EHM=∠AHD,
∴∠DHM=∠DHA-∠AHM=∠EHM-∠AHM=∠EHA=90°,
∴△DHM是等腰直角三角形, 故结论②正确;
∵∠DMH=∠DAH, ∴D、H、A、M四点共圆,
∴∠AHM=∠ADM,
∵∠ADM=∠BCE<45°, ∴∠AHM<45°,
∴∠CHM>135°,
故结论③正确;
综上,结论正确的有①②③.
6.解析: (1) ∵∠PMQ=∠BME=60°, ∴∠PME=∠BMQ,又∠MEP=90°=∠MBQ,ME=MB,∴△MEP≌△MBQ(ASA)
(2)设PE=m,则
(3)当点Q与点G重合时,点B 的对称点B'正好落在PQ边上, ∴α>30°,
当α>60°时,点B对称点落在三角形外,综上, 30°<α<60°时, 点B'落在△MPQ的内部.
同课章节目录
