2025年中考数学二轮专题复习 第4章 圆 压轴题讲练第2节 动圆相切(一) (含解析)
文档属性
| 名称 | 2025年中考数学二轮专题复习 第4章 圆 压轴题讲练第2节 动圆相切(一) (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 296.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 07:35:08 | ||
图片预览




文档简介
第2节 动圆相切(一)
前言:“动圆相切问题”是动点与圆的结合,按运动的分式可分别“圆心为动点”、“直径为动线段”两大类,从不同的运动方式考虑恰当的方法得到相切.
中小学教育资源及组卷应用平台
知识导航
圆心为动点
切线判定:到圆心距离等于半径的直线是圆的切线.
即计算圆心到直线的距离d,当满足d=r时,即圆与直线相切.计算线段长度可考虑多用三角函数与相似三角形.
引例 1:如图,直线 l 的解析式为 点 P 坐标为(-4,0),以点P为圆心, 1为半径作圆, 当点 P 以每秒2个单位的速度向右移动时,时间t为何值时圆P 与直线l相切
解析: 过点 P作 PH⊥直线l, 垂足为H点, 当PH=r=1时,即可得圆P与直线l相切.
当点 P坐标为(-2, 0) 或(2, 0) 时, PH=1,
综上所述,t的值为1或3.
引例2: 在矩形ABCD中, AB=6, BC=8,点 O 在对角线 AC 上, 圆 O 的半径为2, 如果⊙O 与矩形ABCD 的各边都没有公共点,那么线段AO长的取值范围是
解析:圆O的半径为2,可得AO取值范围是
直径为动线段
切线判定定理:过半径外端且垂直于该半径的直线是圆的切线.
根据相切得到的垂直关系确定直径或动点的位置,用三角函数表示线段长,由线段之间数量关系列方程得解.
引例3: 在矩形ABCD中, AB=4, BC=3, 连接BD, 点P 从D 点出发以每秒1个单位向点 C运动,点Q 从点 B 出发以每秒2个单位向点D 运动,当其中一个点到终点时另一点也停止运动. 以PQ 中点O为圆心,PQ 为直径作圆,运动时间t为何值时,圆O与BD相切
解析: 当PQ⊥BD时, 圆O与BD相切,
由题意得: DP=t, DQ=5-2t, 若PA⊥BD, 即 代入得: 解得: 故当t的值为 时, 圆O与BD相切.
真 题 演 练
1. 如图, 直线a⊥b, 垂足为H, 点P在直线b上, PH=4cm, O为直线b上一动点, 若以1cm为半径的⊙O与直线a相切,则OP 的长为 .
2.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交, 则b的取值范围是( )
3. 如图, 直线l: 与坐标轴交于A、B两点,点M(m,0)是x轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M 与直线l相切时,则m的值为 .
4如图, 直线 交x轴于点 A,交y轴于点B,点P是x轴上一动点,以点 P为圆心,以1个单位长度为半径作⊙P,当⊙P 与直线AB相切时,点P的坐标是 .
5. 如图, △AOB 中, ∠O=90°, AO=8cm,BO=6cm, 点 C从A 点出发, 在边 AO 上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O 点运动, 过 OC 的中点 E作 CD 的垂线 EF, 则当点C运动了 s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.
6. 如图, Rt△ABC 中, ∠C=90°, AC=12,点 D 在边 BC上, CD=5, BD=13. 点 P 是线段 AD 上一动点, 当半径为 6 的⊙P 与△ABC 的一边相切时, AP 的长为
7. 如图, 点A 的坐标是(a,0)(a<0), 点C是以OA为直径的⊙B上一动点,点A 关于点C的对称点为 P. 当点C在⊙B 上运动时,所有这样的点 P 组成的图形与直线 有且只有一个公共点,则a 的值等于 .
8. 如图,正方形ABCD的边长为8,M是AB的中点, P是 BC 边上的动点, 连结 PM, 以点 P 为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为 .
9. 已知如图:在平面直角坐标系xOy中,直线 与x轴、y轴分别交于A、B 两点, P 是直线AB上一动点,⊙P的半径为1.
(1) 判断原点O与⊙P的位置关系,并说明理由;
(2)当⊙P过点B时,求⊙P被y轴所截得的劣弧的长;
(3) 当⊙P与x轴相切时,求出切点的坐标.
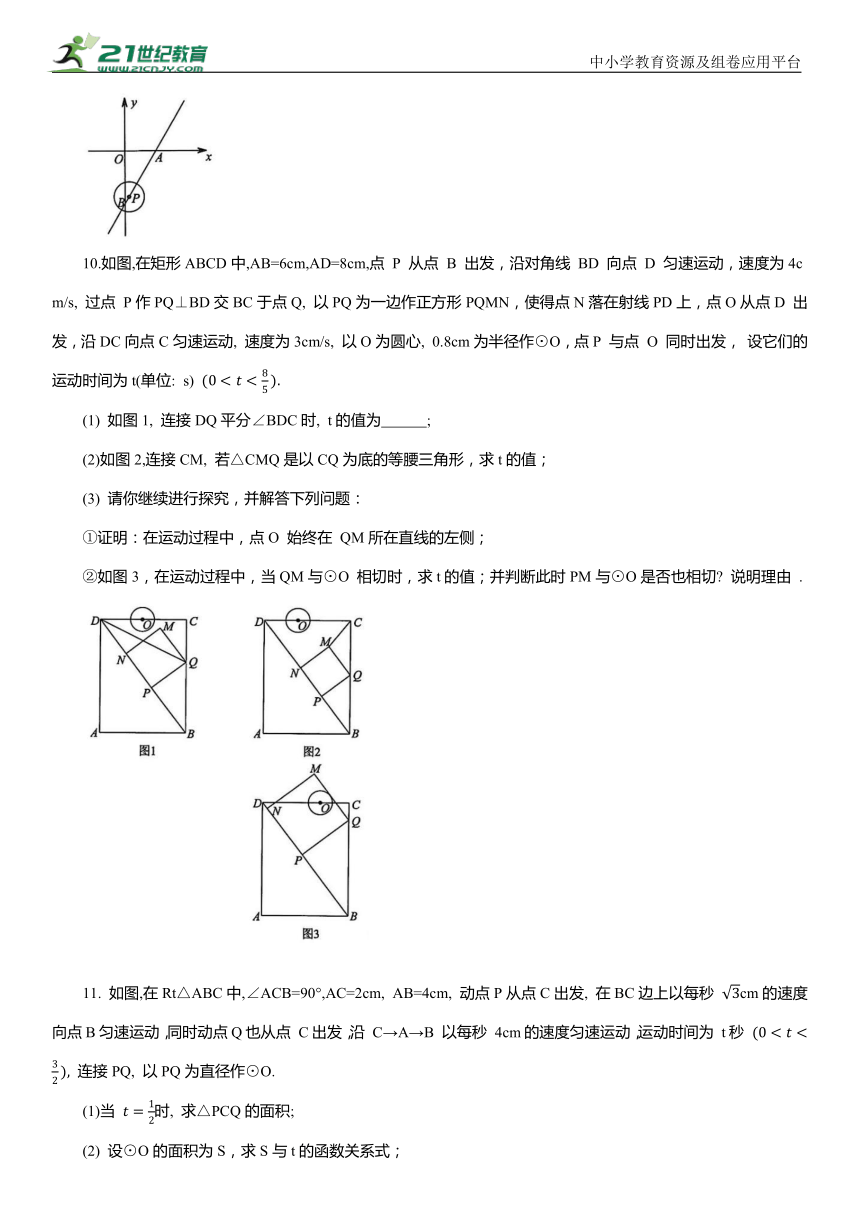
10.如图,在矩形ABCD中,AB=6cm,AD=8cm,点 P 从点 B 出发,沿对角线 BD 向点 D 匀速运动,速度为4cm/s, 过点 P作PQ⊥BD交BC于点Q, 以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D 出发,沿DC向点C匀速运动, 速度为3cm/s, 以O为圆心, 0.8cm为半径作⊙O,点P 与点 O 同时出发, 设它们的运动时间为t(单位: s)
(1) 如图1, 连接DQ平分∠BDC时, t的值为 ;
(2)如图2,连接CM, 若△CMQ是以CQ为底的等腰三角形,求t的值;
(3) 请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O 始终在 QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O 相切时,求t的值;并判断此时PM与⊙O是否也相切 说明理由 .
11. 如图,在Rt△ABC中,∠ACB=90°,AC=2cm, AB=4cm, 动点P从点C出发, 在BC边上以每秒 cm的速度向点B匀速运动,同时动点Q也从点 C出发,沿 C→A→B 以每秒 4cm的速度匀速运动,运动时间为 t秒 连接PQ, 以PQ为直径作⊙O.
(1)当 时, 求△PCQ的面积;
(2) 设⊙O的面积为S,求S与t的函数关系式;
(3)当Q在AB上运动时, ⊙O与 Rt△ABC的一边相切,求t的值.
第2节 动圆相切(一)
1.3cm或5cm.
2 D.
解析:确定两个相切的时刻,当 时,直线与圆相切,故若直线与圆相交,则b的取值范围是 故选 D.
3. 或
解析:点M 到直线l的距离为2,即可得圆 M 与直线l相切. 过点M作MH⊥AB交AB于H点, 当圆M与直线l相切时,MH=r=2, tan∠ABO= , ∴BH=4, BM=2
M点在B点左侧时,点M坐标为(2-2 ,0),
M点在B点右侧时,点M坐标为(2+2 ,0),
综上,m的值为 或
4.或(- ,0)
解析: 若圆 P与AB 相切, 则点 P 到直线AB 的距离为1,
可得 又点A坐标为(-4, 0),
故点 P坐标为 或(- ,0).
5解析: 易证CD∥AB, 当圆C与直线EF相切时,
6.
解析: 当圆 P与BC边相切时, 过点 P作PH⊥BC交BC,则 PH=6, 易证△DHP∽△DCA, DPDA=PH=C= 解得:
当圆P与AB边相切时, 过点 P作PM⊥AB 交AB于 M点,则PM=6, 过点D作DN⊥AB交AB于点N, 易证△BND∽△BCA, 可得: 解得: 易证△AMP∽△AND, 解得: 综上,AP 的长为 或:
解析:确定点 P轨迹,考虑AP=2AC始终成立,可得点 P轨迹是以点O为圆心,OA为半径的圆,若圆与直线 相切,则半径等于点 O 到直线 的距离,用面积法可求 故 则
解析:圆不可能与AB、BC边相切.
当圆P与CD相切时, 即 PM=PC
如图所示, 设BP=x, 则. 则 解得: x=3.
当圆P与AD相切时, 即PM=r=8, 解得. 综上,BP的长为3或4
解析: (1) 过点 O 作 OH⊥AB 于点 H, 可得( ∴OH>r, 故点O在圆外.
(2)记圆P与y轴另外一交点为C,连接PC,则∠BPC=120°,则弧 故圆 P 被y轴截得的弧长为
(3)圆P与x轴相切,即点P到x轴距离为1即可,
当 时, 解得:
当 =1时, 解得:
故切点的坐标为 或
10. 解析:(1)由题意得: PB=4t, PQ=3t, BQ=5t, CQ=8-5t,.若DQ平分∠BDC, 则CQ=PQ, 即8-5t=3t, 解得: t=1,故t的值为1;
(2) 过点 M作MH⊥BC交BC边于点 H,
若△CMQ是以 CQ 为底的等腰三角形,则H为CQ 中点,则
易证 代入得: 解得: 故t的值为
(3)①由于点 O 与直线 MQ 均为运动的,可取对角线 BD为参照物. 过点 O 作 OE⊥BD 交 BD 于点 E, 则 OD=3t, 又 ∴OE②过点O作FG⊥BD交BD于点 F,则FG⊥MQ, 垂足记为G,
若圆O与四边形相切,
则 解得:
即当 时,圆与QM相切,
此时若圆O与MP 也相切, 则 MO平分∠PMQ,即tan∠OMG=tan22.5°,
又
又OG=r=0.8cm,
∴此时PM与圆O不相切.
11. 解析: (1)当 时,
(2)当 时,
当 时,
(3) 当点Q在AB上时, 当圆O与BC边相切时, 即PQ⊥BC,
代入得: 解得: t=1;当圆O与AB 相切时, 即PQ⊥AB,
代入得: 解得:
当圆O与AC边相切时, 过点O作 ON⊥AC交AC于点N,则
由 得:
解得: (舍).
故综上所述,t的值为1或 或.
前言:“动圆相切问题”是动点与圆的结合,按运动的分式可分别“圆心为动点”、“直径为动线段”两大类,从不同的运动方式考虑恰当的方法得到相切.
中小学教育资源及组卷应用平台
知识导航
圆心为动点
切线判定:到圆心距离等于半径的直线是圆的切线.
即计算圆心到直线的距离d,当满足d=r时,即圆与直线相切.计算线段长度可考虑多用三角函数与相似三角形.
引例 1:如图,直线 l 的解析式为 点 P 坐标为(-4,0),以点P为圆心, 1为半径作圆, 当点 P 以每秒2个单位的速度向右移动时,时间t为何值时圆P 与直线l相切
解析: 过点 P作 PH⊥直线l, 垂足为H点, 当PH=r=1时,即可得圆P与直线l相切.
当点 P坐标为(-2, 0) 或(2, 0) 时, PH=1,
综上所述,t的值为1或3.
引例2: 在矩形ABCD中, AB=6, BC=8,点 O 在对角线 AC 上, 圆 O 的半径为2, 如果⊙O 与矩形ABCD 的各边都没有公共点,那么线段AO长的取值范围是
解析:圆O的半径为2,可得AO取值范围是
直径为动线段
切线判定定理:过半径外端且垂直于该半径的直线是圆的切线.
根据相切得到的垂直关系确定直径或动点的位置,用三角函数表示线段长,由线段之间数量关系列方程得解.
引例3: 在矩形ABCD中, AB=4, BC=3, 连接BD, 点P 从D 点出发以每秒1个单位向点 C运动,点Q 从点 B 出发以每秒2个单位向点D 运动,当其中一个点到终点时另一点也停止运动. 以PQ 中点O为圆心,PQ 为直径作圆,运动时间t为何值时,圆O与BD相切
解析: 当PQ⊥BD时, 圆O与BD相切,
由题意得: DP=t, DQ=5-2t, 若PA⊥BD, 即 代入得: 解得: 故当t的值为 时, 圆O与BD相切.
真 题 演 练
1. 如图, 直线a⊥b, 垂足为H, 点P在直线b上, PH=4cm, O为直线b上一动点, 若以1cm为半径的⊙O与直线a相切,则OP 的长为 .
2.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交, 则b的取值范围是( )
3. 如图, 直线l: 与坐标轴交于A、B两点,点M(m,0)是x轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M 与直线l相切时,则m的值为 .
4如图, 直线 交x轴于点 A,交y轴于点B,点P是x轴上一动点,以点 P为圆心,以1个单位长度为半径作⊙P,当⊙P 与直线AB相切时,点P的坐标是 .
5. 如图, △AOB 中, ∠O=90°, AO=8cm,BO=6cm, 点 C从A 点出发, 在边 AO 上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O 点运动, 过 OC 的中点 E作 CD 的垂线 EF, 则当点C运动了 s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.
6. 如图, Rt△ABC 中, ∠C=90°, AC=12,点 D 在边 BC上, CD=5, BD=13. 点 P 是线段 AD 上一动点, 当半径为 6 的⊙P 与△ABC 的一边相切时, AP 的长为
7. 如图, 点A 的坐标是(a,0)(a<0), 点C是以OA为直径的⊙B上一动点,点A 关于点C的对称点为 P. 当点C在⊙B 上运动时,所有这样的点 P 组成的图形与直线 有且只有一个公共点,则a 的值等于 .
8. 如图,正方形ABCD的边长为8,M是AB的中点, P是 BC 边上的动点, 连结 PM, 以点 P 为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为 .
9. 已知如图:在平面直角坐标系xOy中,直线 与x轴、y轴分别交于A、B 两点, P 是直线AB上一动点,⊙P的半径为1.
(1) 判断原点O与⊙P的位置关系,并说明理由;
(2)当⊙P过点B时,求⊙P被y轴所截得的劣弧的长;
(3) 当⊙P与x轴相切时,求出切点的坐标.
10.如图,在矩形ABCD中,AB=6cm,AD=8cm,点 P 从点 B 出发,沿对角线 BD 向点 D 匀速运动,速度为4cm/s, 过点 P作PQ⊥BD交BC于点Q, 以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D 出发,沿DC向点C匀速运动, 速度为3cm/s, 以O为圆心, 0.8cm为半径作⊙O,点P 与点 O 同时出发, 设它们的运动时间为t(单位: s)
(1) 如图1, 连接DQ平分∠BDC时, t的值为 ;
(2)如图2,连接CM, 若△CMQ是以CQ为底的等腰三角形,求t的值;
(3) 请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O 始终在 QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O 相切时,求t的值;并判断此时PM与⊙O是否也相切 说明理由 .
11. 如图,在Rt△ABC中,∠ACB=90°,AC=2cm, AB=4cm, 动点P从点C出发, 在BC边上以每秒 cm的速度向点B匀速运动,同时动点Q也从点 C出发,沿 C→A→B 以每秒 4cm的速度匀速运动,运动时间为 t秒 连接PQ, 以PQ为直径作⊙O.
(1)当 时, 求△PCQ的面积;
(2) 设⊙O的面积为S,求S与t的函数关系式;
(3)当Q在AB上运动时, ⊙O与 Rt△ABC的一边相切,求t的值.
第2节 动圆相切(一)
1.3cm或5cm.
2 D.
解析:确定两个相切的时刻,当 时,直线与圆相切,故若直线与圆相交,则b的取值范围是 故选 D.
3. 或
解析:点M 到直线l的距离为2,即可得圆 M 与直线l相切. 过点M作MH⊥AB交AB于H点, 当圆M与直线l相切时,MH=r=2, tan∠ABO= , ∴BH=4, BM=2
M点在B点左侧时,点M坐标为(2-2 ,0),
M点在B点右侧时,点M坐标为(2+2 ,0),
综上,m的值为 或
4.或(- ,0)
解析: 若圆 P与AB 相切, 则点 P 到直线AB 的距离为1,
可得 又点A坐标为(-4, 0),
故点 P坐标为 或(- ,0).
5解析: 易证CD∥AB, 当圆C与直线EF相切时,
6.
解析: 当圆 P与BC边相切时, 过点 P作PH⊥BC交BC,则 PH=6, 易证△DHP∽△DCA, DPDA=PH=C= 解得:
当圆P与AB边相切时, 过点 P作PM⊥AB 交AB于 M点,则PM=6, 过点D作DN⊥AB交AB于点N, 易证△BND∽△BCA, 可得: 解得: 易证△AMP∽△AND, 解得: 综上,AP 的长为 或:
解析:确定点 P轨迹,考虑AP=2AC始终成立,可得点 P轨迹是以点O为圆心,OA为半径的圆,若圆与直线 相切,则半径等于点 O 到直线 的距离,用面积法可求 故 则
解析:圆不可能与AB、BC边相切.
当圆P与CD相切时, 即 PM=PC
如图所示, 设BP=x, 则. 则 解得: x=3.
当圆P与AD相切时, 即PM=r=8, 解得. 综上,BP的长为3或4
解析: (1) 过点 O 作 OH⊥AB 于点 H, 可得( ∴OH>r, 故点O在圆外.
(2)记圆P与y轴另外一交点为C,连接PC,则∠BPC=120°,则弧 故圆 P 被y轴截得的弧长为
(3)圆P与x轴相切,即点P到x轴距离为1即可,
当 时, 解得:
当 =1时, 解得:
故切点的坐标为 或
10. 解析:(1)由题意得: PB=4t, PQ=3t, BQ=5t, CQ=8-5t,.若DQ平分∠BDC, 则CQ=PQ, 即8-5t=3t, 解得: t=1,故t的值为1;
(2) 过点 M作MH⊥BC交BC边于点 H,
若△CMQ是以 CQ 为底的等腰三角形,则H为CQ 中点,则
易证 代入得: 解得: 故t的值为
(3)①由于点 O 与直线 MQ 均为运动的,可取对角线 BD为参照物. 过点 O 作 OE⊥BD 交 BD 于点 E, 则 OD=3t, 又 ∴OE
若圆O与四边形相切,
则 解得:
即当 时,圆与QM相切,
此时若圆O与MP 也相切, 则 MO平分∠PMQ,即tan∠OMG=tan22.5°,
又
又OG=r=0.8cm,
∴此时PM与圆O不相切.
11. 解析: (1)当 时,
(2)当 时,
当 时,
(3) 当点Q在AB上时, 当圆O与BC边相切时, 即PQ⊥BC,
代入得: 解得: t=1;当圆O与AB 相切时, 即PQ⊥AB,
代入得: 解得:
当圆O与AC边相切时, 过点O作 ON⊥AC交AC于点N,则
由 得:
解得: (舍).
故综上所述,t的值为1或 或.
同课章节目录
