弧度制(两课时)
图片预览

文档简介
课件17张PPT。弧度制(一)一、知识回顾1、角度制的定义
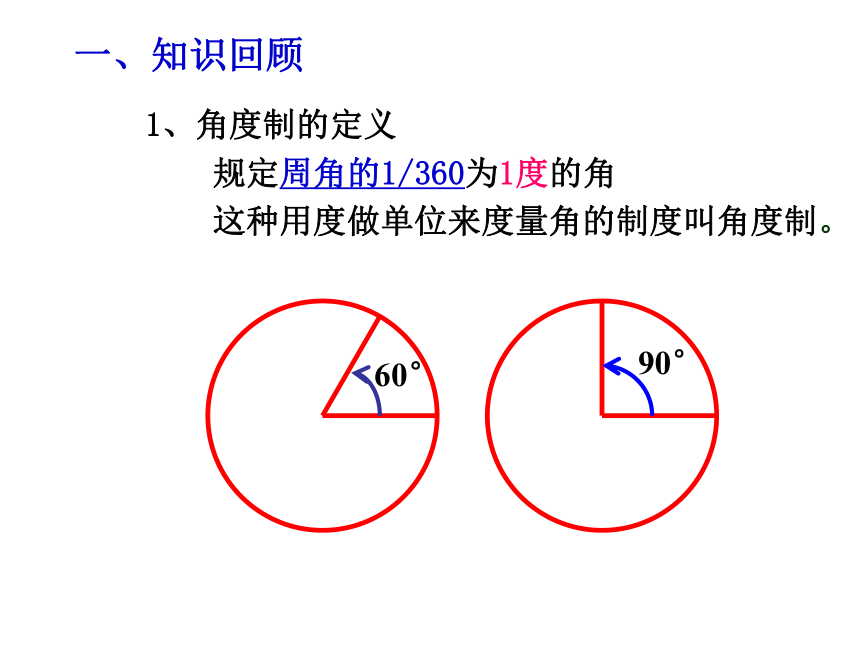
规定周角的1/360为1度的角
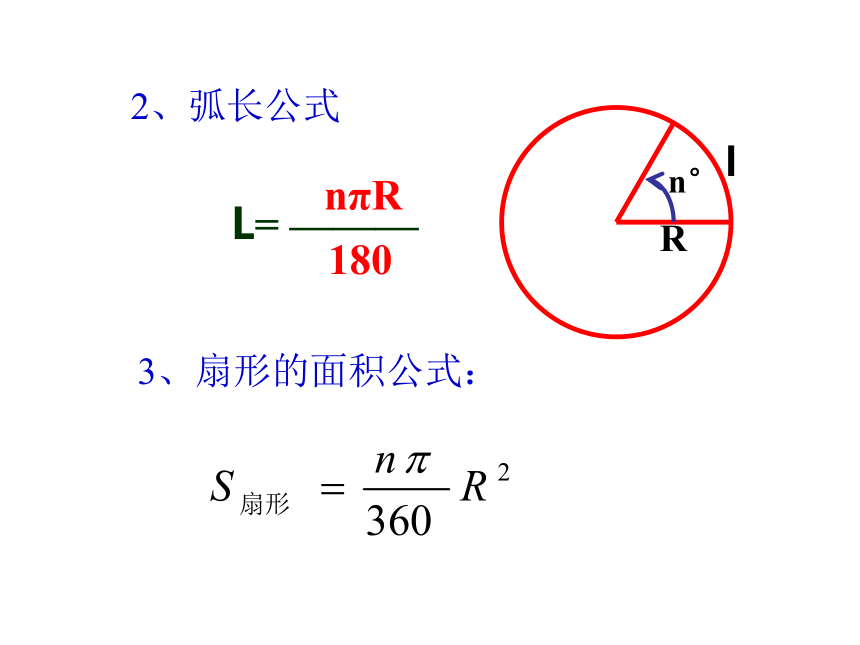
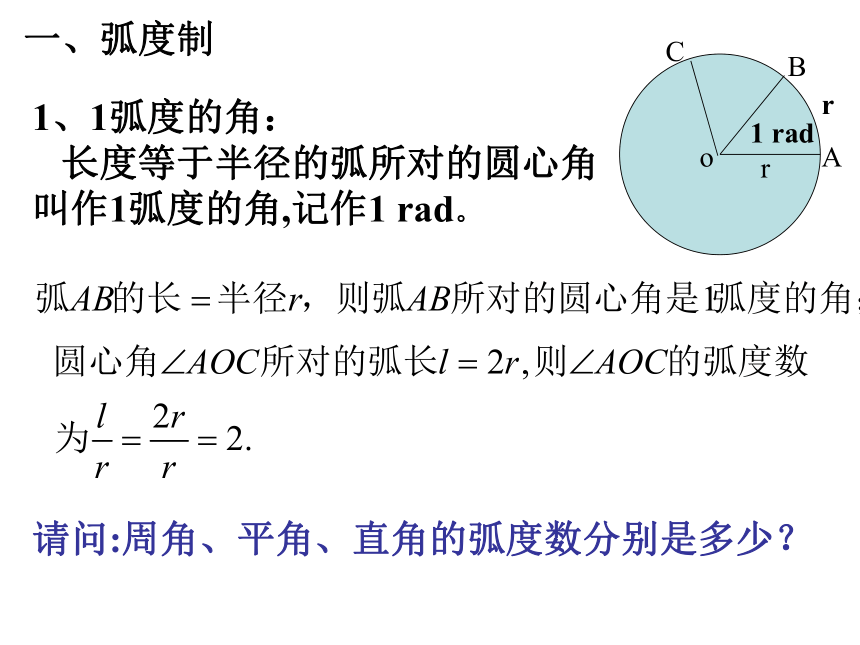
这种用度做单位来度量角的制度叫角度制。2、弧长公式3、扇形的面积公式:1、1弧度的角:
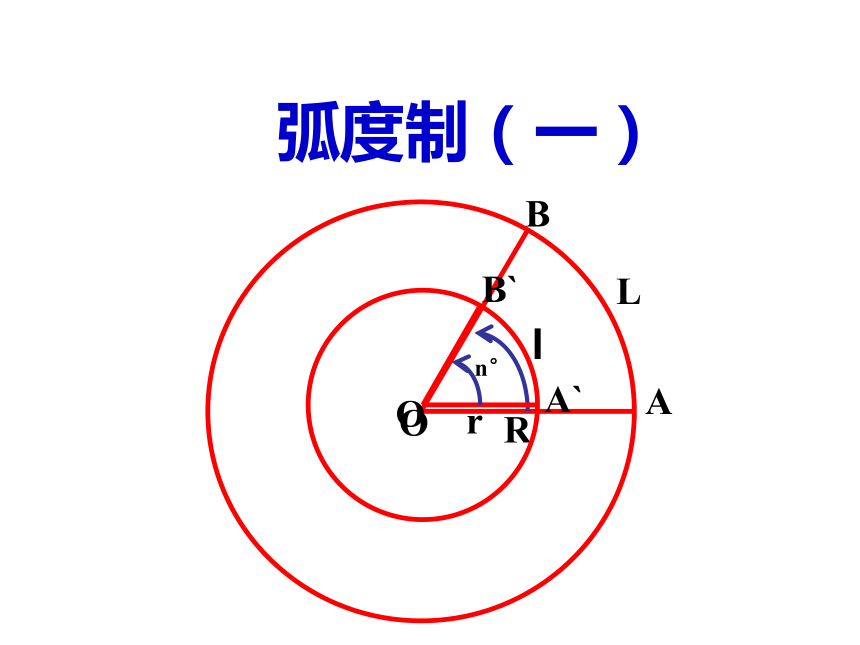
长度等于半径的弧所对的圆心角
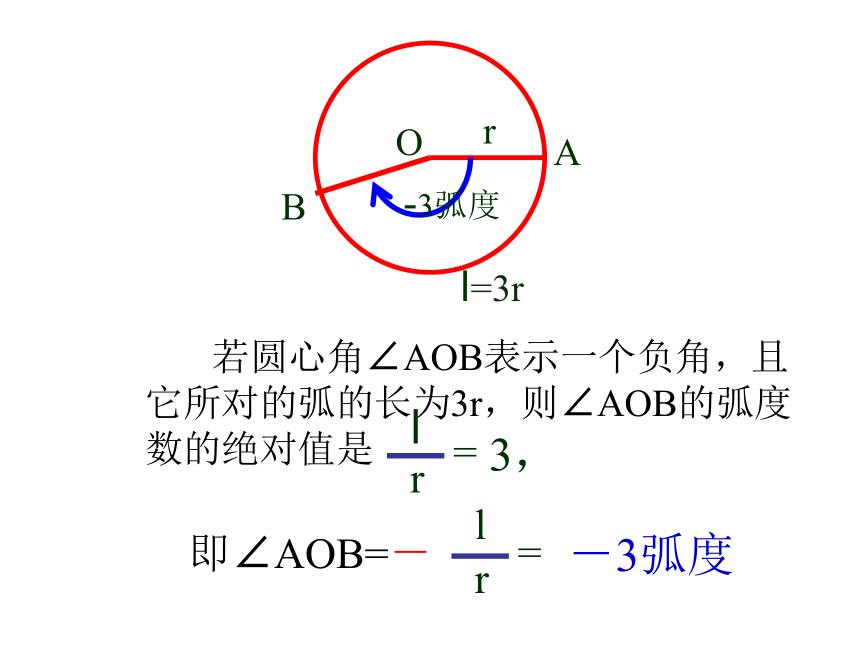
叫作1弧度的角,记作1 rad。一、弧度制oABrC请问:周角、平角、直角的弧度数分别是多少? 若圆心角∠AOB表示一个负角,且
它所对的弧的长为3r,则∠AOB的弧度
数的绝对值是-3弧度2、弧度制的定义:正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0;
在弧度制的定义中,我们是用弧长与其半径的比值来反映弧所对的圆心角的大小的。
为什么可以用这个比值来度量角的大小呢?这个比值与所取的圆的半径大小有没有关系?3、弧度与角度的换算A2π弧度2π弧度由180°= π 弧度 还可得180°= 1°× 180三、例题(1)把67°30′化成弧度。解: 解: 1、对于一些特殊角的度数与弧度数之间的换算要熟记。02、用弧度为单位表示角的大小时, “弧度”二字通常省略不写,但用“度”(°)为单位不能省。3、用弧度为单位表示角时,通常写 成“多少π”的形式。如无特别要求,不用将π化成小数。注意:练习:教材P11练习1、2、3、4锐角:{θ|0°<θ<90°},
直角: {θ|θ=90°}
钝角: {θ|90°<θ<180°}
平角: {θ|θ=180°}
周角: {θ|θ=360°}
0°到90°的角:{θ|0°≤θ<90°};
小于90°角:{θ|θ<90°}
0°到180°的角:{θ|0°≤θ<180°}
0°到360°的角:{θ|0°≤θ<360°}例2:请用弧度制表示下列角度的范围。例3:用弧度制表示
(1)终边落在45°角的终边上的所有角的集合(2)第Ⅱ象限角的集合基本关系导出关系三、小结: 3.特殊角的弧度数
规定周角的1/360为1度的角
这种用度做单位来度量角的制度叫角度制。2、弧长公式3、扇形的面积公式:1、1弧度的角:
长度等于半径的弧所对的圆心角
叫作1弧度的角,记作1 rad。一、弧度制oABrC请问:周角、平角、直角的弧度数分别是多少? 若圆心角∠AOB表示一个负角,且
它所对的弧的长为3r,则∠AOB的弧度
数的绝对值是-3弧度2、弧度制的定义:正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0;
在弧度制的定义中,我们是用弧长与其半径的比值来反映弧所对的圆心角的大小的。
为什么可以用这个比值来度量角的大小呢?这个比值与所取的圆的半径大小有没有关系?3、弧度与角度的换算A2π弧度2π弧度由180°= π 弧度 还可得180°= 1°× 180三、例题(1)把67°30′化成弧度。解: 解: 1、对于一些特殊角的度数与弧度数之间的换算要熟记。02、用弧度为单位表示角的大小时, “弧度”二字通常省略不写,但用“度”(°)为单位不能省。3、用弧度为单位表示角时,通常写 成“多少π”的形式。如无特别要求,不用将π化成小数。注意:练习:教材P11练习1、2、3、4锐角:{θ|0°<θ<90°},
直角: {θ|θ=90°}
钝角: {θ|90°<θ<180°}
平角: {θ|θ=180°}
周角: {θ|θ=360°}
0°到90°的角:{θ|0°≤θ<90°};
小于90°角:{θ|θ<90°}
0°到180°的角:{θ|0°≤θ<180°}
0°到360°的角:{θ|0°≤θ<360°}例2:请用弧度制表示下列角度的范围。例3:用弧度制表示
(1)终边落在45°角的终边上的所有角的集合(2)第Ⅱ象限角的集合基本关系导出关系三、小结: 3.特殊角的弧度数
