2025年中考数学压轴题二轮专题复习讲练第4讲 动态问题分析(含解析)
文档属性
| 名称 | 2025年中考数学压轴题二轮专题复习讲练第4讲 动态问题分析(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 763.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第4讲 动态问题分析
前言:动态问题伴随初中始终,从数轴上的动点,到坐标系中动点,从探究线段之间的关系,到探究特殊图形. 本讲介绍关于中考题中常见的动态问题题型. 了解题型,掌握方法,解决问题.
知 识 导 航
动点运动过程分析
此类问题中,一般有2张图,一张是动点所在的几何图形,另一张是与动点有关的函数图像. 解题思路参考引例1.
引例1: 如图1, 四边形ABCD中, AB∥CD, ∠ADC=90°,P从A 点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P 点的运动时间为 t秒,△PAD的面积为 S,S关于 t的函数图像如图2 所示,当P 运动到BC中点时, △PAD 的面积为 .
解析:一般分三步分析.
①确定函数关系中自变量、因变量的实际意义.
如图2,t表示动点 P 的运动时间,s表示△PAD的面积.
②将动点的运动过程与图像对应.
点P从A到B→第1段函数图像;
点 P从B到C→第2段函数图像;
点P从C到D→第3段函数图像.
③利用特殊点的坐标计算求值.
由横坐标6、10可得 CD=4,
t=6时,点 P到C点,s=8,即△ADC面积为8,可得AD=4,点P到B 点时, s=2, 即△ADB面积为2, 可得AB=1,∴BC=6-1=5. 当点P为BC中点时,
∴△PAD 的面积为5.
2重叠面积的计算
此类问题中,一般是某个图形位置在变化,由此产生两个图形重叠面积问题.
分析图形存在哪些可能的位置,分类讨论不同位置下的重叠部分面积.
引例2: 如图, 在等腰直角△ABC中, 于点 D, 点 P 从点 A 出发, 沿A→C 方向以 /s的速度运动到点 C停止,在运动过程中, 过点 P作PQ∥AB交BC于点Q, 以线段 PQ为边作等腰直角△PQM, 且∠PQM=90°(点 M、C 位于 PQ 异侧). 设点 P 的运动时间为x(s), △PQM与△ADC重叠部分的面积为y.
(1) 当点M落在AB上时, x= ;
(2) 当点M落在AD上时, x= ;
(3) 求y关于x的解析式,并写出自变量x的取值范围.
解析: (1) 当点M在AB上时, 点Q为BC中点,即点Q与点D重合时, 此时点P为AC中点, ∴x=4;(2) 当点M在AD上时, 即
(3)①当0②当 时,
化简得:
③当 时,
综上所述,
动点成特殊图形
此类问题中,一般考虑用代数法计算. 用时间t 或者其他量表示出相关线段,令相等列方程求解. 至于如何表示出线段,可考虑添加辅助线.
引例3: 如图1, 在矩形ABCD中, 动点 P从点A 出发, 以1cm/s的速度沿AD向终点D移动,设移动时间为t(s),连接PC, 以PC为一边作正方形 PCEF, 连接DE、DF, 设△PCD 的面积为y(cm ),y与t之间的函数关系如图2所示.
(1) AB= cm, AD= cm;
(2) 当t 为何值时,△DEF 的面积最小 请求出这个最小值;
(3) 当t 为何值时,△DEF 为等腰三角形 请简要说明理由.
解析:(1) AB=2cm, AD=5cm.
(2) 由题意得:
∵PD=5-t, CD=2,
∴当t=4时, △DEF的面积最小, 最小值为
(3)过点E作EM⊥CD交CD的延长线于点 M, 过点 F作FN⊥AD交AD于点 N,
由题意得△PDC≌△CME,
∴ME=DC=2, CM=PD=5-t,
由题意得: △FNP≌△PDC,
∴FN=PD=5-t, PN=CD=2, DN=|5-t-2|=|t-3|,
又
分类讨论:
①当DE=DF时, 即(
解得:t =3, t =7(舍);
②当DE=EF时, 即(
解得: t=4;
③当DF=EF时, 即(
解得:t =1, t =5;
综上所述,当t的值为1或3或4或5时,△DEF是等腰三角形.
真 题 演 练
1. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶. 图中折线表示快、慢两车之间的路程 y(km) 与它们的行驶时间 x
(h) 之间的函数关系. 小欣同学结合图像得出如下结论:
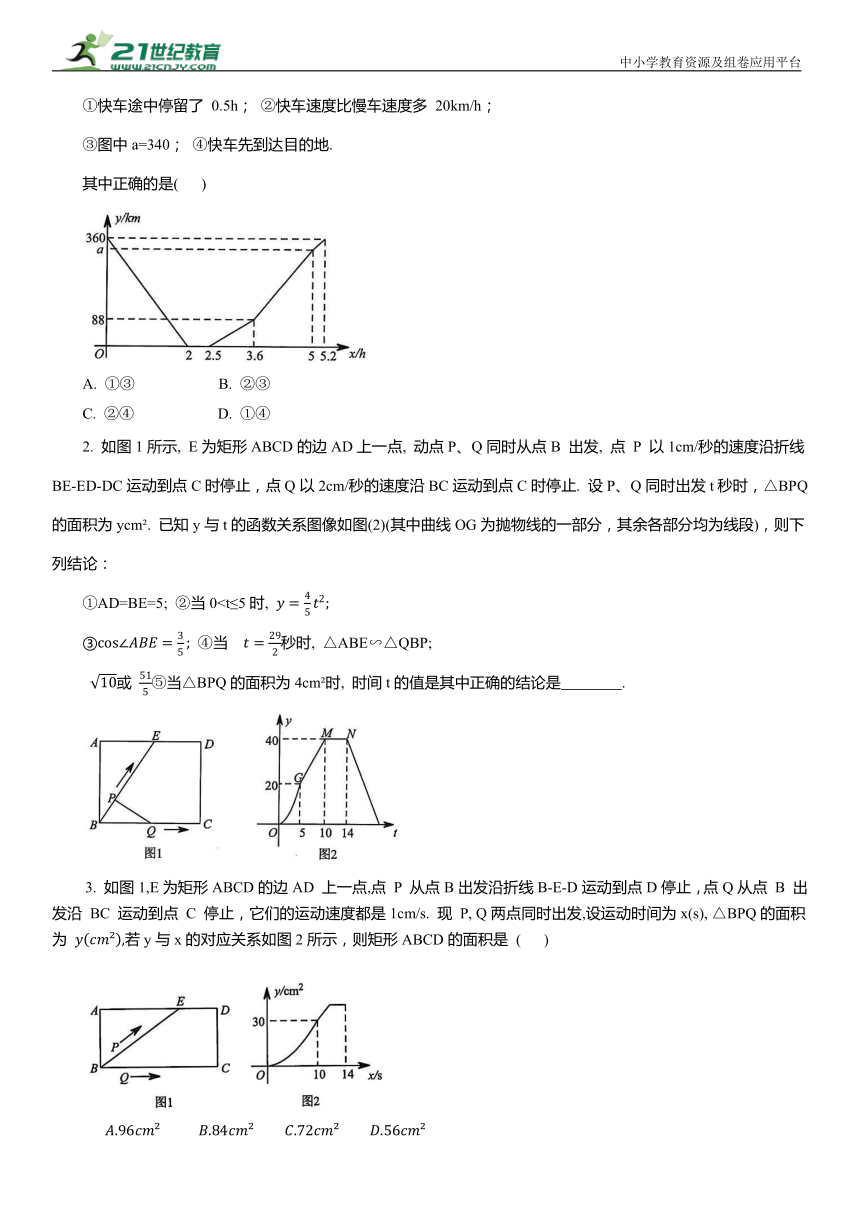
①快车途中停留了 0.5h; ②快车速度比慢车速度多 20km/h;
③图中a=340; ④快车先到达目的地.
其中正确的是( )
A. ①③ B. ②③
C. ②④ D. ①④
2. 如图1所示, E为矩形ABCD的边AD上一点, 动点P、Q同时从点B 出发, 点 P 以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止. 设P、Q同时出发t秒时,△BPQ的面积为ycm . 已知y与t的函数关系图像如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:
①AD=BE=5; ②当0③ ④当 秒时, △ABE∽△QBP;
或 ⑤当△BPQ的面积为4cm 时, 时间t的值是其中正确的结论是 .
3. 如图1,E为矩形ABCD的边AD 上一点,点 P 从点B出发沿折线B-E-D运动到点D停止,点Q从点 B 出发沿 BC 运动到点 C 停止,它们的运动速度都是1cm/s. 现 P, Q两点同时出发,设运动时间为x(s), △BPQ的面积为 若y与x的对应关系如图2所示,则矩形ABCD的面积是 ( )
4. 如图,在 中, 于点 G,点D为BC边上一动点, 交射线CA 于点 E, 作 关于 DE 的轴对称图形得到 设CD 的长为x, 与 重合部分的面积为y. 下列图像中,能反映点D从点C向点B运动过程中,y与x的函数关系的是( )
5. 如图1, 在四边形ABCD中, AB=2CD. 动点P从点A 出发, 在四边形ABCD的边上沿A→B→C的方向以1cm/s的速度匀速移动,到达点 C时停移动. 已知△APD的面积S(cm )与点P运动的时间t(s)之间的函数图像如图2所示,根据题意解答下列问题:
(1) 在图1中, AB= cm, BC= cm;
(2)如图3, 设动点P用了t (s)到达点P 处,用了 到达点P 处,分别过P 、P 作AD的垂线,垂足为 H . 当 时,求 的值.
6. 如图1, 在矩形 ABCD中, 点 P 从 B 点出发沿着四边按B→C→D→A 方向运动,开始以每秒 m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后又恢复为每秒m个单位匀速运动. 在运动过程中, 的面积S与运动时间t的函数关系如图2所示.
(1) 求矩形ABCD的长和宽;
(2) 求m、a、b的值.
7. 如图1, 在矩形ABCD中, AB=12cm, BC=6cm, 点P从A点出发, 沿A→B→C→D路线运动, 到D 点停止:点Q从D点出发, 沿D→C→B→A运动, 到A 点停止. 若点 P、点Q同时出发,点P 的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点 P、点 Q 同时改变速度,点P的速度变为每秒b(cm), 点Q 的速度变为每秒c(cm),如图2是△APD的面积S (cm )与点P出发时间x(秒)之间的关系: 图3是△AQD的面积S (cm ) 与Q点出发时间x(秒) 之间的关系,根据图像回答下列问题:
(1) 则a= ; b= ; c= .
(2) 设点 P出发x(秒)后离开点A 的路程为y(cm), 请写出y与x的关系式,并求出点P与Q相遇时x的值.
8. 如图1, B、D分别是x轴和y轴的正半轴上的点, AD∥x轴, AB∥y轴(AD>AB), 点 P从C点出发, 以3cm/s的速度沿C-D-A-B匀速运动,运动到B点时终止; 点Q从B 点出发, 以2cm/s的速度, 沿B-C-D匀速运动, 运动到D 点时终止. P、Q两点同时出发,设运动的时间为 t(s),△PCQ 的面积为 S(cm ), S与t之间的函数关系由图2 中的曲线段OE, 线段EF、FG表示.
(1) 求A、D点的坐标;
(2) 求图2中线段 FG的函数关系式;
(3)是否存在这样的时间t,使得△PCQ为等腰三角形 若存在,直接写出t的值; 若不存在,请说明理由.
9. 如图1, 在△ABC中, ∠A=120°, AB=AC, 点 P、Q同时从点 B 出发,以相同的速度分别沿折线B→A→C、射线BC运动, 连接PQ. 当点P到达点C时, 点 P、Q同时停止运动. 设BQ=x, △BPQ与△ABC重叠部分的面积为S. 如图 2 是 S 关于 x 的函数图像(其中0≤x≤8, 8(1) 填空: m的值为 ;
(2) 求S关于x的函数关系式,并写出x的取值范围;
(3) 请直接写出△PCQ为等腰三角形时x的值.
10. 如图1,矩形ABCD, 动点E从B 点出发匀速沿着边 BA向 A 点运动,到达 A 点停止运动,另一动点 F 同时从 B 点出发以 3cm/s 的速度沿着边 BC--CD - DA 运动, 到达 A 点停止运动.设E点运动时间为x(s),△BEF的面积为y(cm ). y关于x的函数图像如图2所示.
点E的运动速度是 cm/s;
(2) 求y关于x的函数关系及其自变量取值范围;
(3) 当∠DFE=90°时, 请直接写出x的取值.
11. 如图(1) 放置两个全等的含有 30°角的直角三角板ABC与DEF(∠B=∠E=30°), 若将三角板ABC 向右以每秒 1个单位长度的速度移动(点C 与点 E 重合时移动终止),移动过程中始终保持点B、F、C、E在同一条直线上, 如图(2), AB与DF、DE分别交于点 P、M, AC与DE交于点 Q,其中 设三角板ABC移动时间为x秒.
(1)在移动过程中,试用含x的代数式表示△AMQ的面积;
(2)计算x等于多少时,两个三角板重叠部分的面积有最大值 最大值是多少
12. 如图1,直线y= kx+1与x轴、y轴分别相交于点A、B,将△AOB 绕点 A 顺时针旋转, 使 AO 落在 AB 上, 得到△ACD,将△ACD沿射线BA平移,当点D到达x轴时运动停止. 设平移距离为m,平移后的图形在x轴下方部分的面积.为S, S关于m的函数图像如图2所示(其中0(1) 填空: a= , k= ;
(2) 求S关于m的解析式,并写出m的取值范围.
13. 如图, 在△ABC中, AB=AC=5, D为AB上一动点,D 点从A 点以 1个单位/秒的速度向 B 点运动,运动到 B 点即停止, 经过D 点作 DE∥BC, 交AC于点 E, 以DE为一边在 BC一侧作正方形 DEFG,在D 点运动过程中,设正方形 DEFG与△ABC的重叠面积为S,运动时间为t秒,如图2是s与t的函数图像.
(1) 求BC的长;
(2) 求a的值;
(3) 求S与t的函数关系式.
14. 如图,△ABC是等边三角形,AB=4cm,动点P从点A出发,以2cm/s的速度沿AB向点B匀速运动,过点 P作 PQ⊥AB, 交折线AC-CB 于点 Q, 以PQ为边作等边三角形 PQD,使点A,D在PQ异侧. 设点P的运动时间为x(s)(0(1) AP 的长为 cm(用含x的代数式表示).
(2) 当点D落在边BC上时, 求x的值.
(3) 求y关于x的解析式,并写出自变量x的取值范围.
15. 如图在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(3,4),平行于对角线AC 的直线 m从原点 O 出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与菱形OABC的两边分别交于点 M、N,直线m运动的时间为t(秒).
(1) 求点B 的坐标;
(2) 当 时,求t的值;
(3) 设△OMN的面积为 S, 求 S与t的函数表达式, 并确定S的最大值.
16. 如图, 正方形 OABC 的顶点 O 在坐标原点, 顶点 A 的坐标为(4, 3)
(1)顶点C的坐标为( , ),顶点 B 的坐标为( , );
(2)现有动点P、Q分别从C、A同时出发,点 P沿线段CB向终点B 运动,速度为每秒1 个单位,点Q 沿折线A→O→C向终点C运动,速度为每秒k个单位,当运动时间为2秒时,以P、Q、C为顶点的三角形是等腰三角形,求此时k的值.
(3) 若正方形 OABC 以每秒 个单位的速度沿射线 AO 下滑,直至顶点C落到x轴上时停止下滑.设正方形OABC在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
17. 已知: 在直角坐标系中,点A (0, 6), B (8, 0), 点C是线段AB的中点, CD⊥OB交 OB 于点 D, Rt△EFH 的斜边 EH 在射线 AB 上, 顶点 F在射线AB的左侧, EF∥OA. 点E从点A 出发,以每秒1个单位的速度向点 B 运动,到点 B 停止. AE=EF,运动时间为t(秒).
(1) 在 Rt△EFH中, EF= , EH= ;F( , )(用含有t的代数式表示)
(2) 当点H与点 C重合时, 求t的值.
(3)设△EFH与△CDB 重叠部分图形的面积为S(S>0),求S与t的关系式;
(4) 求在整个运动过程中 Rt△EFH扫过的面积.
18.在 Rt△AOB中, P、M、分别是BA、BO边上的两个动点. 点M从点 B 出发,沿 BO 以1 单位/秒的速度向点 O 运动; 点P 从点 B 出发,沿BA以a单位/秒的速度向点A运动;P、M两点同时出发,任意一点先到达终点时,两点停止运动.设运动的时间为t.
(1)线段AP 的长度为 (用含a、t的代数式表示);
(2)如图1,连结PO、PM, 若a=1, △PMO的面积为S,试求S的最大值;
(3)如图2, 连结PM、AM, 试探究: 在点 P、M运动的过程中,是否存在某个时刻,使得△PMB 为直角三角形且△PMA 是等腰三角形 若存在,求出此时a和t的取值,若不存在,请说明理由.
19. 如图, 在矩形ABCD中, AB=3, BC=4. 动点 P从点A 出发沿AC 向终点C运动,同时动点Q 从点 B 出发沿BA向点A 运动,到达A 点后立刻以原来的速度沿AB返回. 点P,Q运动速度均为每秒 1个单位长度,当点 P到达点 C时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
(1) 求线段AC的长度;
(2)当点Q从B点向A点运动时(未到达A点),求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线为l:①当l经过点 A 时, 射线 QP交AD 于点 E, 求AE的长;
②当l经过点B时,求t的值.
20. 如图1,已知矩形ABCD中,AB=60cm, BC=90cm. 点P 从点A 出发, 以3cm/s 的速度沿AB运动: 同时, 点Q从点 B 出发, 以 20cm/s 的速度沿 BC运动. 当点 Q 到达点 C时,P、Q两点同时停止运动.设点 P、Q运动的时间为t(s).
(1) 当t= s时, △BPQ为等腰三角形;
(2) 当BD平分 PQ时, 求t的值;
(3)如图2, 将△BPQ 沿 PQ 折叠, 点 B 的对应点为 E,PE、QE分别与AD交于点F、G.
探索:是否存在实数t,使得AF=EF 如果存在,求出t的值:如果不存在,说明理由.
第4讲 动态问题分析
1.B.
解析: x=2时, 快车慢车相遇, 当2∴①错误; ②正确; ③正确; ④错误; 故选B.
2. ②④.
解析: 点 G: B点到了 C点; 点 M: P 点到了点 E; 点 N:P点到了点D;
可求AD=BE=10, 故结论①错误;
过点 P 作 PH⊥BC 交 BC 于点 H, 当当0故结论③错误;
当 时, 此时
∴△ABE∽△QBP, 故结论④正确;
结论⑤显然错误.
综上所述,正确的是②④.
3.C.
4.A.
解析: 当0当25.解析:(1) AB=6cm, BC=4cm;
(2) 过点 D 作 DM⊥AB, 则 AM=3, DM=4, ∴AD=5,
在△AP H 中,
∴P B=1, 连接P P , 则P P ∥AD,∴BP =
故 的值为
6..解析:(1) 由题意得, 当6≤t≤8时, 点P从C向D运动, 故CD=2×2=4,
当t=6时, 点P与点C重合,
故矩形ABCD的长为8, 宽为4.
(2)a秒时, 点P在BC中点处,
从a秒至6秒,点P运动了4秒,又点P速度为2个单位每秒,故a的值为4,
m=4÷4=1, b秒时, 点P距离A点2个单位, 故b=8+6+2=8+3=11,
故m的值为1; a的值为4; b的值为11.
7.解析: (1) 考虑当时间为a时, △APD面积为24,可得 a=8, 考虑接下来2秒运动了4cm, ∴b=2,对于点 C来说,整个运动过程时间为22s,
即2×8+c·(22-8)=30, ∴c=1,
综上, a=8, b=2, c=1;
(2) 当0当8综上,
当P、Q相遇时, 即8+8×2+3(x-8)=30, 解得: x=10,故10秒时, 点 P、Q相遇.
8.解析: (1) 点A坐标为(6, 3), 点D坐标为(0, 3);
(2)点F:Q到点 C,P到点.A,
(3)①当0②当1若PC=PQ,则CQ=2DP,即6-2t=2(3t-3),角解得:
若PQ=CQ, 过点 P 作 PH⊥BC交 BC 于点 H, 则 PH=3,HQ=|9-5t|, 则. 又CQ=6-2t,
整理得: ,∴方程无实根;
若 即 整理得:
解得: (舍),
③当3即:2(t-3)=2(12-3t),解得:
综上所述,当t的值为 或15/4时, △PCQ是等腰三角形.
9.解析: (1) 当x=m时, 点Q到了点 C, 故
(2)当0当 时,
当 时,
综上,
(3)当0当 时, PQ=CQ, 则
即 解得:
当 时, CP=CQ, 即 解得:
综上所述,当△PCQ 为等腰三角形时,x的值为 或
10. 解析: (1) 由图像可知当 x=1 时, 点 F 到达点 C, 故BC=3cm,
当x=2时, 点F到点D, ∴CD=3cm, ∴AB=3cm,x=1时,△BEF的面积为 又此时BF=3cm,∴BE=1cm,故点E的速度为1cm/s;
(2)当0当1当2综上所述,
(3) 当点F在BC上时, 易证△EBF∽△FCD,
当点F在 CD上时, 若CF=BE, 则∠EFD=90°,即3x-3=x, 解得:
综上, 当∠DFE=90°时, x的值为 或
11.解析: (1) 连接AD, 则AD=x, ∵MA=MD,
∴△AMQ是等边三角形,
即
当x=2时,重叠部分面积取到最大值,最大值是
12. 解析:(1)由函数图像可得AC=2,∴AO=2,∴k=- 当点D落在x轴上,此时平移的距离为4,∴a=4;
(2)当0当2综上所述,
13. 解析: (1) 当t=2 时, GF 边与 BC 边重合, 过点 A 作AH⊥DE交DE于点H, 则△AHD∽△DGB,
易证△ADE∽△ABC, ∴DEC=ADB= , ∴BC=6.
(2)t=2时, 故a的值为
(3)当0当2综上所述,
14. 解析: (1) AP=2x(cm).
(2) 当点D落在BC上时, 易证△PDB≌△QPA,
∴BP=AQ=2AP, 即
(3)当 时,
当 时,
当1综上,
15. 解析:(1)∵点C坐标为(3,4),∴OC=5,∴CB=OC=5,∴点B坐标为(8, 4).
(2)当M、N分别为OA、OC中点或M、N分别为AB、CB中点时,
当M为OA中点时,
当N为CB中点时,
综上,当 时,t的值为 或
(3)当0则 又OM=ON=t,
当5由题意可得: OD=t, 点N到x轴距离为4,
由题意可得: AM=AD=t-5,
综上,
当t=5时, S取到最大值10.
16.解析: (1) 点C坐标为(-3,4), 点B 坐标为(1,7);
(2) 当t=2时, CP=2, 且CP≠PQ,
当CP=CQ时, CQ=2, 点Q 的路程为5+3=8, 故k=4;当CQ=PQ时,点Q在CP的垂直平分线上,OQ=1,则AQ=4,∴k=2.
综上所述,k的值为4或2.
(3)当0当3综上,
17解析:(1) EF=AE=t;
点F坐标为
解得:
∴当t的值为 时,点H与点C重合.
(3) ①当 时,
②当 时,
③当5综上所述,
(4) 如图, △AFH即为扫过的面积, 故运动过程中,△EFH扫过的面积为
18.解析: (1) 5-at;
(2) 过点P作PH⊥OB交OB于点H, 则
当t=2时,S取到最大值
(3) 若∠PMB=90°且PM=PA,
此时 即 解得:
若∠BPM=90°且PM=PA,则
此时 即 解得: 综上,
19.解析: (1) AC=5;
(2)过点P作PG⊥AB交AB于点H,则
又AQ=AB-BQ=3-t,
(3)①直线l经过点A, 即AQ=AP,
情况1: 当0此时
过点Q作QO∥AD, 易证点O为AC中点, ∴OP=1,
易证∠△APE∽△OPQ,∴AEO=AP= 又 ∴AE=3
情况2: 当3≤t<5时, AP≠AQ.
综上,直线l过点A时,AE的值为3.
②当直线l经过点B时, 连接BP, 则BQ=BP,
情况1: 当0情况2: 当3≤t<5时, 过点P作PH⊥BC交BC于点 H,
解得: 综上,t的值为 或.
20. 解析: (1) 若△BPQ为等腰三角形, 则BP=BQ,
由题意得: BP=60-3t, BQ=20t,
∴60-3t=20t, 解得:
故 时,△BPQ为等腰三角形;
(2)若BD平分 PQ,则 即 解得: 故当BD平分PQ时,t的值为
(3) 若AF=EF, 则△AFP∽△EFG, 可得AG=EP,
由题意得: AP=3t, AG=PE=PB=60-3t,
DG=90-(60-3t)=3t+30,
GQ=EQ-EG=20t-3t=17t,过点Q作QH⊥AD交AD于点 H,
则GH=3t+30-(90-20t)=23t-60,
又
代入得: 解得: (舍)
故当t=4时, AF=EF.
第4讲 动态问题分析
前言:动态问题伴随初中始终,从数轴上的动点,到坐标系中动点,从探究线段之间的关系,到探究特殊图形. 本讲介绍关于中考题中常见的动态问题题型. 了解题型,掌握方法,解决问题.
知 识 导 航
动点运动过程分析
此类问题中,一般有2张图,一张是动点所在的几何图形,另一张是与动点有关的函数图像. 解题思路参考引例1.
引例1: 如图1, 四边形ABCD中, AB∥CD, ∠ADC=90°,P从A 点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P 点的运动时间为 t秒,△PAD的面积为 S,S关于 t的函数图像如图2 所示,当P 运动到BC中点时, △PAD 的面积为 .
解析:一般分三步分析.
①确定函数关系中自变量、因变量的实际意义.
如图2,t表示动点 P 的运动时间,s表示△PAD的面积.
②将动点的运动过程与图像对应.
点P从A到B→第1段函数图像;
点 P从B到C→第2段函数图像;
点P从C到D→第3段函数图像.
③利用特殊点的坐标计算求值.
由横坐标6、10可得 CD=4,
t=6时,点 P到C点,s=8,即△ADC面积为8,可得AD=4,点P到B 点时, s=2, 即△ADB面积为2, 可得AB=1,∴BC=6-1=5. 当点P为BC中点时,
∴△PAD 的面积为5.
2重叠面积的计算
此类问题中,一般是某个图形位置在变化,由此产生两个图形重叠面积问题.
分析图形存在哪些可能的位置,分类讨论不同位置下的重叠部分面积.
引例2: 如图, 在等腰直角△ABC中, 于点 D, 点 P 从点 A 出发, 沿A→C 方向以 /s的速度运动到点 C停止,在运动过程中, 过点 P作PQ∥AB交BC于点Q, 以线段 PQ为边作等腰直角△PQM, 且∠PQM=90°(点 M、C 位于 PQ 异侧). 设点 P 的运动时间为x(s), △PQM与△ADC重叠部分的面积为y.
(1) 当点M落在AB上时, x= ;
(2) 当点M落在AD上时, x= ;
(3) 求y关于x的解析式,并写出自变量x的取值范围.
解析: (1) 当点M在AB上时, 点Q为BC中点,即点Q与点D重合时, 此时点P为AC中点, ∴x=4;(2) 当点M在AD上时, 即
(3)①当0
化简得:
③当 时,
综上所述,
动点成特殊图形
此类问题中,一般考虑用代数法计算. 用时间t 或者其他量表示出相关线段,令相等列方程求解. 至于如何表示出线段,可考虑添加辅助线.
引例3: 如图1, 在矩形ABCD中, 动点 P从点A 出发, 以1cm/s的速度沿AD向终点D移动,设移动时间为t(s),连接PC, 以PC为一边作正方形 PCEF, 连接DE、DF, 设△PCD 的面积为y(cm ),y与t之间的函数关系如图2所示.
(1) AB= cm, AD= cm;
(2) 当t 为何值时,△DEF 的面积最小 请求出这个最小值;
(3) 当t 为何值时,△DEF 为等腰三角形 请简要说明理由.
解析:(1) AB=2cm, AD=5cm.
(2) 由题意得:
∵PD=5-t, CD=2,
∴当t=4时, △DEF的面积最小, 最小值为
(3)过点E作EM⊥CD交CD的延长线于点 M, 过点 F作FN⊥AD交AD于点 N,
由题意得△PDC≌△CME,
∴ME=DC=2, CM=PD=5-t,
由题意得: △FNP≌△PDC,
∴FN=PD=5-t, PN=CD=2, DN=|5-t-2|=|t-3|,
又
分类讨论:
①当DE=DF时, 即(
解得:t =3, t =7(舍);
②当DE=EF时, 即(
解得: t=4;
③当DF=EF时, 即(
解得:t =1, t =5;
综上所述,当t的值为1或3或4或5时,△DEF是等腰三角形.
真 题 演 练
1. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶. 图中折线表示快、慢两车之间的路程 y(km) 与它们的行驶时间 x
(h) 之间的函数关系. 小欣同学结合图像得出如下结论:
①快车途中停留了 0.5h; ②快车速度比慢车速度多 20km/h;
③图中a=340; ④快车先到达目的地.
其中正确的是( )
A. ①③ B. ②③
C. ②④ D. ①④
2. 如图1所示, E为矩形ABCD的边AD上一点, 动点P、Q同时从点B 出发, 点 P 以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止. 设P、Q同时出发t秒时,△BPQ的面积为ycm . 已知y与t的函数关系图像如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:
①AD=BE=5; ②当0
或 ⑤当△BPQ的面积为4cm 时, 时间t的值是其中正确的结论是 .
3. 如图1,E为矩形ABCD的边AD 上一点,点 P 从点B出发沿折线B-E-D运动到点D停止,点Q从点 B 出发沿 BC 运动到点 C 停止,它们的运动速度都是1cm/s. 现 P, Q两点同时出发,设运动时间为x(s), △BPQ的面积为 若y与x的对应关系如图2所示,则矩形ABCD的面积是 ( )
4. 如图,在 中, 于点 G,点D为BC边上一动点, 交射线CA 于点 E, 作 关于 DE 的轴对称图形得到 设CD 的长为x, 与 重合部分的面积为y. 下列图像中,能反映点D从点C向点B运动过程中,y与x的函数关系的是( )
5. 如图1, 在四边形ABCD中, AB=2CD. 动点P从点A 出发, 在四边形ABCD的边上沿A→B→C的方向以1cm/s的速度匀速移动,到达点 C时停移动. 已知△APD的面积S(cm )与点P运动的时间t(s)之间的函数图像如图2所示,根据题意解答下列问题:
(1) 在图1中, AB= cm, BC= cm;
(2)如图3, 设动点P用了t (s)到达点P 处,用了 到达点P 处,分别过P 、P 作AD的垂线,垂足为 H . 当 时,求 的值.
6. 如图1, 在矩形 ABCD中, 点 P 从 B 点出发沿着四边按B→C→D→A 方向运动,开始以每秒 m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后又恢复为每秒m个单位匀速运动. 在运动过程中, 的面积S与运动时间t的函数关系如图2所示.
(1) 求矩形ABCD的长和宽;
(2) 求m、a、b的值.
7. 如图1, 在矩形ABCD中, AB=12cm, BC=6cm, 点P从A点出发, 沿A→B→C→D路线运动, 到D 点停止:点Q从D点出发, 沿D→C→B→A运动, 到A 点停止. 若点 P、点Q同时出发,点P 的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点 P、点 Q 同时改变速度,点P的速度变为每秒b(cm), 点Q 的速度变为每秒c(cm),如图2是△APD的面积S (cm )与点P出发时间x(秒)之间的关系: 图3是△AQD的面积S (cm ) 与Q点出发时间x(秒) 之间的关系,根据图像回答下列问题:
(1) 则a= ; b= ; c= .
(2) 设点 P出发x(秒)后离开点A 的路程为y(cm), 请写出y与x的关系式,并求出点P与Q相遇时x的值.
8. 如图1, B、D分别是x轴和y轴的正半轴上的点, AD∥x轴, AB∥y轴(AD>AB), 点 P从C点出发, 以3cm/s的速度沿C-D-A-B匀速运动,运动到B点时终止; 点Q从B 点出发, 以2cm/s的速度, 沿B-C-D匀速运动, 运动到D 点时终止. P、Q两点同时出发,设运动的时间为 t(s),△PCQ 的面积为 S(cm ), S与t之间的函数关系由图2 中的曲线段OE, 线段EF、FG表示.
(1) 求A、D点的坐标;
(2) 求图2中线段 FG的函数关系式;
(3)是否存在这样的时间t,使得△PCQ为等腰三角形 若存在,直接写出t的值; 若不存在,请说明理由.
9. 如图1, 在△ABC中, ∠A=120°, AB=AC, 点 P、Q同时从点 B 出发,以相同的速度分别沿折线B→A→C、射线BC运动, 连接PQ. 当点P到达点C时, 点 P、Q同时停止运动. 设BQ=x, △BPQ与△ABC重叠部分的面积为S. 如图 2 是 S 关于 x 的函数图像(其中0≤x≤8, 8
(2) 求S关于x的函数关系式,并写出x的取值范围;
(3) 请直接写出△PCQ为等腰三角形时x的值.
10. 如图1,矩形ABCD, 动点E从B 点出发匀速沿着边 BA向 A 点运动,到达 A 点停止运动,另一动点 F 同时从 B 点出发以 3cm/s 的速度沿着边 BC--CD - DA 运动, 到达 A 点停止运动.设E点运动时间为x(s),△BEF的面积为y(cm ). y关于x的函数图像如图2所示.
点E的运动速度是 cm/s;
(2) 求y关于x的函数关系及其自变量取值范围;
(3) 当∠DFE=90°时, 请直接写出x的取值.
11. 如图(1) 放置两个全等的含有 30°角的直角三角板ABC与DEF(∠B=∠E=30°), 若将三角板ABC 向右以每秒 1个单位长度的速度移动(点C 与点 E 重合时移动终止),移动过程中始终保持点B、F、C、E在同一条直线上, 如图(2), AB与DF、DE分别交于点 P、M, AC与DE交于点 Q,其中 设三角板ABC移动时间为x秒.
(1)在移动过程中,试用含x的代数式表示△AMQ的面积;
(2)计算x等于多少时,两个三角板重叠部分的面积有最大值 最大值是多少
12. 如图1,直线y= kx+1与x轴、y轴分别相交于点A、B,将△AOB 绕点 A 顺时针旋转, 使 AO 落在 AB 上, 得到△ACD,将△ACD沿射线BA平移,当点D到达x轴时运动停止. 设平移距离为m,平移后的图形在x轴下方部分的面积.为S, S关于m的函数图像如图2所示(其中0
(2) 求S关于m的解析式,并写出m的取值范围.
13. 如图, 在△ABC中, AB=AC=5, D为AB上一动点,D 点从A 点以 1个单位/秒的速度向 B 点运动,运动到 B 点即停止, 经过D 点作 DE∥BC, 交AC于点 E, 以DE为一边在 BC一侧作正方形 DEFG,在D 点运动过程中,设正方形 DEFG与△ABC的重叠面积为S,运动时间为t秒,如图2是s与t的函数图像.
(1) 求BC的长;
(2) 求a的值;
(3) 求S与t的函数关系式.
14. 如图,△ABC是等边三角形,AB=4cm,动点P从点A出发,以2cm/s的速度沿AB向点B匀速运动,过点 P作 PQ⊥AB, 交折线AC-CB 于点 Q, 以PQ为边作等边三角形 PQD,使点A,D在PQ异侧. 设点P的运动时间为x(s)(0
(2) 当点D落在边BC上时, 求x的值.
(3) 求y关于x的解析式,并写出自变量x的取值范围.
15. 如图在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(3,4),平行于对角线AC 的直线 m从原点 O 出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与菱形OABC的两边分别交于点 M、N,直线m运动的时间为t(秒).
(1) 求点B 的坐标;
(2) 当 时,求t的值;
(3) 设△OMN的面积为 S, 求 S与t的函数表达式, 并确定S的最大值.
16. 如图, 正方形 OABC 的顶点 O 在坐标原点, 顶点 A 的坐标为(4, 3)
(1)顶点C的坐标为( , ),顶点 B 的坐标为( , );
(2)现有动点P、Q分别从C、A同时出发,点 P沿线段CB向终点B 运动,速度为每秒1 个单位,点Q 沿折线A→O→C向终点C运动,速度为每秒k个单位,当运动时间为2秒时,以P、Q、C为顶点的三角形是等腰三角形,求此时k的值.
(3) 若正方形 OABC 以每秒 个单位的速度沿射线 AO 下滑,直至顶点C落到x轴上时停止下滑.设正方形OABC在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
17. 已知: 在直角坐标系中,点A (0, 6), B (8, 0), 点C是线段AB的中点, CD⊥OB交 OB 于点 D, Rt△EFH 的斜边 EH 在射线 AB 上, 顶点 F在射线AB的左侧, EF∥OA. 点E从点A 出发,以每秒1个单位的速度向点 B 运动,到点 B 停止. AE=EF,运动时间为t(秒).
(1) 在 Rt△EFH中, EF= , EH= ;F( , )(用含有t的代数式表示)
(2) 当点H与点 C重合时, 求t的值.
(3)设△EFH与△CDB 重叠部分图形的面积为S(S>0),求S与t的关系式;
(4) 求在整个运动过程中 Rt△EFH扫过的面积.
18.在 Rt△AOB中, P、M、分别是BA、BO边上的两个动点. 点M从点 B 出发,沿 BO 以1 单位/秒的速度向点 O 运动; 点P 从点 B 出发,沿BA以a单位/秒的速度向点A运动;P、M两点同时出发,任意一点先到达终点时,两点停止运动.设运动的时间为t.
(1)线段AP 的长度为 (用含a、t的代数式表示);
(2)如图1,连结PO、PM, 若a=1, △PMO的面积为S,试求S的最大值;
(3)如图2, 连结PM、AM, 试探究: 在点 P、M运动的过程中,是否存在某个时刻,使得△PMB 为直角三角形且△PMA 是等腰三角形 若存在,求出此时a和t的取值,若不存在,请说明理由.
19. 如图, 在矩形ABCD中, AB=3, BC=4. 动点 P从点A 出发沿AC 向终点C运动,同时动点Q 从点 B 出发沿BA向点A 运动,到达A 点后立刻以原来的速度沿AB返回. 点P,Q运动速度均为每秒 1个单位长度,当点 P到达点 C时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
(1) 求线段AC的长度;
(2)当点Q从B点向A点运动时(未到达A点),求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线为l:①当l经过点 A 时, 射线 QP交AD 于点 E, 求AE的长;
②当l经过点B时,求t的值.
20. 如图1,已知矩形ABCD中,AB=60cm, BC=90cm. 点P 从点A 出发, 以3cm/s 的速度沿AB运动: 同时, 点Q从点 B 出发, 以 20cm/s 的速度沿 BC运动. 当点 Q 到达点 C时,P、Q两点同时停止运动.设点 P、Q运动的时间为t(s).
(1) 当t= s时, △BPQ为等腰三角形;
(2) 当BD平分 PQ时, 求t的值;
(3)如图2, 将△BPQ 沿 PQ 折叠, 点 B 的对应点为 E,PE、QE分别与AD交于点F、G.
探索:是否存在实数t,使得AF=EF 如果存在,求出t的值:如果不存在,说明理由.
第4讲 动态问题分析
1.B.
解析: x=2时, 快车慢车相遇, 当2
2. ②④.
解析: 点 G: B点到了 C点; 点 M: P 点到了点 E; 点 N:P点到了点D;
可求AD=BE=10, 故结论①错误;
过点 P 作 PH⊥BC 交 BC 于点 H, 当当0
当 时, 此时
∴△ABE∽△QBP, 故结论④正确;
结论⑤显然错误.
综上所述,正确的是②④.
3.C.
4.A.
解析: 当0
(2) 过点 D 作 DM⊥AB, 则 AM=3, DM=4, ∴AD=5,
在△AP H 中,
∴P B=1, 连接P P , 则P P ∥AD,∴BP =
故 的值为
6..解析:(1) 由题意得, 当6≤t≤8时, 点P从C向D运动, 故CD=2×2=4,
当t=6时, 点P与点C重合,
故矩形ABCD的长为8, 宽为4.
(2)a秒时, 点P在BC中点处,
从a秒至6秒,点P运动了4秒,又点P速度为2个单位每秒,故a的值为4,
m=4÷4=1, b秒时, 点P距离A点2个单位, 故b=8+6+2=8+3=11,
故m的值为1; a的值为4; b的值为11.
7.解析: (1) 考虑当时间为a时, △APD面积为24,可得 a=8, 考虑接下来2秒运动了4cm, ∴b=2,对于点 C来说,整个运动过程时间为22s,
即2×8+c·(22-8)=30, ∴c=1,
综上, a=8, b=2, c=1;
(2) 当0
当P、Q相遇时, 即8+8×2+3(x-8)=30, 解得: x=10,故10秒时, 点 P、Q相遇.
8.解析: (1) 点A坐标为(6, 3), 点D坐标为(0, 3);
(2)点F:Q到点 C,P到点.A,
(3)①当0
若PQ=CQ, 过点 P 作 PH⊥BC交 BC 于点 H, 则 PH=3,HQ=|9-5t|, 则. 又CQ=6-2t,
整理得: ,∴方程无实根;
若 即 整理得:
解得: (舍),
③当3
综上所述,当t的值为 或15/4时, △PCQ是等腰三角形.
9.解析: (1) 当x=m时, 点Q到了点 C, 故
(2)当0
当 时,
综上,
(3)当0
即 解得:
当 时, CP=CQ, 即 解得:
综上所述,当△PCQ 为等腰三角形时,x的值为 或
10. 解析: (1) 由图像可知当 x=1 时, 点 F 到达点 C, 故BC=3cm,
当x=2时, 点F到点D, ∴CD=3cm, ∴AB=3cm,x=1时,△BEF的面积为 又此时BF=3cm,∴BE=1cm,故点E的速度为1cm/s;
(2)当0
(3) 当点F在BC上时, 易证△EBF∽△FCD,
当点F在 CD上时, 若CF=BE, 则∠EFD=90°,即3x-3=x, 解得:
综上, 当∠DFE=90°时, x的值为 或
11.解析: (1) 连接AD, 则AD=x, ∵MA=MD,
∴△AMQ是等边三角形,
即
当x=2时,重叠部分面积取到最大值,最大值是
12. 解析:(1)由函数图像可得AC=2,∴AO=2,∴k=- 当点D落在x轴上,此时平移的距离为4,∴a=4;
(2)当0
13. 解析: (1) 当t=2 时, GF 边与 BC 边重合, 过点 A 作AH⊥DE交DE于点H, 则△AHD∽△DGB,
易证△ADE∽△ABC, ∴DEC=ADB= , ∴BC=6.
(2)t=2时, 故a的值为
(3)当0
14. 解析: (1) AP=2x(cm).
(2) 当点D落在BC上时, 易证△PDB≌△QPA,
∴BP=AQ=2AP, 即
(3)当 时,
当 时,
当1
15. 解析:(1)∵点C坐标为(3,4),∴OC=5,∴CB=OC=5,∴点B坐标为(8, 4).
(2)当M、N分别为OA、OC中点或M、N分别为AB、CB中点时,
当M为OA中点时,
当N为CB中点时,
综上,当 时,t的值为 或
(3)当0
当5
由题意可得: AM=AD=t-5,
综上,
当t=5时, S取到最大值10.
16.解析: (1) 点C坐标为(-3,4), 点B 坐标为(1,7);
(2) 当t=2时, CP=2, 且CP≠PQ,
当CP=CQ时, CQ=2, 点Q 的路程为5+3=8, 故k=4;当CQ=PQ时,点Q在CP的垂直平分线上,OQ=1,则AQ=4,∴k=2.
综上所述,k的值为4或2.
(3)当0
17解析:(1) EF=AE=t;
点F坐标为
解得:
∴当t的值为 时,点H与点C重合.
(3) ①当 时,
②当 时,
③当5
(4) 如图, △AFH即为扫过的面积, 故运动过程中,△EFH扫过的面积为
18.解析: (1) 5-at;
(2) 过点P作PH⊥OB交OB于点H, 则
当t=2时,S取到最大值
(3) 若∠PMB=90°且PM=PA,
此时 即 解得:
若∠BPM=90°且PM=PA,则
此时 即 解得: 综上,
19.解析: (1) AC=5;
(2)过点P作PG⊥AB交AB于点H,则
又AQ=AB-BQ=3-t,
(3)①直线l经过点A, 即AQ=AP,
情况1: 当0
过点Q作QO∥AD, 易证点O为AC中点, ∴OP=1,
易证∠△APE∽△OPQ,∴AEO=AP= 又 ∴AE=3
情况2: 当3≤t<5时, AP≠AQ.
综上,直线l过点A时,AE的值为3.
②当直线l经过点B时, 连接BP, 则BQ=BP,
情况1: 当0
解得: 综上,t的值为 或.
20. 解析: (1) 若△BPQ为等腰三角形, 则BP=BQ,
由题意得: BP=60-3t, BQ=20t,
∴60-3t=20t, 解得:
故 时,△BPQ为等腰三角形;
(2)若BD平分 PQ,则 即 解得: 故当BD平分PQ时,t的值为
(3) 若AF=EF, 则△AFP∽△EFG, 可得AG=EP,
由题意得: AP=3t, AG=PE=PB=60-3t,
DG=90-(60-3t)=3t+30,
GQ=EQ-EG=20t-3t=17t,过点Q作QH⊥AD交AD于点 H,
则GH=3t+30-(90-20t)=23t-60,
又
代入得: 解得: (舍)
故当t=4时, AF=EF.
同课章节目录
