2025年中考数学压轴题二轮专题复习讲练第1讲 常见相似模型(含解析)
文档属性
| 名称 | 2025年中考数学压轴题二轮专题复习讲练第1讲 常见相似模型(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 516.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览




文档简介
第1讲 常见相似模型
前言:相似三角形是初中几何的重难点,形式众多、变化多样是其难点,也是复习的重点,本讲介绍一些常见的相似图形及考察方式.
中小学教育资源及组卷应用平台
知 识 导 航
A字型与8字型
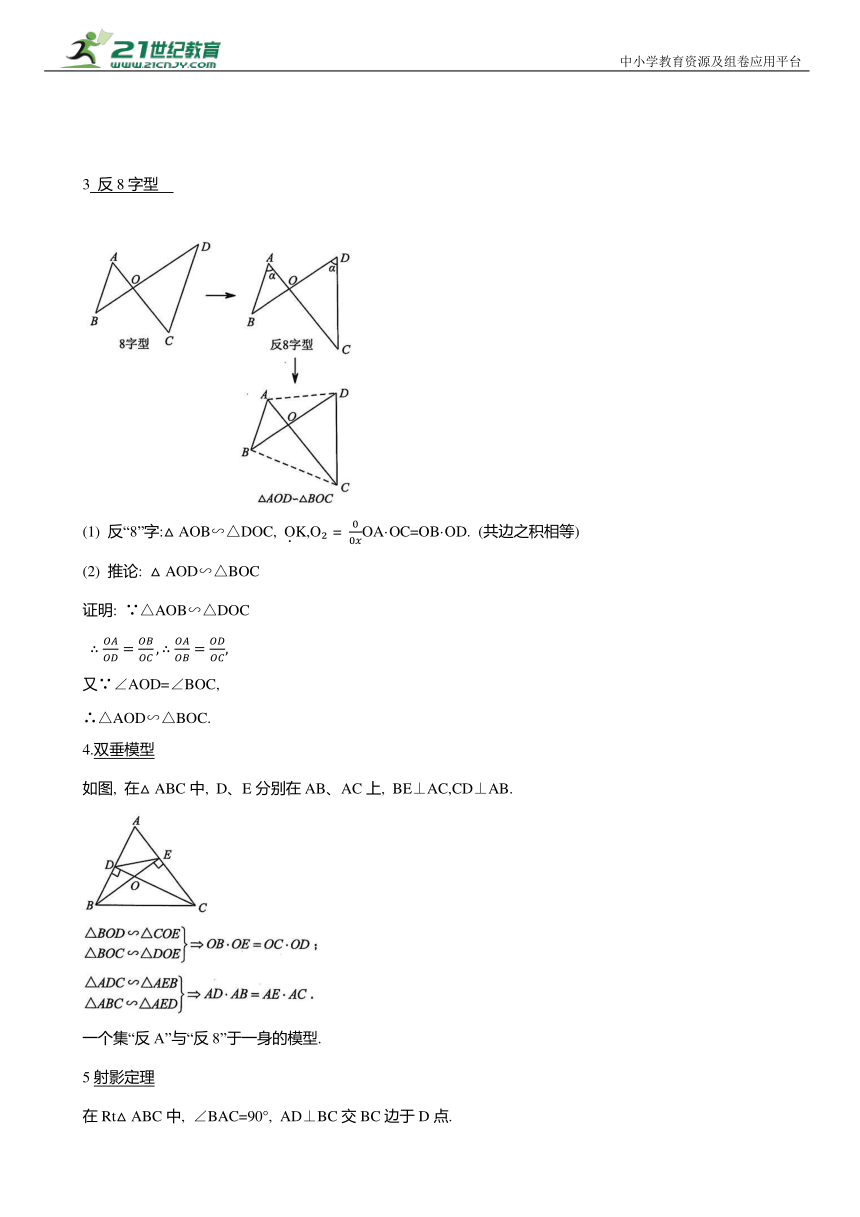
(1) “A”字型
在△ABC中, 若DE∥BC, 则△ADE∽△ABC,
(2) “8”字型
若ED∥BC,则
引例1:如图,在平行四边形ABCD中, ∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G, 若AF=2FD, 则 的值为( )
A. B. C. D.
解析: 若AF=2FD, 则 选C.
2 反A字型
(1)反“A”字: AD·AB=AE·AC . (共边之积相等)
(2) 母子型: (平方式,找母子)
(3) 推论: △ADC∽△AEB.
且∠DAC=∠EAB.)
引例2: 如图, D 是△ABC的边 BC 上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD 的面积为 ( )
A. 15 B. 10 C. D. 5
解析: ∵∠DAC=∠B, ∴△CDA∽△CAB,
∴选D.
引例3: (2018·常州) 如图, 在△ABC纸板中, AC=4,BC=2,AB=5,P是AC上一点, 过点 P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是 .
解析:如图,其中有三组始终存在:
△CPQ∽△CAB, △APQ∽△ACB, △APQ∽△ABC.
若△CPQ∽△CBA, 则 当点Q与B重合时,AP 取到最小值, 代入得 CP=1, 此时 AP=3,∴AP的取值范围是3≤AP<4.
3 反8字型
(1) 反“8”字:△AOB∽△DOC, OK,O = OA·OC=OB·OD. (共边之积相等)
(2) 推论: △AOD∽△BOC
证明: ∵△AOB∽△DOC
又∵∠AOD=∠BOC,
∴△AOD∽△BOC.
4.双垂模型
如图, 在△ABC中, D、E分别在AB、AC上, BE⊥AC,CD⊥AB.
一个集“反A”与“反8”于一身的模型.
5射影定理
在Rt△ABC中, ∠BAC=90°, AD⊥BC交BC边于D点.
引例4: 如图, AB是⊙O的直径, AM和BN是它的两条切线,过⊙O上一点 E作直线DC,分别交 AM、BN于点D、C, 且DA=DE.
(1) 求证: 直线CD是⊙O的切线;
(2) 求证:
解析: (1) 连接OE、OD, 在△OAD和△OED中,
∴∠OED=∠OAD, ∵AM是⊙O的切线,
∴∠OAD=90°, ∴∠OED=90°,
∴CD是⊙O的切线.
连接OC, 在 Rt△OBC和Rt△OEC中,
∴△OBC≌△OEC(HL),
∴∠BOC=∠EOC, 又△OAD≌△OED, ∴∠AOD=∠EOD,
在 Rt△DOC中,由射影定理可得:
6. 三角形内接正方形
如图, 在△ABC中, E、F分别是AB、AC上的点, 且四边形DEFG是正方形.
结论: (d为内接正方形边长)
证明:
引例5: 如图, 已知正方形 DEFG的顶点 D、E在△ABC的边BC上, 顶点 G、F分别在边AB、AC上. 如果 BC=4,△ABC 的面积是 6,那么这个正方形的边长是
解析: 过点A作AH⊥BC交BC于点H,
则 解得: AH=3.
正方形边长为
7 三平行模型
如图, AB∥CD∥EF, 记AB=a, CD=b, EF=c.
结论:
证明:
8黄金分割
(1) 黄金分割点: 如图, 点C 在线段 AB 上, 若满足 则点C称为线段AB的黄金分割点.
(2) 黄金分割比:
(3) 黄金三角形
引例 6: 如图, 在△ABC 中, AB=AC=1, 在AC边上截取AD=BC, 连接BD.
(1) 通过计算, 判断AD 与AC·CD的大小关系;
(2) 求∠ABD的度数.
解析:
又∠BCD=∠ACB, ∴△BCD∽△ACB,
∴∠BDC=∠ABC=∠ACB, ∠CBD=∠BAC,
∴BD=BC=AD, 设∠C=α, 则∠ABC=∠BDC=α,
∠A+∠ABD=α, ∴∠A=α/ ,
即∠ABD的度数是36°.
(4) 黄金分割与正方形
如图, 在正方形 ABCD 中, E是 AD 边中点, F在 AB 边上且CF平分∠BCE,则点 F是线段AB 的黄金分割点.
证明:延长CF交DA 延长线于 G点,
则∠G=∠BCF=∠ECF, ∴EG=EC,
设边长AD=2m, 则AE=DE=m, EG=EC= m,
∴AG=( -1)m, ∵△AFG∽△BFC,
即
∴点F是线段AB 的黄金分割点.
引例7:如图, 在正方形纸片ABCD中, E是CD 的中点,将正方形纸片折叠,点B 落在线段 AE 上的点G处, 折痕为AF. 若AD=4, 则 CF的长为 .
解析:
∵BC=AD=4, ∴CF=6-2
(本题在第3章第1节出现过,另可用勾股定理求解.)
真 题 演 练
1. 如图, 在△ABC中, D是AB上的一点,∠ACD=∠B, AC=2, AB=4, 则AD= .
2. 如图, BC∥DE, 且BC3. 如图, 矩形ABCD中, AB=4, AD=3, 点Q在对角线AC上, 且AQ=AD, 连接DQ 并延长, 与边 BC交于点 P, 则线段AP= .
4. 如图,在△ABC中, 点D在BC边上,连接AD, 点E在AC边上, 过点 E作EF∥BC, 交AD于点F, 过点E作EG∥AB,交BC于点 G, 则下列式子一定正确的是( )
5. 如图, 在Rt△ABC中, ∠ACB=90°,AC=3, BC=4, CD⊥AB, 垂足为D, E为BC的中点, AE与 CD交于点F, 则DF的长为 .
6.如图,点E、F分别在菱形ABCD的边AB、AD上,且AE=DF, BF交DE于点G, 延长BF交CD的延长线于H,若 则 的值为 ( )
A. B. C. D.
7.如图, 在矩形ABCD中, E、F分别为边AB、AD的中点, BF与EC、ED分别交于点 M, N. 已知AB=4, BC=6, 则MN的长为 .
8.如图,在Rt△ABC中,∠ACB=90°,AB=4,点D、E分别在边AB、AC上, 且DB=2AD, AE=3EC, 连接BE、CD, 相交于点O, 则△ABO面积最大值为 .
9. 在Rt△ABC中, ∠C=90°, AD平分∠CAB, BE平分∠ABC, AD、BE相交于点F, 且AF=4, 则AC= .
10. 如图, 矩形ABCD中, E 为边 AB上一点, 将△ADE 沿 DE 折叠, 使点 A 的对应点 F 恰好落在边BC上, 连接AF交 DE于点 N, 连接 BN. 若BF·AD=15, 则矩形ABCD的面积为 .
11. 如图, 在△ABC中, 点D、E分别在边AB、AC上, ∠AED=∠B, 射线AG分别交线段DE、BC于点F、G,且
(1) 求证: △ADF∽△ACG;
(2) 若 求 的值.
12. 如图1,四边形ABCD的对角线AC、BD相交于点O, OA=OC, OB=OD+CD.
(1) 过A作AE∥DC交BD于点E, 求证: AE=BE;
(2) 图2, 将△ABD沿AB翻折得到△ABD'.
①求证: BD'∥CD;
②若AD'∥BC, 求证:(
13.【初步尝试】
(1)如图1,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 ;
【思考说理】
(2)如图2,在三角形纸片ABC中,AC=BC=6,AB=10,将△ABC折叠,使点B与点C重合,折痕为MN,求 的值;
【拓展延伸】
(3) 如图3, 在三角形纸片ABC中, AB=9, BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B'处,折痕为CM.
①求线段AC的长;
②若点 O 是边 AC 的中点,点P 为线段 OB'上的一个动点,将△APM沿 PM 折叠得到△A'PM, 点A 的对应点为点 A',A'M与CP交于点 F, 求 的取值范围.
14.小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1) 温故如图 1, 在△ABC 中, AD⊥BC 于点 D, 正方形PQMN的边QM在BC上, 顶点 P、N分别在AB、AC上,若BC=a, AD=h,求正方形 PQMN的边长(用a、h表示).
(2) 操作:如何画出这个正方形 PQMN呢
如图2,小波画出了图1的△ABC,然后按数学家波利亚在《怎样解题》中的方法进行操作:先在AB上任取一点 P',画正方形P'Q'M'N',使点Q'、M'在BC边上, 点N'在△ABC内, 然后连结 BN', 并延长交AC于点 N,画NM⊥BC于点 M,NP⊥NM交AB于点 P,PQ⊥BC于点 Q, 得到四边形 PQMN.
(3) 推理:证明图2中的四边形 PQMN 是正方形.
(4)拓展:小波把图2中的线段BN称为“波利亚线”,在该线上截取 NE=NM, 连结 EQ、EM (如图 3), 当∠QEM=90°时, 求“波利亚线” BN 的长(用 a, h 表示).
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
15. 我们知道: 如图①, 点B把线段AC分成两部分,如果 那么称点B为线段AC的黄金分割点. 它们的比值为
(1) 在图①中, 若AC=20cm, 则AB的长为 cm;
(2) 如图②,用边长为 20cm的正方形纸片进行如下操作:对折正方形 ABCD 得折痕 EF, 连接 CE, 将 CB 折叠到 CE上, 点 B对应点H, 得折痕CG. 试说明: G是AB 的黄金分割点;
(3)如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作 CF⊥BE,交AB 于点F,延长EF、CB 交于点 P. 他发现当PB与BC满足某种关系时,E、F恰好分别是 AD、AB的黄金分割点. 请猜想小明的发现,并说明理由.
第1讲 常见相似模型
1.解析: 由题意可得△ADC∽△ACB,∴AC =AD·AB, 代入得AD=1.
2.解析: 设 AB=x, 则 DE=10-x, 易证△ABC∽△ADE, ∴ 代入得: 解得:x =2,x =8(舍), 的值为2.
3.解析: ∵AD=3, CD=4, ∴AC=5, ∵AQ=AD=3, ∴CQ=2,易证△ADQ∽△CPQ,∴CP=CQ=2,∴BP=1, .
4.解析: ∴选C.
5. 解析:过点F作FH⊥AC交AC于点H,设FH=x,则 易证△AHF∽△ACE,∴FHCE=AHC,代入得: 解得: 又 ∴DF 的长为
6. B.
解析: 即 ∴ 即 故选B.
7.
解析: ∵AD=BC=6, F是AD边中点, ∴AF=3, 又AB=4,
∴BF=5,延长CE与DA延长线交于点P,则△AEP≌△BEC,∴AP=BC=6, 易证 代入得: 延长BF与CD延长线交于点 Q, 则△FDQ≌△FAB,∴DQ=AB=4, 易证 故MN的长为
8.
解析: 过点D作DF∥AC交BE于点F, 又 即
弧,当△ABC是等腰直角三角形时,面积最大,△ABC面积最大值是4,∴△ABO面积最大值是
9.解析: 在 Rt△ABC中, ∠BAC+∠ABC=90°,
即∠BAF+∠ABF=∠AFE=45°,连接CF,则CF平分∠ACB,∴∠ACF=45°, ∴△AEF∽△AFC, ∴AF =AE·AC.
过点E作EH⊥AD交AD于点H,则△EHF是等腰直角三角形,∵EF= , ∴EH=FH=1, AH=3, ∴AE=
即
10.15
解析: ∵DA=DF, ∴∠DAF=∠DFA, 又∠DAF=∠AFB,易证△DAF∽△NBF,∴∠ADF=∠BNF,∴tan∠ADF= 设CF=2a,则DC= a,∴DF=DA=3a,∴BF=a, AF= a, ∵△DAF∽△NBF, ∴BF=NB/AD, 解得: ∴矩形ABCD面积为
11. 解析: (1) ∵∠AED=∠B, ∠DAE=∠CAB,
∴△DAE∽△CAB, ∴∠ADE=∠ACB, 又
∴△ADF∽△ACG.
即 的值为1.
12. 解析: (1) ∵AE∥DC, ∴∠OAE=∠OCD,∠OEA=∠ODC,又OA=OC,∴△OAE≌△OCD,∴AE=CD,OE=OD, ∵OB=OD+CD, ∴OB=OE+AE, ∴AE=BE.
(2)①过点A作AM∥CD交BD于点 M,由(1)得AM=BM,∴∠BAM=∠ABM,又∠ABM=∠ABD', ∴∠BAM=∠ABD',∴BD'∥AM, ∴BD'∥CD.
②连接CM,则四边形AMCD 是平行四边形,
∴∠CMD=∠ADM,
∵AD'∥BC, ∴∠D'+∠D'BC=180°, ∵D'B ∥DC,
∴∠D'BC+∠BCD=180°, ∴∠D'=∠BCD,
∴∠CMD=∠ADM=∠D'=∠BCD, ∴△DCM∽△DBC,
即 又DM=2OD,
13.解析: (1) AM=BM;
(2) 过点C作CH⊥AB交AB于点H, 则AH=BH=5,
将BN=3代入得:
(3) ①∵∠ACB=2∠A, 且CM平分∠ACB,
∴∠BCM=∠A, ∴△BCM∽△BAC,
∴BC =BM·BA,∴BM=4,CM=AM=5,∵CMC=BMC= 即线段AC的长为
②∵∠A'=∠A=∠ACM , ∴△A'FP∽△CFM,
当点P与点B'重合时, 此时A'P=AP 取到最小值 , 取到最小值 , 当点P与点O重合时, 此时A'P=AP 取到最大值 , PCM:取到最大值
的取值范围是
14. 解析:(1)易证△APN≌△ABC,∴PNC=AHAD,设正方形 PQMN边长为x, 则 解得:
(3) 已知四边形 PQMN是矩形,故只需再证明有一组邻边相等即可.
易证△BM'N'∽△BMN, ∴M'N'=BN'N',
易证△BP'N'∽△BPN, ∴PNN=BN,
又M'N'=P'N', ∴MN=PN.
∴四边形PQMN是正方形.
(4) ∵NE=NM, ∴∠NEM=∠NME,
∵∠QEM=90°, ∴∠NEM+∠BEQ=90°,
又∵∠NME+∠BME=90°, ∴∠BEQ=∠BME,
∴△BQE∽△BEM,
设BQ=m, 则
在 Rt△BNM中,
代入得: 解得:
15. 解析:(1)∵点B是AC的黄金分割点,
(2) 连接 EG, 设 BG=x, 则 GH=x, AG=(20-x) cm,
代入得:
解得:
即BG的长为
∴点G是AB的黄金分割点.
(3)∵CF⊥BE,易证△CBF≌△BAE,∴BF=AE,AF=DE,∵点E是AD的黄金分割点, 且AE>DE,
∴当PB=BC时, E、F 恰好分别是 AD、AB 的黄金分割点.
前言:相似三角形是初中几何的重难点,形式众多、变化多样是其难点,也是复习的重点,本讲介绍一些常见的相似图形及考察方式.
中小学教育资源及组卷应用平台
知 识 导 航
A字型与8字型
(1) “A”字型
在△ABC中, 若DE∥BC, 则△ADE∽△ABC,
(2) “8”字型
若ED∥BC,则
引例1:如图,在平行四边形ABCD中, ∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G, 若AF=2FD, 则 的值为( )
A. B. C. D.
解析: 若AF=2FD, 则 选C.
2 反A字型
(1)反“A”字: AD·AB=AE·AC . (共边之积相等)
(2) 母子型: (平方式,找母子)
(3) 推论: △ADC∽△AEB.
且∠DAC=∠EAB.)
引例2: 如图, D 是△ABC的边 BC 上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD 的面积为 ( )
A. 15 B. 10 C. D. 5
解析: ∵∠DAC=∠B, ∴△CDA∽△CAB,
∴选D.
引例3: (2018·常州) 如图, 在△ABC纸板中, AC=4,BC=2,AB=5,P是AC上一点, 过点 P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是 .
解析:如图,其中有三组始终存在:
△CPQ∽△CAB, △APQ∽△ACB, △APQ∽△ABC.
若△CPQ∽△CBA, 则 当点Q与B重合时,AP 取到最小值, 代入得 CP=1, 此时 AP=3,∴AP的取值范围是3≤AP<4.
3 反8字型
(1) 反“8”字:△AOB∽△DOC, OK,O = OA·OC=OB·OD. (共边之积相等)
(2) 推论: △AOD∽△BOC
证明: ∵△AOB∽△DOC
又∵∠AOD=∠BOC,
∴△AOD∽△BOC.
4.双垂模型
如图, 在△ABC中, D、E分别在AB、AC上, BE⊥AC,CD⊥AB.
一个集“反A”与“反8”于一身的模型.
5射影定理
在Rt△ABC中, ∠BAC=90°, AD⊥BC交BC边于D点.
引例4: 如图, AB是⊙O的直径, AM和BN是它的两条切线,过⊙O上一点 E作直线DC,分别交 AM、BN于点D、C, 且DA=DE.
(1) 求证: 直线CD是⊙O的切线;
(2) 求证:
解析: (1) 连接OE、OD, 在△OAD和△OED中,
∴∠OED=∠OAD, ∵AM是⊙O的切线,
∴∠OAD=90°, ∴∠OED=90°,
∴CD是⊙O的切线.
连接OC, 在 Rt△OBC和Rt△OEC中,
∴△OBC≌△OEC(HL),
∴∠BOC=∠EOC, 又△OAD≌△OED, ∴∠AOD=∠EOD,
在 Rt△DOC中,由射影定理可得:
6. 三角形内接正方形
如图, 在△ABC中, E、F分别是AB、AC上的点, 且四边形DEFG是正方形.
结论: (d为内接正方形边长)
证明:
引例5: 如图, 已知正方形 DEFG的顶点 D、E在△ABC的边BC上, 顶点 G、F分别在边AB、AC上. 如果 BC=4,△ABC 的面积是 6,那么这个正方形的边长是
解析: 过点A作AH⊥BC交BC于点H,
则 解得: AH=3.
正方形边长为
7 三平行模型
如图, AB∥CD∥EF, 记AB=a, CD=b, EF=c.
结论:
证明:
8黄金分割
(1) 黄金分割点: 如图, 点C 在线段 AB 上, 若满足 则点C称为线段AB的黄金分割点.
(2) 黄金分割比:
(3) 黄金三角形
引例 6: 如图, 在△ABC 中, AB=AC=1, 在AC边上截取AD=BC, 连接BD.
(1) 通过计算, 判断AD 与AC·CD的大小关系;
(2) 求∠ABD的度数.
解析:
又∠BCD=∠ACB, ∴△BCD∽△ACB,
∴∠BDC=∠ABC=∠ACB, ∠CBD=∠BAC,
∴BD=BC=AD, 设∠C=α, 则∠ABC=∠BDC=α,
∠A+∠ABD=α, ∴∠A=α/ ,
即∠ABD的度数是36°.
(4) 黄金分割与正方形
如图, 在正方形 ABCD 中, E是 AD 边中点, F在 AB 边上且CF平分∠BCE,则点 F是线段AB 的黄金分割点.
证明:延长CF交DA 延长线于 G点,
则∠G=∠BCF=∠ECF, ∴EG=EC,
设边长AD=2m, 则AE=DE=m, EG=EC= m,
∴AG=( -1)m, ∵△AFG∽△BFC,
即
∴点F是线段AB 的黄金分割点.
引例7:如图, 在正方形纸片ABCD中, E是CD 的中点,将正方形纸片折叠,点B 落在线段 AE 上的点G处, 折痕为AF. 若AD=4, 则 CF的长为 .
解析:
∵BC=AD=4, ∴CF=6-2
(本题在第3章第1节出现过,另可用勾股定理求解.)
真 题 演 练
1. 如图, 在△ABC中, D是AB上的一点,∠ACD=∠B, AC=2, AB=4, 则AD= .
2. 如图, BC∥DE, 且BC
4. 如图,在△ABC中, 点D在BC边上,连接AD, 点E在AC边上, 过点 E作EF∥BC, 交AD于点F, 过点E作EG∥AB,交BC于点 G, 则下列式子一定正确的是( )
5. 如图, 在Rt△ABC中, ∠ACB=90°,AC=3, BC=4, CD⊥AB, 垂足为D, E为BC的中点, AE与 CD交于点F, 则DF的长为 .
6.如图,点E、F分别在菱形ABCD的边AB、AD上,且AE=DF, BF交DE于点G, 延长BF交CD的延长线于H,若 则 的值为 ( )
A. B. C. D.
7.如图, 在矩形ABCD中, E、F分别为边AB、AD的中点, BF与EC、ED分别交于点 M, N. 已知AB=4, BC=6, 则MN的长为 .
8.如图,在Rt△ABC中,∠ACB=90°,AB=4,点D、E分别在边AB、AC上, 且DB=2AD, AE=3EC, 连接BE、CD, 相交于点O, 则△ABO面积最大值为 .
9. 在Rt△ABC中, ∠C=90°, AD平分∠CAB, BE平分∠ABC, AD、BE相交于点F, 且AF=4, 则AC= .
10. 如图, 矩形ABCD中, E 为边 AB上一点, 将△ADE 沿 DE 折叠, 使点 A 的对应点 F 恰好落在边BC上, 连接AF交 DE于点 N, 连接 BN. 若BF·AD=15, 则矩形ABCD的面积为 .
11. 如图, 在△ABC中, 点D、E分别在边AB、AC上, ∠AED=∠B, 射线AG分别交线段DE、BC于点F、G,且
(1) 求证: △ADF∽△ACG;
(2) 若 求 的值.
12. 如图1,四边形ABCD的对角线AC、BD相交于点O, OA=OC, OB=OD+CD.
(1) 过A作AE∥DC交BD于点E, 求证: AE=BE;
(2) 图2, 将△ABD沿AB翻折得到△ABD'.
①求证: BD'∥CD;
②若AD'∥BC, 求证:(
13.【初步尝试】
(1)如图1,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 ;
【思考说理】
(2)如图2,在三角形纸片ABC中,AC=BC=6,AB=10,将△ABC折叠,使点B与点C重合,折痕为MN,求 的值;
【拓展延伸】
(3) 如图3, 在三角形纸片ABC中, AB=9, BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B'处,折痕为CM.
①求线段AC的长;
②若点 O 是边 AC 的中点,点P 为线段 OB'上的一个动点,将△APM沿 PM 折叠得到△A'PM, 点A 的对应点为点 A',A'M与CP交于点 F, 求 的取值范围.
14.小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1) 温故如图 1, 在△ABC 中, AD⊥BC 于点 D, 正方形PQMN的边QM在BC上, 顶点 P、N分别在AB、AC上,若BC=a, AD=h,求正方形 PQMN的边长(用a、h表示).
(2) 操作:如何画出这个正方形 PQMN呢
如图2,小波画出了图1的△ABC,然后按数学家波利亚在《怎样解题》中的方法进行操作:先在AB上任取一点 P',画正方形P'Q'M'N',使点Q'、M'在BC边上, 点N'在△ABC内, 然后连结 BN', 并延长交AC于点 N,画NM⊥BC于点 M,NP⊥NM交AB于点 P,PQ⊥BC于点 Q, 得到四边形 PQMN.
(3) 推理:证明图2中的四边形 PQMN 是正方形.
(4)拓展:小波把图2中的线段BN称为“波利亚线”,在该线上截取 NE=NM, 连结 EQ、EM (如图 3), 当∠QEM=90°时, 求“波利亚线” BN 的长(用 a, h 表示).
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
15. 我们知道: 如图①, 点B把线段AC分成两部分,如果 那么称点B为线段AC的黄金分割点. 它们的比值为
(1) 在图①中, 若AC=20cm, 则AB的长为 cm;
(2) 如图②,用边长为 20cm的正方形纸片进行如下操作:对折正方形 ABCD 得折痕 EF, 连接 CE, 将 CB 折叠到 CE上, 点 B对应点H, 得折痕CG. 试说明: G是AB 的黄金分割点;
(3)如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作 CF⊥BE,交AB 于点F,延长EF、CB 交于点 P. 他发现当PB与BC满足某种关系时,E、F恰好分别是 AD、AB的黄金分割点. 请猜想小明的发现,并说明理由.
第1讲 常见相似模型
1.解析: 由题意可得△ADC∽△ACB,∴AC =AD·AB, 代入得AD=1.
2.解析: 设 AB=x, 则 DE=10-x, 易证△ABC∽△ADE, ∴ 代入得: 解得:x =2,x =8(舍), 的值为2.
3.解析: ∵AD=3, CD=4, ∴AC=5, ∵AQ=AD=3, ∴CQ=2,易证△ADQ∽△CPQ,∴CP=CQ=2,∴BP=1, .
4.解析: ∴选C.
5. 解析:过点F作FH⊥AC交AC于点H,设FH=x,则 易证△AHF∽△ACE,∴FHCE=AHC,代入得: 解得: 又 ∴DF 的长为
6. B.
解析: 即 ∴ 即 故选B.
7.
解析: ∵AD=BC=6, F是AD边中点, ∴AF=3, 又AB=4,
∴BF=5,延长CE与DA延长线交于点P,则△AEP≌△BEC,∴AP=BC=6, 易证 代入得: 延长BF与CD延长线交于点 Q, 则△FDQ≌△FAB,∴DQ=AB=4, 易证 故MN的长为
8.
解析: 过点D作DF∥AC交BE于点F, 又 即
弧,当△ABC是等腰直角三角形时,面积最大,△ABC面积最大值是4,∴△ABO面积最大值是
9.解析: 在 Rt△ABC中, ∠BAC+∠ABC=90°,
即∠BAF+∠ABF=∠AFE=45°,连接CF,则CF平分∠ACB,∴∠ACF=45°, ∴△AEF∽△AFC, ∴AF =AE·AC.
过点E作EH⊥AD交AD于点H,则△EHF是等腰直角三角形,∵EF= , ∴EH=FH=1, AH=3, ∴AE=
即
10.15
解析: ∵DA=DF, ∴∠DAF=∠DFA, 又∠DAF=∠AFB,易证△DAF∽△NBF,∴∠ADF=∠BNF,∴tan∠ADF= 设CF=2a,则DC= a,∴DF=DA=3a,∴BF=a, AF= a, ∵△DAF∽△NBF, ∴BF=NB/AD, 解得: ∴矩形ABCD面积为
11. 解析: (1) ∵∠AED=∠B, ∠DAE=∠CAB,
∴△DAE∽△CAB, ∴∠ADE=∠ACB, 又
∴△ADF∽△ACG.
即 的值为1.
12. 解析: (1) ∵AE∥DC, ∴∠OAE=∠OCD,∠OEA=∠ODC,又OA=OC,∴△OAE≌△OCD,∴AE=CD,OE=OD, ∵OB=OD+CD, ∴OB=OE+AE, ∴AE=BE.
(2)①过点A作AM∥CD交BD于点 M,由(1)得AM=BM,∴∠BAM=∠ABM,又∠ABM=∠ABD', ∴∠BAM=∠ABD',∴BD'∥AM, ∴BD'∥CD.
②连接CM,则四边形AMCD 是平行四边形,
∴∠CMD=∠ADM,
∵AD'∥BC, ∴∠D'+∠D'BC=180°, ∵D'B ∥DC,
∴∠D'BC+∠BCD=180°, ∴∠D'=∠BCD,
∴∠CMD=∠ADM=∠D'=∠BCD, ∴△DCM∽△DBC,
即 又DM=2OD,
13.解析: (1) AM=BM;
(2) 过点C作CH⊥AB交AB于点H, 则AH=BH=5,
将BN=3代入得:
(3) ①∵∠ACB=2∠A, 且CM平分∠ACB,
∴∠BCM=∠A, ∴△BCM∽△BAC,
∴BC =BM·BA,∴BM=4,CM=AM=5,∵CMC=BMC= 即线段AC的长为
②∵∠A'=∠A=∠ACM , ∴△A'FP∽△CFM,
当点P与点B'重合时, 此时A'P=AP 取到最小值 , 取到最小值 , 当点P与点O重合时, 此时A'P=AP 取到最大值 , PCM:取到最大值
的取值范围是
14. 解析:(1)易证△APN≌△ABC,∴PNC=AHAD,设正方形 PQMN边长为x, 则 解得:
(3) 已知四边形 PQMN是矩形,故只需再证明有一组邻边相等即可.
易证△BM'N'∽△BMN, ∴M'N'=BN'N',
易证△BP'N'∽△BPN, ∴PNN=BN,
又M'N'=P'N', ∴MN=PN.
∴四边形PQMN是正方形.
(4) ∵NE=NM, ∴∠NEM=∠NME,
∵∠QEM=90°, ∴∠NEM+∠BEQ=90°,
又∵∠NME+∠BME=90°, ∴∠BEQ=∠BME,
∴△BQE∽△BEM,
设BQ=m, 则
在 Rt△BNM中,
代入得: 解得:
15. 解析:(1)∵点B是AC的黄金分割点,
(2) 连接 EG, 设 BG=x, 则 GH=x, AG=(20-x) cm,
代入得:
解得:
即BG的长为
∴点G是AB的黄金分割点.
(3)∵CF⊥BE,易证△CBF≌△BAE,∴BF=AE,AF=DE,∵点E是AD的黄金分割点, 且AE>DE,
∴当PB=BC时, E、F 恰好分别是 AD、AB 的黄金分割点.
同课章节目录
