2025年中考数学压轴题二轮专题复习讲练 第5章 特殊图形存在性问题第5节 菱形存在性问题(含解析)
文档属性
| 名称 | 2025年中考数学压轴题二轮专题复习讲练 第5章 特殊图形存在性问题第5节 菱形存在性问题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 294.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览



文档简介
第5节 菱形存在性问题
前言:与矩形相似,菱形存在性问题也可从两个角度来考虑,即从等腰到菱形或从平四到菱形,具体方法选择还需具体问题具体分析.
中小学教育资源及组卷应用平台
知 识 导 航
问题探究
先从菱形的判定着手考虑:
判定1:有一组邻边相等的平行四边形菱形;
判定2:对角线互相垂直的平行四边形是菱形;
判定3:四边都相等的四边形是菱形.
菱形除了具有平行四边形的性质之外,还有“邻边相等”,但这两者其实是等价的,故若四边形ABCD 是菱形,则其4个点坐标需满足:
即根据菱形的图形性质,我们可以列出关于点坐标的 3个等式,故菱形存在性问题点坐标最多可以有3个未知量,与矩形相同.
因此就常规题型而言,菱形存在性至少有2个动点,多则有3个动点.
题型总结
(1) 2个定点+1个半动点+1个全动点; (常规)
(2) 1个定点+3个半动点. (难)
方法总结
引例1:如图,在坐标系中,A点坐标(1,1),B点坐标为(5, 4), 点C在x轴上, 点D在平面中, 求D点坐标, 使得以A、B、C、D为顶点的四边形是菱形.
思路1:先等腰,再菱形
在构成菱形的4个点中任取3个点,必构成等腰三角形,根据等腰存在性方法可先确定第3个点,
再确定第4个点.
解析:先求点 C使得△ABC是等腰三角形,再考虑点D.
(1) 当AB=AC时,
C点坐标为( ,对应D 点坐标为(
C点坐标为 ,对应D点坐标为(
(2) 当BA=BC时,
C点坐标为 (8, 0), 对应D点坐标为(4, - 3);
C点坐标为(2, 0), 对应D 点坐标为(-2, - 3).
(3) AC=BC时,
C点坐标为( , ),D点坐标为 (,s).
思路2:先平四,再菱形
设点坐标,根据平四存在性要求列出“A+C=B+D”(AC、BD为对角线),再结合一组邻边相等,得到方程组.
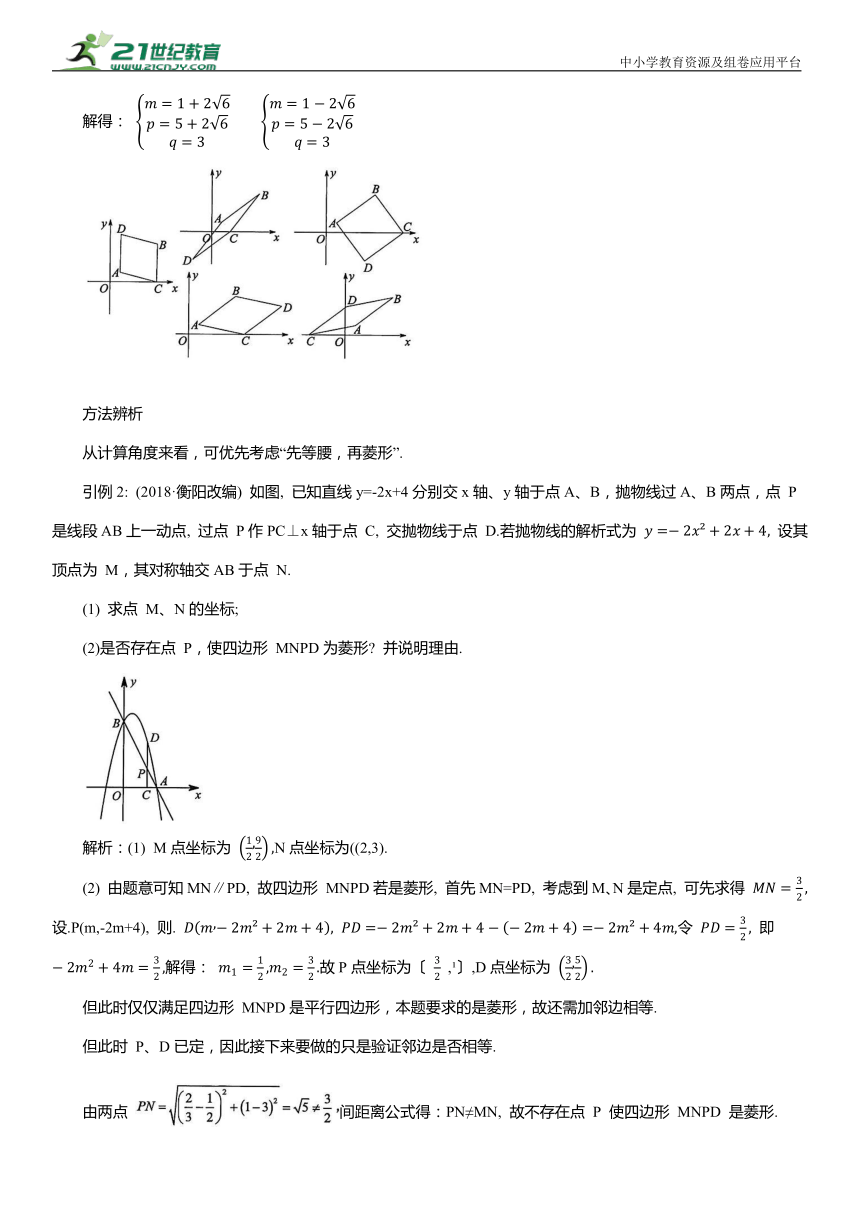
解析: 设C点坐标为(m, 0), D 点坐标为 (p, q).
(1)当AB为对角线时,由题意得:(AB和CD互相平分及AC=BC)
解得:
(2)当AC为对角线时,由题意得:(AC和BD互相平分及BA=BC)
解得: 或
(3) 当AD为对角线时,由题意得:
解得:
方法辨析
从计算角度来看,可优先考虑“先等腰,再菱形”.
引例2: (2018·衡阳改编) 如图, 已知直线y=-2x+4分别交x轴、y轴于点A、B,抛物线过A、B两点,点 P是线段AB上一动点, 过点 P作PC⊥x轴于点 C, 交抛物线于点 D.若抛物线的解析式为 设其顶点为 M,其对称轴交AB于点 N.
(1) 求点 M、N的坐标;
(2)是否存在点 P,使四边形 MNPD为菱形 并说明理由.
解析:(1) M点坐标为 N点坐标为((2,3).
(2) 由题意可知MN∥PD, 故四边形 MNPD若是菱形, 首先MN=PD, 考虑到M、N是定点, 可先求得 设.P(m,-2m+4), 则. 令 即 解得: 故P点坐标为〔 , 〕,D点坐标为
但此时仅仅满足四边形 MNPD是平行四边形,本题要求的是菱形,故还需加邻边相等.
但此时 P、D已定,因此接下来要做的只是验证邻边是否相等.
由两点间距离公式得:PN≠MN, 故不存在点 P 使四边形 MNPD 是菱形.
思考:为什么本题结论是不存在
表面上看是不满足邻边相等,究其原因,是因为M、N 是定点,P、D虽为动点但仅仅是半动点,且P、D横坐标相同,故本题只需一个字母便可表示出4个点的坐标,对于菱形四个点满足:
若只有1个未知数或2个未知数,便出现方程个数>未知量个数的情况,就有可能会无解.
方程个数<未知数个量,可能无法确定有限组解;
方程个数>未知数个量,可能会无解.
特殊图形的存在性,其动点是在线上还是在平面上,是有1个动点还是有2个动点,都是由其图形本身决定,矩形和菱形相比起平行四边形,均多一个等式,故对动点位置的要求可以有 3 个半动点或者 1 个全动点+1个半动点,若减少未知量的个数,反而可能会产生无解的情况.
真 题 演 练
综合与探究
如图,抛物线 与x轴交于A、B两点,与y轴交于C点, OA=2, OC=6, 连接AC和BC.
(1) 求抛物线的解析式;
(2)若点 M是y轴上的动点,在坐标平面内是否存在点 N,使以点A、C、M、N为顶点的四边形是菱形 若存在,请直接写出点N的坐标; 若不存在,请说明理由.
2. 如图,在平面直角坐标系中,Rt△ABC的边BC在x轴上, ∠ABC=90°, 以A 为顶点的抛物线 经过点C(3,0),交y轴于点E(0,3),动点 P在对称轴上.
(1) 求抛物线解析式;
(2) 若点 M是平面内的任意一点,在x轴上方是否存在点P,使得以点 P、M、E、C为顶点的四边形是菱形,若存在,请直接写出符合条件的 M点坐标; 若不存在,说明理由.
3. 综合与探究
如图1所示, 直线y=x+c与x轴交于点A (-4, 0), 与y轴交于点 C,抛物线 经过点A、C.
(1) 求抛物线的解析式
(2) 如图2所示,M是线段OA 的上一个动点,过点M垂直于 x 轴的直线与直线 AC 和抛物线分别交于点 P、N. 若点 P恰好是线段MN的中点,点 F是直线AC上一个动点,在坐标平面内是否存在点 D,使以点 D、F、P、M为顶点的四边形是菱形 若存在,请直接写出点D的坐标; 若不存在,请说明理由.
4. 如图,抛物线 与x轴相交于A、B两点,与y轴相交于点 C,已知抛物线的对称轴所在的直线是 点B的坐标为(4, 0).
(1) 求抛物线解析式;
(2) 若M为x轴上一动点,在抛物线上是否存在点 N,使得点 B、C、M、N构成的四边形是菱形,若存在,求出点N坐标,若不存在,请说明理由.
第5节 菱形存在性问题
1.解析: (1) 抛物线:
(2)先考虑 M点位置,即由A、C、M三点构成的三角形是等腰三角形:
①当CA=CM时, 即
M点坐标为
对应N点坐标为
②当AC=AM时, 即. M点坐标为(0, 6), 对应N点坐标为 (2, 0).
③当MA=MC时,勾股定理可求得M点坐标为 应N点坐标为
综上,N点坐标为((-2,-2 )、(-2,2 )、(2, 0)、
2.解析: (1) 抛物线:
(2)先考虑P点位置,由P、E、C三点构成的三角形是等腰三角形.
①当EC=EP时,
由 得 又点P在对称轴x=1上,勾股定理解得P点坐标为 (舍),根据点的平移推得M点坐标为(4, ).
②当CE=CP时,
即 勾股定理解得 P 点坐标为(1, )、 (舍),
根据点的平移推得M点坐标为
③当PE=PC时,
设P点坐标为(1, m),
解得: m=1, 故 P 点坐标为(1, 1),
对应的点M坐标为 (2, 2).
综上所述,M点坐标为((4, )、(-2,3+ )、(2, 2).
3.解析:(1) 抛物线解析式:
(2) 设M点坐标为(m, 0)(-4则N点坐标为 P点坐标为(m, m+4),
若P是MN中点,则
解得: (舍), 故P(-1, 3)、M(-1, 0).考虑到F点在直线AC上,故可先确定F点位置,再求得D点坐标, 当PM=PF时,
PF=3,可得 对应
当MP=MF时,
MP=MF, 可得F (-4,0), 对应D点坐标为D (-4,3).
当FP=FM时,
FP=FM, F点在 PM垂直平分线上, 可得 对应D 点坐标为
综 上 所 述 , D 点 坐 标 有
4.解析: (1) 抛物线:
(2) 本题是“两定两动”,但两个动点一个在x轴上,一个在抛物线上,均为半动点,故只需两个字母即可表示,未知量个数少于方程个数,结果可能会无解.
设 M 点坐标为(m, 0), N 点坐标为 又B(4, 0)、C(0, 2).
当 CB为对角线时,取对角线互相平分及MB=MC,可得:
方程组无解,故这种情况不存在;
当CM为对角线时,取对角线互相平分及BC=BM,可得:
方程组依然无解; 这种情况也不存在;
当 CN为对角线时,取对角线互相平分及CB=CM,可得:
方程组还是无解.
综上,不存在这样的M、N.
前言:与矩形相似,菱形存在性问题也可从两个角度来考虑,即从等腰到菱形或从平四到菱形,具体方法选择还需具体问题具体分析.
中小学教育资源及组卷应用平台
知 识 导 航
问题探究
先从菱形的判定着手考虑:
判定1:有一组邻边相等的平行四边形菱形;
判定2:对角线互相垂直的平行四边形是菱形;
判定3:四边都相等的四边形是菱形.
菱形除了具有平行四边形的性质之外,还有“邻边相等”,但这两者其实是等价的,故若四边形ABCD 是菱形,则其4个点坐标需满足:
即根据菱形的图形性质,我们可以列出关于点坐标的 3个等式,故菱形存在性问题点坐标最多可以有3个未知量,与矩形相同.
因此就常规题型而言,菱形存在性至少有2个动点,多则有3个动点.
题型总结
(1) 2个定点+1个半动点+1个全动点; (常规)
(2) 1个定点+3个半动点. (难)
方法总结
引例1:如图,在坐标系中,A点坐标(1,1),B点坐标为(5, 4), 点C在x轴上, 点D在平面中, 求D点坐标, 使得以A、B、C、D为顶点的四边形是菱形.
思路1:先等腰,再菱形
在构成菱形的4个点中任取3个点,必构成等腰三角形,根据等腰存在性方法可先确定第3个点,
再确定第4个点.
解析:先求点 C使得△ABC是等腰三角形,再考虑点D.
(1) 当AB=AC时,
C点坐标为( ,对应D 点坐标为(
C点坐标为 ,对应D点坐标为(
(2) 当BA=BC时,
C点坐标为 (8, 0), 对应D点坐标为(4, - 3);
C点坐标为(2, 0), 对应D 点坐标为(-2, - 3).
(3) AC=BC时,
C点坐标为( , ),D点坐标为 (,s).
思路2:先平四,再菱形
设点坐标,根据平四存在性要求列出“A+C=B+D”(AC、BD为对角线),再结合一组邻边相等,得到方程组.
解析: 设C点坐标为(m, 0), D 点坐标为 (p, q).
(1)当AB为对角线时,由题意得:(AB和CD互相平分及AC=BC)
解得:
(2)当AC为对角线时,由题意得:(AC和BD互相平分及BA=BC)
解得: 或
(3) 当AD为对角线时,由题意得:
解得:
方法辨析
从计算角度来看,可优先考虑“先等腰,再菱形”.
引例2: (2018·衡阳改编) 如图, 已知直线y=-2x+4分别交x轴、y轴于点A、B,抛物线过A、B两点,点 P是线段AB上一动点, 过点 P作PC⊥x轴于点 C, 交抛物线于点 D.若抛物线的解析式为 设其顶点为 M,其对称轴交AB于点 N.
(1) 求点 M、N的坐标;
(2)是否存在点 P,使四边形 MNPD为菱形 并说明理由.
解析:(1) M点坐标为 N点坐标为((2,3).
(2) 由题意可知MN∥PD, 故四边形 MNPD若是菱形, 首先MN=PD, 考虑到M、N是定点, 可先求得 设.P(m,-2m+4), 则. 令 即 解得: 故P点坐标为〔 , 〕,D点坐标为
但此时仅仅满足四边形 MNPD是平行四边形,本题要求的是菱形,故还需加邻边相等.
但此时 P、D已定,因此接下来要做的只是验证邻边是否相等.
由两点间距离公式得:PN≠MN, 故不存在点 P 使四边形 MNPD 是菱形.
思考:为什么本题结论是不存在
表面上看是不满足邻边相等,究其原因,是因为M、N 是定点,P、D虽为动点但仅仅是半动点,且P、D横坐标相同,故本题只需一个字母便可表示出4个点的坐标,对于菱形四个点满足:
若只有1个未知数或2个未知数,便出现方程个数>未知量个数的情况,就有可能会无解.
方程个数<未知数个量,可能无法确定有限组解;
方程个数>未知数个量,可能会无解.
特殊图形的存在性,其动点是在线上还是在平面上,是有1个动点还是有2个动点,都是由其图形本身决定,矩形和菱形相比起平行四边形,均多一个等式,故对动点位置的要求可以有 3 个半动点或者 1 个全动点+1个半动点,若减少未知量的个数,反而可能会产生无解的情况.
真 题 演 练
综合与探究
如图,抛物线 与x轴交于A、B两点,与y轴交于C点, OA=2, OC=6, 连接AC和BC.
(1) 求抛物线的解析式;
(2)若点 M是y轴上的动点,在坐标平面内是否存在点 N,使以点A、C、M、N为顶点的四边形是菱形 若存在,请直接写出点N的坐标; 若不存在,请说明理由.
2. 如图,在平面直角坐标系中,Rt△ABC的边BC在x轴上, ∠ABC=90°, 以A 为顶点的抛物线 经过点C(3,0),交y轴于点E(0,3),动点 P在对称轴上.
(1) 求抛物线解析式;
(2) 若点 M是平面内的任意一点,在x轴上方是否存在点P,使得以点 P、M、E、C为顶点的四边形是菱形,若存在,请直接写出符合条件的 M点坐标; 若不存在,说明理由.
3. 综合与探究
如图1所示, 直线y=x+c与x轴交于点A (-4, 0), 与y轴交于点 C,抛物线 经过点A、C.
(1) 求抛物线的解析式
(2) 如图2所示,M是线段OA 的上一个动点,过点M垂直于 x 轴的直线与直线 AC 和抛物线分别交于点 P、N. 若点 P恰好是线段MN的中点,点 F是直线AC上一个动点,在坐标平面内是否存在点 D,使以点 D、F、P、M为顶点的四边形是菱形 若存在,请直接写出点D的坐标; 若不存在,请说明理由.
4. 如图,抛物线 与x轴相交于A、B两点,与y轴相交于点 C,已知抛物线的对称轴所在的直线是 点B的坐标为(4, 0).
(1) 求抛物线解析式;
(2) 若M为x轴上一动点,在抛物线上是否存在点 N,使得点 B、C、M、N构成的四边形是菱形,若存在,求出点N坐标,若不存在,请说明理由.
第5节 菱形存在性问题
1.解析: (1) 抛物线:
(2)先考虑 M点位置,即由A、C、M三点构成的三角形是等腰三角形:
①当CA=CM时, 即
M点坐标为
对应N点坐标为
②当AC=AM时, 即. M点坐标为(0, 6), 对应N点坐标为 (2, 0).
③当MA=MC时,勾股定理可求得M点坐标为 应N点坐标为
综上,N点坐标为((-2,-2 )、(-2,2 )、(2, 0)、
2.解析: (1) 抛物线:
(2)先考虑P点位置,由P、E、C三点构成的三角形是等腰三角形.
①当EC=EP时,
由 得 又点P在对称轴x=1上,勾股定理解得P点坐标为 (舍),根据点的平移推得M点坐标为(4, ).
②当CE=CP时,
即 勾股定理解得 P 点坐标为(1, )、 (舍),
根据点的平移推得M点坐标为
③当PE=PC时,
设P点坐标为(1, m),
解得: m=1, 故 P 点坐标为(1, 1),
对应的点M坐标为 (2, 2).
综上所述,M点坐标为((4, )、(-2,3+ )、(2, 2).
3.解析:(1) 抛物线解析式:
(2) 设M点坐标为(m, 0)(-4
若P是MN中点,则
解得: (舍), 故P(-1, 3)、M(-1, 0).考虑到F点在直线AC上,故可先确定F点位置,再求得D点坐标, 当PM=PF时,
PF=3,可得 对应
当MP=MF时,
MP=MF, 可得F (-4,0), 对应D点坐标为D (-4,3).
当FP=FM时,
FP=FM, F点在 PM垂直平分线上, 可得 对应D 点坐标为
综 上 所 述 , D 点 坐 标 有
4.解析: (1) 抛物线:
(2) 本题是“两定两动”,但两个动点一个在x轴上,一个在抛物线上,均为半动点,故只需两个字母即可表示,未知量个数少于方程个数,结果可能会无解.
设 M 点坐标为(m, 0), N 点坐标为 又B(4, 0)、C(0, 2).
当 CB为对角线时,取对角线互相平分及MB=MC,可得:
方程组无解,故这种情况不存在;
当CM为对角线时,取对角线互相平分及BC=BM,可得:
方程组依然无解; 这种情况也不存在;
当 CN为对角线时,取对角线互相平分及CB=CM,可得:
方程组还是无解.
综上,不存在这样的M、N.
同课章节目录
