2025年中考数学压轴题二轮专题复习讲练 第5章 特殊图形存在性问题第4节 矩形存在性问题(含解析)
文档属性
| 名称 | 2025年中考数学压轴题二轮专题复习讲练 第5章 特殊图形存在性问题第4节 矩形存在性问题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 211.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览


文档简介
第4节 矩形存在性问题
前言:在平行四边形的基础上,可继续探究矩形及菱形的存在性问题,分析不同图形之间的联系与区别,可找到正确解题之道.
中小学教育资源及组卷应用平台
知 识 导 航
问题探究
先从矩形的判定着手考虑:
判定1:有一个角是直角的平行四边形;
判定2:对角线相等的平行四边形;
判定3:有三个角为直角的四边形.
矩形除了具有平行四边形的性质之外,还有“对角线相等”,因此相比起平行四边形,坐标系中的矩形ABCD满足以下3个等式:
因此在矩形存在性问题最多可以有3个未知量,代入可以得到三元一次方程组,可解.
确定了有3个未知量,则可判断常见矩形存在性问题至少有2个动点,多则可以有3个.
题型总结
(1) 2个定点+1个半动点+1个全动点; (常规)
(2) 1个定点+3个半动点.(难)
方法总结
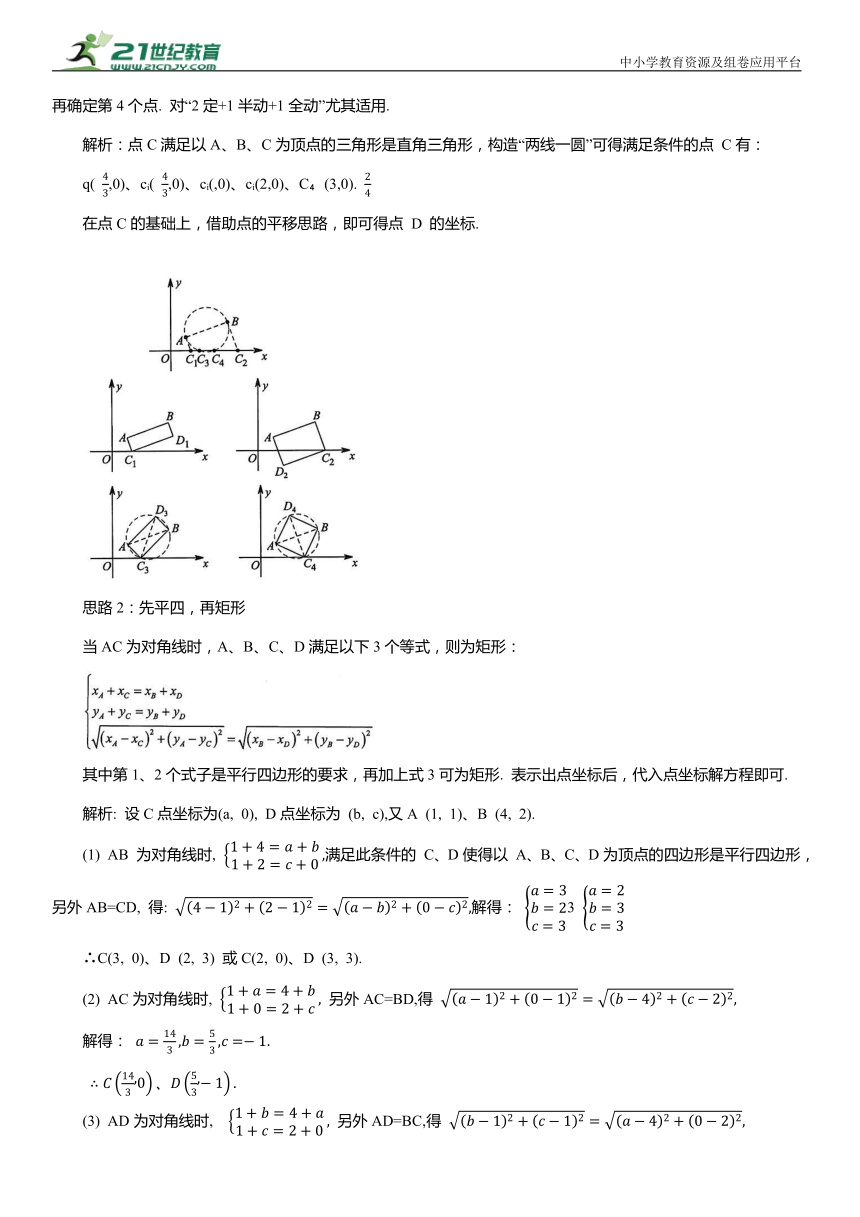
引例1: 已知A(1, 1)、B(4, 2), 点 C在x轴上, 点 D在平面中,且以A、B、C、D为顶点的四边形是矩形,求D点坐标.
思路1:先直角,再矩形
在构成矩形的4个点中任取3个点,必构成直角三角形,以此为出发点,可先确定其中3个点构造直角三角形,再确定第4个点. 对“2定+1半动+1全动”尤其适用.
解析:点C满足以A、B、C为顶点的三角形是直角三角形,构造“两线一圆”可得满足条件的点 C有:
q( ,0)、c ( ,0)、c (,0)、c (2,0)、C (3,0).
在点C的基础上,借助点的平移思路,即可得点 D 的坐标.
思路2:先平四,再矩形
当AC为对角线时,A、B、C、D满足以下3个等式,则为矩形:
其中第1、2个式子是平行四边形的要求,再加上式3可为矩形. 表示出点坐标后,代入点坐标解方程即可.
解析: 设C点坐标为(a, 0), D点坐标为 (b, c),又A (1, 1)、B (4, 2).
(1) AB 为对角线时, 满足此条件的 C、D使得以 A、B、C、D为顶点的四边形是平行四边形,另外AB=CD, 得: 解得: 3
∴C(3, 0)、D (2, 3) 或C(2, 0)、D (3, 3).
(2) AC为对角线时, 另外AC=BD,得
解得:
(3) AD为对角线时, 另外AD=BC,得
解得:
综上, 点D坐标为(2,3)或(3,3)或 或( ,1).
方法辨析
从计算角度来看,可优先考虑“先直角,再矩形”.
引例2:(2018·辽阳改编) 如图, 直线y=x-3与坐标轴交于 A、B两点,抛物线 经过点 B,与直线y=x-3交于点E(8, 5), 且与x轴交于C、D两点.
(1) 求抛物线的解析式;
(2) 点P 在抛物线上,在坐标平面内是否存在点 Q,使得以点 P、Q、B、C为顶点的四边形是矩形 若存在,请直接写出点Q的坐标; 若不存在,请说明理由.
解析: (1) 抛物线:
(2) 先确定 P 点使得由 P、B、C构成的三角形为直角三角形,设P 点坐标为
①当∠PBC=90°时, 构造三垂直相似: △PEB∽△BFC,
BE=-m, BF=6-0=6, CF=3,
由相似可知: 即
解得: (舍),代入得 P 点坐标为(-4,5),根据点的平移可知对应的Q 点坐标为(2,8).
②当∠PCB=90°时, 同理可构造相似:
解得: m =-10, m =6 (舍)
代入得 P 点坐标为(-10,32),根据点的平移可知对应的Q点坐标为(-16, 29).
另外以BC为直径作圆,与抛物线并无交点,
∴不存在以 P点为直角顶点的情况.
综上所述, Q点坐标为(2, 8) 或(-16, 29).
真 题 演 练
1. 如图, 抛物线 交 x轴于点 A、B, 交y轴于点 C. 点 B 的坐标为(3, 0) 点 C的坐标为(0,3),点C与点 D关于抛物线的对称轴对称.
(1) 求抛物线的解析式;
(2) 若点 P 为抛物线对称轴上一点, 连接BD, 以PD, PB为边作平行四边形 PDNB,是否存在这样的点 P,使得平行四边形 PDNB 是矩形 若存在,请求出 tan∠BDN的值; 若不存在,请说明理由.
2. 如图, 抛物线 与x轴交于点A (-1, 0), 点 B (-3, 0), 且OB=OC.
(1) 求抛物线的解析式;
(2) 抛物线上两点 M, N, 点M的横坐标为m, 点N 的横坐标为 m+4. 点D 是抛物线上 M、N之间的动点,过点D作y轴的平行线交 MN于点E.
①求 DE的最大值;
②点D关于点E的对称点为F,当m为何值时,四边形 MDNF为矩形.
3. 如图:在平面直角坐标系中,直线 与x轴交于A,经过点A的抛物线 的对称轴是
(1) 求抛物线的解析式;
(2) 平移直线 l 经过原点 O, 得到直线 m, 点P 是直线 m上任意一点, PB⊥x轴于点B, PC⊥y轴于点 C, 若点 E 在线段 OB 上, 点F 在线段 OC 的延长线上, 连接PE, PF, 且PF=3PE. 求证: PE⊥PF;
(3)若(2)中的点P坐标为(6, 2), 点E是x轴上的点,点 F是 y轴上的点,当 PE⊥PF时,抛物线上是否存在点 Q,使四边形 PEQF 是矩形 如果存在,请求出点Q的坐标,如果不存在,请说明理由.
第4节 矩形存在性问题
1.解析: (1) 抛物线:
(2) 已知点 P在对称轴直线x=1上,可求得P 点坐标使得∠P=90°. 如图,记对称轴与x轴交点为E点, 过点D作DF垂直对称轴于 F点.
当P点满足 时, 即可得: △PFD∽△BEP.
设PE=a, PF=b, 则 解得: 或
当P点坐标为(-1, 2) 时,
当P点坐标为(-1, 1) 时, tan∠BDN=tan∠PBD=1.
2.解析: (1) 抛物线:
(2)①由题意可知:
由题意得:
直线MN:
整理得:
设 D 点 坐 标为 则 E 点 坐 标为
故当d=m+2时, DE取到最大值为4.
②若四边形 MDNF 是矩形,根据对角线互相平分,则E 点必为 MN 中点,故E 点横坐标为 m+2,则D 点横坐标也为m+2, 且由①可知, 此时DE=4,
又矩形对角线相等,因此只要满足MN=8,则有矩形 MDNF.
解得:
∴当m为 或 时, 四边形 MDNF 是矩形.
补充:考虑到第①问中已经得到了 DE=4,故本题优先考虑利用对角线相等求解,事实上,构造三垂直使△MDN是直角三角形,也可以解决问题.
构造△MED∽△DFN,
即
同样可解得:
3.解析:(1)由题意得: A(4,0), 根据对称轴可知: a=1,将(4, 0) 代入解析式得: c=-4,
∴抛物线:
(2) 易证△PCF∽△PBE, 可得; PE⊥PF.
(3) P 点为定点(6, 2), E是x轴上动点, F是y轴上动点,Q是抛物线上动点,且四边形为 PEQF,确定了点的顺序,无需分类讨论.
法1: 设.E(a, 0)、F(0, b)、 又A(6,
2),由矩形可列方程组:
解得: 或
∴Q 点坐标为(2, - 6)、(-2, 6).
这种做法思路并不麻烦,难点在于解方程组,将式 1、式2代入式 3 中,两边平方之后移项构造平方差,可简便得解.
法2: 有问题(2)作铺垫, 当PE⊥PF时, 始终有△PCF∽△PBE, 且相似比为3: 1,
①当E点在B点左侧时,F点在 C点上方,
不妨设BE=m, 则CF=3m,
根据点的平移可得:Q点坐标为(-m,3m),
代入抛物线解析式: 解得:
(舍). 此时Q点坐标为(2, - 6);
②当E点在 B 点右侧时,F点在 C点下方,
同理可得m的值为-2, 对应Q点坐标为(-2, 6).
综上所述, Q点坐标为 (2, - 6)、(-2, 6).
前言:在平行四边形的基础上,可继续探究矩形及菱形的存在性问题,分析不同图形之间的联系与区别,可找到正确解题之道.
中小学教育资源及组卷应用平台
知 识 导 航
问题探究
先从矩形的判定着手考虑:
判定1:有一个角是直角的平行四边形;
判定2:对角线相等的平行四边形;
判定3:有三个角为直角的四边形.
矩形除了具有平行四边形的性质之外,还有“对角线相等”,因此相比起平行四边形,坐标系中的矩形ABCD满足以下3个等式:
因此在矩形存在性问题最多可以有3个未知量,代入可以得到三元一次方程组,可解.
确定了有3个未知量,则可判断常见矩形存在性问题至少有2个动点,多则可以有3个.
题型总结
(1) 2个定点+1个半动点+1个全动点; (常规)
(2) 1个定点+3个半动点.(难)
方法总结
引例1: 已知A(1, 1)、B(4, 2), 点 C在x轴上, 点 D在平面中,且以A、B、C、D为顶点的四边形是矩形,求D点坐标.
思路1:先直角,再矩形
在构成矩形的4个点中任取3个点,必构成直角三角形,以此为出发点,可先确定其中3个点构造直角三角形,再确定第4个点. 对“2定+1半动+1全动”尤其适用.
解析:点C满足以A、B、C为顶点的三角形是直角三角形,构造“两线一圆”可得满足条件的点 C有:
q( ,0)、c ( ,0)、c (,0)、c (2,0)、C (3,0).
在点C的基础上,借助点的平移思路,即可得点 D 的坐标.
思路2:先平四,再矩形
当AC为对角线时,A、B、C、D满足以下3个等式,则为矩形:
其中第1、2个式子是平行四边形的要求,再加上式3可为矩形. 表示出点坐标后,代入点坐标解方程即可.
解析: 设C点坐标为(a, 0), D点坐标为 (b, c),又A (1, 1)、B (4, 2).
(1) AB 为对角线时, 满足此条件的 C、D使得以 A、B、C、D为顶点的四边形是平行四边形,另外AB=CD, 得: 解得: 3
∴C(3, 0)、D (2, 3) 或C(2, 0)、D (3, 3).
(2) AC为对角线时, 另外AC=BD,得
解得:
(3) AD为对角线时, 另外AD=BC,得
解得:
综上, 点D坐标为(2,3)或(3,3)或 或( ,1).
方法辨析
从计算角度来看,可优先考虑“先直角,再矩形”.
引例2:(2018·辽阳改编) 如图, 直线y=x-3与坐标轴交于 A、B两点,抛物线 经过点 B,与直线y=x-3交于点E(8, 5), 且与x轴交于C、D两点.
(1) 求抛物线的解析式;
(2) 点P 在抛物线上,在坐标平面内是否存在点 Q,使得以点 P、Q、B、C为顶点的四边形是矩形 若存在,请直接写出点Q的坐标; 若不存在,请说明理由.
解析: (1) 抛物线:
(2) 先确定 P 点使得由 P、B、C构成的三角形为直角三角形,设P 点坐标为
①当∠PBC=90°时, 构造三垂直相似: △PEB∽△BFC,
BE=-m, BF=6-0=6, CF=3,
由相似可知: 即
解得: (舍),代入得 P 点坐标为(-4,5),根据点的平移可知对应的Q 点坐标为(2,8).
②当∠PCB=90°时, 同理可构造相似:
解得: m =-10, m =6 (舍)
代入得 P 点坐标为(-10,32),根据点的平移可知对应的Q点坐标为(-16, 29).
另外以BC为直径作圆,与抛物线并无交点,
∴不存在以 P点为直角顶点的情况.
综上所述, Q点坐标为(2, 8) 或(-16, 29).
真 题 演 练
1. 如图, 抛物线 交 x轴于点 A、B, 交y轴于点 C. 点 B 的坐标为(3, 0) 点 C的坐标为(0,3),点C与点 D关于抛物线的对称轴对称.
(1) 求抛物线的解析式;
(2) 若点 P 为抛物线对称轴上一点, 连接BD, 以PD, PB为边作平行四边形 PDNB,是否存在这样的点 P,使得平行四边形 PDNB 是矩形 若存在,请求出 tan∠BDN的值; 若不存在,请说明理由.
2. 如图, 抛物线 与x轴交于点A (-1, 0), 点 B (-3, 0), 且OB=OC.
(1) 求抛物线的解析式;
(2) 抛物线上两点 M, N, 点M的横坐标为m, 点N 的横坐标为 m+4. 点D 是抛物线上 M、N之间的动点,过点D作y轴的平行线交 MN于点E.
①求 DE的最大值;
②点D关于点E的对称点为F,当m为何值时,四边形 MDNF为矩形.
3. 如图:在平面直角坐标系中,直线 与x轴交于A,经过点A的抛物线 的对称轴是
(1) 求抛物线的解析式;
(2) 平移直线 l 经过原点 O, 得到直线 m, 点P 是直线 m上任意一点, PB⊥x轴于点B, PC⊥y轴于点 C, 若点 E 在线段 OB 上, 点F 在线段 OC 的延长线上, 连接PE, PF, 且PF=3PE. 求证: PE⊥PF;
(3)若(2)中的点P坐标为(6, 2), 点E是x轴上的点,点 F是 y轴上的点,当 PE⊥PF时,抛物线上是否存在点 Q,使四边形 PEQF 是矩形 如果存在,请求出点Q的坐标,如果不存在,请说明理由.
第4节 矩形存在性问题
1.解析: (1) 抛物线:
(2) 已知点 P在对称轴直线x=1上,可求得P 点坐标使得∠P=90°. 如图,记对称轴与x轴交点为E点, 过点D作DF垂直对称轴于 F点.
当P点满足 时, 即可得: △PFD∽△BEP.
设PE=a, PF=b, 则 解得: 或
当P点坐标为(-1, 2) 时,
当P点坐标为(-1, 1) 时, tan∠BDN=tan∠PBD=1.
2.解析: (1) 抛物线:
(2)①由题意可知:
由题意得:
直线MN:
整理得:
设 D 点 坐 标为 则 E 点 坐 标为
故当d=m+2时, DE取到最大值为4.
②若四边形 MDNF 是矩形,根据对角线互相平分,则E 点必为 MN 中点,故E 点横坐标为 m+2,则D 点横坐标也为m+2, 且由①可知, 此时DE=4,
又矩形对角线相等,因此只要满足MN=8,则有矩形 MDNF.
解得:
∴当m为 或 时, 四边形 MDNF 是矩形.
补充:考虑到第①问中已经得到了 DE=4,故本题优先考虑利用对角线相等求解,事实上,构造三垂直使△MDN是直角三角形,也可以解决问题.
构造△MED∽△DFN,
即
同样可解得:
3.解析:(1)由题意得: A(4,0), 根据对称轴可知: a=1,将(4, 0) 代入解析式得: c=-4,
∴抛物线:
(2) 易证△PCF∽△PBE, 可得; PE⊥PF.
(3) P 点为定点(6, 2), E是x轴上动点, F是y轴上动点,Q是抛物线上动点,且四边形为 PEQF,确定了点的顺序,无需分类讨论.
法1: 设.E(a, 0)、F(0, b)、 又A(6,
2),由矩形可列方程组:
解得: 或
∴Q 点坐标为(2, - 6)、(-2, 6).
这种做法思路并不麻烦,难点在于解方程组,将式 1、式2代入式 3 中,两边平方之后移项构造平方差,可简便得解.
法2: 有问题(2)作铺垫, 当PE⊥PF时, 始终有△PCF∽△PBE, 且相似比为3: 1,
①当E点在B点左侧时,F点在 C点上方,
不妨设BE=m, 则CF=3m,
根据点的平移可得:Q点坐标为(-m,3m),
代入抛物线解析式: 解得:
(舍). 此时Q点坐标为(2, - 6);
②当E点在 B 点右侧时,F点在 C点下方,
同理可得m的值为-2, 对应Q点坐标为(-2, 6).
综上所述, Q点坐标为 (2, - 6)、(-2, 6).
同课章节目录
