2025年中考数学压轴题二轮专题复习讲练第6章 坐标系中的角 第1节 坐标系中的特殊角(含解析)
文档属性
| 名称 | 2025年中考数学压轴题二轮专题复习讲练第6章 坐标系中的角 第1节 坐标系中的特殊角(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 424.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 00:00:00 | ||
图片预览



文档简介
第6章 坐标系中的角
第1节 坐标系中的特殊角
前言:坐标系中关于角的探究形式多样,从最基础的角的认识开始,本节讨论关于特殊角的相关内容,从特殊到一般,发现总结关于角处理的常规方法.
知识导航
什么是特殊角
说到特殊角我们很快就能想到比如30°、45°、60°、90°等,事实上,之所以以上角能称为特殊角,关键在于这些角的三角函数值特殊,比如同为整十,为什么我们会将 60°称为特殊角,而50°便不是,原因很简单, 而我们并不知道50°的三角函数值.
因此角度特殊不在于这个角是多少度,而在于其三角函数值是否有特殊值,所以除了常见的 30°、45°、60°,我们可以扩充一下特殊角的范围.
(1) 一组特殊角α与β
引例1:如图所示的网格是正方形网格,则∠PAB+∠PBA= °. (点A、B、P是网格线交点).
解析: 如图, ∠PAB+∠PBA=∠BPQ=45°
(2) 2α与2β的三角函数值
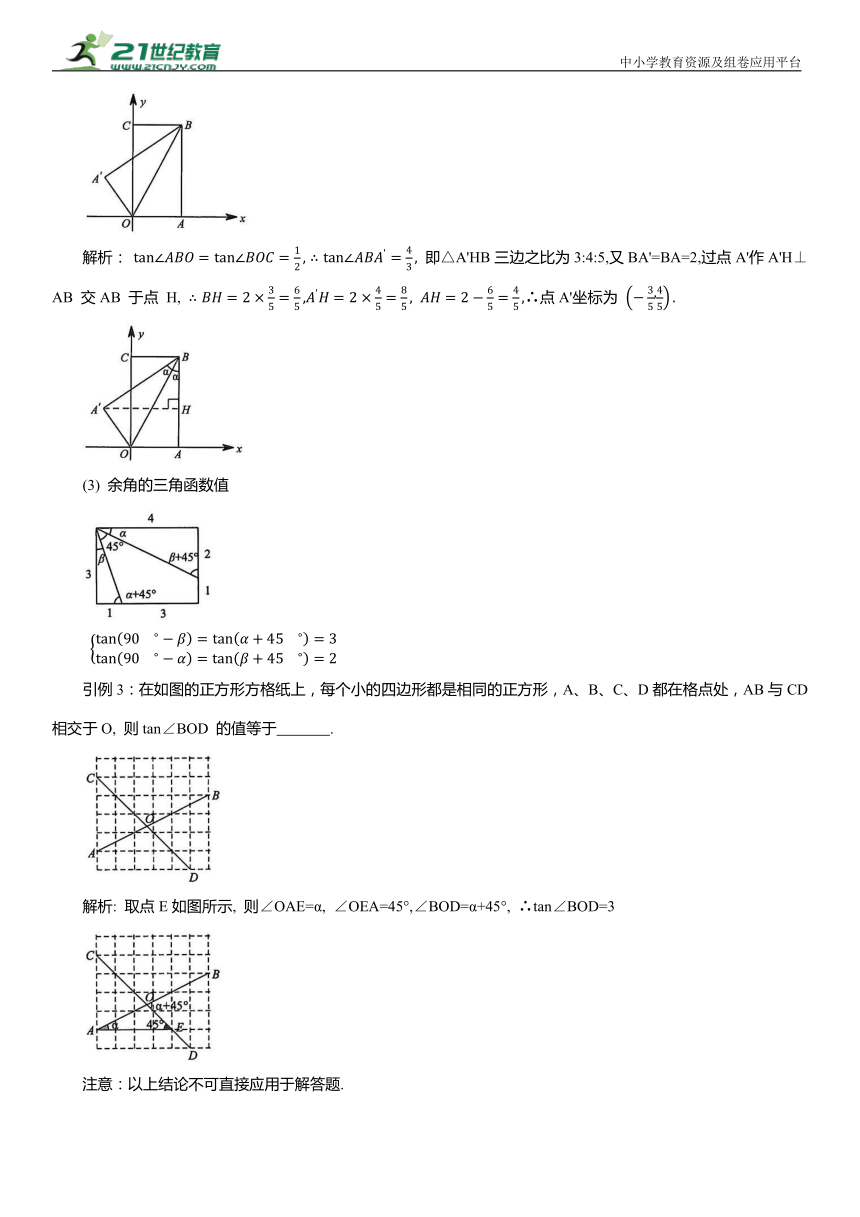
引例2 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片 OABC 沿 OB 折叠, 使点 A 落在点A'的位置, 若 则点A'的坐标为 .
解析: 即△A'HB三边之比为3:4:5,又BA'=BA=2,过点A'作A'H⊥AB 交AB 于点 H, ∴点A'坐标为
中小学教育资源及组卷应用平台
(3) 余角的三角函数值
引例3:在如图的正方形方格纸上,每个小的四边形都是相同的正方形,A、B、C、D都在格点处,AB与CD相交于O, 则tan∠BOD 的值等于 .
解析: 取点E如图所示, 则∠OAE=α, ∠OEA=45°,∠BOD=α+45°, ∴tan∠BOD=3
注意:以上结论不可直接应用于解答题.
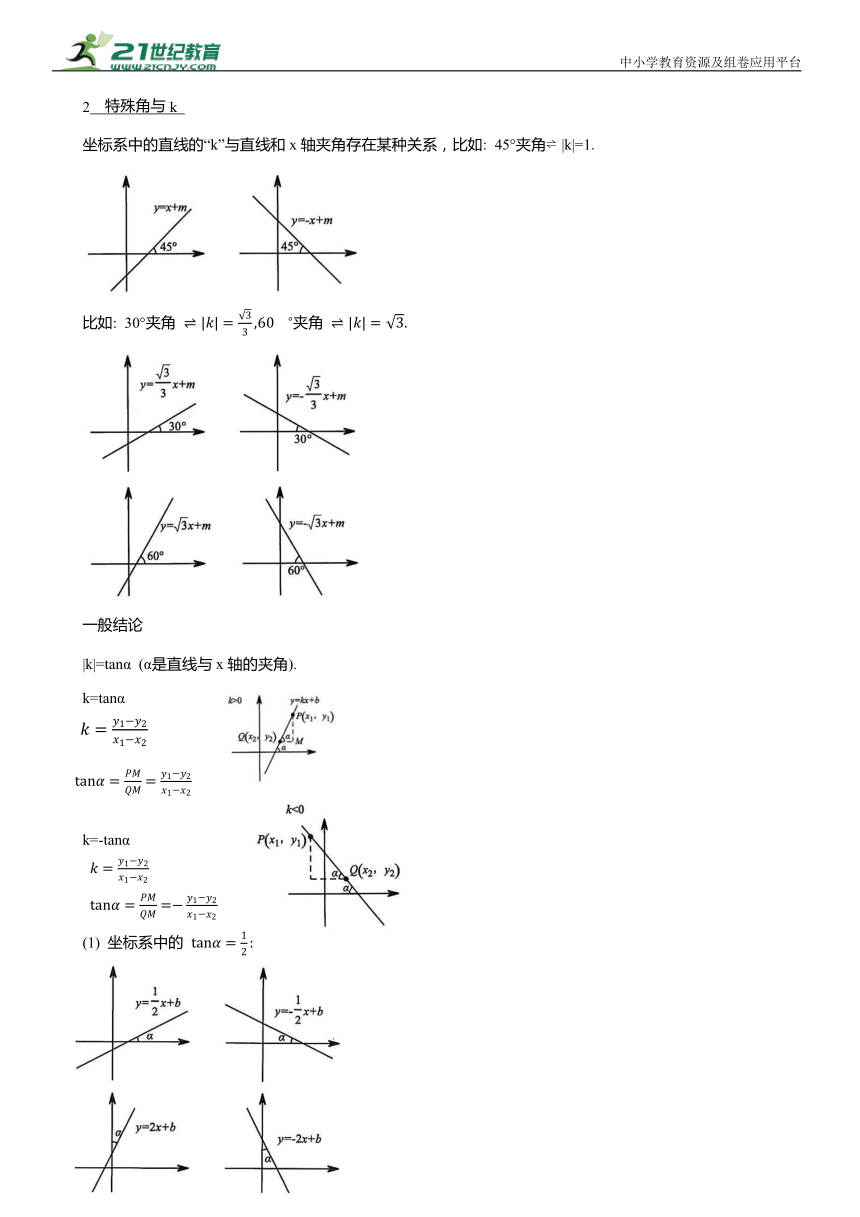
2 特殊角与k
坐标系中的直线的“k”与直线和x轴夹角存在某种关系,比如: 45°夹角 |k|=1.
比如: 30°夹角 夹角
一般结论
|k|=tanα (α是直线与x轴的夹角).
k=tanα
k=-tanα
(1) 坐标系中的
(2) 坐标系中的
引例4:如图,在平面直角坐标系中,一次函数y=2x-1的图像分别交x、y轴于点A、B, 将直线AB绕点 B 顺时针旋转 45°,交x轴于点 C,则直线 BC的函数表达式是 .
解析:根据解析式可知
∵OB=1, ∴OC=3, ∴直线BC解析式为
特殊角的构造
在坐标系中构造定角,从其三角函数值着手:
思路1:构造三垂直相似(或全等);
思路2:通过三角函数值化“角度条件”为“直线k”.
引例5:如图,在平面直线坐标系中,直线AB 解析式为 点M(2, 1) 是直线AB上一点, 将直线AB绕点M顺时针旋转45°得到直线 CD,则 CD解析式是 .
思路1:构造三垂直全等(或相似)
过点O作OP⊥AB交 CD于 P 点, 分别过 M、P向x轴作垂线, 垂足为E、F点.
可得: △OEM≌△PFO,
∴PF=OE=2, OF=ME=1, 故P 点坐标为(-1, 2),
结合P、M坐标可解直线 CD解析式:
思路2:利用特殊角的三角函数值.
过M点作MN∥x轴,
则
直线CD的增减性为y随着x的增大而减小,故 ∴CD解析式: 化简得:
45°角的构造
引例6: 如图, 抛物线 过点A (3, 2), 且与直线 交于B、C两点, 点B的坐标为(4, m).
(1) 求抛物线的解析式;
(2) 设点 M为抛物线的顶点,在y轴上是否存在点 Q,使∠AQM=45° 若存在,求点Q的坐标; 若不存在,请说明理由.
解析: (1) 抛物线:
(2) 思路1: 构造三垂直.
如图, AN⊥AQ交直线QM于N点,△ANQ 即为等腰直角三角形,设Q点坐标为(0, m), 又M点坐标为(1, 4),
可得直线QM解析式为: y=(4-m)x+m,
如上右图构造三垂直全等: △QEA≌△AFN,可得: AF=QE=3, NF=AE=2-m,
∴N点坐标为(m+1,5),
将点N代入直线QM解析式: (4-m)(m+1)+m=5,
解得:
∴Q点坐标为( 或((0,2- ).
思路2:圆周角定理
已知点A (3, 2), 可得M点坐标为(1, 4),
过点A作AP 垂直对称轴交对称轴于 P 点,
则△APM是等腰直角三角形, 其中∠APM=90°.
构造∠AQM=45°, 即
如下图,以点 P 为圆心,PA 为半径作圆,与y 轴交点即为所求Q点.
考虑半径 PA=2, 则 PQ=2, 又点 P 在对称轴x=1 上, 点 Q在y轴上,不难求得Q点坐标为(0,2+ )或(0,2- ).
思路概括
关于45°角的构造,常见思路有:
(1) 构造等腰直角三角形,通过三垂直全等计算;
(2) 构造辅助圆,由90°圆心角可得45°圆周角.
真 题 演 练
1. 如图,在平面直角坐标系xOy中,直线y=-x+m分别交x轴、y轴于 A、B 两点, 已知点 C (2,0), 点 P 为线段 OB的中点, 连接 PA、PC, 若∠CPA=∠ABO, 则 m 的值是
2. 如图, 在矩形ABCD中, BC=8, CD=6,将△ABE沿BE 折叠, 使点A 恰好落在对角线 BD 上F处,则DE的长是( )
A. 3 B. C.5
3. 在正方形 ABCD 中, 边长为 6, BE=2AE, 连接 DE, 在AD、BC上分别存在点 G、F, 连接GF交 DE于H点, 且∠GHD=45°, 求线段 FG= .
4. 如图, 直线y=x-3与坐标轴交于A、B两点,抛物线 经过点 B, 与直线y=x-3交于点E (8, 5), 且与x轴交于C, D两点.
(1) 求抛物线的解析式;
(2)抛物线上有一点 M, 当∠MBE=75°时, 求点 M横坐标.
5. 如图, 在平面直角坐标系中, Rt△ABC的斜边AB在x轴上, 点 C在y轴上, ∠ACB=90°, OA、OB 的长分别是一元二次方程 的两个根(OA(1) 求点 C的坐标;
(2)连接AD,当AD平分∠CAB时,求直线AD的解析式.
6. 如图, 抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点 C,直线l与抛物线交于A、D两点,与y轴交于点E,点D 的坐标为(4, - 3).
(1) 请直接写出A、B两点的坐标及直线l的函数表达式;
(2) 若点Q是y轴上的点, 且∠ADQ=45°, 求点 Q 的坐标.
7. 如图, 抛物线 经过点A(-1, 0)、B(4, 0), 交y轴于点 C.
(1) 求抛物线的解析式;
(2) 将直线BC绕点 B顺时针旋转45°,与抛物线交于另一点E, 求BE的长.
第1节 坐标系中的特殊角
1.解析:∠PAO=α,∠APC=45°,∴∠OPC=β,∴OP=6,OA=12,m=12.
2.C.
考虑 故选C.
3.解析:观察发现 且∠GHD=45°,考虑 GF可动, 平移GH, 将α、β、45°汇于直角处,可知
4.解析: (1) 抛物线:
(2)①当M点在直线BE上方时,如下左图,若∠MBE=75°,考虑到∠OBE=45°,
则∠OBM=30°, 即直线BM与x轴的夹角为60°,
又B点坐标为(0,-3),∴直线BM的解析式为:
联立方程:
解得: (舍),
∴M点的横坐标为
②当 M 点在直线 BE 下方时, 如上右图, 过点 B 作 BF∥x轴, 则∠EBF=45°, 若∠MBE=75°, 则∠MBF=30°,∴直线BM与x轴夹角为30°, 又B 点坐标为(0, - 3),
故直线BM解析式为:
联立方程:
解得: (舍), ∴M点横坐标为 综上所述,M点横坐标为 或
5.解析: (1) C段坐标为 (0, 12);
(2) 已知直线 AD 上的点 A 坐标,∴求出点 D 坐标或者求出直线的k,即可求出直线AD的解析式.
思路1: 求D点.
易证△ACD≌△AED,∴AC=AE,CD=ED,设ED=x,则CD=x,BD=20-x, 又BE=10, 可得方程:
解得: 故D点坐标为(6,
直线AD解析式为:
思路2: 求k.
易得:
(需证明)
∴直线AD解析式为:
6.解析:: (1)A(-2, 0)、B(6, 0),
直线l的解析式为
(2)当点Q在y轴正半轴上时,如下左图,过点A作AF⊥AD且AF=AD, 连接DF, 与y轴交点即为所求Q点,过点A作 MN⊥x轴,分别过点F、D作MN的垂线,垂足分别为点M、N, 则△AND≌△FMA,
由点A、D坐标可得AN=3, DN=6, ∴AM=6, MF=3,∴点F坐标为(1,6), ∴直线DF解析式为: y=-3x+9,∴点Q坐标为(0, 9);
同理, 当点Q在y轴负半轴上时, 构造△APD≌△GHA,可得点G坐标为(-5, - 6), ∴DG解析式为 ∴点Q坐标为
综上, 点Q坐标为(0, 9) 或
7.解析:(1) 设抛物线解析式为y=a(x+1)(x-4),解得: 代入得:
(2) 过点C作CD⊥BC交旋转后的直线与点D,
过点D 作DH⊥y轴交y轴于点 H, 则△DHC≌△COB,
∵OB=4, OC=2, ∴CH=4, DH=2, ∴点D坐标为(2, 6),
∴直线BE的解析式为y=-3x+12,
联立方程: 解得: 将x=5代入抛物线解析式得:y=-3,
∴点E坐标为(5, - 3),
∴BE的长为
第1节 坐标系中的特殊角
前言:坐标系中关于角的探究形式多样,从最基础的角的认识开始,本节讨论关于特殊角的相关内容,从特殊到一般,发现总结关于角处理的常规方法.
知识导航
什么是特殊角
说到特殊角我们很快就能想到比如30°、45°、60°、90°等,事实上,之所以以上角能称为特殊角,关键在于这些角的三角函数值特殊,比如同为整十,为什么我们会将 60°称为特殊角,而50°便不是,原因很简单, 而我们并不知道50°的三角函数值.
因此角度特殊不在于这个角是多少度,而在于其三角函数值是否有特殊值,所以除了常见的 30°、45°、60°,我们可以扩充一下特殊角的范围.
(1) 一组特殊角α与β
引例1:如图所示的网格是正方形网格,则∠PAB+∠PBA= °. (点A、B、P是网格线交点).
解析: 如图, ∠PAB+∠PBA=∠BPQ=45°
(2) 2α与2β的三角函数值
引例2 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片 OABC 沿 OB 折叠, 使点 A 落在点A'的位置, 若 则点A'的坐标为 .
解析: 即△A'HB三边之比为3:4:5,又BA'=BA=2,过点A'作A'H⊥AB 交AB 于点 H, ∴点A'坐标为
中小学教育资源及组卷应用平台
(3) 余角的三角函数值
引例3:在如图的正方形方格纸上,每个小的四边形都是相同的正方形,A、B、C、D都在格点处,AB与CD相交于O, 则tan∠BOD 的值等于 .
解析: 取点E如图所示, 则∠OAE=α, ∠OEA=45°,∠BOD=α+45°, ∴tan∠BOD=3
注意:以上结论不可直接应用于解答题.
2 特殊角与k
坐标系中的直线的“k”与直线和x轴夹角存在某种关系,比如: 45°夹角 |k|=1.
比如: 30°夹角 夹角
一般结论
|k|=tanα (α是直线与x轴的夹角).
k=tanα
k=-tanα
(1) 坐标系中的
(2) 坐标系中的
引例4:如图,在平面直角坐标系中,一次函数y=2x-1的图像分别交x、y轴于点A、B, 将直线AB绕点 B 顺时针旋转 45°,交x轴于点 C,则直线 BC的函数表达式是 .
解析:根据解析式可知
∵OB=1, ∴OC=3, ∴直线BC解析式为
特殊角的构造
在坐标系中构造定角,从其三角函数值着手:
思路1:构造三垂直相似(或全等);
思路2:通过三角函数值化“角度条件”为“直线k”.
引例5:如图,在平面直线坐标系中,直线AB 解析式为 点M(2, 1) 是直线AB上一点, 将直线AB绕点M顺时针旋转45°得到直线 CD,则 CD解析式是 .
思路1:构造三垂直全等(或相似)
过点O作OP⊥AB交 CD于 P 点, 分别过 M、P向x轴作垂线, 垂足为E、F点.
可得: △OEM≌△PFO,
∴PF=OE=2, OF=ME=1, 故P 点坐标为(-1, 2),
结合P、M坐标可解直线 CD解析式:
思路2:利用特殊角的三角函数值.
过M点作MN∥x轴,
则
直线CD的增减性为y随着x的增大而减小,故 ∴CD解析式: 化简得:
45°角的构造
引例6: 如图, 抛物线 过点A (3, 2), 且与直线 交于B、C两点, 点B的坐标为(4, m).
(1) 求抛物线的解析式;
(2) 设点 M为抛物线的顶点,在y轴上是否存在点 Q,使∠AQM=45° 若存在,求点Q的坐标; 若不存在,请说明理由.
解析: (1) 抛物线:
(2) 思路1: 构造三垂直.
如图, AN⊥AQ交直线QM于N点,△ANQ 即为等腰直角三角形,设Q点坐标为(0, m), 又M点坐标为(1, 4),
可得直线QM解析式为: y=(4-m)x+m,
如上右图构造三垂直全等: △QEA≌△AFN,可得: AF=QE=3, NF=AE=2-m,
∴N点坐标为(m+1,5),
将点N代入直线QM解析式: (4-m)(m+1)+m=5,
解得:
∴Q点坐标为( 或((0,2- ).
思路2:圆周角定理
已知点A (3, 2), 可得M点坐标为(1, 4),
过点A作AP 垂直对称轴交对称轴于 P 点,
则△APM是等腰直角三角形, 其中∠APM=90°.
构造∠AQM=45°, 即
如下图,以点 P 为圆心,PA 为半径作圆,与y 轴交点即为所求Q点.
考虑半径 PA=2, 则 PQ=2, 又点 P 在对称轴x=1 上, 点 Q在y轴上,不难求得Q点坐标为(0,2+ )或(0,2- ).
思路概括
关于45°角的构造,常见思路有:
(1) 构造等腰直角三角形,通过三垂直全等计算;
(2) 构造辅助圆,由90°圆心角可得45°圆周角.
真 题 演 练
1. 如图,在平面直角坐标系xOy中,直线y=-x+m分别交x轴、y轴于 A、B 两点, 已知点 C (2,0), 点 P 为线段 OB的中点, 连接 PA、PC, 若∠CPA=∠ABO, 则 m 的值是
2. 如图, 在矩形ABCD中, BC=8, CD=6,将△ABE沿BE 折叠, 使点A 恰好落在对角线 BD 上F处,则DE的长是( )
A. 3 B. C.5
3. 在正方形 ABCD 中, 边长为 6, BE=2AE, 连接 DE, 在AD、BC上分别存在点 G、F, 连接GF交 DE于H点, 且∠GHD=45°, 求线段 FG= .
4. 如图, 直线y=x-3与坐标轴交于A、B两点,抛物线 经过点 B, 与直线y=x-3交于点E (8, 5), 且与x轴交于C, D两点.
(1) 求抛物线的解析式;
(2)抛物线上有一点 M, 当∠MBE=75°时, 求点 M横坐标.
5. 如图, 在平面直角坐标系中, Rt△ABC的斜边AB在x轴上, 点 C在y轴上, ∠ACB=90°, OA、OB 的长分别是一元二次方程 的两个根(OA
(2)连接AD,当AD平分∠CAB时,求直线AD的解析式.
6. 如图, 抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点 C,直线l与抛物线交于A、D两点,与y轴交于点E,点D 的坐标为(4, - 3).
(1) 请直接写出A、B两点的坐标及直线l的函数表达式;
(2) 若点Q是y轴上的点, 且∠ADQ=45°, 求点 Q 的坐标.
7. 如图, 抛物线 经过点A(-1, 0)、B(4, 0), 交y轴于点 C.
(1) 求抛物线的解析式;
(2) 将直线BC绕点 B顺时针旋转45°,与抛物线交于另一点E, 求BE的长.
第1节 坐标系中的特殊角
1.解析:∠PAO=α,∠APC=45°,∴∠OPC=β,∴OP=6,OA=12,m=12.
2.C.
考虑 故选C.
3.解析:观察发现 且∠GHD=45°,考虑 GF可动, 平移GH, 将α、β、45°汇于直角处,可知
4.解析: (1) 抛物线:
(2)①当M点在直线BE上方时,如下左图,若∠MBE=75°,考虑到∠OBE=45°,
则∠OBM=30°, 即直线BM与x轴的夹角为60°,
又B点坐标为(0,-3),∴直线BM的解析式为:
联立方程:
解得: (舍),
∴M点的横坐标为
②当 M 点在直线 BE 下方时, 如上右图, 过点 B 作 BF∥x轴, 则∠EBF=45°, 若∠MBE=75°, 则∠MBF=30°,∴直线BM与x轴夹角为30°, 又B 点坐标为(0, - 3),
故直线BM解析式为:
联立方程:
解得: (舍), ∴M点横坐标为 综上所述,M点横坐标为 或
5.解析: (1) C段坐标为 (0, 12);
(2) 已知直线 AD 上的点 A 坐标,∴求出点 D 坐标或者求出直线的k,即可求出直线AD的解析式.
思路1: 求D点.
易证△ACD≌△AED,∴AC=AE,CD=ED,设ED=x,则CD=x,BD=20-x, 又BE=10, 可得方程:
解得: 故D点坐标为(6,
直线AD解析式为:
思路2: 求k.
易得:
(需证明)
∴直线AD解析式为:
6.解析:: (1)A(-2, 0)、B(6, 0),
直线l的解析式为
(2)当点Q在y轴正半轴上时,如下左图,过点A作AF⊥AD且AF=AD, 连接DF, 与y轴交点即为所求Q点,过点A作 MN⊥x轴,分别过点F、D作MN的垂线,垂足分别为点M、N, 则△AND≌△FMA,
由点A、D坐标可得AN=3, DN=6, ∴AM=6, MF=3,∴点F坐标为(1,6), ∴直线DF解析式为: y=-3x+9,∴点Q坐标为(0, 9);
同理, 当点Q在y轴负半轴上时, 构造△APD≌△GHA,可得点G坐标为(-5, - 6), ∴DG解析式为 ∴点Q坐标为
综上, 点Q坐标为(0, 9) 或
7.解析:(1) 设抛物线解析式为y=a(x+1)(x-4),解得: 代入得:
(2) 过点C作CD⊥BC交旋转后的直线与点D,
过点D 作DH⊥y轴交y轴于点 H, 则△DHC≌△COB,
∵OB=4, OC=2, ∴CH=4, DH=2, ∴点D坐标为(2, 6),
∴直线BE的解析式为y=-3x+12,
联立方程: 解得: 将x=5代入抛物线解析式得:y=-3,
∴点E坐标为(5, - 3),
∴BE的长为
同课章节目录
