新人教版七年级数学上名师点拨与训练第6章几何图形6.2.2线段的比较与运算
文档属性
| 名称 | 新人教版七年级数学上名师点拨与训练第6章几何图形6.2.2线段的比较与运算 |  | |
| 格式 | doc | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 11:37:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
新人教版七年级数学上名师点拨与训练
第6章 几何图形
6.2.2线段的比较与运算
学习目标
1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.
2. 理解线段等分点的意义. 能够运用线段的和、差、倍、分关系求线段的长度.
3 .理解线段的性质,会利用线段性质解释实际问题.
4 .理解两点间的距离概念
重点:会比较两条线段的长短,会利用线段的和、差、倍、分求线段的长度
难点:简单的推理求线段的长度
老师告诉你
1.线段的和差画法注意
画线段的和、差时,均在一条射线上操作,前一条线段的终点是后一条线段的起点,若两条线段的方向相同,则表示它们的和,若两条线段的方向相反,则表示它们的差。
2.线段的中点一定在这条线段上。
知识点拨
知识点1 、线段大小比较
比较线段大小的方法:(1)目测法;(2)度量法;(3)叠合法
叠合比较法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.如下图:
注意:线段的比较方法除了叠合比较法外,度量比较法也是常用的方法.
【新知导学】
例1-1 .如图,AB=CD,那么AC与BD的大小关系是( )
A.AC=BD B.AC<BD C.AC>BD D.不能确定
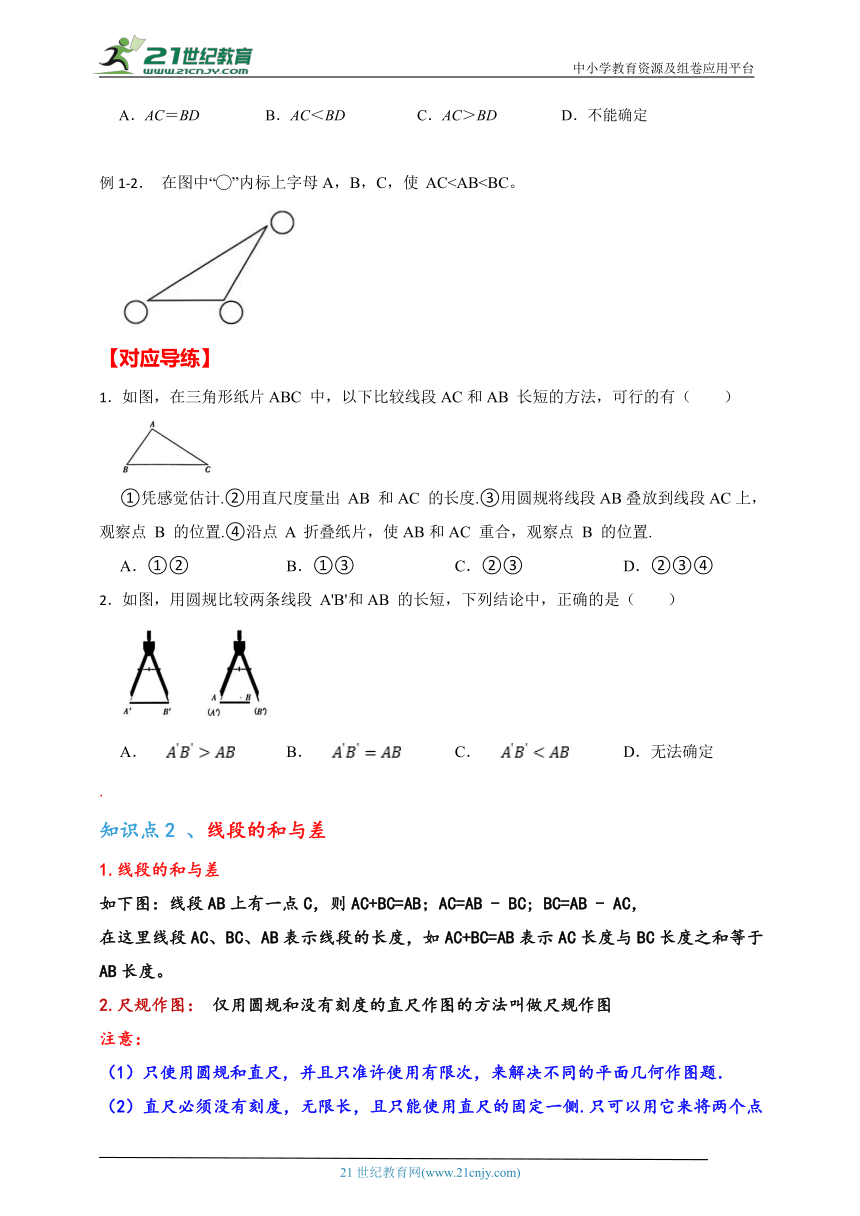
例1-2. 在图中“ ”内标上字母A,B,C,使 AC【对应导练】
1.如图,在三角形纸片ABC 中,以下比较线段AC和AB 长短的方法,可行的有( )
①凭感觉估计.②用直尺度量出 AB 和AC 的长度.③用圆规将线段AB叠放到线段AC上,观察点 B 的位置.④沿点 A 折叠纸片,使AB和AC 重合,观察点 B 的位置.
A.①② B.①③ C.②③ D.②③④
2.如图,用圆规比较两条线段 A'B'和AB 的长短,下列结论中,正确的是( )
A. B. C. D.无法确定
.
知识点2 、线段的和与差
1.线段的和与差
如下图:线段AB上有一点C,则AC+BC=AB;AC=AB - BC; BC=AB - AC,
在这里线段AC、BC、AB表示线段的长度,如AC+BC=AB表示AC长度与BC长度之和等于AB长度。
2.尺规作图: 仅用圆规和没有刻度的直尺作图的方法叫做尺规作图
注意:
(1)只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.
(2)直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上面画刻度.
(3)圆规可以开至无限宽,但上面也不能有刻度.它只可以拉开成之前构造过的长度.
2.作一条线段等于已知线段
“作一条线段等于已知线段”的两种方法:
【方法一】尺规作图:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC上截取AB=a,则线段AB为所求;这是考试中常考点。
【方法二】度量作图:用刻度尺作一条线段等于已知线段.例如:可以先量出线段a的长度,再画一条等于这个长度的线段.
【新知导学】
例2-1. 尺规作图:已知线段 a,b,c(b>c),如图所示.
求作:一条线段,使它等于a+b-c.
解:作法:⑴如图,画射线AE;
⑵在射线AE上顺次截取AC,CD,使 AC= ,CD= ;
⑶在线段AD上截取线段DB,使DB = .
线段 为所求作的线段.
例2-2. 用直尺和圆规作一条线段,使它等于已知线段(要求保留作图痕迹)。
已知:线段a。
求作:线段AB,使AB=a。
【对应导练】
1. 如图,已知线段a,b(a>b),画一条线段x,使x=2a+b.
2.用“>”“<”或“=”填空:
(1)如果点 C 在线段 AB 上,那么 AC AB,AB BC.
(2)如果点 D 在线段AB 的延长线上,那么 AD AB,BD AD.
(3)如果点 E 在线段AB 的反向延长线上,那么 BE AE.
知识点3 、线段性质
线段的基本性质:两点的所有连线中,线段最短.简记为:两点之间,线段最短.
如图所示,在A,B两点所连的线中,线段AB的长度是最短的.
两点间的距离:连接两点间的线段的长度,叫做这两点的距离.
注意:两点的距离是指两点间线段的长度,不是两点间的线段。是一个具体的数值.
【新知导学】
例3-1.关于两点之间的线段,下列说法中不正确的是( )
A.连结两点的线段可以有无数条
B.如果线段AB=AC,那么点A与点B的距离等于点A与点C的距离
C.连结两点的线段的长度是两点间的距离
D.连结两点的线段是连结两点的所有的线中,长度最小的
例3-2.下列现象中,可用基本事实“两点之间线段最短”来解释的是( )
A.用两个钉子就可以把木条固定在墙上
B.利用圆规可以比较两条线段的大小关系
C.把弯曲的公路改直,就能缩短路程
D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
【对应导练】
1.下列说法:(1)在所有连结两点的线中,线段最短;(2)连接两点的线段叫做这两点的距离;(3)若线段 ,则点 是线段 的中点;(4)经过刨平的木板上的两个点,能弹出一条笔直的墨线,是因为两点确定一条直线,其中说法正确的是 ( )
A.(1)(2)(3) B.(1)(4)
C.(2)(3) D.(1)(2)(4)
2.下列说法中,正确的是( )
A.射线是直线的一半
B.线段AB是点A与点B的距离
C.两点之间所有连线中,线段最短
D.角的大小与角的两边所画的长短有关
3.下列说法:①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若α=29°45′,则α的补角是150°55′;⑤若AB=BC,则点B是线段AC的中点.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法:(1)两点之间的所有连线中,线段最短;(2)角是由两条具有公共端点的射线组成的;(3)经过两点有且只有一条直线;(4)连接两点的线段叫做这两点之间的距离.其中正确的有 (填正确说法的序号).
知识点4、 线段的中点
线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如图6所示,点C是线段AB的中点,则,或AB=2AC=2BC.
注意:若点C是线段AB的中点,则点C一定在线段AB上
【新知导学】
例4-1.如图,点是线段的中点,点是线段的中点,点是线段的中点,点是线段的中点.若,则 ;若,则 (用含的代数式表示).
例4-2.如图,D,E顺次为线段AB 上的两点,AB=20,C为AD 的中点,则下列选项正确的是( )
A.若BE-DE=0,则AE-CD=7 B.若BE-DE=2,则AE-CD=7
C.若BE-DE=4,则AE-CD=7 D.若BE-DE=6,则AE-CD=7
【对应导练】
1. 如图,B是线段AC上一点,且
(1)试求出线段AC的长;
(2)如果O是线段AC的中点,请求出线段OB的长.
2.如图,点C 在线段AB 上,AC=2BC,点 D在点E 的左侧。已知AB=18,DE=8,线段DE 在线段AB 上移动。
(1)当 E 为BC 的中点时,求AD 的长。
(2)若点 F(异于点A,B,C)在线段AB 上,AF=3AD,CE+EF=3,求AD 的长。
二、题型训练
1.线段的和差作图
1.用无刻度的直尺和圆规作一条线段,使它等于已知线段.
已知:线段a和线段AB(如图).
求作:延长线段AB至点C,使BC=2a(用直尺和圆规作图,不写作法,保留作图痕迹).
2. 如图,已知线段a,b,c,用圆规和直尺作一条线段,使它等于a+2b-c.
3.如图,已知平面上四个点,请按要求完成下列问题:
(1)画直线,射线,连接;
(2)在射线上作点,使得(尺规作图,保留作图浪迹);
(3)请在直线上确定一点,使最小,画出点,此画图依据是_▲_.
2.利用线段和差计算
4.(1)如图,已知线段a,b,作一条线段,使它等于a+2b.
(2)点M, N, P 在同一条直线上, MN=3cm, NP=1cm.求线段MP 的长.
5.如图,点C是线段的中点.
(1)尺规作图:在线段的延长线上作线段,使得;
(2)若(1)中的线段,求线段的长;并任选三条线段,求出它们的长度和.
6.如图,已知长度为a、b(a>b)的两条线段及射线AH.
(1)尺规作图:在射线AH上作线段AC=2a﹣b,其中AB=2a,BC=b(保留作图痕迹,不写作法);
(2)在(1)的条件下,当a=6cm、b=4cm时,若点M、N分别是线段AC、BC的中点,求线段MN的长度.
3.利用线段中点推理计算
7.如图,AB=18,C为AB 的中点,点D 在线段AC上,且AD:CB=1:3,则 DB 的长为( )
A.8 B.10 C.12 D.15
8.已知线段 ,在直线AB 上有一点C,且 D 是线段AC 的中点,求线段AD 的长.
9.如图,已知A,B,C 是数轴上的三点,O是原点,点C 表示的数为6,BC=4,AB=12。
(1)写出数轴上点 A,B表示的数。
(2)动点 P,Q分别从点A,C同时出发,点P 以每秒6个单位长度的速度沿数轴向右匀速运动,点Q 以每秒3个单位长度的速度沿数轴向左匀速运动,M为AP 的中点,点 N 在线段CQ 上,且 设运动时间为t(s)(t>0)。
①求数轴上点 M,N表示的数(用含 t 的式子表示)。
②当t 为何值时,原点O 恰为线段PQ 的中点
三、课堂达标
一、选择题(每小题4分,共32分)
1. 七年级一班的同学想举行一次拔河比赛,他们想从两条大绳子中挑出一条最长的绳子,同学们说出了几种方法,请你帮他们选择一种最合适的方法 ( )
A.把两条绳子接在一起
B.把两条绳子重合,观察另一端情况
C.把两条大绳的一端对齐,然后同一方向上拉直两条绳子,另一端在外面的即为长绳
D.以上几种方法都可以
2.下列说法中不正确的是( )
A.若点C在线段AB的延长线上,则AC>AB
B.若点C在线段AB上,则ACC.若点C在直线AB上,则AC>AB
D.若A,B,C三点不在一条直线上,可能AC=AB
3.已知点C在线段AB上,则下列条件中,不能确定C是线段AB中点的是( )
A.AC=BC B.AB=2BC C.AC+BC=AB D.BC=AB
4.如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
A.2cm B.4cm C.1cm D.6cm
5.如图,线段 CD 在线段AB 上,且CD=2。若线段 AB 的长度值是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段的长度之和可能是( )
A.28 B.29 C.30 D.31
6.若点A、B、C在同一条直线上,线段AB=5厘米,线段BC=2厘米,则线段AC的长为( )
A.7厘米 B.3厘米
C.7厘米或3厘米 D.不确定
7.如图,C是线段AB 的中点,D 是线段AC上的一点,且 若BC=4,则 DC 的长为 ( )
A.1 B. C. D.2
8.如图,线段,动点P从A出发,以的速度沿运动,M为的中点,N为的中点.以下说法正确的是( )
①运动后,; ②的值随着运动时间的改变而改变;③的值不变;
④当时,运动时间为.
A.①② B.②③ C.①②③ D.②③④
二、填空题(每小题4分,共20分)
9.已知线段AB的中点为点C,则线段AC与AB的数量关系为AC= AB.
10. 如图,C,D是AB 的三等分点,E 是线段CD的中点.若CE=2,则AD 的长为 .
11.如图,点C在线段AB上,已知,点D是线段AB的中点,则线段CD的长是 .
12.如图,C为线段上一点,B为的中点,,.则的长是 .
13.如图,B,C 两点把线段MN 分成三部分,且MB :BC:CN=2:3:4,P 是MN 的中点。若PC=2cm,则MN= cm。
三、解答题(每小题8分,共48分)
14.如图,已知A,B,C,D四点在同一直线上,点D在线段上.点C是线段的中点.
(1)若线段,,求线段的长度;
(2)若,且,求线段的长度.
15.如图,已知、、、四点,请按要求作图,并解答.
(1)画直线;
(2)画射线;
(3)连接与射线交于点;
(4)若点是线段的中点,,,求线段MP的长.
16.如图,已知点在线段上.
(1)尺规作图:在线段的延长线上确定一点,使得;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若点是线段的中点,且,,求的长.
17.如图,已知不在同一直线上的三点A,B,C.
(1)按下面的要求用尺规作图:连接AB,AC,作射线BC;在射线BC上取一点D,使CD=AB.
(2)用刻度尺在(1)的图中画出BC的中点M.若BC=6,AB=8,求MD的长.
18. 阅读下面材料:
在数轴上2与-1所对应的两点之间的距离为|2-(-1)|=3;
在数轴上-2与3所对应的两点之间的距离为|-2-3|=5;
在数轴上-3与-1所对应的两点之间的距离为|(-1)-(-3)|=2.
归纳:在数轴上点A,B分别表示数a,b,则A,B两点之间的距离AB=|a-b|或|b-a|.
回答下列问题:
(1)数轴上表示数x和1的两点之间的距离表示为 ;数轴上表示数x和 的两点之间的距离表示为|x+2|;
(2)试说明当表示数x的点在-2与3的对应点之间移动时,|x-3| +|x+2|的值总是一个固定的值,并求出这个固定值.
19.
(1)【问题探究】
如图,点C,D 均在线段AB 上且点C 在点 D 左侧,若AC=BD,CD=6 cm,AB=9 cm,则线段AC 的长为 cm。
(2)【方法迁移】
已知点C,D 均在线段AB 上且点C 在点D 左侧,若AC=BD,CD=a( cm),AB=b( cm)(b>a),则线段AC 的长为 cm(用含a,b 的代数式表示)。
(3)【学以致用】
已知七年级某班共有m人,在本班参加拓展课报名统计时发现,选择围棋课的人数是n(n新人教版七年级数学上名师点拨与训练
第6章 几何图形
6.2.2线段的比较与运算
学习目标
1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.
2. 理解线段等分点的意义. 能够运用线段的和、差、倍、分关系求线段的长度.
3 .理解线段的性质,会利用线段性质解释实际问题.
4 .理解两点间的距离概念
重点:会比较两条线段的长短,会利用线段的和、差、倍、分求线段的长度
难点:简单的推理求线段的长度
老师告诉你
1.线段的和差画法注意
画线段的和、差时,均在一条射线上操作,前一条线段的终点是后一条线段的起点,若两条线段的方向相同,则表示它们的和,若两条线段的方向相反,则表示它们的差。
2.线段的中点一定在这条线段上。
知识点拨
知识点1 、线段大小比较
比较线段大小的方法:(1)目测法;(2)度量法;(3)叠合法
叠合比较法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.如下图:
注意:线段的比较方法除了叠合比较法外,度量比较法也是常用的方法.
【新知导学】
例1-1 .如图,AB=CD,那么AC与BD的大小关系是( )
A.AC=BD B.AC<BD C.AC>BD D.不能确定
【分析】由题意已知AB=CD,根据等式的基本性质,两边都减去BC,等式仍然成立.
【解析】根据题意和图示可知AB=CD,而CB为AB和CD共有线段,故AC=BD.
故选:A.
例1-2. 在图中“ ”内标上字母A,B,C,使 AC【答案】解:如图所示,AC【知识点】线段的长短比较
【解析】【分析】用观察法、叠合法或度量法比较三条线段的长短,并标记,因为AC 最短,BC最长,所以长线段、短线段的公共端点就是点C,然后确定点A,点B的位置.
【对应导练】
1.如图,在三角形纸片ABC 中,以下比较线段AC和AB 长短的方法,可行的有( )
①凭感觉估计.②用直尺度量出 AB 和AC 的长度.③用圆规将线段AB叠放到线段AC上,观察点 B 的位置.④沿点 A 折叠纸片,使AB和AC 重合,观察点 B 的位置.
A.①② B.①③ C.②③ D.②③④
【答案】D
【知识点】线段的长短比较
【解析】【解答】解:① 凭感觉估计 ,不可行,不符合题意;
②用直尺度量出 AB 和AC 的长度 ,通过测量比较,可行,符合题意;
③用圆规将线段AB叠放到线段AC上,观察点 B 的位置,根据点B在AC上还是AC外可比较,可行,符合题意 ;
④沿点 A 折叠纸片,使AB和AC 重合,观察点 B 的位置根据点B在AC上还是AC外可比较,可行,符合题意 .
故答案为:D.
【分析】根据测量法和叠合法比较线段的大小即可判断.
2.如图,用圆规比较两条线段 A'B'和AB 的长短,下列结论中,正确的是( )
A. B. C. D.无法确定
【答案】A
【知识点】线段的长短比较
【解析】【解答】解:
故答案为:A.
【分析】根据 A'B' 中,点A与A'重合,端点 B'在AB的延长线上可得 A'B' >AB.
知识点2 、线段的和与差
1.线段的和与差
如下图:线段AB上有一点C,则AC+BC=AB;AC=AB - BC; BC=AB - AC,
在这里线段AC、BC、AB表示线段的长度,如AC+BC=AB表示AC长度与BC长度之和等于AB长度。
2.尺规作图: 仅用圆规和没有刻度的直尺作图的方法叫做尺规作图
注意:
(1)只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.
(2)直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上面画刻度.
(3)圆规可以开至无限宽,但上面也不能有刻度.它只可以拉开成之前构造过的长度.
2.作一条线段等于已知线段
“作一条线段等于已知线段”的两种方法:
【方法一】尺规作图:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC上截取AB=a,则线段AB为所求;这是考试中常考点。
【方法二】度量作图:用刻度尺作一条线段等于已知线段.例如:可以先量出线段a的长度,再画一条等于这个长度的线段.
【新知导学】
例2-1. 尺规作图:已知线段 a,b,c(b>c),如图所示.
求作:一条线段,使它等于a+b-c.
解:作法:⑴如图,画射线AE;
⑵在射线AE上顺次截取AC,CD,使 AC= ,CD= ;
⑶在线段AD上截取线段DB,使DB = .
线段 为所求作的线段.
【答案】a;b;c;AB
【知识点】尺规作图-线段的和差
【解析】【解答】解:作法:⑴如图,画射线AE;
⑵在射线AE上顺次截取AC,CD,使 AC=a,CD=b,
⑶在线段AD上截取线段DB,使DB =c,
线段AB为所求作的线段.
故答案为:a,b,c,AB.
【分析】利用线段定义及作图方法作出图形即可.
例2-2. 用直尺和圆规作一条线段,使它等于已知线段(要求保留作图痕迹)。
已知:线段a。
求作:线段AB,使AB=a。
【答案】解:如图所示。
【知识点】尺规作图-线段的和差
【解析】【分析】首先画射线,然后再用圆规在射线上截取AB=a即可.
【对应导练】
1. 如图,已知线段a,b(a>b),画一条线段x,使x=2a+b.
【答案】解:如图所示:
(1)作射线OP,
(2)在射线OP上截取OA=a,AB=a,BC=b,线段OC就是所要画的线段.
【知识点】尺规作图-线段的和差
【解析】【分析】先作出射线,再在这条射线上截取2段长度等于a的线段和一段长度等于b的线段即可.
2.用“>”“<”或“=”填空:
(1)如果点 C 在线段 AB 上,那么 AC AB,AB BC.
(2)如果点 D 在线段AB 的延长线上,那么 AD AB,BD AD.
(3)如果点 E 在线段AB 的反向延长线上,那么 BE AE.
【答案】(1)<;>
(2)>;<
(3)>
【知识点】线段的长短比较
【解析】【解答】解:(1)如图.
ACBC;
故答案为:<,>.
(2)如图.
AD>AB,BD故答案为:>,<.
(3)如图.
BE>AE.
故答案为:>.
【分析】(1)画出图形,再比较AC与AB的大小,比较AB与BC的大小;
(2)画出图形,再比较AD与AB的大小,BD与AD的大小;
(3)画出图形,再比较BE与AE的大小.
知识点3 、线段性质
线段的基本性质:两点的所有连线中,线段最短.简记为:两点之间,线段最短.
如图所示,在A,B两点所连的线中,线段AB的长度是最短的.
两点间的距离:连接两点间的线段的长度,叫做这两点的距离.
注意:两点的距离是指两点间线段的长度,不是两点间的线段。是一个具体的数值.
【新知导学】
例3-1.关于两点之间的线段,下列说法中不正确的是( )
A.连结两点的线段可以有无数条
B.如果线段AB=AC,那么点A与点B的距离等于点A与点C的距离
C.连结两点的线段的长度是两点间的距离
D.连结两点的线段是连结两点的所有的线中,长度最小的
【答案】A
【知识点】线段上的两点间的距离
【解析】【解答】 A、连接两点的线段只有1条,故A错误;
B、线段AB=AC,那么点A与点B的距离等于点A与点C的距离,故B正确;
C、连接两点的线段的长度,是两点间的距离,故C正确;
D、两点之间的距离是连接两点的所有线的长度中,长度最短的,故D正确;
故答案为:A.
【分析】根据两点之间距离、线段的基本事实求解.
例3-2.下列现象中,可用基本事实“两点之间线段最短”来解释的是( )
A.用两个钉子就可以把木条固定在墙上
B.利用圆规可以比较两条线段的大小关系
C.把弯曲的公路改直,就能缩短路程
D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
【答案】C
【知识点】两点确定一条直线;两点之间线段最短;线段的长短比较
【解析】【解答】解:A、用两个钉子就可以把木条固定在墙上,是两点确定一条直线,A错误;
B、利用圆规可以比较两条线段的大小关系,是线段长度比较,B错误;
C、把弯曲的公路改直,就能缩短路程,可用基本事实“两点之间,线段最短”来解释,C正确;
D、植树时,只要定出两棵树的位置,就能确定同一行树所在的直线,是两点确定一条直线,D错误;
故答案为:C.
【分析】根据两点确定一条直线可判断A和D选项说法不符合题意;根据用圆规来比较线段的大小可判断B选项不符合题意;根据两点之间,线段最短可判断C选项说法符合题意;即可得出答案.
【对应导练】
1.下列说法:(1)在所有连结两点的线中,线段最短;(2)连接两点的线段叫做这两点的距离;(3)若线段 ,则点 是线段 的中点;(4)经过刨平的木板上的两个点,能弹出一条笔直的墨线,是因为两点确定一条直线,其中说法正确的是 ( )
A.(1)(2)(3) B.(1)(4)
C.(2)(3) D.(1)(2)(4)
【答案】B
【知识点】两点确定一条直线;两点之间线段最短;线段上的两点间的距离;线段的中点
【解析】【解答】解:(1)在所有连结两点的线中,线段最短,故原说法正确;
(2)连接两点的线段的长度叫做这两点的距离,故原说法错误;
(3)若线段AC=BC,且当点C在线段AB上时,点C才是线段AB的中点,故原说法错误;
(4)经过刨平的木板上的两个点,能弹出一条笔直的墨线,是因为两点确定一条直线,故原说法正确;
综上所述,说法正确有(1)(4).
故答案为:B.
【分析】根据两点之间线段最短的性质判断 (1);根据数轴上两点间的距离的定义判断(2);根据线段的中点的定义判断(3);根据直线的性质判断(4).
2.下列说法中,正确的是( )
A.射线是直线的一半
B.线段AB是点A与点B的距离
C.两点之间所有连线中,线段最短
D.角的大小与角的两边所画的长短有关
【答案】C
【知识点】直线、射线、线段;两点之间线段最短;线段上的两点间的距离;角的概念及表示
【解析】【解答】解:A、射线的长度无法度量,故不是直线的一半,故本选项错误;
B、线段AB的长度是点A与点B的距离,故本选项错误;
C、两点之间所有连线中,线段最短,故本选项正确;
D、角的大小与角的两边所画的长短无关,故本选项错误.
故答案为:C.
【分析】根据射线、直线、线段及角的概念、两点间的距离、线段的性质逐一分析并判断即可.
3.下列说法:①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若α=29°45′,则α的补角是150°55′;⑤若AB=BC,则点B是线段AC的中点.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【知识点】两点确定一条直线;两点之间线段最短;线段上的两点间的距离;余角、补角及其性质;线段的中点
【解析】【解答】解:①是直线的公理,故本选项正确;
②连接两点的线段的长度叫两点的距离,故本选项错误;
③是线段的性质,故本选项正确;
④若α=29°45′,则α的补角是150°15′,故本选项错误;
⑤A、B、C可能不共线,故本选项错误.
故答案为:B.
【分析】根据直线公理可判断①;距离是长度,线段是图形,故连接两点的线段的长度才叫两点的距离,据此判断②;根据线段公理判断③;和为180°的两个角互为补角,据此判断④;A、B、C可能不在同一直线上,也可能在同一条直线上,只有当三点在同一直线上的时候,点B才是线段AC的中点,据此可判断⑤.
4.下列说法:(1)两点之间的所有连线中,线段最短;(2)角是由两条具有公共端点的射线组成的;(3)经过两点有且只有一条直线;(4)连接两点的线段叫做这两点之间的距离.其中正确的有 (填正确说法的序号).
【答案】(1)(2)(3)
【知识点】两点确定一条直线;两点之间线段最短;线段上的两点间的距离;角的概念及表示
【解析】【解答】解:(1)两点之间的所有连线中,线段最短,正确;
(2)角是由两条具有公共端点的射线组成的,正确;
(3)经过两点有且只有一条直线,正确;
(4)连接两点的线段的长度叫做这两点之间的距离,故原说法错误.
故答案为:(1)(2)(3).
【分析】根据两点之间,线段最短的性质可判断(1);根据角的概念可判断(2);根据直线的概念可判断(3);根据两点间距离的概念可判断(4).
知识点4、 线段的中点
线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如图6所示,点C是线段AB的中点,则,或AB=2AC=2BC.
注意:若点C是线段AB的中点,则点C一定在线段AB上
【新知导学】
例4-1.如图,点是线段的中点,点是线段的中点,点是线段的中点,点是线段的中点.若,则 ;若,则 (用含的代数式表示).
【答案】0.5;
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵AB=8,点O是线段AB的中点,
∴OA=OB=AB=4,
∵点D是线段AO的中点,
∴AD=AO=2,BD=8 2=6,
∵点E是线段BD的中点,
∴BE=DE=3,AE=8 3=5,
∵点F是线段AE的中点,
∴AF=AE=2.5,
∴DF=AF AD=2.5 2=0.5;
设OA=OB=x,则AB=2x,BE=x a,
∵点E是线段BD的中点,
∴BD=2BE=2x 2a,
∵点D是线段AO的中点,
∴AD=AO=x,
∴AB=AD+BD=x+2x 2a=x 2a,
∴OB=AB=x a,即x a=x,
解得x=4a,
即AE=AO+OE=x+a=5a,
∵点F是线段AE的中点,
∴EF=AE=a,
∴OF=EF OE=a a=a.
故答案为:0.5;a.
【分析】根据中点的概念可得OA=OB=AB=4,AD=AO=2,则BD=AB-AD=6,同理可得BE=DE=3,AE=5,AF=AE=2.5,DF=AF-AD=0.5,设OA=OB=x,则AB=2x,BE=x-a,由中点的概念可得BD=2BE=2x-2a,AD=AO=x,则AB=AD+BD=x 2a,OB=AB=x a,结合OB=4可得x=4a,则AE=AO+OE=5a,EF=AE=a,然后根据OF=EF-OE进行计算.
例4-2.如图,D,E顺次为线段AB 上的两点,AB=20,C为AD 的中点,则下列选项正确的是( )
A.若BE-DE=0,则AE-CD=7 B.若BE-DE=2,则AE-CD=7
C.若BE-DE=4,则AE-CD=7 D.若BE-DE=6,则AE-CD=7
【答案】D
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:由 BE-DE=0,可设DE=x,则BE=x,
∴AD=20-x-x=20-2x,
∵C为AD 的中点,
∴AC=CD=10-x,AE=20-2x+x=20-x,
∴AE-CD=(20-x)-(10-x)=10,故A错误;
由 BE-DE=2,可设DE=x,则 BE=x+2,
∴AD=20-x-(x+2)=18-2x,
∵C为AD 的中点,
∴AC=CD=9-x,AE=18-2x+x=18-x,
∴AE-CD=(18-x)-(9-x)=9,故B错误;
由BE-DE=4,可设DE=x,则 BE=x+4,
∴AD=20-x-(x+4)=16-2x,
∵C为AD的中点,
∴AC=CD=8-x,AE=16-2x+x=16-x,
∴AE-CD=(16-x)-(8-x)=8,故C错误;
由BE-DE=6,可设DE=x,则BE=x+6,
∴AD=20-x-(x+6)=14-2x,
∵C为AD的中点,
∴AC=CD=7-x,AE=14-2x+x=14-x,
∴AE-CD=(14-x)-(7-x)=7,故D正确。
故答案为:D.
【分析】根据线段中点的定义与线段的和差逐项分析可得答案.
【对应导练】
1. 如图,B是线段AC上一点,且
(1)试求出线段AC的长;
(2)如果O是线段AC的中点,请求出线段OB的长.
【答案】(1)解:∵AB=21cm,BC=AB,
∴BC=×21=7(cm),
∴AC=AB+BC=21+7=28(cm).
(2)解:∵O是线段AC的中点,
∴OC=AC=14cm,
∴OB=OC BC=14 7=7(cm).
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】(1)根据“BC=AB”求出BC的长,再利用线段的和差求出AC的长即可;
(2)先利用线段中点的性质求出OC的长,再利用线段的和差求出OB的长即可.
2.如图,点C 在线段AB 上,AC=2BC,点 D在点E 的左侧。已知AB=18,DE=8,线段DE 在线段AB 上移动。
(1)当 E 为BC 的中点时,求AD 的长。
(2)若点 F(异于点A,B,C)在线段AB 上,AF=3AD,CE+EF=3,求AD 的长。
【答案】(1)解:∵,,,
∴,,
如图,
∵E为BC中点,
∴,
∴,
∴;
(2)解:由题意,得AF=3AD,AE=AD+DE=AD+8,
分类讨论:
①如图,当点E在点F的左侧时,
∵,,
∴,,
∵,,
∴点F是BC的中点,
∴,
∴,
∴;
②如图,当点E在点F的右侧,
∵,,
∴,
∴,
∴.
综上所述:AD的长为3或5;
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】(1)由,,可求出,.再根据E为BC中点,即得出,从而可求出CD的长,进而可求出AD的长;
(2)分类讨论:当点E在点F的左侧时和当点E在点F的右侧时,画出图形,根据线段的倍数关系和和差关系,利用数形结合的思想即可解题.
二、题型训练
1.线段的和差作图
1.用无刻度的直尺和圆规作一条线段,使它等于已知线段.
已知:线段a和线段AB(如图).
求作:延长线段AB至点C,使BC=2a(用直尺和圆规作图,不写作法,保留作图痕迹).
【答案】解:如图:
【知识点】尺规作图-线段的和差
【解析】【分析】根据尺规作图步骤:延长AB,以点B为圆心,a为半径做弧,交延长线于点D,再以点D为圆心,a为半径做弧,交延长线于点C,即为所求.
2. 如图,已知线段a,b,c,用圆规和直尺作一条线段,使它等于a+2b-c.
【答案】解:如图:AE=a+2b-c即为所求:
作图步骤如下:
①作射线AM;
②在射线AM上依次截取AB=a,BC=CD=b;
③在线段AD上截取DE=c;
④则线段AE=AB+BC+CD-DE=a+2b-c;
线段AE即可为所求.
【知识点】尺规作图-线段的和差
【解析】【分析】①作射线AM;②在射线AM上依次截取AB=a,BC=CD=b;③在线段AD上截取DE=c;④则线段AE=AB+BC+CD-DE=a+2b-c;线段AE即可为所求.
3.如图,已知平面上四个点,请按要求完成下列问题:
(1)画直线,射线,连接;
(2)在射线上作点,使得(尺规作图,保留作图浪迹);
(3)请在直线上确定一点,使最小,画出点,此画图依据是_▲_.
【答案】(1)如下图所示:
直线,射线,线段为求作的;
(2)以A为圆心,的长为半径画弧,交射线于点P,如下图所示,
线段为求作图形;
(3)连接,交于点Q,如下图所示:
点Q为求作的点,
依据:两点之间,线段最短.
【知识点】两点之间线段最短;尺规作图-直线、射线、线段;尺规作图-线段的和差
【解析】【分析】(1)根据直线,射线,线段的定义画出图形即可;
(2)以A为圆心,DC为半径作弧,交AB于点P,点P即为所求;
(3)连接PD交AC于点Q,点Q即为所求.
2.利用线段和差计算
4.(1)如图,已知线段a,b,作一条线段,使它等于a+2b.
(2)点M, N, P 在同一条直线上, MN=3cm, NP=1cm.求线段MP 的长.
【答案】解:(1)作射线AM;
在射线AM上依次截取AB=a,BC=CD=b,
则线段AD=a+2b即为所求;
(2)当点P在线段MN上,如图(1)
∵ MN=3cm, NP=1cm ,
∴MN=MN-MP=3-1=2cm.
当点P在线段MN的延长线上,如图(2)
∵ MN=3cm, NP=1cm ,
∴MN=MN+MP=3+1=4cm.
故线段MP的长为2cm或4cm.
【知识点】尺规作图-线段的和差
【解析】【分析】(1)作射线AM;在射线AM上依次截取AB=a,BC=CD=b;则线段AD=a+2b即为所求;
(2)分点P在线段MN上和点P在线段MN的延长线上两种情况作线段的和差运算即可.
5.如图,点C是线段的中点.
(1)尺规作图:在线段的延长线上作线段,使得;
(2)若(1)中的线段,求线段的长;并任选三条线段,求出它们的长度和.
【答案】(1)解:如图,延长线段,以B为圆心为半径画圆弧交延长线于一点即为D点,
(2)解:由(1)得B为的中点,
∵,
∴
∵C为的中点,
∴
∴(答案不唯一).
【知识点】线段的中点;线段的和、差、倍、分的简单计算;尺规作图-线段的和差
【解析】【分析】(1)延长线段,以B为圆心为半径画圆弧交延长线于一点即为D点;
(2)利用线段中点的性质及线段的和差分析求解即可.
6.如图,已知长度为a、b(a>b)的两条线段及射线AH.
(1)尺规作图:在射线AH上作线段AC=2a﹣b,其中AB=2a,BC=b(保留作图痕迹,不写作法);
(2)在(1)的条件下,当a=6cm、b=4cm时,若点M、N分别是线段AC、BC的中点,求线段MN的长度.
【答案】(1)解:如图所示,
(2)解:当、时,,
、分别是线段、的中点
,.
.
【知识点】线段的中点;线段的和、差、倍、分的简单计算;尺规作图-线段的和差
【解析】【分析】(1)以点为圆心,线段的长为半径画弧,交射线于点,再以点为圆心,线段的长为半径画弧,交射线于点,再以点为圆心,线段的长为半径画弧,交线段于点,则线段即为所作图.
(2)由题意可得,,根据中点的定义可求出,,再利用线段运算可得:,代入数据可求出答案.
3.利用线段中点推理计算
7.如图,AB=18,C为AB 的中点,点D 在线段AC上,且AD:CB=1:3,则 DB 的长为( )
A.8 B.10 C.12 D.15
【答案】D
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵,点C为的中点,
∴,
∵,
∴,
∴.
故答案为:D
【分析】根据线段中点的定义可得,再求出,然后根据,代入数据计算即可得解.
8.已知线段 ,在直线AB 上有一点C,且 D 是线段AC 的中点,求线段AD 的长.
【答案】解:分两种情况讨论:
①如图1所示,当点C在点A与B之间时,
∵线段,,
∴,
∵D是线段的中点,
∴;
②当点C在点B的右侧时,如图2所示:
∵线段,,
∴,
∵D是线段的中点,
∴;
综上所述,线段的长为或.
【知识点】线段的中点;线段的和、差、倍、分的简单计算;分类讨论
【解析】【分析】应考虑到A、B、C三点之间的位置关系的多种可能,即点C在点A与B之间或点C在点B的右侧两种情况进行分类讨论.
9.如图,已知A,B,C 是数轴上的三点,O是原点,点C 表示的数为6,BC=4,AB=12。
(1)写出数轴上点 A,B表示的数。
(2)动点 P,Q分别从点A,C同时出发,点P 以每秒6个单位长度的速度沿数轴向右匀速运动,点Q 以每秒3个单位长度的速度沿数轴向左匀速运动,M为AP 的中点,点 N 在线段CQ 上,且 设运动时间为t(s)(t>0)。
①求数轴上点 M,N表示的数(用含 t 的式子表示)。
②当t 为何值时,原点O 恰为线段PQ 的中点
【答案】(1)解:∵点C 表示的数为6,BC=4,
∴OB=6-4=2,
∴点 B 表示的数为2。
∵AB=12,
∴AO=12-2=10,
∴点A 表示的数为-10
(2)解:①由题意可知:AP=6t,CQ=3t。
∵M 为AP 的中点,
∴在数轴上点 M 表示的数是-10+3t。
∵点 N 在CQ上,
∴在数轴上点 N 表示的数是6-t。
②分两种情况讨论:
i.如解图①,当点 P 在点O 的左侧,点Q 在点O的右侧时,。
∵O为PQ 的中点,∴OP=OQ,
∴10-6t=6-3t,解得
ii.如解图②,当点 P 在点O 的右侧,点 Q 在点O 的左侧时,。
∵O为PQ 的中点,∴,
∴,解得 (此时AP=8<10,不合题意,舍去)。
综上所述,当 时,原点O恰为线段PQ 的中点
【知识点】一元一次方程的其他应用;线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】(1)根据数轴上两点间的距离即可求出A、B表示的数;
(2)①根据距离=速度×时间可得AP=6t,CQ=3t,根据中点性质可得AM=3t,根据 可得CN=t,根据线段的和差关系即可得答案;②根据中点定义可得,分两种情况,当点 P 在点O 的左侧,点Q 在点O的右侧时或者当点 P 在点O 的右侧,点 Q 在点O 的左侧时,再根据数轴的性质解答即可.
三、课堂达标
一、选择题(每小题4分,共32分)
1. 七年级一班的同学想举行一次拔河比赛,他们想从两条大绳子中挑出一条最长的绳子,同学们说出了几种方法,请你帮他们选择一种最合适的方法 ( )
A.把两条绳子接在一起
B.把两条绳子重合,观察另一端情况
C.把两条大绳的一端对齐,然后同一方向上拉直两条绳子,另一端在外面的即为长绳
D.以上几种方法都可以
【答案】C
【知识点】线段的长短比较
【解析】【解答】解:利用叠合法,即把两条大绳的一端对齐,然后同一方向上拉直两条绳子,另一端在外面的即为长绳.
故答案为:C.
【分析】利用叠合法判断,判断哪个选项中叠合的步骤正确即可.
2.下列说法中不正确的是( )
A.若点C在线段AB的延长线上,则AC>AB
B.若点C在线段AB上,则ACC.若点C在直线AB上,则AC>AB
D.若A,B,C三点不在一条直线上,可能AC=AB
【答案】C
【知识点】线段的长短比较
【解析】【解答】A.如图, 点C在线段AB的延长线上, AC=AB+BC>AB,即AC>AB,故正确;
B.如图, 若点C在线段AB上, AC=AB-BCC. 点C在直线AB上, 则点C可以在线段AB的延长线上,此时由A知AC>AB,也可以线段AB上,此时由B知ACAB,也可以是ACD.如图, A,B,C三点不在一条直线上,可能AC=AB ,故正确.
故答案为:C.
【分析】分别根据各选项画出图形,再写出式子比较大小,然后判断正确与否,再选出错误的.
3.已知点C在线段AB上,则下列条件中,不能确定C是线段AB中点的是( )
A.AC=BC B.AB=2BC C.AC+BC=AB D.BC=AB
【答案】C
【知识点】线段的中点
【解析】【解答】解:若点C为线段AB中点,
∴
而无论点C在线段AB的任意一位置,
都有:
故答案为:C.
【分析】根据中点的性质,逐项判断即可.
4.如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
A.2cm B.4cm C.1cm D.6cm
【答案】B
【知识点】线段上的两点间的距离
【解析】【解答】解:∵点M是AC的中点,点N是BC的中点,
∴AC=2MC,BC=2NC,
∴AC﹣BC=(MC﹣NC)×2=2×2=4(cm),
即AC比BC长4cm.
故选:B.
【分析】根据点M是AC的中点,点N是BC的中点,可得AC=2MC,BC=2NC,所以AC﹣BC=(MC﹣NC)×2,据此解答即可.
5.如图,线段 CD 在线段AB 上,且CD=2。若线段 AB 的长度值是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段的长度之和可能是( )
A.28 B.29 C.30 D.31
【答案】B
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】以这四点中任意两点为端点的所有线段为:
设,则b为正整数
由图可知,
又
则能够整除3
观察四个选项可知,只有B选项符合要求
故答案为:B.
【分析】先写出以这四点中任意两点为端点的所有线段,从而可得出所求的所有线段之和,再根据线段的和差、整数性判断即可.
6.若点A、B、C在同一条直线上,线段AB=5厘米,线段BC=2厘米,则线段AC的长为( )
A.7厘米 B.3厘米
C.7厘米或3厘米 D.不确定
【答案】C
【知识点】线段的和、差、倍、分的简单计算
【解析】【解答】解:解:当C在线段AB上时:AC=AB-BC=5-2=3(厘米);
当C在AB的延长线上时:AC=AB+BC=5+2=7(厘米);
综上,线段AC的长为7厘米或3厘米.
故答案为:C.
【分析】分两种情况讨论:即C在线段AB上,C在AB的延长线上,分别列式计算即可.
7.如图,C是线段AB 的中点,D 是线段AC上的一点,且 若BC=4,则 DC 的长为 ( )
A.1 B. C. D.2
【答案】A
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵C是AB的中点,BC=4,
∴AC=BC=4,
∵DC=AC,
∴DC=1;
故答案为:A.
【分析】根据线段的中点,可得出AC的长度,再根据DC=AC,即可得出DC的长度.
8.如图,线段,动点P从A出发,以的速度沿运动,M为的中点,N为的中点.以下说法正确的是( )
①运动后,; ②的值随着运动时间的改变而改变;③的值不变;
④当时,运动时间为.
A.①② B.②③ C.①②③ D.②③④
【答案】D
【知识点】线段的中点;一元一次方程的实际应用-行程问题;线段的和、差、倍、分的简单计算
【解析】【解答】解:①运动4s后,AP=2×4=8cm,PB=AB-AP=16cm,
∵M为的中点 ,
∴AM=MP=4cm,
∴PB=4AM,故①错误;
设运动ts时,AP=2t,PB=24-2t,
∵M为的中点,N为的中点,
∴AM=PM=t,PN=BN=12-t,
∴PM+MN=PM+PM+PN=t+t+12-t=12+t,
∴的值随着运动时间的改变而改变 ,故②正确;
∵MB=AB-AM=24-t,PB=AB-AP=24-2t,
∴=2(24-t)-(24-2t)=24cm,故③正确;
由AN=AP+PN=2t+(12-t)=12+t,PM=t,
∵ ,
∴12+t=6t,解得t=2.4s,故④正确.
故答案为:D.
【分析】根据题意分别求出AP、PB的长,再利用线段的中点得出AM、PM、PN、BN的长,利用线段的和差关系逐一求解即可判断.
二、填空题(每小题4分,共20分)
9.已知线段AB的中点为点C,则线段AC与AB的数量关系为AC= AB.
【答案】
【知识点】线段的中点
【解析】【解答】解: ∵线段AB的中点为点C ,
∴AC=BC=AB.
故答案为:.
【分析】根据线段的中点定义进行解答即可.
10. 如图,C,D是AB 的三等分点,E 是线段CD的中点.若CE=2,则AD 的长为 .
【答案】8
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:如∵ C,D是AB 的三等分点
∴AC=CD=AB
∵E 是线段CD的中点.
∴AE=AB
又∵AE-AC=EC
∴AB-AB=2
∴AB=12
∴AC=CD=AB=×12=4
∴AD=AC+CD
=4+4
=8
∴故答案为:8.
【分析】由线段三等分点、中点的定义可知:C=CD=AB,AE=AB,再线段的差关系得到:AB-AB=2,从而求出AB,再用线段的倍数关系可求出:AC=CD=AB,再由线段的和关系:AD=AC+CD即可求解.
11.如图,点C在线段AB上,已知,点D是线段AB的中点,则线段CD的长是 .
【答案】1
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵AB=10,D是线段AB的中点,
∴BD=AB=4,
∵CB=3,
∴CD=DB BC=1,
故答案为:1.
【分析】先利用线段中点的性质求出BD=AB=4,再利用线段的和差求出CD的长即可.
12.如图,C为线段上一点,B为的中点,,.则的长是 .
【答案】
【知识点】线段的中点
【解析】【解答】解:∵B为的中点,
∴,
∴,
故答案为:
【分析】本题考查了与线段中点有关的计算,由B为的中点,得到,结合,进行计算,即可求解.
13.如图,B,C 两点把线段MN 分成三部分,且MB :BC:CN=2:3:4,P 是MN 的中点。若PC=2cm,则MN= cm。
【答案】36
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵,
∴设,
则,
∵点P是的中点,
∴,
∴,
∵,
∴,
解得,
∴.
故答案为:.
【分析】根据线段比例,设设,则,列出一元一次方程求解即可.本题考查两点间的距离,弄清楚线段之间的数量关系是关键.
三、解答题(每小题8分,共48分)
14.如图,已知A,B,C,D四点在同一直线上,点D在线段上.点C是线段的中点.
(1)若线段,,求线段的长度;
(2)若,且,求线段的长度.
【答案】(1)解:∵,点C是线段的中点,
∴,
∵,
∴
(2)解:∵点C是线段的中点,
∴设,
∵,
∴,,
∵,
∴,
解得,
∴
【知识点】线段的中点;一元一次方程的实际应用-几何问题;线段的和、差、倍、分的简单计算
【解析】【分析】(1)先由“ 点C是线段的中点 ”,求出BC的长,在根据“”,可知CD为BC的,即可求出CD长;
(2)通过设未知数x,分别表示出AD和BD的长,在根据条件“ ”,即可列出等式,继而可求出x的值,得到AB的长.
15.如图,已知、、、四点,请按要求作图,并解答.
(1)画直线;
(2)画射线;
(3)连接与射线交于点;
(4)若点是线段的中点,,,求线段MP的长.
【答案】(1)图见解析,直线即为所求;
(2)图见解析,射线即为所求;
(3)图见解析,线段、点即为所求;
(4)∵,
∴DB = DP+BP = 10
∵M是BD中点
∴BM =DB = 5
∴MP = BM-BP = 5-3 = 2
【知识点】线段的中点;尺规作图-直线、射线、线段;线段的和、差、倍、分的简单计算
【解析】【解答】解:(1)如图,直线即为所求;
(2)如图,射线即为所求;
(3)如图,点P即为所求;
【分析】(1)根据直线的定义画图即可;
(2)根据射线的定义画图即可;
(3)根据线段的定义画图即可;
(4)由DB = DP+BP 求出DB的长,再由线段的中的的定义求出BM的长,利用MP = BM-BP即可求解.
16.如图,已知点在线段上.
(1)尺规作图:在线段的延长线上确定一点,使得;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若点是线段的中点,且,,求的长.
【答案】(1)解:∵,
∴点即为所求,
(2)解:∵点是线段的中点,,,
∴,
∴,
∵,
∴,
∴.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】(1)根据题意,以D为圆心,AB长为半径作弧交的延长线于点 ,点即为所求;
(2)根据中点的定义可知, 由,, 计算求解即可得到答案.
17.如图,已知不在同一直线上的三点A,B,C.
(1)按下面的要求用尺规作图:连接AB,AC,作射线BC;在射线BC上取一点D,使CD=AB.
(2)用刻度尺在(1)的图中画出BC的中点M.若BC=6,AB=8,求MD的长.
【答案】(1)解:如图,点D即为所求;
;
(2)解:∵M是BC的中点.∴CM=BC=3,
∵CD=AB=8,
∴MD=CM+CD=3+8=11.
【知识点】线段的中点;尺规作图-直线、射线、线段;线段的和、差、倍、分的简单计算
【解析】【分析】(1)根据线段、射线定义,两点确定一条直线,且由线段的一端无限延长所形成的直的线,有且仅有一个端点,无法测量长度,即可完成作图;
(2)根据线段中点定义,结合CM=BC,求得CM=3,再由MD=CM+CD,进而可得MD的长.
18. 阅读下面材料:
在数轴上2与-1所对应的两点之间的距离为|2-(-1)|=3;
在数轴上-2与3所对应的两点之间的距离为|-2-3|=5;
在数轴上-3与-1所对应的两点之间的距离为|(-1)-(-3)|=2.
归纳:在数轴上点A,B分别表示数a,b,则A,B两点之间的距离AB=|a-b|或|b-a|.
回答下列问题:
(1)数轴上表示数x和1的两点之间的距离表示为 ;数轴上表示数x和 的两点之间的距离表示为|x+2|;
(2)试说明当表示数x的点在-2与3的对应点之间移动时,|x-3| +|x+2|的值总是一个固定的值,并求出这个固定值.
【答案】(1);-2
(2)解:因为-2所以|x-3|+|x+2|
=3-x+x+2
=5.
即当表示数x的点在-2与3的对应点之间移动时,|x-3|+|x+2|的值总是一个固定的值,这个固定值为5.
【知识点】数轴及有理数在数轴上的表示;绝对值及有理数的绝对值;线段上的两点间的距离
【解析】【解答】解:(1) 数轴上表示数x和1的两点之间的距离表示为 ;数轴上表示数x和-2的两点之间的距离表示为|x+2|;
故答案为: ,|x+2|,
【分析】(1)根据两点间的距离公式解答即可;
(2)由题意得-219.
(1)【问题探究】
如图,点C,D 均在线段AB 上且点C 在点 D 左侧,若AC=BD,CD=6 cm,AB=9 cm,则线段AC 的长为 cm。
(2)【方法迁移】
已知点C,D 均在线段AB 上且点C 在点D 左侧,若AC=BD,CD=a( cm),AB=b( cm)(b>a),则线段AC 的长为 cm(用含a,b 的代数式表示)。
(3)【学以致用】
已知七年级某班共有m人,在本班参加拓展课报名统计时发现,选择围棋课的人数是n(n【答案】(1)1.5
(2)
(3)解:如图,
表示七年级某班人数,
表示七年级某班男生人数,
表示七年级某班女生人数,
表示参加围棋课的男生,
表示未参加围棋课的男生,
表示未参加围棋课的女生,
表示参加围棋课的女生,
设,,则,,
∵选择围棋课的人数有人,
∴,即,解得:,
∵,
∴.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】(1)解:∵,,,
∴,
故答案为:;
()解:∵,,,
∴,
故答案为:;
【分析】()利用线段和差可得,,即可求解;
()利用线段和差,即可求解;
()根据题意画出线段图,设,,则,,根据题意,表示出m,n,即可求解;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
新人教版七年级数学上名师点拨与训练
第6章 几何图形
6.2.2线段的比较与运算
学习目标
1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.
2. 理解线段等分点的意义. 能够运用线段的和、差、倍、分关系求线段的长度.
3 .理解线段的性质,会利用线段性质解释实际问题.
4 .理解两点间的距离概念
重点:会比较两条线段的长短,会利用线段的和、差、倍、分求线段的长度
难点:简单的推理求线段的长度
老师告诉你
1.线段的和差画法注意
画线段的和、差时,均在一条射线上操作,前一条线段的终点是后一条线段的起点,若两条线段的方向相同,则表示它们的和,若两条线段的方向相反,则表示它们的差。
2.线段的中点一定在这条线段上。
知识点拨
知识点1 、线段大小比较
比较线段大小的方法:(1)目测法;(2)度量法;(3)叠合法
叠合比较法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.如下图:
注意:线段的比较方法除了叠合比较法外,度量比较法也是常用的方法.
【新知导学】
例1-1 .如图,AB=CD,那么AC与BD的大小关系是( )
A.AC=BD B.AC<BD C.AC>BD D.不能确定
例1-2. 在图中“ ”内标上字母A,B,C,使 AC
1.如图,在三角形纸片ABC 中,以下比较线段AC和AB 长短的方法,可行的有( )
①凭感觉估计.②用直尺度量出 AB 和AC 的长度.③用圆规将线段AB叠放到线段AC上,观察点 B 的位置.④沿点 A 折叠纸片,使AB和AC 重合,观察点 B 的位置.
A.①② B.①③ C.②③ D.②③④
2.如图,用圆规比较两条线段 A'B'和AB 的长短,下列结论中,正确的是( )
A. B. C. D.无法确定
.
知识点2 、线段的和与差
1.线段的和与差
如下图:线段AB上有一点C,则AC+BC=AB;AC=AB - BC; BC=AB - AC,
在这里线段AC、BC、AB表示线段的长度,如AC+BC=AB表示AC长度与BC长度之和等于AB长度。
2.尺规作图: 仅用圆规和没有刻度的直尺作图的方法叫做尺规作图
注意:
(1)只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.
(2)直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上面画刻度.
(3)圆规可以开至无限宽,但上面也不能有刻度.它只可以拉开成之前构造过的长度.
2.作一条线段等于已知线段
“作一条线段等于已知线段”的两种方法:
【方法一】尺规作图:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC上截取AB=a,则线段AB为所求;这是考试中常考点。
【方法二】度量作图:用刻度尺作一条线段等于已知线段.例如:可以先量出线段a的长度,再画一条等于这个长度的线段.
【新知导学】
例2-1. 尺规作图:已知线段 a,b,c(b>c),如图所示.
求作:一条线段,使它等于a+b-c.
解:作法:⑴如图,画射线AE;
⑵在射线AE上顺次截取AC,CD,使 AC= ,CD= ;
⑶在线段AD上截取线段DB,使DB = .
线段 为所求作的线段.
例2-2. 用直尺和圆规作一条线段,使它等于已知线段(要求保留作图痕迹)。
已知:线段a。
求作:线段AB,使AB=a。
【对应导练】
1. 如图,已知线段a,b(a>b),画一条线段x,使x=2a+b.
2.用“>”“<”或“=”填空:
(1)如果点 C 在线段 AB 上,那么 AC AB,AB BC.
(2)如果点 D 在线段AB 的延长线上,那么 AD AB,BD AD.
(3)如果点 E 在线段AB 的反向延长线上,那么 BE AE.
知识点3 、线段性质
线段的基本性质:两点的所有连线中,线段最短.简记为:两点之间,线段最短.
如图所示,在A,B两点所连的线中,线段AB的长度是最短的.
两点间的距离:连接两点间的线段的长度,叫做这两点的距离.
注意:两点的距离是指两点间线段的长度,不是两点间的线段。是一个具体的数值.
【新知导学】
例3-1.关于两点之间的线段,下列说法中不正确的是( )
A.连结两点的线段可以有无数条
B.如果线段AB=AC,那么点A与点B的距离等于点A与点C的距离
C.连结两点的线段的长度是两点间的距离
D.连结两点的线段是连结两点的所有的线中,长度最小的
例3-2.下列现象中,可用基本事实“两点之间线段最短”来解释的是( )
A.用两个钉子就可以把木条固定在墙上
B.利用圆规可以比较两条线段的大小关系
C.把弯曲的公路改直,就能缩短路程
D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
【对应导练】
1.下列说法:(1)在所有连结两点的线中,线段最短;(2)连接两点的线段叫做这两点的距离;(3)若线段 ,则点 是线段 的中点;(4)经过刨平的木板上的两个点,能弹出一条笔直的墨线,是因为两点确定一条直线,其中说法正确的是 ( )
A.(1)(2)(3) B.(1)(4)
C.(2)(3) D.(1)(2)(4)
2.下列说法中,正确的是( )
A.射线是直线的一半
B.线段AB是点A与点B的距离
C.两点之间所有连线中,线段最短
D.角的大小与角的两边所画的长短有关
3.下列说法:①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若α=29°45′,则α的补角是150°55′;⑤若AB=BC,则点B是线段AC的中点.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法:(1)两点之间的所有连线中,线段最短;(2)角是由两条具有公共端点的射线组成的;(3)经过两点有且只有一条直线;(4)连接两点的线段叫做这两点之间的距离.其中正确的有 (填正确说法的序号).
知识点4、 线段的中点
线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如图6所示,点C是线段AB的中点,则,或AB=2AC=2BC.
注意:若点C是线段AB的中点,则点C一定在线段AB上
【新知导学】
例4-1.如图,点是线段的中点,点是线段的中点,点是线段的中点,点是线段的中点.若,则 ;若,则 (用含的代数式表示).
例4-2.如图,D,E顺次为线段AB 上的两点,AB=20,C为AD 的中点,则下列选项正确的是( )
A.若BE-DE=0,则AE-CD=7 B.若BE-DE=2,则AE-CD=7
C.若BE-DE=4,则AE-CD=7 D.若BE-DE=6,则AE-CD=7
【对应导练】
1. 如图,B是线段AC上一点,且
(1)试求出线段AC的长;
(2)如果O是线段AC的中点,请求出线段OB的长.
2.如图,点C 在线段AB 上,AC=2BC,点 D在点E 的左侧。已知AB=18,DE=8,线段DE 在线段AB 上移动。
(1)当 E 为BC 的中点时,求AD 的长。
(2)若点 F(异于点A,B,C)在线段AB 上,AF=3AD,CE+EF=3,求AD 的长。
二、题型训练
1.线段的和差作图
1.用无刻度的直尺和圆规作一条线段,使它等于已知线段.
已知:线段a和线段AB(如图).
求作:延长线段AB至点C,使BC=2a(用直尺和圆规作图,不写作法,保留作图痕迹).
2. 如图,已知线段a,b,c,用圆规和直尺作一条线段,使它等于a+2b-c.
3.如图,已知平面上四个点,请按要求完成下列问题:
(1)画直线,射线,连接;
(2)在射线上作点,使得(尺规作图,保留作图浪迹);
(3)请在直线上确定一点,使最小,画出点,此画图依据是_▲_.
2.利用线段和差计算
4.(1)如图,已知线段a,b,作一条线段,使它等于a+2b.
(2)点M, N, P 在同一条直线上, MN=3cm, NP=1cm.求线段MP 的长.
5.如图,点C是线段的中点.
(1)尺规作图:在线段的延长线上作线段,使得;
(2)若(1)中的线段,求线段的长;并任选三条线段,求出它们的长度和.
6.如图,已知长度为a、b(a>b)的两条线段及射线AH.
(1)尺规作图:在射线AH上作线段AC=2a﹣b,其中AB=2a,BC=b(保留作图痕迹,不写作法);
(2)在(1)的条件下,当a=6cm、b=4cm时,若点M、N分别是线段AC、BC的中点,求线段MN的长度.
3.利用线段中点推理计算
7.如图,AB=18,C为AB 的中点,点D 在线段AC上,且AD:CB=1:3,则 DB 的长为( )
A.8 B.10 C.12 D.15
8.已知线段 ,在直线AB 上有一点C,且 D 是线段AC 的中点,求线段AD 的长.
9.如图,已知A,B,C 是数轴上的三点,O是原点,点C 表示的数为6,BC=4,AB=12。
(1)写出数轴上点 A,B表示的数。
(2)动点 P,Q分别从点A,C同时出发,点P 以每秒6个单位长度的速度沿数轴向右匀速运动,点Q 以每秒3个单位长度的速度沿数轴向左匀速运动,M为AP 的中点,点 N 在线段CQ 上,且 设运动时间为t(s)(t>0)。
①求数轴上点 M,N表示的数(用含 t 的式子表示)。
②当t 为何值时,原点O 恰为线段PQ 的中点
三、课堂达标
一、选择题(每小题4分,共32分)
1. 七年级一班的同学想举行一次拔河比赛,他们想从两条大绳子中挑出一条最长的绳子,同学们说出了几种方法,请你帮他们选择一种最合适的方法 ( )
A.把两条绳子接在一起
B.把两条绳子重合,观察另一端情况
C.把两条大绳的一端对齐,然后同一方向上拉直两条绳子,另一端在外面的即为长绳
D.以上几种方法都可以
2.下列说法中不正确的是( )
A.若点C在线段AB的延长线上,则AC>AB
B.若点C在线段AB上,则AC
D.若A,B,C三点不在一条直线上,可能AC=AB
3.已知点C在线段AB上,则下列条件中,不能确定C是线段AB中点的是( )
A.AC=BC B.AB=2BC C.AC+BC=AB D.BC=AB
4.如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
A.2cm B.4cm C.1cm D.6cm
5.如图,线段 CD 在线段AB 上,且CD=2。若线段 AB 的长度值是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段的长度之和可能是( )
A.28 B.29 C.30 D.31
6.若点A、B、C在同一条直线上,线段AB=5厘米,线段BC=2厘米,则线段AC的长为( )
A.7厘米 B.3厘米
C.7厘米或3厘米 D.不确定
7.如图,C是线段AB 的中点,D 是线段AC上的一点,且 若BC=4,则 DC 的长为 ( )
A.1 B. C. D.2
8.如图,线段,动点P从A出发,以的速度沿运动,M为的中点,N为的中点.以下说法正确的是( )
①运动后,; ②的值随着运动时间的改变而改变;③的值不变;
④当时,运动时间为.
A.①② B.②③ C.①②③ D.②③④
二、填空题(每小题4分,共20分)
9.已知线段AB的中点为点C,则线段AC与AB的数量关系为AC= AB.
10. 如图,C,D是AB 的三等分点,E 是线段CD的中点.若CE=2,则AD 的长为 .
11.如图,点C在线段AB上,已知,点D是线段AB的中点,则线段CD的长是 .
12.如图,C为线段上一点,B为的中点,,.则的长是 .
13.如图,B,C 两点把线段MN 分成三部分,且MB :BC:CN=2:3:4,P 是MN 的中点。若PC=2cm,则MN= cm。
三、解答题(每小题8分,共48分)
14.如图,已知A,B,C,D四点在同一直线上,点D在线段上.点C是线段的中点.
(1)若线段,,求线段的长度;
(2)若,且,求线段的长度.
15.如图,已知、、、四点,请按要求作图,并解答.
(1)画直线;
(2)画射线;
(3)连接与射线交于点;
(4)若点是线段的中点,,,求线段MP的长.
16.如图,已知点在线段上.
(1)尺规作图:在线段的延长线上确定一点,使得;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若点是线段的中点,且,,求的长.
17.如图,已知不在同一直线上的三点A,B,C.
(1)按下面的要求用尺规作图:连接AB,AC,作射线BC;在射线BC上取一点D,使CD=AB.
(2)用刻度尺在(1)的图中画出BC的中点M.若BC=6,AB=8,求MD的长.
18. 阅读下面材料:
在数轴上2与-1所对应的两点之间的距离为|2-(-1)|=3;
在数轴上-2与3所对应的两点之间的距离为|-2-3|=5;
在数轴上-3与-1所对应的两点之间的距离为|(-1)-(-3)|=2.
归纳:在数轴上点A,B分别表示数a,b,则A,B两点之间的距离AB=|a-b|或|b-a|.
回答下列问题:
(1)数轴上表示数x和1的两点之间的距离表示为 ;数轴上表示数x和 的两点之间的距离表示为|x+2|;
(2)试说明当表示数x的点在-2与3的对应点之间移动时,|x-3| +|x+2|的值总是一个固定的值,并求出这个固定值.
19.
(1)【问题探究】
如图,点C,D 均在线段AB 上且点C 在点 D 左侧,若AC=BD,CD=6 cm,AB=9 cm,则线段AC 的长为 cm。
(2)【方法迁移】
已知点C,D 均在线段AB 上且点C 在点D 左侧,若AC=BD,CD=a( cm),AB=b( cm)(b>a),则线段AC 的长为 cm(用含a,b 的代数式表示)。
(3)【学以致用】
已知七年级某班共有m人,在本班参加拓展课报名统计时发现,选择围棋课的人数是n(n
第6章 几何图形
6.2.2线段的比较与运算
学习目标
1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.
2. 理解线段等分点的意义. 能够运用线段的和、差、倍、分关系求线段的长度.
3 .理解线段的性质,会利用线段性质解释实际问题.
4 .理解两点间的距离概念
重点:会比较两条线段的长短,会利用线段的和、差、倍、分求线段的长度
难点:简单的推理求线段的长度
老师告诉你
1.线段的和差画法注意
画线段的和、差时,均在一条射线上操作,前一条线段的终点是后一条线段的起点,若两条线段的方向相同,则表示它们的和,若两条线段的方向相反,则表示它们的差。
2.线段的中点一定在这条线段上。
知识点拨
知识点1 、线段大小比较
比较线段大小的方法:(1)目测法;(2)度量法;(3)叠合法
叠合比较法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.如下图:
注意:线段的比较方法除了叠合比较法外,度量比较法也是常用的方法.
【新知导学】
例1-1 .如图,AB=CD,那么AC与BD的大小关系是( )
A.AC=BD B.AC<BD C.AC>BD D.不能确定
【分析】由题意已知AB=CD,根据等式的基本性质,两边都减去BC,等式仍然成立.
【解析】根据题意和图示可知AB=CD,而CB为AB和CD共有线段,故AC=BD.
故选:A.
例1-2. 在图中“ ”内标上字母A,B,C,使 AC
【解析】【分析】用观察法、叠合法或度量法比较三条线段的长短,并标记,因为AC 最短,BC最长,所以长线段、短线段的公共端点就是点C,然后确定点A,点B的位置.
【对应导练】
1.如图,在三角形纸片ABC 中,以下比较线段AC和AB 长短的方法,可行的有( )
①凭感觉估计.②用直尺度量出 AB 和AC 的长度.③用圆规将线段AB叠放到线段AC上,观察点 B 的位置.④沿点 A 折叠纸片,使AB和AC 重合,观察点 B 的位置.
A.①② B.①③ C.②③ D.②③④
【答案】D
【知识点】线段的长短比较
【解析】【解答】解:① 凭感觉估计 ,不可行,不符合题意;
②用直尺度量出 AB 和AC 的长度 ,通过测量比较,可行,符合题意;
③用圆规将线段AB叠放到线段AC上,观察点 B 的位置,根据点B在AC上还是AC外可比较,可行,符合题意 ;
④沿点 A 折叠纸片,使AB和AC 重合,观察点 B 的位置根据点B在AC上还是AC外可比较,可行,符合题意 .
故答案为:D.
【分析】根据测量法和叠合法比较线段的大小即可判断.
2.如图,用圆规比较两条线段 A'B'和AB 的长短,下列结论中,正确的是( )
A. B. C. D.无法确定
【答案】A
【知识点】线段的长短比较
【解析】【解答】解:
故答案为:A.
【分析】根据 A'B' 中,点A与A'重合,端点 B'在AB的延长线上可得 A'B' >AB.
知识点2 、线段的和与差
1.线段的和与差
如下图:线段AB上有一点C,则AC+BC=AB;AC=AB - BC; BC=AB - AC,
在这里线段AC、BC、AB表示线段的长度,如AC+BC=AB表示AC长度与BC长度之和等于AB长度。
2.尺规作图: 仅用圆规和没有刻度的直尺作图的方法叫做尺规作图
注意:
(1)只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.
(2)直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上面画刻度.
(3)圆规可以开至无限宽,但上面也不能有刻度.它只可以拉开成之前构造过的长度.
2.作一条线段等于已知线段
“作一条线段等于已知线段”的两种方法:
【方法一】尺规作图:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC上截取AB=a,则线段AB为所求;这是考试中常考点。
【方法二】度量作图:用刻度尺作一条线段等于已知线段.例如:可以先量出线段a的长度,再画一条等于这个长度的线段.
【新知导学】
例2-1. 尺规作图:已知线段 a,b,c(b>c),如图所示.
求作:一条线段,使它等于a+b-c.
解:作法:⑴如图,画射线AE;
⑵在射线AE上顺次截取AC,CD,使 AC= ,CD= ;
⑶在线段AD上截取线段DB,使DB = .
线段 为所求作的线段.
【答案】a;b;c;AB
【知识点】尺规作图-线段的和差
【解析】【解答】解:作法:⑴如图,画射线AE;
⑵在射线AE上顺次截取AC,CD,使 AC=a,CD=b,
⑶在线段AD上截取线段DB,使DB =c,
线段AB为所求作的线段.
故答案为:a,b,c,AB.
【分析】利用线段定义及作图方法作出图形即可.
例2-2. 用直尺和圆规作一条线段,使它等于已知线段(要求保留作图痕迹)。
已知:线段a。
求作:线段AB,使AB=a。
【答案】解:如图所示。
【知识点】尺规作图-线段的和差
【解析】【分析】首先画射线,然后再用圆规在射线上截取AB=a即可.
【对应导练】
1. 如图,已知线段a,b(a>b),画一条线段x,使x=2a+b.
【答案】解:如图所示:
(1)作射线OP,
(2)在射线OP上截取OA=a,AB=a,BC=b,线段OC就是所要画的线段.
【知识点】尺规作图-线段的和差
【解析】【分析】先作出射线,再在这条射线上截取2段长度等于a的线段和一段长度等于b的线段即可.
2.用“>”“<”或“=”填空:
(1)如果点 C 在线段 AB 上,那么 AC AB,AB BC.
(2)如果点 D 在线段AB 的延长线上,那么 AD AB,BD AD.
(3)如果点 E 在线段AB 的反向延长线上,那么 BE AE.
【答案】(1)<;>
(2)>;<
(3)>
【知识点】线段的长短比较
【解析】【解答】解:(1)如图.
AC
故答案为:<,>.
(2)如图.
AD>AB,BD
(3)如图.
BE>AE.
故答案为:>.
【分析】(1)画出图形,再比较AC与AB的大小,比较AB与BC的大小;
(2)画出图形,再比较AD与AB的大小,BD与AD的大小;
(3)画出图形,再比较BE与AE的大小.
知识点3 、线段性质
线段的基本性质:两点的所有连线中,线段最短.简记为:两点之间,线段最短.
如图所示,在A,B两点所连的线中,线段AB的长度是最短的.
两点间的距离:连接两点间的线段的长度,叫做这两点的距离.
注意:两点的距离是指两点间线段的长度,不是两点间的线段。是一个具体的数值.
【新知导学】
例3-1.关于两点之间的线段,下列说法中不正确的是( )
A.连结两点的线段可以有无数条
B.如果线段AB=AC,那么点A与点B的距离等于点A与点C的距离
C.连结两点的线段的长度是两点间的距离
D.连结两点的线段是连结两点的所有的线中,长度最小的
【答案】A
【知识点】线段上的两点间的距离
【解析】【解答】 A、连接两点的线段只有1条,故A错误;
B、线段AB=AC,那么点A与点B的距离等于点A与点C的距离,故B正确;
C、连接两点的线段的长度,是两点间的距离,故C正确;
D、两点之间的距离是连接两点的所有线的长度中,长度最短的,故D正确;
故答案为:A.
【分析】根据两点之间距离、线段的基本事实求解.
例3-2.下列现象中,可用基本事实“两点之间线段最短”来解释的是( )
A.用两个钉子就可以把木条固定在墙上
B.利用圆规可以比较两条线段的大小关系
C.把弯曲的公路改直,就能缩短路程
D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
【答案】C
【知识点】两点确定一条直线;两点之间线段最短;线段的长短比较
【解析】【解答】解:A、用两个钉子就可以把木条固定在墙上,是两点确定一条直线,A错误;
B、利用圆规可以比较两条线段的大小关系,是线段长度比较,B错误;
C、把弯曲的公路改直,就能缩短路程,可用基本事实“两点之间,线段最短”来解释,C正确;
D、植树时,只要定出两棵树的位置,就能确定同一行树所在的直线,是两点确定一条直线,D错误;
故答案为:C.
【分析】根据两点确定一条直线可判断A和D选项说法不符合题意;根据用圆规来比较线段的大小可判断B选项不符合题意;根据两点之间,线段最短可判断C选项说法符合题意;即可得出答案.
【对应导练】
1.下列说法:(1)在所有连结两点的线中,线段最短;(2)连接两点的线段叫做这两点的距离;(3)若线段 ,则点 是线段 的中点;(4)经过刨平的木板上的两个点,能弹出一条笔直的墨线,是因为两点确定一条直线,其中说法正确的是 ( )
A.(1)(2)(3) B.(1)(4)
C.(2)(3) D.(1)(2)(4)
【答案】B
【知识点】两点确定一条直线;两点之间线段最短;线段上的两点间的距离;线段的中点
【解析】【解答】解:(1)在所有连结两点的线中,线段最短,故原说法正确;
(2)连接两点的线段的长度叫做这两点的距离,故原说法错误;
(3)若线段AC=BC,且当点C在线段AB上时,点C才是线段AB的中点,故原说法错误;
(4)经过刨平的木板上的两个点,能弹出一条笔直的墨线,是因为两点确定一条直线,故原说法正确;
综上所述,说法正确有(1)(4).
故答案为:B.
【分析】根据两点之间线段最短的性质判断 (1);根据数轴上两点间的距离的定义判断(2);根据线段的中点的定义判断(3);根据直线的性质判断(4).
2.下列说法中,正确的是( )
A.射线是直线的一半
B.线段AB是点A与点B的距离
C.两点之间所有连线中,线段最短
D.角的大小与角的两边所画的长短有关
【答案】C
【知识点】直线、射线、线段;两点之间线段最短;线段上的两点间的距离;角的概念及表示
【解析】【解答】解:A、射线的长度无法度量,故不是直线的一半,故本选项错误;
B、线段AB的长度是点A与点B的距离,故本选项错误;
C、两点之间所有连线中,线段最短,故本选项正确;
D、角的大小与角的两边所画的长短无关,故本选项错误.
故答案为:C.
【分析】根据射线、直线、线段及角的概念、两点间的距离、线段的性质逐一分析并判断即可.
3.下列说法:①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若α=29°45′,则α的补角是150°55′;⑤若AB=BC,则点B是线段AC的中点.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【知识点】两点确定一条直线;两点之间线段最短;线段上的两点间的距离;余角、补角及其性质;线段的中点
【解析】【解答】解:①是直线的公理,故本选项正确;
②连接两点的线段的长度叫两点的距离,故本选项错误;
③是线段的性质,故本选项正确;
④若α=29°45′,则α的补角是150°15′,故本选项错误;
⑤A、B、C可能不共线,故本选项错误.
故答案为:B.
【分析】根据直线公理可判断①;距离是长度,线段是图形,故连接两点的线段的长度才叫两点的距离,据此判断②;根据线段公理判断③;和为180°的两个角互为补角,据此判断④;A、B、C可能不在同一直线上,也可能在同一条直线上,只有当三点在同一直线上的时候,点B才是线段AC的中点,据此可判断⑤.
4.下列说法:(1)两点之间的所有连线中,线段最短;(2)角是由两条具有公共端点的射线组成的;(3)经过两点有且只有一条直线;(4)连接两点的线段叫做这两点之间的距离.其中正确的有 (填正确说法的序号).
【答案】(1)(2)(3)
【知识点】两点确定一条直线;两点之间线段最短;线段上的两点间的距离;角的概念及表示
【解析】【解答】解:(1)两点之间的所有连线中,线段最短,正确;
(2)角是由两条具有公共端点的射线组成的,正确;
(3)经过两点有且只有一条直线,正确;
(4)连接两点的线段的长度叫做这两点之间的距离,故原说法错误.
故答案为:(1)(2)(3).
【分析】根据两点之间,线段最短的性质可判断(1);根据角的概念可判断(2);根据直线的概念可判断(3);根据两点间距离的概念可判断(4).
知识点4、 线段的中点
线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如图6所示,点C是线段AB的中点,则,或AB=2AC=2BC.
注意:若点C是线段AB的中点,则点C一定在线段AB上
【新知导学】
例4-1.如图,点是线段的中点,点是线段的中点,点是线段的中点,点是线段的中点.若,则 ;若,则 (用含的代数式表示).
【答案】0.5;
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵AB=8,点O是线段AB的中点,
∴OA=OB=AB=4,
∵点D是线段AO的中点,
∴AD=AO=2,BD=8 2=6,
∵点E是线段BD的中点,
∴BE=DE=3,AE=8 3=5,
∵点F是线段AE的中点,
∴AF=AE=2.5,
∴DF=AF AD=2.5 2=0.5;
设OA=OB=x,则AB=2x,BE=x a,
∵点E是线段BD的中点,
∴BD=2BE=2x 2a,
∵点D是线段AO的中点,
∴AD=AO=x,
∴AB=AD+BD=x+2x 2a=x 2a,
∴OB=AB=x a,即x a=x,
解得x=4a,
即AE=AO+OE=x+a=5a,
∵点F是线段AE的中点,
∴EF=AE=a,
∴OF=EF OE=a a=a.
故答案为:0.5;a.
【分析】根据中点的概念可得OA=OB=AB=4,AD=AO=2,则BD=AB-AD=6,同理可得BE=DE=3,AE=5,AF=AE=2.5,DF=AF-AD=0.5,设OA=OB=x,则AB=2x,BE=x-a,由中点的概念可得BD=2BE=2x-2a,AD=AO=x,则AB=AD+BD=x 2a,OB=AB=x a,结合OB=4可得x=4a,则AE=AO+OE=5a,EF=AE=a,然后根据OF=EF-OE进行计算.
例4-2.如图,D,E顺次为线段AB 上的两点,AB=20,C为AD 的中点,则下列选项正确的是( )
A.若BE-DE=0,则AE-CD=7 B.若BE-DE=2,则AE-CD=7
C.若BE-DE=4,则AE-CD=7 D.若BE-DE=6,则AE-CD=7
【答案】D
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:由 BE-DE=0,可设DE=x,则BE=x,
∴AD=20-x-x=20-2x,
∵C为AD 的中点,
∴AC=CD=10-x,AE=20-2x+x=20-x,
∴AE-CD=(20-x)-(10-x)=10,故A错误;
由 BE-DE=2,可设DE=x,则 BE=x+2,
∴AD=20-x-(x+2)=18-2x,
∵C为AD 的中点,
∴AC=CD=9-x,AE=18-2x+x=18-x,
∴AE-CD=(18-x)-(9-x)=9,故B错误;
由BE-DE=4,可设DE=x,则 BE=x+4,
∴AD=20-x-(x+4)=16-2x,
∵C为AD的中点,
∴AC=CD=8-x,AE=16-2x+x=16-x,
∴AE-CD=(16-x)-(8-x)=8,故C错误;
由BE-DE=6,可设DE=x,则BE=x+6,
∴AD=20-x-(x+6)=14-2x,
∵C为AD的中点,
∴AC=CD=7-x,AE=14-2x+x=14-x,
∴AE-CD=(14-x)-(7-x)=7,故D正确。
故答案为:D.
【分析】根据线段中点的定义与线段的和差逐项分析可得答案.
【对应导练】
1. 如图,B是线段AC上一点,且
(1)试求出线段AC的长;
(2)如果O是线段AC的中点,请求出线段OB的长.
【答案】(1)解:∵AB=21cm,BC=AB,
∴BC=×21=7(cm),
∴AC=AB+BC=21+7=28(cm).
(2)解:∵O是线段AC的中点,
∴OC=AC=14cm,
∴OB=OC BC=14 7=7(cm).
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】(1)根据“BC=AB”求出BC的长,再利用线段的和差求出AC的长即可;
(2)先利用线段中点的性质求出OC的长,再利用线段的和差求出OB的长即可.
2.如图,点C 在线段AB 上,AC=2BC,点 D在点E 的左侧。已知AB=18,DE=8,线段DE 在线段AB 上移动。
(1)当 E 为BC 的中点时,求AD 的长。
(2)若点 F(异于点A,B,C)在线段AB 上,AF=3AD,CE+EF=3,求AD 的长。
【答案】(1)解:∵,,,
∴,,
如图,
∵E为BC中点,
∴,
∴,
∴;
(2)解:由题意,得AF=3AD,AE=AD+DE=AD+8,
分类讨论:
①如图,当点E在点F的左侧时,
∵,,
∴,,
∵,,
∴点F是BC的中点,
∴,
∴,
∴;
②如图,当点E在点F的右侧,
∵,,
∴,
∴,
∴.
综上所述:AD的长为3或5;
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】(1)由,,可求出,.再根据E为BC中点,即得出,从而可求出CD的长,进而可求出AD的长;
(2)分类讨论:当点E在点F的左侧时和当点E在点F的右侧时,画出图形,根据线段的倍数关系和和差关系,利用数形结合的思想即可解题.
二、题型训练
1.线段的和差作图
1.用无刻度的直尺和圆规作一条线段,使它等于已知线段.
已知:线段a和线段AB(如图).
求作:延长线段AB至点C,使BC=2a(用直尺和圆规作图,不写作法,保留作图痕迹).
【答案】解:如图:
【知识点】尺规作图-线段的和差
【解析】【分析】根据尺规作图步骤:延长AB,以点B为圆心,a为半径做弧,交延长线于点D,再以点D为圆心,a为半径做弧,交延长线于点C,即为所求.
2. 如图,已知线段a,b,c,用圆规和直尺作一条线段,使它等于a+2b-c.
【答案】解:如图:AE=a+2b-c即为所求:
作图步骤如下:
①作射线AM;
②在射线AM上依次截取AB=a,BC=CD=b;
③在线段AD上截取DE=c;
④则线段AE=AB+BC+CD-DE=a+2b-c;
线段AE即可为所求.
【知识点】尺规作图-线段的和差
【解析】【分析】①作射线AM;②在射线AM上依次截取AB=a,BC=CD=b;③在线段AD上截取DE=c;④则线段AE=AB+BC+CD-DE=a+2b-c;线段AE即可为所求.
3.如图,已知平面上四个点,请按要求完成下列问题:
(1)画直线,射线,连接;
(2)在射线上作点,使得(尺规作图,保留作图浪迹);
(3)请在直线上确定一点,使最小,画出点,此画图依据是_▲_.
【答案】(1)如下图所示:
直线,射线,线段为求作的;
(2)以A为圆心,的长为半径画弧,交射线于点P,如下图所示,
线段为求作图形;
(3)连接,交于点Q,如下图所示:
点Q为求作的点,
依据:两点之间,线段最短.
【知识点】两点之间线段最短;尺规作图-直线、射线、线段;尺规作图-线段的和差
【解析】【分析】(1)根据直线,射线,线段的定义画出图形即可;
(2)以A为圆心,DC为半径作弧,交AB于点P,点P即为所求;
(3)连接PD交AC于点Q,点Q即为所求.
2.利用线段和差计算
4.(1)如图,已知线段a,b,作一条线段,使它等于a+2b.
(2)点M, N, P 在同一条直线上, MN=3cm, NP=1cm.求线段MP 的长.
【答案】解:(1)作射线AM;
在射线AM上依次截取AB=a,BC=CD=b,
则线段AD=a+2b即为所求;
(2)当点P在线段MN上,如图(1)
∵ MN=3cm, NP=1cm ,
∴MN=MN-MP=3-1=2cm.
当点P在线段MN的延长线上,如图(2)
∵ MN=3cm, NP=1cm ,
∴MN=MN+MP=3+1=4cm.
故线段MP的长为2cm或4cm.
【知识点】尺规作图-线段的和差
【解析】【分析】(1)作射线AM;在射线AM上依次截取AB=a,BC=CD=b;则线段AD=a+2b即为所求;
(2)分点P在线段MN上和点P在线段MN的延长线上两种情况作线段的和差运算即可.
5.如图,点C是线段的中点.
(1)尺规作图:在线段的延长线上作线段,使得;
(2)若(1)中的线段,求线段的长;并任选三条线段,求出它们的长度和.
【答案】(1)解:如图,延长线段,以B为圆心为半径画圆弧交延长线于一点即为D点,
(2)解:由(1)得B为的中点,
∵,
∴
∵C为的中点,
∴
∴(答案不唯一).
【知识点】线段的中点;线段的和、差、倍、分的简单计算;尺规作图-线段的和差
【解析】【分析】(1)延长线段,以B为圆心为半径画圆弧交延长线于一点即为D点;
(2)利用线段中点的性质及线段的和差分析求解即可.
6.如图,已知长度为a、b(a>b)的两条线段及射线AH.
(1)尺规作图:在射线AH上作线段AC=2a﹣b,其中AB=2a,BC=b(保留作图痕迹,不写作法);
(2)在(1)的条件下,当a=6cm、b=4cm时,若点M、N分别是线段AC、BC的中点,求线段MN的长度.
【答案】(1)解:如图所示,
(2)解:当、时,,
、分别是线段、的中点
,.
.
【知识点】线段的中点;线段的和、差、倍、分的简单计算;尺规作图-线段的和差
【解析】【分析】(1)以点为圆心,线段的长为半径画弧,交射线于点,再以点为圆心,线段的长为半径画弧,交射线于点,再以点为圆心,线段的长为半径画弧,交线段于点,则线段即为所作图.
(2)由题意可得,,根据中点的定义可求出,,再利用线段运算可得:,代入数据可求出答案.
3.利用线段中点推理计算
7.如图,AB=18,C为AB 的中点,点D 在线段AC上,且AD:CB=1:3,则 DB 的长为( )
A.8 B.10 C.12 D.15
【答案】D
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵,点C为的中点,
∴,
∵,
∴,
∴.
故答案为:D
【分析】根据线段中点的定义可得,再求出,然后根据,代入数据计算即可得解.
8.已知线段 ,在直线AB 上有一点C,且 D 是线段AC 的中点,求线段AD 的长.
【答案】解:分两种情况讨论:
①如图1所示,当点C在点A与B之间时,
∵线段,,
∴,
∵D是线段的中点,
∴;
②当点C在点B的右侧时,如图2所示:
∵线段,,
∴,
∵D是线段的中点,
∴;
综上所述,线段的长为或.
【知识点】线段的中点;线段的和、差、倍、分的简单计算;分类讨论
【解析】【分析】应考虑到A、B、C三点之间的位置关系的多种可能,即点C在点A与B之间或点C在点B的右侧两种情况进行分类讨论.
9.如图,已知A,B,C 是数轴上的三点,O是原点,点C 表示的数为6,BC=4,AB=12。
(1)写出数轴上点 A,B表示的数。
(2)动点 P,Q分别从点A,C同时出发,点P 以每秒6个单位长度的速度沿数轴向右匀速运动,点Q 以每秒3个单位长度的速度沿数轴向左匀速运动,M为AP 的中点,点 N 在线段CQ 上,且 设运动时间为t(s)(t>0)。
①求数轴上点 M,N表示的数(用含 t 的式子表示)。
②当t 为何值时,原点O 恰为线段PQ 的中点
【答案】(1)解:∵点C 表示的数为6,BC=4,
∴OB=6-4=2,
∴点 B 表示的数为2。
∵AB=12,
∴AO=12-2=10,
∴点A 表示的数为-10
(2)解:①由题意可知:AP=6t,CQ=3t。
∵M 为AP 的中点,
∴在数轴上点 M 表示的数是-10+3t。
∵点 N 在CQ上,
∴在数轴上点 N 表示的数是6-t。
②分两种情况讨论:
i.如解图①,当点 P 在点O 的左侧,点Q 在点O的右侧时,。
∵O为PQ 的中点,∴OP=OQ,
∴10-6t=6-3t,解得
ii.如解图②,当点 P 在点O 的右侧,点 Q 在点O 的左侧时,。
∵O为PQ 的中点,∴,
∴,解得 (此时AP=8<10,不合题意,舍去)。
综上所述,当 时,原点O恰为线段PQ 的中点
【知识点】一元一次方程的其他应用;线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】(1)根据数轴上两点间的距离即可求出A、B表示的数;
(2)①根据距离=速度×时间可得AP=6t,CQ=3t,根据中点性质可得AM=3t,根据 可得CN=t,根据线段的和差关系即可得答案;②根据中点定义可得,分两种情况,当点 P 在点O 的左侧,点Q 在点O的右侧时或者当点 P 在点O 的右侧,点 Q 在点O 的左侧时,再根据数轴的性质解答即可.
三、课堂达标
一、选择题(每小题4分,共32分)
1. 七年级一班的同学想举行一次拔河比赛,他们想从两条大绳子中挑出一条最长的绳子,同学们说出了几种方法,请你帮他们选择一种最合适的方法 ( )
A.把两条绳子接在一起
B.把两条绳子重合,观察另一端情况
C.把两条大绳的一端对齐,然后同一方向上拉直两条绳子,另一端在外面的即为长绳
D.以上几种方法都可以
【答案】C
【知识点】线段的长短比较
【解析】【解答】解:利用叠合法,即把两条大绳的一端对齐,然后同一方向上拉直两条绳子,另一端在外面的即为长绳.
故答案为:C.
【分析】利用叠合法判断,判断哪个选项中叠合的步骤正确即可.
2.下列说法中不正确的是( )
A.若点C在线段AB的延长线上,则AC>AB
B.若点C在线段AB上,则AC
D.若A,B,C三点不在一条直线上,可能AC=AB
【答案】C
【知识点】线段的长短比较
【解析】【解答】A.如图, 点C在线段AB的延长线上, AC=AB+BC>AB,即AC>AB,故正确;
B.如图, 若点C在线段AB上, AC=AB-BC
故答案为:C.
【分析】分别根据各选项画出图形,再写出式子比较大小,然后判断正确与否,再选出错误的.
3.已知点C在线段AB上,则下列条件中,不能确定C是线段AB中点的是( )
A.AC=BC B.AB=2BC C.AC+BC=AB D.BC=AB
【答案】C
【知识点】线段的中点
【解析】【解答】解:若点C为线段AB中点,
∴
而无论点C在线段AB的任意一位置,
都有:
故答案为:C.
【分析】根据中点的性质,逐项判断即可.
4.如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
A.2cm B.4cm C.1cm D.6cm
【答案】B
【知识点】线段上的两点间的距离
【解析】【解答】解:∵点M是AC的中点,点N是BC的中点,
∴AC=2MC,BC=2NC,
∴AC﹣BC=(MC﹣NC)×2=2×2=4(cm),
即AC比BC长4cm.
故选:B.
【分析】根据点M是AC的中点,点N是BC的中点,可得AC=2MC,BC=2NC,所以AC﹣BC=(MC﹣NC)×2,据此解答即可.
5.如图,线段 CD 在线段AB 上,且CD=2。若线段 AB 的长度值是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段的长度之和可能是( )
A.28 B.29 C.30 D.31
【答案】B
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】以这四点中任意两点为端点的所有线段为:
设,则b为正整数
由图可知,
又
则能够整除3
观察四个选项可知,只有B选项符合要求
故答案为:B.
【分析】先写出以这四点中任意两点为端点的所有线段,从而可得出所求的所有线段之和,再根据线段的和差、整数性判断即可.
6.若点A、B、C在同一条直线上,线段AB=5厘米,线段BC=2厘米,则线段AC的长为( )
A.7厘米 B.3厘米
C.7厘米或3厘米 D.不确定
【答案】C
【知识点】线段的和、差、倍、分的简单计算
【解析】【解答】解:解:当C在线段AB上时:AC=AB-BC=5-2=3(厘米);
当C在AB的延长线上时:AC=AB+BC=5+2=7(厘米);
综上,线段AC的长为7厘米或3厘米.
故答案为:C.
【分析】分两种情况讨论:即C在线段AB上,C在AB的延长线上,分别列式计算即可.
7.如图,C是线段AB 的中点,D 是线段AC上的一点,且 若BC=4,则 DC 的长为 ( )
A.1 B. C. D.2
【答案】A
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵C是AB的中点,BC=4,
∴AC=BC=4,
∵DC=AC,
∴DC=1;
故答案为:A.
【分析】根据线段的中点,可得出AC的长度,再根据DC=AC,即可得出DC的长度.
8.如图,线段,动点P从A出发,以的速度沿运动,M为的中点,N为的中点.以下说法正确的是( )
①运动后,; ②的值随着运动时间的改变而改变;③的值不变;
④当时,运动时间为.
A.①② B.②③ C.①②③ D.②③④
【答案】D
【知识点】线段的中点;一元一次方程的实际应用-行程问题;线段的和、差、倍、分的简单计算
【解析】【解答】解:①运动4s后,AP=2×4=8cm,PB=AB-AP=16cm,
∵M为的中点 ,
∴AM=MP=4cm,
∴PB=4AM,故①错误;
设运动ts时,AP=2t,PB=24-2t,
∵M为的中点,N为的中点,
∴AM=PM=t,PN=BN=12-t,
∴PM+MN=PM+PM+PN=t+t+12-t=12+t,
∴的值随着运动时间的改变而改变 ,故②正确;
∵MB=AB-AM=24-t,PB=AB-AP=24-2t,
∴=2(24-t)-(24-2t)=24cm,故③正确;
由AN=AP+PN=2t+(12-t)=12+t,PM=t,
∵ ,
∴12+t=6t,解得t=2.4s,故④正确.
故答案为:D.
【分析】根据题意分别求出AP、PB的长,再利用线段的中点得出AM、PM、PN、BN的长,利用线段的和差关系逐一求解即可判断.
二、填空题(每小题4分,共20分)
9.已知线段AB的中点为点C,则线段AC与AB的数量关系为AC= AB.
【答案】
【知识点】线段的中点
【解析】【解答】解: ∵线段AB的中点为点C ,
∴AC=BC=AB.
故答案为:.
【分析】根据线段的中点定义进行解答即可.
10. 如图,C,D是AB 的三等分点,E 是线段CD的中点.若CE=2,则AD 的长为 .
【答案】8
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:如∵ C,D是AB 的三等分点
∴AC=CD=AB
∵E 是线段CD的中点.
∴AE=AB
又∵AE-AC=EC
∴AB-AB=2
∴AB=12
∴AC=CD=AB=×12=4
∴AD=AC+CD
=4+4
=8
∴故答案为:8.
【分析】由线段三等分点、中点的定义可知:C=CD=AB,AE=AB,再线段的差关系得到:AB-AB=2,从而求出AB,再用线段的倍数关系可求出:AC=CD=AB,再由线段的和关系:AD=AC+CD即可求解.
11.如图,点C在线段AB上,已知,点D是线段AB的中点,则线段CD的长是 .
【答案】1
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵AB=10,D是线段AB的中点,
∴BD=AB=4,
∵CB=3,
∴CD=DB BC=1,
故答案为:1.
【分析】先利用线段中点的性质求出BD=AB=4,再利用线段的和差求出CD的长即可.
12.如图,C为线段上一点,B为的中点,,.则的长是 .
【答案】
【知识点】线段的中点
【解析】【解答】解:∵B为的中点,
∴,
∴,
故答案为:
【分析】本题考查了与线段中点有关的计算,由B为的中点,得到,结合,进行计算,即可求解.
13.如图,B,C 两点把线段MN 分成三部分,且MB :BC:CN=2:3:4,P 是MN 的中点。若PC=2cm,则MN= cm。
【答案】36
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵,
∴设,
则,
∵点P是的中点,
∴,
∴,
∵,
∴,
解得,
∴.
故答案为:.
【分析】根据线段比例,设设,则,列出一元一次方程求解即可.本题考查两点间的距离,弄清楚线段之间的数量关系是关键.
三、解答题(每小题8分,共48分)
14.如图,已知A,B,C,D四点在同一直线上,点D在线段上.点C是线段的中点.
(1)若线段,,求线段的长度;
(2)若,且,求线段的长度.
【答案】(1)解:∵,点C是线段的中点,
∴,
∵,
∴
(2)解:∵点C是线段的中点,
∴设,
∵,
∴,,
∵,
∴,
解得,
∴
【知识点】线段的中点;一元一次方程的实际应用-几何问题;线段的和、差、倍、分的简单计算
【解析】【分析】(1)先由“ 点C是线段的中点 ”,求出BC的长,在根据“”,可知CD为BC的,即可求出CD长;
(2)通过设未知数x,分别表示出AD和BD的长,在根据条件“ ”,即可列出等式,继而可求出x的值,得到AB的长.
15.如图,已知、、、四点,请按要求作图,并解答.
(1)画直线;
(2)画射线;
(3)连接与射线交于点;
(4)若点是线段的中点,,,求线段MP的长.
【答案】(1)图见解析,直线即为所求;
(2)图见解析,射线即为所求;
(3)图见解析,线段、点即为所求;
(4)∵,
∴DB = DP+BP = 10
∵M是BD中点
∴BM =DB = 5
∴MP = BM-BP = 5-3 = 2
【知识点】线段的中点;尺规作图-直线、射线、线段;线段的和、差、倍、分的简单计算
【解析】【解答】解:(1)如图,直线即为所求;
(2)如图,射线即为所求;
(3)如图,点P即为所求;
【分析】(1)根据直线的定义画图即可;
(2)根据射线的定义画图即可;
(3)根据线段的定义画图即可;
(4)由DB = DP+BP 求出DB的长,再由线段的中的的定义求出BM的长,利用MP = BM-BP即可求解.
16.如图,已知点在线段上.
(1)尺规作图:在线段的延长线上确定一点,使得;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若点是线段的中点,且,,求的长.
【答案】(1)解:∵,
∴点即为所求,
(2)解:∵点是线段的中点,,,
∴,
∴,
∵,
∴,
∴.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】(1)根据题意,以D为圆心,AB长为半径作弧交的延长线于点 ,点即为所求;
(2)根据中点的定义可知, 由,, 计算求解即可得到答案.
17.如图,已知不在同一直线上的三点A,B,C.
(1)按下面的要求用尺规作图:连接AB,AC,作射线BC;在射线BC上取一点D,使CD=AB.
(2)用刻度尺在(1)的图中画出BC的中点M.若BC=6,AB=8,求MD的长.
【答案】(1)解:如图,点D即为所求;
;
(2)解:∵M是BC的中点.∴CM=BC=3,
∵CD=AB=8,
∴MD=CM+CD=3+8=11.
【知识点】线段的中点;尺规作图-直线、射线、线段;线段的和、差、倍、分的简单计算
【解析】【分析】(1)根据线段、射线定义,两点确定一条直线,且由线段的一端无限延长所形成的直的线,有且仅有一个端点,无法测量长度,即可完成作图;
(2)根据线段中点定义,结合CM=BC,求得CM=3,再由MD=CM+CD,进而可得MD的长.
18. 阅读下面材料:
在数轴上2与-1所对应的两点之间的距离为|2-(-1)|=3;
在数轴上-2与3所对应的两点之间的距离为|-2-3|=5;
在数轴上-3与-1所对应的两点之间的距离为|(-1)-(-3)|=2.
归纳:在数轴上点A,B分别表示数a,b,则A,B两点之间的距离AB=|a-b|或|b-a|.
回答下列问题:
(1)数轴上表示数x和1的两点之间的距离表示为 ;数轴上表示数x和 的两点之间的距离表示为|x+2|;
(2)试说明当表示数x的点在-2与3的对应点之间移动时,|x-3| +|x+2|的值总是一个固定的值,并求出这个固定值.
【答案】(1);-2
(2)解:因为-2
=3-x+x+2
=5.
即当表示数x的点在-2与3的对应点之间移动时,|x-3|+|x+2|的值总是一个固定的值,这个固定值为5.
【知识点】数轴及有理数在数轴上的表示;绝对值及有理数的绝对值;线段上的两点间的距离
【解析】【解答】解:(1) 数轴上表示数x和1的两点之间的距离表示为 ;数轴上表示数x和-2的两点之间的距离表示为|x+2|;
故答案为: ,|x+2|,
【分析】(1)根据两点间的距离公式解答即可;
(2)由题意得-2
(1)【问题探究】
如图,点C,D 均在线段AB 上且点C 在点 D 左侧,若AC=BD,CD=6 cm,AB=9 cm,则线段AC 的长为 cm。
(2)【方法迁移】
已知点C,D 均在线段AB 上且点C 在点D 左侧,若AC=BD,CD=a( cm),AB=b( cm)(b>a),则线段AC 的长为 cm(用含a,b 的代数式表示)。
(3)【学以致用】
已知七年级某班共有m人,在本班参加拓展课报名统计时发现,选择围棋课的人数是n(n
(2)
(3)解:如图,
表示七年级某班人数,
表示七年级某班男生人数,
表示七年级某班女生人数,
表示参加围棋课的男生,
表示未参加围棋课的男生,
表示未参加围棋课的女生,
表示参加围棋课的女生,
设,,则,,
∵选择围棋课的人数有人,
∴,即,解得:,
∵,
∴.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】(1)解:∵,,,
∴,
故答案为:;
()解:∵,,,
∴,
故答案为:;
【分析】()利用线段和差可得,,即可求解;
()利用线段和差,即可求解;
()根据题意画出线段图,设,,则,,根据题意,表示出m,n,即可求解;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
