人教A版2019必修第一册2.2.3 一元二次不等式及其解法 课件(共18张PPT)
文档属性
| 名称 | 人教A版2019必修第一册2.2.3 一元二次不等式及其解法 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 12:32:26 | ||
图片预览






文档简介
(共18张PPT)
2.2.3一元二次不等式的解法(1)
1.通过实例了解一元二次不等式.
2.理解一元二次方程、一元二次不等式与相应二次函数的关系.(难点)
3.掌握简单一元二次不等式的解法.(重点)
复习导入:(一题多解)解一元二次方程
汽车在行驶中,由于惯性,刹车后还要继续向前滑行一段距离才能停止,一般称这段距离为“刹车距离”刹车距离是分析交通事故的一个重要依据.
在一个限速为40km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事后现场勘查,测得甲车的刹车距离略超过6m,乙车的刹车距离略超过10m。已知甲、乙两种车型的刹车距离m与车速km/h之问的关系分别为
,
试判断甲、乙两车有无超速现象.
探究点1 一元二次不等式的定义
思考1:在上述情境中,要判断甲、乙两车是否超速,就是要得到它们车速的取值范围,你能列出不等式解决这个问题吗?
【解析】甲: ,乙:
即和
思考2:这两个不等式有什么共同点?
【解析】有两个共同点
(1)含有一个未知数;(2)未知数的最高次数为2.
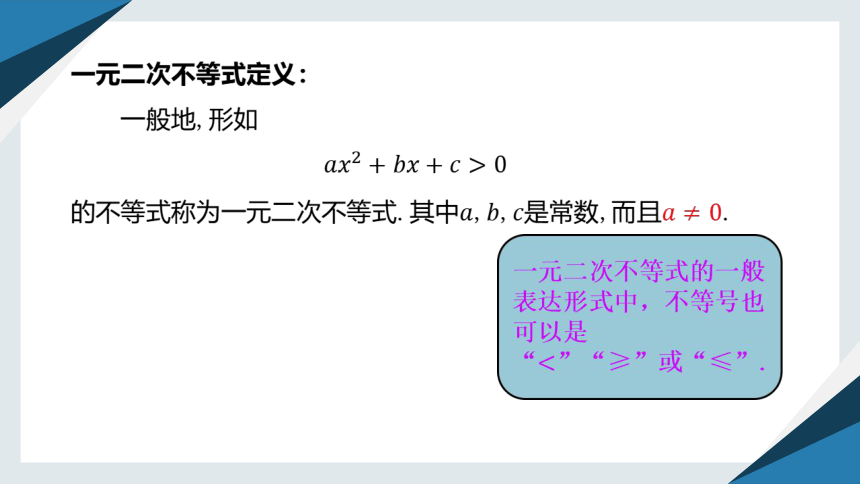
一元二次不等式定义:
一般地,形如
的不等式称为一元二次不等式.其中,,是常数,而且.
一元二次不等式的一般表达形式中,不等号也可以是
“”“≥”或“≤”.
下列不等式中,哪些是一元二次不等式
(其中a,b,c,m为常数)
(1)ax2>0; (2)x3+5x-6≥0; (3)-x-x2≤0;
(4)x2>0; (5)mx2-5y>0; (6)ax2+bx+c≤0
思考:如何解一元二次不等式呢?
探究点2 一元二次不等式的解法
思考3:对于一元二次不等式,
(1)集合中哪些数是不等式的解?
(2)不等式的解还有吗?如何解这个不等式?
【解析】(1)是不等式的解;
同号
或
(2)不等式可化为两个不等式组
或
解得或,
因此,不等式的解集为.
思考4:一元二次不等式如何解?
【解析】不等式可化为两个不等式组
或
解得,
因此,不等式的解集为.
异号
或
追问:根据上述问题你能说出一元二次不等式(或)的解集吗?
一般地,如果,则不等式的解集是
不等式的解集是
【总结】
练一练:1.不等式的解集是 .
2.不等式的解集是 .
3.不等式的解集是 .
口诀:小于号取中间,大于号取两边
思考:如果换成“≥”或“≤”呢?
例1.求不等式的解集.
【解析】因为.
所以不等式等价于,
因此,所求解集为.
一元二次不等式的一般形式可通过因式分解进行等价转化.
跟踪训练:求问题情景中不等式的解集.
【解析】可化为
,
解得(舍去)或
因此甲车的车速略大于30km/h.
【解析】可化为
,
解得(舍去)或
因此乙车的车速略大于50km/h.
小试牛刀:解不等式
不等式的解集为(-1,2)
注意:先保证二次项系数为正
上述一元二次不等式的解法,使用的主要工具是因式分解.这种方法只能在不等式是特殊类型时才比较方便,那么一般情况该怎么办呢?
思考:下列不等式的解集是什么?
(1);(2);(3).
【解析】因为任何一个实数的平方一定是一个非负数,
因此,(1)解集为;(2)解集为;
(3)两边同时开根号可得,
即,解得,因此,解集为.
变式训练:下列不等式的解集是什么?
(1);(2);
(3).
小试牛刀:求不等式
的解集
可以配方为
小结:
若因式分解不行,则配方
例2.求下列不等式的解集:
(1); (2);
(3);(4).
【解析】
(1)因为.
所以原不等式可化为,即,
两边开平方得,从而或,
解得或,
所以原不等式的解集为.
(2)因为.
所以原不等式可化为,即,
两边开平方得,从而,
解得,
所以原不等式的解集为.
(3)原不等式可化为
又因为.
所以原不等式可化为,解得,
所以原不等式的解集为.
(4)原不等式可化为
因为.
所以原不等式可化为,
即,
所以原不等式的解集为.
配方法:一元二次不等式通过配方可以转化为或的形式.当时,直接得到解集;当时,两边开根号转化为绝对值不等式.
当堂检测.求下列不等式的解集:
(1); (2).
【解析】
(1).
所以原不等式可化为
,即,
两边开平方得,
从而
解得
所以原不等式的解集为
.
(2)原不等式可化为
因为.
所以原不等式可化为
,
即,所以
所以或
解得或
所以原不等式的解集为
.
方法 不等式类型 解法
因式分解法
配方法
>0
(或)
解集为
或
(或)
时,
转化为
或
2.2.3一元二次不等式的解法(1)
1.通过实例了解一元二次不等式.
2.理解一元二次方程、一元二次不等式与相应二次函数的关系.(难点)
3.掌握简单一元二次不等式的解法.(重点)
复习导入:(一题多解)解一元二次方程
汽车在行驶中,由于惯性,刹车后还要继续向前滑行一段距离才能停止,一般称这段距离为“刹车距离”刹车距离是分析交通事故的一个重要依据.
在一个限速为40km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事后现场勘查,测得甲车的刹车距离略超过6m,乙车的刹车距离略超过10m。已知甲、乙两种车型的刹车距离m与车速km/h之问的关系分别为
,
试判断甲、乙两车有无超速现象.
探究点1 一元二次不等式的定义
思考1:在上述情境中,要判断甲、乙两车是否超速,就是要得到它们车速的取值范围,你能列出不等式解决这个问题吗?
【解析】甲: ,乙:
即和
思考2:这两个不等式有什么共同点?
【解析】有两个共同点
(1)含有一个未知数;(2)未知数的最高次数为2.
一元二次不等式定义:
一般地,形如
的不等式称为一元二次不等式.其中,,是常数,而且.
一元二次不等式的一般表达形式中,不等号也可以是
“”“≥”或“≤”.
下列不等式中,哪些是一元二次不等式
(其中a,b,c,m为常数)
(1)ax2>0; (2)x3+5x-6≥0; (3)-x-x2≤0;
(4)x2>0; (5)mx2-5y>0; (6)ax2+bx+c≤0
思考:如何解一元二次不等式呢?
探究点2 一元二次不等式的解法
思考3:对于一元二次不等式,
(1)集合中哪些数是不等式的解?
(2)不等式的解还有吗?如何解这个不等式?
【解析】(1)是不等式的解;
同号
或
(2)不等式可化为两个不等式组
或
解得或,
因此,不等式的解集为.
思考4:一元二次不等式如何解?
【解析】不等式可化为两个不等式组
或
解得,
因此,不等式的解集为.
异号
或
追问:根据上述问题你能说出一元二次不等式(或)的解集吗?
一般地,如果,则不等式的解集是
不等式的解集是
【总结】
练一练:1.不等式的解集是 .
2.不等式的解集是 .
3.不等式的解集是 .
口诀:小于号取中间,大于号取两边
思考:如果换成“≥”或“≤”呢?
例1.求不等式的解集.
【解析】因为.
所以不等式等价于,
因此,所求解集为.
一元二次不等式的一般形式可通过因式分解进行等价转化.
跟踪训练:求问题情景中不等式的解集.
【解析】可化为
,
解得(舍去)或
因此甲车的车速略大于30km/h.
【解析】可化为
,
解得(舍去)或
因此乙车的车速略大于50km/h.
小试牛刀:解不等式
不等式的解集为(-1,2)
注意:先保证二次项系数为正
上述一元二次不等式的解法,使用的主要工具是因式分解.这种方法只能在不等式是特殊类型时才比较方便,那么一般情况该怎么办呢?
思考:下列不等式的解集是什么?
(1);(2);(3).
【解析】因为任何一个实数的平方一定是一个非负数,
因此,(1)解集为;(2)解集为;
(3)两边同时开根号可得,
即,解得,因此,解集为.
变式训练:下列不等式的解集是什么?
(1);(2);
(3).
小试牛刀:求不等式
的解集
可以配方为
小结:
若因式分解不行,则配方
例2.求下列不等式的解集:
(1); (2);
(3);(4).
【解析】
(1)因为.
所以原不等式可化为,即,
两边开平方得,从而或,
解得或,
所以原不等式的解集为.
(2)因为.
所以原不等式可化为,即,
两边开平方得,从而,
解得,
所以原不等式的解集为.
(3)原不等式可化为
又因为.
所以原不等式可化为,解得,
所以原不等式的解集为.
(4)原不等式可化为
因为.
所以原不等式可化为,
即,
所以原不等式的解集为.
配方法:一元二次不等式通过配方可以转化为或的形式.当时,直接得到解集;当时,两边开根号转化为绝对值不等式.
当堂检测.求下列不等式的解集:
(1); (2).
【解析】
(1).
所以原不等式可化为
,即,
两边开平方得,
从而
解得
所以原不等式的解集为
.
(2)原不等式可化为
因为.
所以原不等式可化为
,
即,所以
所以或
解得或
所以原不等式的解集为
.
方法 不等式类型 解法
因式分解法
配方法
>0
(或)
解集为
或
(或)
时,
转化为
或
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
