新人教版七年级数学上名师点拨与训练第6章几何图形6.3.1 角
文档属性
| 名称 | 新人教版七年级数学上名师点拨与训练第6章几何图形6.3.1 角 |

|
|
| 格式 | doc | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-29 11:38:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
新人教版七年级数学上名师点拨与训练
第6章 几何图形
6.3.1 角
学习目标:
1.理解角的两种定义和相关概念,掌握角的表示方法.
2.会正确使用量角器测量角的大小.
3.认识角的单位,会进行度、分、秒之间的换算.
重点:角的两种定义以及三种表示方法.
难点:度、分、秒及其换算.
老师告诉你
角的表示方法
知识点拨
知识点1、角的概念
角的定义:
(1)定义一:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边.如图1所示,角的顶点是点O,边是射线OA、OB.
(2)定义二:一条射线绕着它的端点旋转而形成的图形,射线旋转时经过的平面部分是角的内部.如图2所示,射线OA绕它的端点O旋转到OB的位置时,形成的图形叫做角,起始位置OA是角的始边,终止位置OB是角的终边.
2.注意:
(1)两条射线有公共端点,即角的顶点;角的边是射线;角的大小与角的两边的长短无关.
(2)平角与周角:如图1所示射线OA绕点O旋转,当终止位置OB和起始位置OA成一条直线时,所形成的角叫做平角,如图2所示继续旋转,OB和OA重合时,所形成的角叫做周角.
【新知导学】
例1-1.图中以OC为边的角有几个?请把它们表示出来.
【对应导练】
1.下列关于角的说法正确的个数是( )
①角是由两条射线组成的图形;②角的边越长,角越大;③在角一边延长线上取一点D;④角可以看作由一条射线绕着它的端点旋转而形成的图形.
A.1 B.2 C.3 D.4
2.下列关于平角、周角的说法正确的是( )
A.平角是一条直线 B.周角是一条射线
C.反向延长射线OA,就形成一个平角 D.两个锐角的和不一定小于平角
知识点2 、角的表示
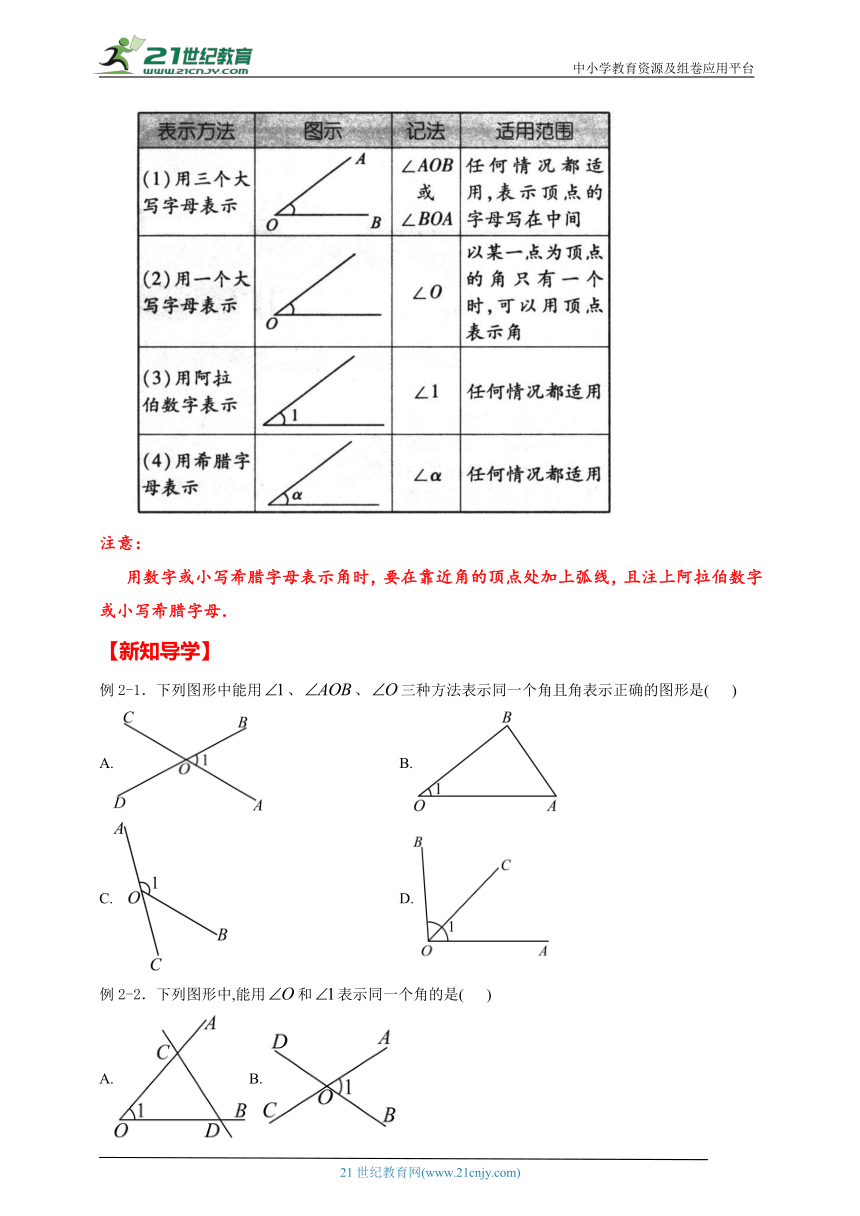
角的几何符号用“∠”表示,角的表示法通常有以下四种:
注意:
用数字或小写希腊字母表示角时,要在靠近角的顶点处加上弧线,且注上阿拉伯数字或小写希腊字母.
【新知导学】
例2-1.下列图形中能用、、三种方法表示同一个角且角表示正确的图形是( )
A. B.
C. D.
例2-2.下列图形中,能用和表示同一个角的是( )
A. B.
C. D.
【对应导练】
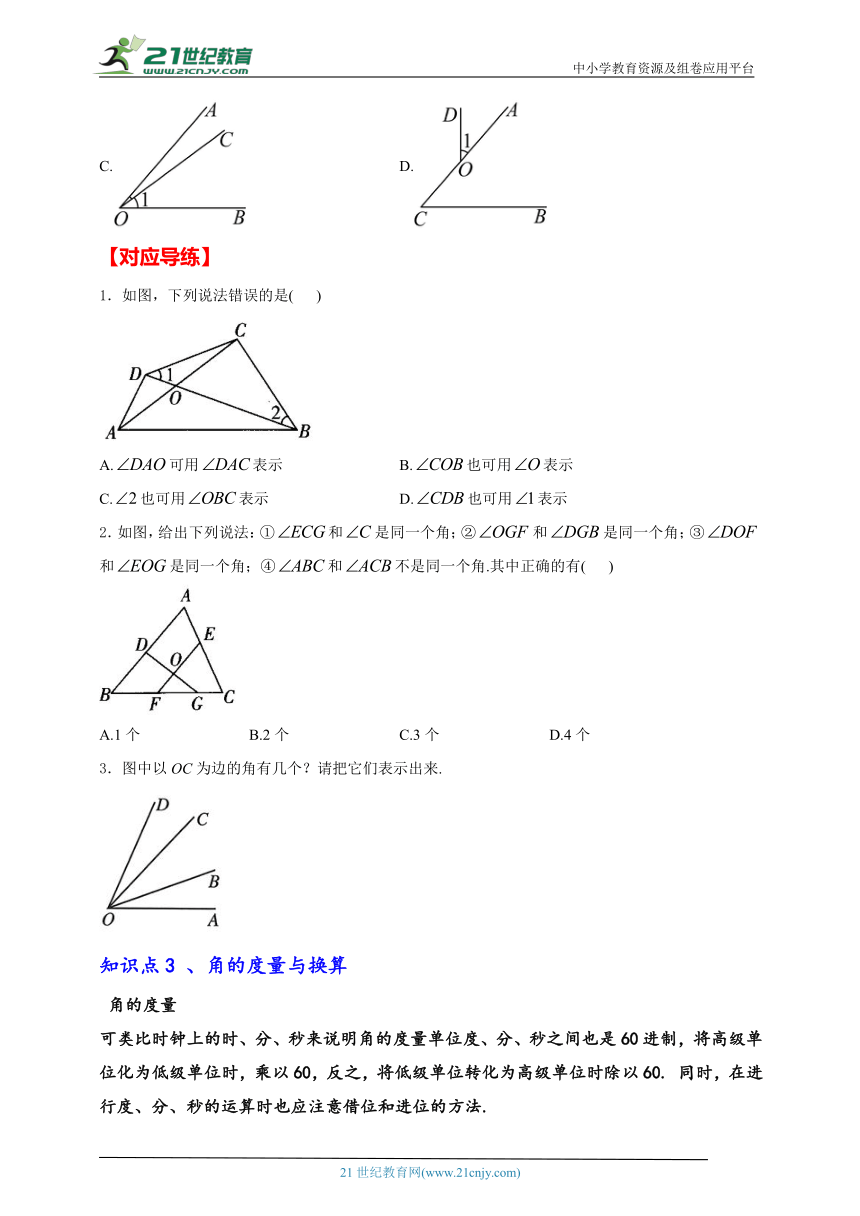
1.如图,下列说法错误的是( )
A.可用表示 B.也可用表示
C.也可用表示 D.也可用表示
2.如图,给出下列说法:①和是同一个角;②和是同一个角;③和是同一个角;④和不是同一个角.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.图中以OC为边的角有几个?请把它们表示出来.
知识点3 、角的度量与换算
角的度量
可类比时钟上的时、分、秒来说明角的度量单位度、分、秒之间也是60进制,将高级单位化为低级单位时,乘以60,反之,将低级单位转化为高级单位时除以60. 同时,在进行度、分、秒的运算时也应注意借位和进位的方法.
1°=60′ ,1′=60″,1周角=360°,1平角=180°
以度分秒为单位的角的度量制,叫做角度制,以弧度为基本度量单位叫弧度制.在军事上常常使用密位制;角的测量工具有: 量角器、经纬仪。
【新知导学】
例3-1.计算:______°______′.
例3-2.比较大小:________.(填“>”“<”或“=”)
【对应导练】
1.把一个平角16等分,则每份(用度、分、秒表示)为_________.
2.将用度、分、秒的形式为( )
A. B. C. D.
3.等于 分,等于 秒,等于 度.
二、题型训练
1.画一个角等于已知角
1.画几个不同的四边形,使每个四边形中都有,,的角.量一量这些四边形中另一个角的度数,你能发现什么规律?
2.同时使用如图所示的一副三角尺能画出哪些角度(小于的角)?至少画出3个表示不同角度的图形,说明理由.
2.角的表示及计数
3.如图,写出:
(1)以C为顶点的所有角;
(2)以AB为一边的所有角;
(3)以F为顶点,FB为一边的所有角.
4.观察图,完成下列问题:
(1)如图①,内部有一条射线,则图中有个角;
(2)如图②,内部有两条射线,,则图中有________个角;
(3)如果内部有10条射线,那么图中有_________个角.
5.根据给出的图形解答下列问题:
(1)表示成,这样的表示方法是否正确?如果不正确,应该怎样改正?
(2)图中哪个角可以用一个大写字母表示?
(3)以A为顶点的角有几个?请表示出来.
(4)与是同一个角吗?请说明理由.
3.角度的换算
6.计算:
(1)把3.38°化为度、分、秒的形式.
(2)把化成度的形式.
7.计算并写出简单的过程:
(1)将用度、分、秒表示;
(2)将用度来表示.
8.填空:
(1)_________°_________'_________";
(2)_________°;
(3)_________'=_________°;
(4)_________'=_________".
4.钟表上的角度问题
9.(1)时钟的时针旋转多少度?
(2)时钟的分针旋转多少度?
(3)3时25分,时钟的时针与分针所成的角是多少度?
.
10.如图,在圆形钟面上,点O为钟面的圆心,以点O为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
(1)在图(1)中画一个锐角,使锐角的内部含有2个数字,且数字之差的绝对值最大;
(2)在图(2)中画一个直角,使直角的内部含有3个数字,且所含3个数字之积等于这3个数字之和;
(3)在图(3)中画一个钝角,使钝角的内部含有4个数字,且数字之和最小;
(4)在图(4)中画一个平角,使平角的内部与外部的数字之和相等;
(5)在图(5)中画两个直角,使这两个直角的内部含有的3个数字之和相等.(画出一种即可)
三、课堂达标
一、单选题(每小题4分,共32分)
1.将用度、分、秒的形式为( )
A. B. C. D.
2.图中角的表示方法正确的有( )
A.1个 B.2个 C.3个 D.4个
3.把化为用度表示的形式,下列正确的是( )
A. B. C. D.
.
4.下列图形中,能用,,三种方法表示同一个角的是( )
A. B.
C. D.
5.下列各角中,是锐角的是( )
A.周角 B.平角 C.平角 D.周角
6.下列说法与如图所示的几何图形相符的是( )
A.点D在线段的延长线上 B.可以表示成
C.射线与射线表示同一条射线 D.
7.时针从上午8时开始沿顺时针方向旋转,此时是( ).
A.9时 B.9时30分 C.10时 D.10时30分
8.如图,下列说法错误的是( )
A.可用表示 B.也可用表示
C.也可用表示 D.也可用表示
二、填空题(每小题4分,共20分)
9.__________°,__________'__________".
11.如图,当7时30分时,时钟上的时针与分针的夹角为__________°.
12.如图,在的内部从O引出3条射线,那么图中共有__________个角;引出5条射线,共有__________个角;引出n条射线,共有__________个角.
13.已知,,则_______(填“>”,“<”或“=”).
三、解答题(每小题4分,共20分)
14.图中以OC为边的角有几个?请把它们表示出来.
15.请将图中的角用不同方法表示出来,并填写下表:
16.已知如图,在同一平面内,有任意四点A、B、C、D.
(1)画出直线,射线,连接;
(2)小红测量,,求的度数;
(3)直接写出图中共有几个角(平角除外).
18.请根据图回答下列问题.
(1)表示成,表示成,表示成,这样的表示方法对不对?如果不对,应该怎样改正?
(2)图中哪个角可以用一个字母来表示?
(3)图中共有几个小于平角的角?请列举出来.
19.如图4-3-1-6
(1)以点B为顶点的角有几个?分别表示出来;
(2)请分别指出以射线BA为边的角;
(3)以D为顶点,DC为一边的小于平角的角有几个?
分别写出来.
新人教版七年级数学上名师点拨与训练
第6章 几何图形
6.3.1 角
学习目标:
1.理解角的两种定义和相关概念,掌握角的表示方法.
2.会正确使用量角器测量角的大小.
3.认识角的单位,会进行度、分、秒之间的换算.
重点:角的两种定义以及三种表示方法.
难点:度、分、秒及其换算.
老师告诉你
角的表示方法
知识点拨
知识点1、角的概念
角的定义:
(1)定义一:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边.如图1所示,角的顶点是点O,边是射线OA、OB.
(2)定义二:一条射线绕着它的端点旋转而形成的图形,射线旋转时经过的平面部分是角的内部.如图2所示,射线OA绕它的端点O旋转到OB的位置时,形成的图形叫做角,起始位置OA是角的始边,终止位置OB是角的终边.
2.注意:
(1)两条射线有公共端点,即角的顶点;角的边是射线;角的大小与角的两边的长短无关.
(2)平角与周角:如图1所示射线OA绕点O旋转,当终止位置OB和起始位置OA成一条直线时,所形成的角叫做平角,如图2所示继续旋转,OB和OA重合时,所形成的角叫做周角.
【新知导学】
例1-1.图中以OC为边的角有几个?请把它们表示出来.
答案:见解析
解析:以OC为边的角有3个,分别为,,.
【对应导练】
1.下列关于角的说法正确的个数是( )
①角是由两条射线组成的图形;②角的边越长,角越大;③在角一边延长线上取一点D;④角可以看作由一条射线绕着它的端点旋转而形成的图形.
A.1 B.2 C.3 D.4
答案:A
解析:角是由两条具有公共端点的射线组成的图形,①错误;
角的大小与边的长短无关,②错误;
角的边是射线,不能延长,③错误.
④角可以看作由一条射线绕着它的端点旋转而形成的图形.,④正确。
故选A
2.下列关于平角、周角的说法正确的是( )
A.平角是一条直线 B.周角是一条射线
C.反向延长射线OA,就形成一个平角 D.两个锐角的和不一定小于平角
答案:C
解析:平角的两边在一直线上,但一条直线构不成平角,A错误
周角的两边在一条射线上,但一条射线构不成周角,B错误
反向延长射线OA构成有公共端点的两条射线,构成角,C正确。
每个锐角都小于90°,它们的和小于180度,小于平角,D错误,
故选C
知识点2 、角的表示
角的几何符号用“∠”表示,角的表示法通常有以下四种:
注意:
用数字或小写希腊字母表示角时,要在靠近角的顶点处加上弧线,且注上阿拉伯数字或小写希腊字母.
【新知导学】
例2-1.下列图形中能用、、三种方法表示同一个角且角表示正确的图形是( )
A. B.
C. D.
答案:B
解析:A.该图可用、表示,不能用表示,故不符合题意;
B.该图可用、表示,不能用表示,故符合题意;
C.该图可用、表示,不能用表示,故不符合题意;
D.该图可用、表示,不能用表示,故不符合题意.
故选B.
例2-2.下列图形中,能用和表示同一个角的是( )
A. B.
C. D.
答案:A
解析:A、因为顶点O处只有一个角,所以这个角能用和,符合题意;
B、因为顶点O处不止一个角,所以这里的所有角均不能用表示,不符合题意;
C、因为顶点O处不止一个角,所以这里的所有角均不能用表示,不符合题意;
D、因为顶点O处不止一个角,所以这里的所有角均不能用表示,不符合题意;
故选A.
【对应导练】
1.如图,下列说法错误的是( )
A.可用表示 B.也可用表示
C.也可用表示 D.也可用表示
答案:B
解析:
2.如图,给出下列说法:①和是同一个角;②和是同一个角;③和是同一个角;④和不是同一个角.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
答案:C
解析:根据角的定义及表示方法,可知①与满足顶点相同,两边所在的射线相同,所以和是同一个角,正确;
②与满足顶点相同,两边所在的射线相同,所以和是同一个角,正确;
③与的顶点相同,两边所在的射线不同,所以和不是同一个角,错误;
④与的顶点不同,两边所在的射线也不同,所以和不是同一个角,正确.
综上,说法正确的有3个.
3.图中以OC为边的角有几个?请把它们表示出来.
答案:见解析
解析:以OC为边的角有3个,分别为,,.
知识点3 、角的度量与换算
角的度量
可类比时钟上的时、分、秒来说明角的度量单位度、分、秒之间也是60进制,将高级单位化为低级单位时,乘以60,反之,将低级单位转化为高级单位时除以60. 同时,在进行度、分、秒的运算时也应注意借位和进位的方法.
1°=60′ ,1′=60″,1周角=360°,1平角=180°
以度分秒为单位的角的度量制,叫做角度制,以弧度为基本度量单位叫弧度制.在军事上常常使用密位制;角的测量工具有: 量角器、经纬仪。
【新知导学】
例3-1.计算:______°______′.
答案:;
解析:
∵
∴
故答案为:;.
例3-2.比较大小:________.(填“>”“<”或“=”)
答案:>
解析:;
故答案为:>.
【对应导练】
1.把一个平角16等分,则每份(用度、分、秒表示)为_________.
答案:
解析:
.因为,
所以,
故答案为.
2.将用度、分、秒的形式为( )
A. B. C. D.
答案:C
解析:,
.
∴.
故选C.
3.等于 分,等于 秒,等于 度.
【解析】解:因为,
所以;
因为,
所以;
因为,
所以;
故答案为:24;75;1.5.
二、题型训练
1.画一个角等于已知角
1.画几个不同的四边形,使每个四边形中都有,,的角.量一量这些四边形中另一个角的度数,你能发现什么规律?
答案:第四个角都是,发现四边形的四个内角和为
解析:图略,通过画出不同的四边形且图中有,,的角,经过测量,这些四边形中第四个角都是,发现四边形的四个内角和为.
2.同时使用如图所示的一副三角尺能画出哪些角度(小于的角)?至少画出3个表示不同角度的图形,说明理由.
答案:、、、、、、、、、、,图见解析,
解析:用三角板画出角,是用角度加减法.比如:画个的角,先将角在纸上画出来,再将角叠加就画出了角.如图:
用一副三角板可以画出:、、、、、、、、、、.
2.角的表示及计数
3.如图,写出:
(1)以C为顶点的所有角;
(2)以AB为一边的所有角;
(3)以F为顶点,FB为一边的所有角.
答案:(1),,,,,
(2),,
(3),,
解析:(1)由图可知:以C为公共端点的射线分别为:射线CB,射线CE,射线CF,射线CD,两两组合可形成:,,,,,;
以C为顶点的角:,,,,,;
(2)如图可知:以射线BA的端点B为公共端点的射线为:射线BF,射线BC,可组成:,;
以射线AB的端点A为公共端点的射线为:射线AD,可组成:,
故以AB为一边的角:,,.
(3)以射线FB的端点F为公共端点的射线为:FA,FC,FD,可组成:,,.
故以F为顶点,FB为一边的角:,,.
4.观察图,完成下列问题:
(1)如图①,内部有一条射线,则图中有个角;
(2)如图②,内部有两条射线,,则图中有________个角;
(3)如果内部有10条射线,那么图中有_________个角.
答案:(1)3
(2)6
(3)66
解析:(1)图①中有,,共3个,
故答案为:3.
(2)在内部画2条射线,,则图中有、、、、、,
共个不同的角;
故答案为:6.
(3)按逆时针方向,以射线为角的始边,
则题图①中分别以射线,为角的终边共有两个角:,;
以射线为始边,射线为终边有一个角:,
所以题图①中角的个数是;
同理,题图②中角的个数是;
经过观察,可以发现角内部射线的条数总比第一个加数小1,
当内部有10条射线时,角的个数是:
.
5.根据给出的图形解答下列问题:
(1)表示成,这样的表示方法是否正确?如果不正确,应该怎样改正?
(2)图中哪个角可以用一个大写字母表示?
(3)以A为顶点的角有几个?请表示出来.
(4)与是同一个角吗?请说明理由.
答案:解:(1)不正确,以A为顶点的角有3个,故不能用表示,可表示为.
(2)题图中可以用一个大写字母表示.
(3)以A为顶点的角有3个,分别是、、.
(4)不是同一个角.理由:这两个角的顶点不同.
解析:
3.角度的换算
6.计算:
(1)把3.38°化为度、分、秒的形式.
(2)把化成度的形式.
答案:解:(1);
(2).
解析:
7.计算并写出简单的过程:
(1)将用度、分、秒表示;
(2)将用度来表示.
答案:(1),
,
所以.
(2),.
.
所以.
解析:
8.填空:
(1)_________°_________'_________";
(2)_________°;
(3)_________'=_________°;
(4)_________'=_________".
答案:(1)8;45;36;
(2)4.23;
(3)600;10;
(4)9;540
解析:
4.钟表上的角度问题
9.(1)时钟的时针旋转多少度?
(2)时钟的分针旋转多少度?
(3)3时25分,时钟的时针与分针所成的角是多少度?
答案:(1)
(2)
(3)
解析:(1)时钟的时针旋转.
(2)时钟的时针旋转.
(3).
10.如图,在圆形钟面上,点O为钟面的圆心,以点O为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
(1)在图(1)中画一个锐角,使锐角的内部含有2个数字,且数字之差的绝对值最大;
(2)在图(2)中画一个直角,使直角的内部含有3个数字,且所含3个数字之积等于这3个数字之和;
(3)在图(3)中画一个钝角,使钝角的内部含有4个数字,且数字之和最小;
(4)在图(4)中画一个平角,使平角的内部与外部的数字之和相等;
(5)在图(5)中画两个直角,使这两个直角的内部含有的3个数字之和相等.(画出一种即可)
答案:(1)见解析
(2)见解析
(3)见解析
(4)见解析
(5)见解析
解析:(1)~(4)如图(1)~图(4)所示.
(5)如图(5)所示,答案不唯一.
三、课堂达标
一、单选题(每小题4分,共32分)
1.将用度、分、秒的形式为( )
A. B. C. D.
答案:C
解析:,
.
∴.
故选C.
2.图中角的表示方法正确的有( )
A.1个 B.2个 C.3个 D.4个
答案:B
解析:题图①应表示为或或;
题图②,是平角,正确;
题图③,射线与周角是两个概念;
题图④可以表示为,正确.
综上所述,正确的有2个.
故选B.
3.把化为用度表示的形式,下列正确的是( )
A. B. C. D.
答案:B
解析:因为,所以,
因为,所以,
所以.
4.下列图形中,能用,,三种方法表示同一个角的是( )
A. B.
C. D.
答案:A
解析:A选项中,可用,,三种方法表示同一个角;
B选项中,能用表示,不能用表示;
C选项中,点A、O、B在一条直线上,
能用表示,不能用表示;
D选项中,能用表示,不能用表示;
故选:A.
5.下列各角中,是锐角的是( )
A.周角 B.平角 C.平角 D.周角
答案:D
解析:周角为,平角为,
所以周角,平角,
周角.
故选D.
6.下列说法与如图所示的几何图形相符的是( )
A.点D在线段的延长线上 B.可以表示成
C.射线与射线表示同一条射线 D.
答案:D
解析:A、点在线段的延长线上,原说法错误,不符合题意;
B、不可以表示成(点C处不止一个角),原说法错误,不符合题意;
C、射线与射线表示不同的射线,原说法错误,不符合题意;
D、,原说法正确,符合题意;
故选:D.
7.时针从上午8时开始沿顺时针方向旋转,此时是( ).
A.9时 B.9时30分 C.10时 D.10时30分
答案:C
解析:由题意得:时针从上午8时开始沿顺时针方向旋转,旋转角为,
时钟一大格一小时是,
,
时钟的时针旋转了两大格即2小时,从上午的8时到上午10时,
故选:C.
8.如图,下列说法错误的是( )
A.可用表示 B.也可用表示
C.也可用表示 D.也可用表示
答案:B
二、填空题(每小题4分,共20分)
9.__________°,__________'__________".
答案:49.5225;21;36
解析:因为,所以.因为,所以,所以.因为,,所以.
10.比较大小:___________(填“>”“<”或“=”).
答案:>
解析:因为,
所以,
故答案为:>.
11.如图,当7时30分时,时钟上的时针与分针的夹角为__________°.
答案:45
解析:
12.如图,在的内部从O引出3条射线,那么图中共有__________个角;引出5条射线,共有__________个角;引出n条射线,共有__________个角.
答案:10;21;
解析:如果引出3条射线,那么题图中共有10个角;引出5条射线,共有21个角;引出n条射线,共有个角.
13.已知,,则_______(填“>”,“<”或“=”).
答案:>
解析:,
,
,
故答案为:>.
三、解答题(每小题4分,共20分)
14.图中以OC为边的角有几个?请把它们表示出来.
答案:见解析
解析:以OC为边的角有3个,分别为,,.
15.请将图中的角用不同方法表示出来,并填写下表:
答案:见解析
解析:(填表略)由题图可知,,(或),(或),.
16.已知如图,在同一平面内,有任意四点A、B、C、D.
(1)画出直线,射线,连接;
(2)小红测量,,求的度数;
(3)直接写出图中共有几个角(平角除外).
答案:(1)见解析
(2)
(3)5
解析:(1)如图,
(2)∵,,
∴;
(3)图中的角有:,,,,,共5个.
17.说出图中共有几个角,并分别写出它们.
答案:逆时针方向数,
以为始边的角有、、 ,
以为始边的角有、,
以为始边的角有,
所以题图中共有个角,
它们分别是,,,,,.
解析:
18.请根据图回答下列问题.
(1)表示成,表示成,表示成,这样的表示方法对不对?如果不对,应该怎样改正?
(2)图中哪个角可以用一个字母来表示?
(3)图中共有几个小于平角的角?请列举出来.
(1)答案:表示方法不对,表示成,表示成,表示成
解析:表示成,表示成,表示成,
这样的表示方法不对,
正确的表示方法为表示成,表示成,表示成.
(2)答案:
解析:图中可以用一个字母表示的角为.
(3)答案:11个,列举见解析
解析:图中小于平角的角有、、、、、、、、、,.
一共有11个角小于平角.
19.如图4-3-1-6
(1)以点B为顶点的角有几个?分别表示出来;
(2)请分别指出以射线BA为边的角;
(3)以D为顶点,DC为一边的小于平角的角有几个?
分别写出来.
答案:(1)以点B为顶点的角有,共3个.
(2)以射线BA为边的角有.
(3)以D为顶点,DC为一边的小于平角的角有,共2个.
解析:
图2
图1
图2
图1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
新人教版七年级数学上名师点拨与训练
第6章 几何图形
6.3.1 角
学习目标:
1.理解角的两种定义和相关概念,掌握角的表示方法.
2.会正确使用量角器测量角的大小.
3.认识角的单位,会进行度、分、秒之间的换算.
重点:角的两种定义以及三种表示方法.
难点:度、分、秒及其换算.
老师告诉你
角的表示方法
知识点拨
知识点1、角的概念
角的定义:
(1)定义一:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边.如图1所示,角的顶点是点O,边是射线OA、OB.
(2)定义二:一条射线绕着它的端点旋转而形成的图形,射线旋转时经过的平面部分是角的内部.如图2所示,射线OA绕它的端点O旋转到OB的位置时,形成的图形叫做角,起始位置OA是角的始边,终止位置OB是角的终边.
2.注意:
(1)两条射线有公共端点,即角的顶点;角的边是射线;角的大小与角的两边的长短无关.
(2)平角与周角:如图1所示射线OA绕点O旋转,当终止位置OB和起始位置OA成一条直线时,所形成的角叫做平角,如图2所示继续旋转,OB和OA重合时,所形成的角叫做周角.
【新知导学】
例1-1.图中以OC为边的角有几个?请把它们表示出来.
【对应导练】
1.下列关于角的说法正确的个数是( )
①角是由两条射线组成的图形;②角的边越长,角越大;③在角一边延长线上取一点D;④角可以看作由一条射线绕着它的端点旋转而形成的图形.
A.1 B.2 C.3 D.4
2.下列关于平角、周角的说法正确的是( )
A.平角是一条直线 B.周角是一条射线
C.反向延长射线OA,就形成一个平角 D.两个锐角的和不一定小于平角
知识点2 、角的表示
角的几何符号用“∠”表示,角的表示法通常有以下四种:
注意:
用数字或小写希腊字母表示角时,要在靠近角的顶点处加上弧线,且注上阿拉伯数字或小写希腊字母.
【新知导学】
例2-1.下列图形中能用、、三种方法表示同一个角且角表示正确的图形是( )
A. B.
C. D.
例2-2.下列图形中,能用和表示同一个角的是( )
A. B.
C. D.
【对应导练】
1.如图,下列说法错误的是( )
A.可用表示 B.也可用表示
C.也可用表示 D.也可用表示
2.如图,给出下列说法:①和是同一个角;②和是同一个角;③和是同一个角;④和不是同一个角.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.图中以OC为边的角有几个?请把它们表示出来.
知识点3 、角的度量与换算
角的度量
可类比时钟上的时、分、秒来说明角的度量单位度、分、秒之间也是60进制,将高级单位化为低级单位时,乘以60,反之,将低级单位转化为高级单位时除以60. 同时,在进行度、分、秒的运算时也应注意借位和进位的方法.
1°=60′ ,1′=60″,1周角=360°,1平角=180°
以度分秒为单位的角的度量制,叫做角度制,以弧度为基本度量单位叫弧度制.在军事上常常使用密位制;角的测量工具有: 量角器、经纬仪。
【新知导学】
例3-1.计算:______°______′.
例3-2.比较大小:________.(填“>”“<”或“=”)
【对应导练】
1.把一个平角16等分,则每份(用度、分、秒表示)为_________.
2.将用度、分、秒的形式为( )
A. B. C. D.
3.等于 分,等于 秒,等于 度.
二、题型训练
1.画一个角等于已知角
1.画几个不同的四边形,使每个四边形中都有,,的角.量一量这些四边形中另一个角的度数,你能发现什么规律?
2.同时使用如图所示的一副三角尺能画出哪些角度(小于的角)?至少画出3个表示不同角度的图形,说明理由.
2.角的表示及计数
3.如图,写出:
(1)以C为顶点的所有角;
(2)以AB为一边的所有角;
(3)以F为顶点,FB为一边的所有角.
4.观察图,完成下列问题:
(1)如图①,内部有一条射线,则图中有个角;
(2)如图②,内部有两条射线,,则图中有________个角;
(3)如果内部有10条射线,那么图中有_________个角.
5.根据给出的图形解答下列问题:
(1)表示成,这样的表示方法是否正确?如果不正确,应该怎样改正?
(2)图中哪个角可以用一个大写字母表示?
(3)以A为顶点的角有几个?请表示出来.
(4)与是同一个角吗?请说明理由.
3.角度的换算
6.计算:
(1)把3.38°化为度、分、秒的形式.
(2)把化成度的形式.
7.计算并写出简单的过程:
(1)将用度、分、秒表示;
(2)将用度来表示.
8.填空:
(1)_________°_________'_________";
(2)_________°;
(3)_________'=_________°;
(4)_________'=_________".
4.钟表上的角度问题
9.(1)时钟的时针旋转多少度?
(2)时钟的分针旋转多少度?
(3)3时25分,时钟的时针与分针所成的角是多少度?
.
10.如图,在圆形钟面上,点O为钟面的圆心,以点O为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
(1)在图(1)中画一个锐角,使锐角的内部含有2个数字,且数字之差的绝对值最大;
(2)在图(2)中画一个直角,使直角的内部含有3个数字,且所含3个数字之积等于这3个数字之和;
(3)在图(3)中画一个钝角,使钝角的内部含有4个数字,且数字之和最小;
(4)在图(4)中画一个平角,使平角的内部与外部的数字之和相等;
(5)在图(5)中画两个直角,使这两个直角的内部含有的3个数字之和相等.(画出一种即可)
三、课堂达标
一、单选题(每小题4分,共32分)
1.将用度、分、秒的形式为( )
A. B. C. D.
2.图中角的表示方法正确的有( )
A.1个 B.2个 C.3个 D.4个
3.把化为用度表示的形式,下列正确的是( )
A. B. C. D.
.
4.下列图形中,能用,,三种方法表示同一个角的是( )
A. B.
C. D.
5.下列各角中,是锐角的是( )
A.周角 B.平角 C.平角 D.周角
6.下列说法与如图所示的几何图形相符的是( )
A.点D在线段的延长线上 B.可以表示成
C.射线与射线表示同一条射线 D.
7.时针从上午8时开始沿顺时针方向旋转,此时是( ).
A.9时 B.9时30分 C.10时 D.10时30分
8.如图,下列说法错误的是( )
A.可用表示 B.也可用表示
C.也可用表示 D.也可用表示
二、填空题(每小题4分,共20分)
9.__________°,__________'__________".
11.如图,当7时30分时,时钟上的时针与分针的夹角为__________°.
12.如图,在的内部从O引出3条射线,那么图中共有__________个角;引出5条射线,共有__________个角;引出n条射线,共有__________个角.
13.已知,,则_______(填“>”,“<”或“=”).
三、解答题(每小题4分,共20分)
14.图中以OC为边的角有几个?请把它们表示出来.
15.请将图中的角用不同方法表示出来,并填写下表:
16.已知如图,在同一平面内,有任意四点A、B、C、D.
(1)画出直线,射线,连接;
(2)小红测量,,求的度数;
(3)直接写出图中共有几个角(平角除外).
18.请根据图回答下列问题.
(1)表示成,表示成,表示成,这样的表示方法对不对?如果不对,应该怎样改正?
(2)图中哪个角可以用一个字母来表示?
(3)图中共有几个小于平角的角?请列举出来.
19.如图4-3-1-6
(1)以点B为顶点的角有几个?分别表示出来;
(2)请分别指出以射线BA为边的角;
(3)以D为顶点,DC为一边的小于平角的角有几个?
分别写出来.
新人教版七年级数学上名师点拨与训练
第6章 几何图形
6.3.1 角
学习目标:
1.理解角的两种定义和相关概念,掌握角的表示方法.
2.会正确使用量角器测量角的大小.
3.认识角的单位,会进行度、分、秒之间的换算.
重点:角的两种定义以及三种表示方法.
难点:度、分、秒及其换算.
老师告诉你
角的表示方法
知识点拨
知识点1、角的概念
角的定义:
(1)定义一:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边.如图1所示,角的顶点是点O,边是射线OA、OB.
(2)定义二:一条射线绕着它的端点旋转而形成的图形,射线旋转时经过的平面部分是角的内部.如图2所示,射线OA绕它的端点O旋转到OB的位置时,形成的图形叫做角,起始位置OA是角的始边,终止位置OB是角的终边.
2.注意:
(1)两条射线有公共端点,即角的顶点;角的边是射线;角的大小与角的两边的长短无关.
(2)平角与周角:如图1所示射线OA绕点O旋转,当终止位置OB和起始位置OA成一条直线时,所形成的角叫做平角,如图2所示继续旋转,OB和OA重合时,所形成的角叫做周角.
【新知导学】
例1-1.图中以OC为边的角有几个?请把它们表示出来.
答案:见解析
解析:以OC为边的角有3个,分别为,,.
【对应导练】
1.下列关于角的说法正确的个数是( )
①角是由两条射线组成的图形;②角的边越长,角越大;③在角一边延长线上取一点D;④角可以看作由一条射线绕着它的端点旋转而形成的图形.
A.1 B.2 C.3 D.4
答案:A
解析:角是由两条具有公共端点的射线组成的图形,①错误;
角的大小与边的长短无关,②错误;
角的边是射线,不能延长,③错误.
④角可以看作由一条射线绕着它的端点旋转而形成的图形.,④正确。
故选A
2.下列关于平角、周角的说法正确的是( )
A.平角是一条直线 B.周角是一条射线
C.反向延长射线OA,就形成一个平角 D.两个锐角的和不一定小于平角
答案:C
解析:平角的两边在一直线上,但一条直线构不成平角,A错误
周角的两边在一条射线上,但一条射线构不成周角,B错误
反向延长射线OA构成有公共端点的两条射线,构成角,C正确。
每个锐角都小于90°,它们的和小于180度,小于平角,D错误,
故选C
知识点2 、角的表示
角的几何符号用“∠”表示,角的表示法通常有以下四种:
注意:
用数字或小写希腊字母表示角时,要在靠近角的顶点处加上弧线,且注上阿拉伯数字或小写希腊字母.
【新知导学】
例2-1.下列图形中能用、、三种方法表示同一个角且角表示正确的图形是( )
A. B.
C. D.
答案:B
解析:A.该图可用、表示,不能用表示,故不符合题意;
B.该图可用、表示,不能用表示,故符合题意;
C.该图可用、表示,不能用表示,故不符合题意;
D.该图可用、表示,不能用表示,故不符合题意.
故选B.
例2-2.下列图形中,能用和表示同一个角的是( )
A. B.
C. D.
答案:A
解析:A、因为顶点O处只有一个角,所以这个角能用和,符合题意;
B、因为顶点O处不止一个角,所以这里的所有角均不能用表示,不符合题意;
C、因为顶点O处不止一个角,所以这里的所有角均不能用表示,不符合题意;
D、因为顶点O处不止一个角,所以这里的所有角均不能用表示,不符合题意;
故选A.
【对应导练】
1.如图,下列说法错误的是( )
A.可用表示 B.也可用表示
C.也可用表示 D.也可用表示
答案:B
解析:
2.如图,给出下列说法:①和是同一个角;②和是同一个角;③和是同一个角;④和不是同一个角.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
答案:C
解析:根据角的定义及表示方法,可知①与满足顶点相同,两边所在的射线相同,所以和是同一个角,正确;
②与满足顶点相同,两边所在的射线相同,所以和是同一个角,正确;
③与的顶点相同,两边所在的射线不同,所以和不是同一个角,错误;
④与的顶点不同,两边所在的射线也不同,所以和不是同一个角,正确.
综上,说法正确的有3个.
3.图中以OC为边的角有几个?请把它们表示出来.
答案:见解析
解析:以OC为边的角有3个,分别为,,.
知识点3 、角的度量与换算
角的度量
可类比时钟上的时、分、秒来说明角的度量单位度、分、秒之间也是60进制,将高级单位化为低级单位时,乘以60,反之,将低级单位转化为高级单位时除以60. 同时,在进行度、分、秒的运算时也应注意借位和进位的方法.
1°=60′ ,1′=60″,1周角=360°,1平角=180°
以度分秒为单位的角的度量制,叫做角度制,以弧度为基本度量单位叫弧度制.在军事上常常使用密位制;角的测量工具有: 量角器、经纬仪。
【新知导学】
例3-1.计算:______°______′.
答案:;
解析:
∵
∴
故答案为:;.
例3-2.比较大小:________.(填“>”“<”或“=”)
答案:>
解析:;
故答案为:>.
【对应导练】
1.把一个平角16等分,则每份(用度、分、秒表示)为_________.
答案:
解析:
.因为,
所以,
故答案为.
2.将用度、分、秒的形式为( )
A. B. C. D.
答案:C
解析:,
.
∴.
故选C.
3.等于 分,等于 秒,等于 度.
【解析】解:因为,
所以;
因为,
所以;
因为,
所以;
故答案为:24;75;1.5.
二、题型训练
1.画一个角等于已知角
1.画几个不同的四边形,使每个四边形中都有,,的角.量一量这些四边形中另一个角的度数,你能发现什么规律?
答案:第四个角都是,发现四边形的四个内角和为
解析:图略,通过画出不同的四边形且图中有,,的角,经过测量,这些四边形中第四个角都是,发现四边形的四个内角和为.
2.同时使用如图所示的一副三角尺能画出哪些角度(小于的角)?至少画出3个表示不同角度的图形,说明理由.
答案:、、、、、、、、、、,图见解析,
解析:用三角板画出角,是用角度加减法.比如:画个的角,先将角在纸上画出来,再将角叠加就画出了角.如图:
用一副三角板可以画出:、、、、、、、、、、.
2.角的表示及计数
3.如图,写出:
(1)以C为顶点的所有角;
(2)以AB为一边的所有角;
(3)以F为顶点,FB为一边的所有角.
答案:(1),,,,,
(2),,
(3),,
解析:(1)由图可知:以C为公共端点的射线分别为:射线CB,射线CE,射线CF,射线CD,两两组合可形成:,,,,,;
以C为顶点的角:,,,,,;
(2)如图可知:以射线BA的端点B为公共端点的射线为:射线BF,射线BC,可组成:,;
以射线AB的端点A为公共端点的射线为:射线AD,可组成:,
故以AB为一边的角:,,.
(3)以射线FB的端点F为公共端点的射线为:FA,FC,FD,可组成:,,.
故以F为顶点,FB为一边的角:,,.
4.观察图,完成下列问题:
(1)如图①,内部有一条射线,则图中有个角;
(2)如图②,内部有两条射线,,则图中有________个角;
(3)如果内部有10条射线,那么图中有_________个角.
答案:(1)3
(2)6
(3)66
解析:(1)图①中有,,共3个,
故答案为:3.
(2)在内部画2条射线,,则图中有、、、、、,
共个不同的角;
故答案为:6.
(3)按逆时针方向,以射线为角的始边,
则题图①中分别以射线,为角的终边共有两个角:,;
以射线为始边,射线为终边有一个角:,
所以题图①中角的个数是;
同理,题图②中角的个数是;
经过观察,可以发现角内部射线的条数总比第一个加数小1,
当内部有10条射线时,角的个数是:
.
5.根据给出的图形解答下列问题:
(1)表示成,这样的表示方法是否正确?如果不正确,应该怎样改正?
(2)图中哪个角可以用一个大写字母表示?
(3)以A为顶点的角有几个?请表示出来.
(4)与是同一个角吗?请说明理由.
答案:解:(1)不正确,以A为顶点的角有3个,故不能用表示,可表示为.
(2)题图中可以用一个大写字母表示.
(3)以A为顶点的角有3个,分别是、、.
(4)不是同一个角.理由:这两个角的顶点不同.
解析:
3.角度的换算
6.计算:
(1)把3.38°化为度、分、秒的形式.
(2)把化成度的形式.
答案:解:(1);
(2).
解析:
7.计算并写出简单的过程:
(1)将用度、分、秒表示;
(2)将用度来表示.
答案:(1),
,
所以.
(2),.
.
所以.
解析:
8.填空:
(1)_________°_________'_________";
(2)_________°;
(3)_________'=_________°;
(4)_________'=_________".
答案:(1)8;45;36;
(2)4.23;
(3)600;10;
(4)9;540
解析:
4.钟表上的角度问题
9.(1)时钟的时针旋转多少度?
(2)时钟的分针旋转多少度?
(3)3时25分,时钟的时针与分针所成的角是多少度?
答案:(1)
(2)
(3)
解析:(1)时钟的时针旋转.
(2)时钟的时针旋转.
(3).
10.如图,在圆形钟面上,点O为钟面的圆心,以点O为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
(1)在图(1)中画一个锐角,使锐角的内部含有2个数字,且数字之差的绝对值最大;
(2)在图(2)中画一个直角,使直角的内部含有3个数字,且所含3个数字之积等于这3个数字之和;
(3)在图(3)中画一个钝角,使钝角的内部含有4个数字,且数字之和最小;
(4)在图(4)中画一个平角,使平角的内部与外部的数字之和相等;
(5)在图(5)中画两个直角,使这两个直角的内部含有的3个数字之和相等.(画出一种即可)
答案:(1)见解析
(2)见解析
(3)见解析
(4)见解析
(5)见解析
解析:(1)~(4)如图(1)~图(4)所示.
(5)如图(5)所示,答案不唯一.
三、课堂达标
一、单选题(每小题4分,共32分)
1.将用度、分、秒的形式为( )
A. B. C. D.
答案:C
解析:,
.
∴.
故选C.
2.图中角的表示方法正确的有( )
A.1个 B.2个 C.3个 D.4个
答案:B
解析:题图①应表示为或或;
题图②,是平角,正确;
题图③,射线与周角是两个概念;
题图④可以表示为,正确.
综上所述,正确的有2个.
故选B.
3.把化为用度表示的形式,下列正确的是( )
A. B. C. D.
答案:B
解析:因为,所以,
因为,所以,
所以.
4.下列图形中,能用,,三种方法表示同一个角的是( )
A. B.
C. D.
答案:A
解析:A选项中,可用,,三种方法表示同一个角;
B选项中,能用表示,不能用表示;
C选项中,点A、O、B在一条直线上,
能用表示,不能用表示;
D选项中,能用表示,不能用表示;
故选:A.
5.下列各角中,是锐角的是( )
A.周角 B.平角 C.平角 D.周角
答案:D
解析:周角为,平角为,
所以周角,平角,
周角.
故选D.
6.下列说法与如图所示的几何图形相符的是( )
A.点D在线段的延长线上 B.可以表示成
C.射线与射线表示同一条射线 D.
答案:D
解析:A、点在线段的延长线上,原说法错误,不符合题意;
B、不可以表示成(点C处不止一个角),原说法错误,不符合题意;
C、射线与射线表示不同的射线,原说法错误,不符合题意;
D、,原说法正确,符合题意;
故选:D.
7.时针从上午8时开始沿顺时针方向旋转,此时是( ).
A.9时 B.9时30分 C.10时 D.10时30分
答案:C
解析:由题意得:时针从上午8时开始沿顺时针方向旋转,旋转角为,
时钟一大格一小时是,
,
时钟的时针旋转了两大格即2小时,从上午的8时到上午10时,
故选:C.
8.如图,下列说法错误的是( )
A.可用表示 B.也可用表示
C.也可用表示 D.也可用表示
答案:B
二、填空题(每小题4分,共20分)
9.__________°,__________'__________".
答案:49.5225;21;36
解析:因为,所以.因为,所以,所以.因为,,所以.
10.比较大小:___________(填“>”“<”或“=”).
答案:>
解析:因为,
所以,
故答案为:>.
11.如图,当7时30分时,时钟上的时针与分针的夹角为__________°.
答案:45
解析:
12.如图,在的内部从O引出3条射线,那么图中共有__________个角;引出5条射线,共有__________个角;引出n条射线,共有__________个角.
答案:10;21;
解析:如果引出3条射线,那么题图中共有10个角;引出5条射线,共有21个角;引出n条射线,共有个角.
13.已知,,则_______(填“>”,“<”或“=”).
答案:>
解析:,
,
,
故答案为:>.
三、解答题(每小题4分,共20分)
14.图中以OC为边的角有几个?请把它们表示出来.
答案:见解析
解析:以OC为边的角有3个,分别为,,.
15.请将图中的角用不同方法表示出来,并填写下表:
答案:见解析
解析:(填表略)由题图可知,,(或),(或),.
16.已知如图,在同一平面内,有任意四点A、B、C、D.
(1)画出直线,射线,连接;
(2)小红测量,,求的度数;
(3)直接写出图中共有几个角(平角除外).
答案:(1)见解析
(2)
(3)5
解析:(1)如图,
(2)∵,,
∴;
(3)图中的角有:,,,,,共5个.
17.说出图中共有几个角,并分别写出它们.
答案:逆时针方向数,
以为始边的角有、、 ,
以为始边的角有、,
以为始边的角有,
所以题图中共有个角,
它们分别是,,,,,.
解析:
18.请根据图回答下列问题.
(1)表示成,表示成,表示成,这样的表示方法对不对?如果不对,应该怎样改正?
(2)图中哪个角可以用一个字母来表示?
(3)图中共有几个小于平角的角?请列举出来.
(1)答案:表示方法不对,表示成,表示成,表示成
解析:表示成,表示成,表示成,
这样的表示方法不对,
正确的表示方法为表示成,表示成,表示成.
(2)答案:
解析:图中可以用一个字母表示的角为.
(3)答案:11个,列举见解析
解析:图中小于平角的角有、、、、、、、、、,.
一共有11个角小于平角.
19.如图4-3-1-6
(1)以点B为顶点的角有几个?分别表示出来;
(2)请分别指出以射线BA为边的角;
(3)以D为顶点,DC为一边的小于平角的角有几个?
分别写出来.
答案:(1)以点B为顶点的角有,共3个.
(2)以射线BA为边的角有.
(3)以D为顶点,DC为一边的小于平角的角有,共2个.
解析:
图2
图1
图2
图1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
